Physical Mechanisms of Cancer in the Transition to Metastasis

Abstract

Whether a tumor is metastatic is one of the most significant factors that influence the prognosis for a cancer patient. The transition from a nonmetastatic tumor to a metastatic one is accompanied by a number of genetic and proteomic changes within the tumor cells. These protein-level changes conspire to produce behavioral changes in the cells: cells that had been relatively stationary begin to move, often as a group. In this study we ask the question of what cell-level biophysical changes are sufficient to initiate evasion away from an otherwise static tumor. We use a mathematical model developed to describe the biophysics of epithelial tissue to explore this problem. The model is first validated against in vitro wound healing experiments with cancer cell lines. Then we simulate the behavior of a group of mutated cells within a sea of healthy tissue. We find that moderate increases in adhesion between the cell and extracellular matrix (ECM) accompanied by a decrease in cell-cell adhesion and/or Rho family of small GTPase activation can cause a group of cells to break free from a tumor and spontaneously migrate. This result may explain why some metastatic cells have been observed to upregulate integrin, downregulate cadherin, and activate Rho family signaling.

Introduction

The prototypical progression of cancer involves sequential genetic mutations that alter cell cycle control and many other cellular functions (1). In this paradigmatic picture, the primary tumor begins as a small, noninvasive growth where dysregulation of cell replication and death leads to expansion of the tumor mass. As the tumor continues to grow, further genetic mutations cause some cells to become more invasive, possibly because of altered cell-cell and cell-ECM interactions (2, 3, 4). Eventually, certain cells metastasize, breaking free from the primary tumor and migrating to distal parts of the body. Some of these cells may settle in a new location in the body and form a secondary tumor. Approximately 90% of cancer fatalities are attributable to these secondary tumors that result from metastasis (5, 6).

Metastasis is usually the main factor in determining a patient’s prognosis (1), and many cancer drugs are developed to inhibit metastatic invasion of tumors (7). However, metastasis does not evolve through a specific program of mutations, as is suggested by the prototypical progression. A major stumbling block in cancer treatment is that genotypic and proteomic variation in metastatic cells is largely heterogeneous (8, 9), which suggests that metastatic potential is not dictated by specific mutations but, rather, can be achieved in a large number of different ways. The resulting metastatic cells, though, have similar behavior at the functional level: they migrate away from the site of the primary tumor, moving through tissues and into and out of the bloodstream. Because metastasis is an inherently physical process, we propose that the heterogeneous genetic and molecular-level changes that occur during the transition to metastasis conspire to produce specific biophysical changes inside the cell that define metastatic potential. Indeed, the biomechanics and biophysics of cells are known to be altered in cancer (10), including changes in cell stiffness, adhesion, and traction forces (11, 12, 13), and two distinct processes that have been implicated in the transition to metastasis, epithelial-to-mesenchymal transitions (EMT) or mutations in suppressor genes (MSGs), such as p53, both lead to alterations in cell-cell adhesion and activation of Rho GTPases (14, 15, 16). We, therefore, pose the question of what cell-level biophysical alterations can produce metastasis.

In this study we begin to address this question using mathematical modeling and examine the early stages of the transition to metastasis: the initial evasion away from the primary tumor. Most cancers originate in epithelial tissues (1). Our group recently developed a model that accurately describes the physics and motion of cells within epithelial layers during wound healing assays (17, 18). This model considers four major factors of epithelial biophysics: cell polarity, actomyosin contractility, cell-cell adhesion, and cell-ECM adhesion (Fig. 1). It is possible that any or all of these processes are modified during metastatic transition. To show that our model is relevant for cancer metastasis, we begin our investigation by first validating the model against results from a number of wound healing experiments reported in the literature that probed how alterations in cell-cell adhesion and actomyosin contractility affect cancer cell migration rates. We then develop the model within the context of a simplified picture of a tumor and show that localized modifications of cellular biophysics can drive spontaneous migration of cell clusters. The biophysical alterations that we identify to be necessary for evasion away from the initial tumor are consistent with these previous reports on the effect of specific proteins on metastatic potential and provide new insight, to our knowledge, into what factors influence metastasis.

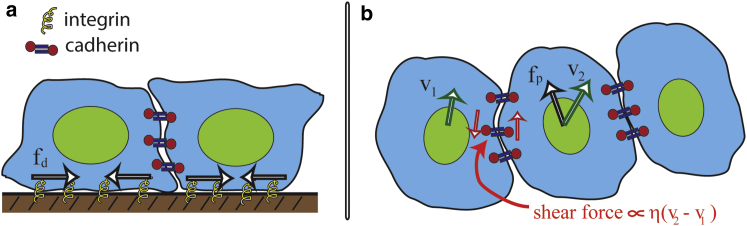
Figure 1.

Schematic of the principal features of our model for collective cellular migration. Our model considers four principle forces: a propulsive force due to the interaction between actin and the substrate via integrin molecules; resistance to the motion of the cell from the substrate, also mediated by integrin; a dipole-distributed stress produced by intracellular contraction; and cell-cell adhesion forces. (a) A lateral view is shown of two cells on a substrate highlights adhesion to the substrate through integrin molecules, and how cytoskeletal flows inside the cell transmit the dipole distributed stress to the substrate denoted by f_d. The cells are attached to each other through cadherin bonds. (b) A top-down view is shown of three cells in contact highlights the protrusive force f_p that is exerted onto the substrate (black arrow). This force depends on integrin and the intracellular actin flow and is assumed to be directed along the polarization direction of the cell. Differences in the velocities between neighboring cells cause shear forces on the cadherin molecules, which leads to an effective viscous shear stress in the tissue. v₁ and v₂ (green arrows) denote the velocities of the left and center cells, respectively. The magnitude of the shear stress is proportional to an effective viscosity, which is denoted by η, and the difference in velocity between the cells. Our model averages these forces over a small region of cells to produce a continuum description for the epithelial layer (see Supporting Material). To see this figure in color, go online.

Materials and Methods

Mathematical model

A complete description of the mathematical model and the method that we used to solve the equations is given in the Supporting Material. Here, we give a brief description of the equations and the numerical method.

Force balance in the monolayer

Epithelia can be treated as a continuous sheet of cells that is in contact with a rigid surface (such as a basement membrane) (17). Because the resistance from the environment is much larger than inertia, the sum of the forces is equal to zero. We assume that there are four forces that act within the cell layer: 1) individual cells produce a local propulsive force of magnitude f_p that is directed along the cell polarization d; 2) movement of the cells across the surface (e.g., basement membrane) is resisted by a drag force proportional to the local velocity v, with drag coefficient ζ; 3) intracellular processes produce a contractile stress that is aligned along the direction of the cell polarization, with the stress given by f_ddd; and 4) cell-cell adhesion leads to an additional stress σ_m that acts between the cells. The force balance equation is then as follows (see the Supporting Material):

$$\nabla \cdot {\sigma }_m=\zeta \mathbf{v}+\nabla \cdot \left({\mathit{f}}_d\mathbf{d}\mathbf{d}\right)-{\mathit{f}}_p\mathbf{d}.$$ (1)

Dynamics of cell density

The cell density $c$ is governed by the continuity equation:

$$\frac{\partial c}{\partial t}+\nabla \cdot \left(\mathbf{v}c\right)=D{\nabla }^{2}c,$$ (2)

where the cells migrate with a local velocity v and we allow for diffusion with coefficient $D$.

Dynamics of the polarization direction

Motile cells are polarized: they move in a specific direction. The cell polarization is represented by the vector d. This polarization field moves and rotates because of the motion of the cells. Because the cells adhere to the substrate, there is resistance to the rotation of the cells, which is proportional to the rotational rate, with a rotational drag coefficient ζ_r. This drag coefficient is related to the cell-substrate drag coefficient ζ_r = ζL²/12, where L is the diameter of the cell. In addition, we assume that there is a tendency for nearby cells to align with one another, the strength of which is governed by a Frank constant K. This tendency to align can be attributed to two factors. First, individual cells have a uniform polarization. Therefore, in our continuum description the polarization vector should not change on length scales smaller than the size of the cell. Second, steric interactions between cells and/or cell signaling could act to orient neighboring cells, which would increase the distance over which there is a tendency for the cells to remain aligned. The Frank constant divided by the rotational drag coefficient acts like a diffusion coefficient and has units of velocity times length. We can then estimate the value of K/ζ_r using the average velocity of a cell (∼10 μm/h) times the length scale over which the polarization should be roughly constant (∼10 μm). Therefore, K/ζ_r ∼100 μm/h². Under these assumptions, the overall dynamics of the cell polarization obeys a similar equation to the dynamics of the director field in nematic liquid crystals (14):

$${\zeta }_r\left(\frac{\partial \mathsf{d}}{\partial t}+\mathbf{v}\cdot \nabla \mathbf{d}-\frac{1}{2}\left(\nabla \times \mathbf{v}\right)\times \mathbf{d}\right)=K{\nabla }^2\mathbf{d}.$$ (3)

This equation represents the balance between the orientational drag on the left-hand side, and the elastic torque from polarized cells at the right-hand side.

The cell-cell adhesion stress

We have previously shown (17) that because cell-cell adhesion is primarily mediated by cadherin bonds that have turnover times on the scale of 15 min to 1 h (19), that the cell-cell interaction stress can be modeled as a Maxwell fluid. We therefore use this description to define the dynamic equation for σ_m (see the Supporting Material):

$$\begin{array}{c}\tau \frac{\partial {\sigma }_m}{\partial t}+{\sigma }_m=\eta \left(\nabla \mathsf{v}+{\left(\nabla \mathsf{v}\right)}^T\right)+\left(\lambda -\eta \right)\left(\nabla \cdot \mathsf{v}\right)\mathbf{I}-{\sigma }_0\left(c-c_0\right)\mathbf{I}\\ -\beta \left(\frac{V_{\text{tumor}}^0-V_{\text{tumor}}}{V_{\text{tumor}}^0}\right){\mathbf{I}}_{\text{tumor}}.\end{array}$$ (4)

In this model, τ is te cadherin turnover timescale, and η is a cell-cell viscosity that depends on the average number of bound cadherin molecules and the strength of the cadherin bond. In addition, there is resistance to compression or extension that is defined by two parameters. First, because cells in monolayers extend lamellipodia under other cells (20), we assume that there are viscous forces that resist compression or extension with a strength proportional to the volumetric viscosity λ. Second, because the cells themselves are elastic, there is an effective pressure that tries to preserve cell density that is proportional to the bulk modulus σ₀. The identity matrix is defined as I. For our monolayer tumor model, we also add in an additional pressure to preserve the area of mutated region. The strength of this term is given by β and this term is only used within the tumor region.

Numerical methods

The two-dimensional (2D) free boundary problem was solved using the moving boundary node method (19). This method is a level set-based, finite volume algorithm. For these simulations, we used a time step of 0.001 h and a grid spacing that was 1/40 of the initial width of the domain (i.e., for a monolayer with an initial width of 250 μm, the grid spacing was 7.5 μm). Because of the initial random orientations in the cellular migration, we collect 20 simulations for averaging the migration velocity. For more information on our numerical discretization see the Supporting Material.

Results

When a single epithelial cell is plated onto a substrate, it crawls, moving along a given direction over tens of minutes and randomly reorienting on longer timescales (21). Inside the cell, the actin cytoskeleton flows rearward at the front of the cell and forward at the rear, driven by polymerization and actomyosin contraction (22). This cytoskeletal flow, through its interaction with adhesion proteins, such as integrin, exerts traction stresses on the substrate that are in the same direction as the flow (23). To a first approximation, then, the traction forces have a dipole distribution that is aligned with the cell motion. In addition, when the same cell is in contact with other cells, it adheres to the neighboring cells via cadherin molecules (24, 25), and cell movements can compress or stretch the cells. Therefore, we can break the forces that act on a cell in a monolayer into four primary components: a propulsive force that pushes the cell along the surface f_p, a resistive force from the substrate that is proportional to the velocity with drag coefficient ζ, a dipole-distributed stress from the cytoskeletal flow f_d, and forces due to cell-cell adhesion (Fig. 1). In addition, there is an isotropic pressure due to cell elasticity that maintains the cell density. We have previously shown that forces due to cell-cell adhesion produce a viscoelastic stress within the epithelial layer that depends on the cadherin turnover time τ and an effective viscosity η (17) (Fig. 1). Because resistive forces are large compared with the cells’ inertia, the sum of the forces on any cell is zero. Therefore, averaging over the forces on a cell leads to a continuum-level force balance equation that defines the velocity field within the epithelium. This model has been previously shown to reproduce the complex dynamics that are observed during Madin-Darby canine kidney (MDCK) wound healing experiments (the detailed mathematical model is given in the Supporting Material, and the model parameters are shown in Table 1) (17, 18, 26, 27). The force balance description that we use contains many of the same features that have been used in discrete cell models for collective migration (28, 29, 30); however, our model also includes intracellular contraction, which is often ignored in these models, with one notable exception that included membrane contraction (30). Although our model was developed to describe wound healing experiments, the biophysical features of cell motility and cell-cell interactions that are included in the model are broadly applicable to epithelial, cancer, and many other motile cell types and are not specific to only wound healing scenarios. Therefore, it is reasonable to assume that the same model may also be informative about cancer cell migration and the transition to metastasis.

Table 1.

Model Parameters

Parameter	Symbol	Value	Source
Viscoelastic timescale	τ	0.25 h	E.E (25), C2 cells
Effective shear viscosity	η	10 dynes × h/cm	E.S.
Volumetric viscosity	λ	103 dynes × h/cm	E.S.
Substrate drag coefficient	ζ	2.5 × 104 dynes × h/cm3	E.E (23, 55), MDCK, MEF
Average cell crawling speed	V0	10 μm/h	(55), MEF
Propulsive force	fp = ζ V0	25 dynes/cm2	E.E (23, 55), MDCK
Traction stress	fd	∼103 dynes/cm	(23), MDCK
Dipole length	b	10 μm	E.E (23), MDCK
Rotational drag coefficient	ζr	400 dynes × h/cm2	E.E (56), 3T3
Frank constant	K	2 × 10−4 dynes	E.E (26), MDCK

E.S. (estimated from simulations) is the value determined by matching simulation results to existing experimental data; E.E. (estimated from experiments). The following cell types were used to determine these parameters: Madin-Darby canine kidney (MDCK), mouse embryonic fibroblasts (MEF), Swiss 3T3 fibroblasts (3T3), and Mouse C2 cells (C2).

Validation of the model for cancer cells

Because our collective migration model has only been validated against MDCK experiments, it is important to first determine that it can reproduce behaviors in cancer-relevant cell types before embarking on modeling metastasis. In addition, it is also important to test that the model provides realistic predictions when the migrating cells are biophysically perturbed in a way that alters the model parameters. To this end, we chose to compare our simulations from data from two representative wound healing experiments.

Effects of cell-cell adhesion on the rate of wound healing

The first experiment examined the role of cadherin (cell-cell adhesion) on MCF10A migration, a breast-derived epithelial cell line that is often used in cancer biology studies (31). This experiment examined the effects of transforming growth factor β1 (TGF-β1) on EMT, a key transition in metastatic transformation (32). In EMT, E-cadherin is downregulated, whereas N-cadherin is upregulated. In this work, it was shown that N-cadherin knockdown leads to E-cadherin upregulation and vice versa. When N-cadherin was knocked down in these cells, the rate that in vitro wounds healed increased by approximately a factor of 2, but only in the presence of TGF-β1. However, overexpression of N-cadherin (E-cadherin knockdown) increased wound healing rates by a factor of 1.2 in the absence of TGF-β1 (31).

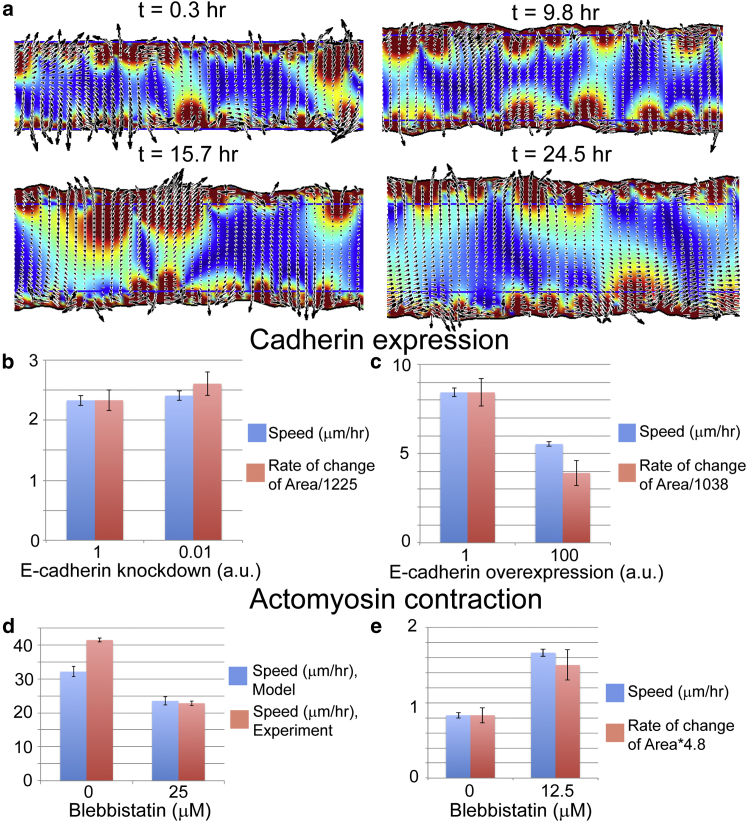
To explore the role of cadherin in wound healing with our model, we used a baseline set of parameters (Table 1) to define the forces and viscosity of MCF10A cells before exposure to TGF-β1. We simulated a strip of cells that is 250 μm wide and 1000 μm long that is bounded by a denuded region on either side of the strip (Fig. 2 a). Boundaries along the width of the cell strip were treated as free boundaries, and periodic boundaries were used along the length. We computed the average velocity of the wound as the cells migrated out into the denuded region. Random initial conditions were used and we ran 10 simulations per condition to determine the average and standard error for the velocity. For the baseline parameters, we found an average border velocity of 2.3 ± 0.1 μm/h, which is slightly slower than what is measured for MDCK wound healing assays (27). Because E-cadherin is the key mediator of cell-cell adhesion (3), we assumed that the cell-cell interaction viscosity depends on E-cadherin levels in a concentration-dependent manner. E-cadherin adhesions involve the dimerization of molecules between cells. Therefore, we expect that the viscosity should scale like the square of the cadherin concentration. To simulate the N-cadherin overexpression experiments, we therefore decreased this viscosity by a factor of 100 to simulate knockdown of E-cadherin by ∼10-fold. We found that decreased cell-cell viscosity produced a roughly 1.1-fold increase in the wound healing rate, which was in agreement with the increase in the time rate of change of the area measure in the experiments (Fig. 2 b) (31). We then simulated TGF-β1 stimulation using an 8-fold increase in the propulsive force f_p and traction stress f_d in the model. This increase leads to an 8-fold change in border advance velocity from the baseline parameters, which matches the increase seen experimentally with TGF-β1 stimulation (31). To simulate N-cadherin knockdown, we increased the cell-cell viscosity by a factor of 100 and found a decrease in border advance of ∼1.6, which compares with the factor of 2 measured experimentally (Fig. 2 c) (31).

Figure 2.

(a) We validated our model by comparing simulations with previous wound healing experiments that perturbed cell-cell adhesion and actomyosin contraction in cancer-relevant cell lines. The wound healing simulations compute the velocity field in a strip of epithelial cells. We track the spreading of a strip of cells and measure the average rate of the border advance. Overexpression of N-cadherin leads to decreased levels of E-cadherin and was shown to produce a small increase in the time rate of change of the area of a wounded layer of MCF10A cells (b, red bars), whereas knockdown of N-cadherin reduced E-cadherin levels and slowed the progression of the area (c, red bars) (data for the time rate of change of the area dA/dt taken from (33) and scaled to compare with simulation velocities). Our model also shows that decreasing the cell-cell adhesion (the cell-cell viscosity η) produces a modest increase in the advance of the border (b, blue bars), whereas increasing cell-cell adhesion slows border advance in our simulations (c, blue bars). (d and e) Blebbistatin treatment differentially affects different cell types. MCF10A cells on rigid substrate migrate rapidly and are slowed down when blebbistatin is used to inhibit actomyosin contraction (34) (d, red bars). Consistent with this finding, our model produces a decrease in speed when we decrease the dipole stress for parameters that give fast migration (d, blue bars). On the other hand, border speed in slower cells, such as hepatic cells, is observed to increase upon blebbistatin treatment (33), which agrees with our model when we use parameters that reduce the overall border migration (e, red bars are data from (33); blue bars are simulation results). See text and Table 1 for parameters and details. To see this figure in color, go online.

Effects of actomyosin contraction on the rate of wound healing

The literature on the role of actomyosin contraction in wound healing is somewhat contradictory. Experiments done with mouse hepatic stellate cells suggests that wound healing assays close faster when myosin-II is inhibited by blebbistatin at doses up to 50 μM (33). Conversely, wound healing assays with MCF10A cells on hard substrates (65 kPa) are slowed by 25 μM blebbistatin treatment, but no significant effect is noticed on soft substrates (3kPa) (34). Similarly, the rate of wound healing in mouse epithelial kidney cells is not affected by blebbistatin treatment (35).

Although the reported effects of blebbistatin seem contradictory, it is important to note that there is marked difference in how fast the wound border edge progresses for each of these cell types. The hepatic cells are the slowest, with an average border advance on order of 15 μm/h (33). The mouse kidney cells and the MCF10As on soft substrates progressed at ∼20–25 μm/h, and the MCF10As on hard substrates moved at ∼42 μm/h (34, 35). Blebbistatin treatment is expected to reduce the contractile stress that cells exert on the substrate. In addition, we hypothesize that the rate of border advance correlates with the propulsive force from the cells, which is consistent with experimental observations of the role of profilin in wound healing (36). Therefore, we used our model to examine how the contractile dipole-distributed stress affects wound healing rates for parameters that give comparable velocities with what is observed in these experiments. To reproduce the velocity of MCF10As on stiff substrates, we set a propulsive force of f_p = 1600 dynes/cm² and a dipole stress of f_d = 500 dynes/cm. A 25 μM blebbistatin treatment was mimicked by reducing the dipole stress to f_d = 6.25 dynes/cm. These simulations gave a velocity of 32 ± 2.7 μm/h for the untreated cells, and blebbistatin treatment resulted in a decreased border speed of 23 ± 2.5 μm/h (Fig. 2 d). These results are in reasonable agreement with the MCF10A border speeds measured on stiff substrates (34). To simulate the slower hepatic cells, we used a propulsive force of f_p = 375 dynes/cm², a dipole stress of f_d = 1500 dynes/cm, and a substrate drag coefficient ζ = 1.25 × 10⁴ dynes h/cm³. Blebbistatin treatment was simulated by reducing the dipole stress to f_d = 500 dynes/cm. The untreated simulation gave a border velocity of 0.82 ± 0.05 μm/h and the blebbistatin simulations produced a larger velocity of 1.66 ± 0.07 μm/h, which was consistent with the observed increase in the number of cells in the wounded region after 24 h (Fig. 2 e) (33).

Cellular biophysics in the initial evasion from the primary tumor

The preceding results suggest that our collective migration model can accurately simulate the collective movements of epithelial cells under alterations that influence force production and cell-cell adhesion. To test our hypothesis that these biophysical parameters are key determinants of early metastasis, we consider a simplified picture of a tumor undergoing a metastatic transition. We treat the main tumor mass as being comprised of biophysically similar, nonmetastatic cells surrounding a group of mutated (i.e., biophysically altered), potentially malignant cells (Fig. 3 a). Because most cancers originate in epithelial tissues (1), our mathematical model that is based on the physics and motion of cells within epithelial layers is appropriate to explore what localized alterations in cellular biophysical parameters will cause the altered population of cells to spontaneously migrate. Because this is a continuum-level model for collective migration, our analysis is most applicable to cancers that involve collective motion during metastasis, such as melanoma, squamous cell carcinoma, large-cell lung cancer, epithelial prostate cancer, lobular breast cancers, and rhabdomyosarcoma (37).

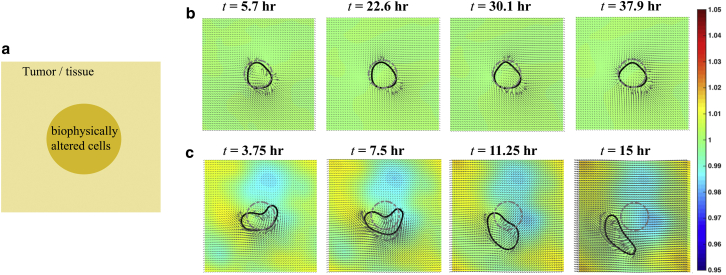
Figure 3.

Mutations can lead to spontaneous migration in confluent cell layers. (a) Schematic of the initial condition of a simplified tumor model is shown. A tissue/tumor of epithelial cells (pale yellow) surrounds a 100 μm diameter region of biophysically altered cells. We examined what biophysical alterations are sufficient to lead to spontaneous migration of these mutated cells. (b) Results from a control simulation (Movie S1). The cells in the initially circular region (dotted gray contour) have the same biophysical parameters as the exterior tissue. The initially circular region deforms some over the course of the simulation, as shown by the black contour, but the center of mass remains within the initial circular region. (c) When the cell-ECM adhesion is increased by a factor of 5 and the cell-cell adhesion is decreased by a factor of 5 (which represents upregulation of integrin and downregulation of cadherin), the initially circular region of cells (dotted gray contour) deforms and begins to spontaneously migrate as a cluster after ∼10 h (Movie S2). The black contour shows time progression of the mutated cells. (b and c) The cellular velocity field $\mathbf{v}$ within the entire tissue is depicted by the black arrows and the colormap shows the cell density, which varies from 0.95 (blue) to 1.05 (red) times the baseline density. To see this figure in color, go online.

We begin our analysis with a highly simplified model of a tumor. We consider a uniform population of cells located on a 400 × 400 μm periodic domain. We arbitrarily identify a 100 μm diameter circular region within this population of cells (Fig. 3 b, blue circular region). This circular region is the “tumor” that will be biophysically altered to determine whether these cells spontaneously migrate. We chose this simple picture because it is conceivable that in vitro experiments could be used to test the predictions from this scenario. The model is first simulated using uniform parameters (given in Table 1) within the entire domain. Over the course of the simulation, we track the location of the cells that started within the blue region. Forces within the epithelial layer produce velocities that cause the selected region of cells to deform some. However, over the course of a 50 h simulation, the center of mass of this region of cells does not migrate substantially away from where it started and always remains within the initial region (Fig. 3 b). Therefore, as expected, a cluster of nonmetastatic cells within a population of similar epithelial cells is predicted to remain fairly stationary.

Metastasis is often attributed to either EMT or MSG (14, 32); however, it may also involve amoeboid locomotion or cell blebbing (38, 39). A primary feature of EMT is upregulation of integrin (cell-ECM adhesion) and downregulation of cadherin (cell-cell adhesion), and this combination of upregulation of integrin and downregulation of cadherin has been identified in a number of cancer metastases (3). We, therefore, begin by exploring the effects of altering the cells in the circular region of our simulation by increasing cell-ECM adhesion (increasing the substrate drag coefficient ζ by a factor of 5) while decreasing cell-cell adhesion (reducing the cell-cell viscosity η by a factor of 5). We chose a factor of 5 because this is approximately the change in expression levels for N-cadherin that were measured in (31), and it is also the factor that we found to match changes in cell speed in the study on integrin-ligand binding (40). In striking contrast with the previous uniform simulation, we find that when cell-ECM adhesion is increased and cell-cell adhesion is decreased in a small region of cells, that this cluster of cells breaks free of its original location within ∼10 h and spontaneously migrates as a cluster of cells (Fig. 3 c). That is, our model predicts that upregulation of integrin along with downregulation of cadherin is sufficient to drive migration away from the initial tumor. In our simulations, this spontaneous migration of the cells is excited by the random initial condition that we choose for the polarization. Our previous work examined the linear stability of epithelial layers and found that there are parameter regimes for which the stationary epithelium is unstable (18). Therefore, if the biophysical parameters are in the correct regime, small random perturbations can lead to large-scale motions.

This result suggests that we can use our model to probe how the different biophysical parameters in our model independently affect evasion probability. We focus on the four parameters that are expected to be most relevant. As already mentioned, we expect cell-ECM and cell-cell adhesion to influence metastatic probability. In addition, Rho GTPases, which regulate cytoskeletal dynamics, are known to be involved in some cancers (15). For example, RhoC, which can activate formins and is upstream from myosin activation, has been identified as being involved in transitioning tumors to being malignant (15, 41, 42). Therefore, we also consider the effects of the biophysical parameters related to cytoskeletal force production, the propulsive force f_p and the dipole stress f_d. To analyze our results, we use the same 50 h simulations as previously described, with an initially circular domain of biophysically altered cells surrounded by a cell population defined by our baseline parameters (Table 1). We use random initial conditions for the cell polarizations and run 20 simulations for each parameter set. To use our results to make predictions about what is required for evasion, we compute the average velocity in the altered cell region and we also compute the evasion probability, which we define to be the percentage of simulations that produce a mass of cells that migrate outside the initial circular region.

Mutations that alter cell-ECM adhesion

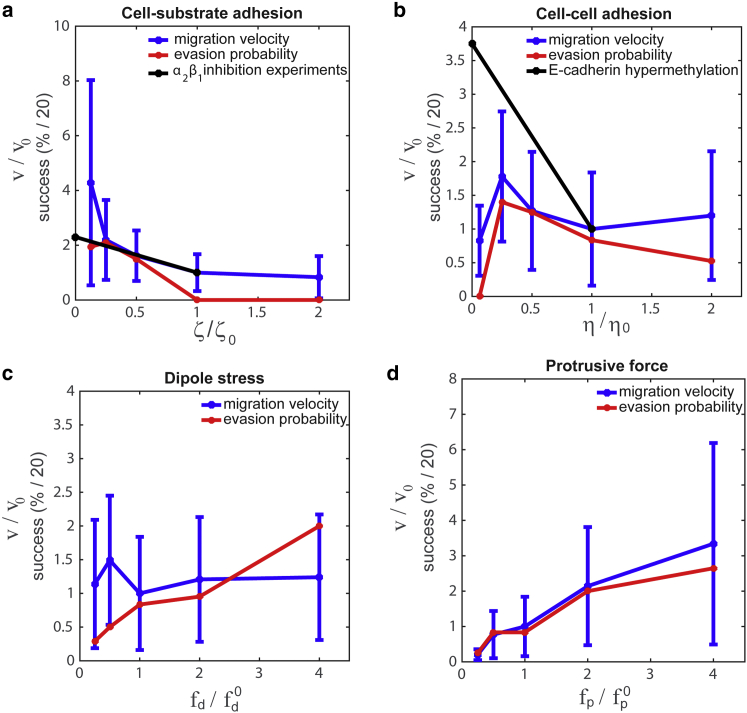
The integrins are the primary family of proteins that are used to adhere cells to the ECM, and alterations in the expression levels of integrins have been identified in numerous cancers (4). Some integrins, such as α₆β₄ and α_υβ₃, are increased during tumorogenesis; however, other integrins, such as α₅β₁, are lost in metastatic cells (4). The role of substrate adhesion on single-cell migration is bimodal: when adhesion is low, increases in the adhesion produce increases in cell speed, whereas at high adhesion, increasing the substrate adhesion slows cells down (40). This result suggests that propulsive force depends on substrate adhesion and therefore on integrin expression levels. Here we examine how substrate adhesion affects evasion at fixed propulsive force. We find that reducing substrate adhesion increases cell speed and evasion probability in our tumor simulations (Fig. 4 a), which is a consequence of the fact that reducing the substrate adhesion at fixed propulsive force is effectively like increasing the propulsive force and dipole stress at fixed adhesion. These results are consistent with the finding that some integrins, such as α₂β₁, can act as a metastasis suppressor in mouse models and human cancer. For example, it has been shown that loss of α₂β₁ leads to an increase in cell speed and an increase in metastases (Fig. 4 a) (43).

Figure 4.

How migration speed and evasion probability depend on cellular biophysics. (a) The migration velocity and evasion probability versus cell-ECM adhesion is shown. We find that decreasing the cell-ECM adhesion (ζ) leads to an increase in migration speed (blue line) and evasion probability (red line). This result agrees with findings that primary tumor cells lacking α₂β₁ integrin migrate at faster speeds than wild-type cells (black line is normalized data from (43)). The evasion probability is defined as the percent of simulations where the mutated cells escape the initial circular zone within 50 h. (b) Migration velocity (blue) and evasion probability (red) shows a maximum as a function of cell-cell adhesion strength η. The increase in migration speed as a function of adhesion at low values of η, is consistent with experiments using promotor methylation of E-cadherin (black line shows data from (47)). (c) The tumor model predicts that migration velocity (blue) is roughly independent of the dipole stress, but that increases in dipole stress increase the evasion probability (red). (d) Migration velocity (blue) and evasion probability increase with the protrusive force. To see this figure in color, go online.

The role of cell-cell adhesion in the transition to metastasis

As previously mentioned, a number of metastatic cancers, such as breast, prostate, and brain cancers, show a reduction in cadherin expression (44), which is presumed to cause a reduction in cell-cell adhesion. In breast cancer, downregulation of E-cadherin has been shown to be required for the initiation of metastatic outgrowth (45). In our model, cell-cell adhesion strength is dictated by the cell-cell viscosity η, which controls how easily cells can slide with respect to each other. We simulated our tumor model over a range from 1.25 to 20 dynes h/cm. We found that the migratory speed and evasion probability show bimodal behavior. For η < 2.5 dynes h/cm, increasing η leads to an increase in both speed and metastatic probability; however, above this value of η the speed and evasion probability decrease (Fig. 4 b). In vitro migration assays have shown that inactivation of E-cadherin via promotor methylation (which is the type of inactivation involved in EMT (46)) leads to an increase in collective migration speed (47), which is consistent with our model when η > 2.5 dynes h/cm (Fig. 4 b).

The role of active force production in the transition to metastasis

Many metastatic cancers show altered expression of Rho GTPases and other proteins that are involved in cytoskeletal dynamics. For example, ROCK plays an essential part in tumor cell invasion, possibly because of its activation of myosin (48, 49), the oncogene Ras downregulates Rac and leads to increased EMT activity (50), and, in connective tissue, tumor invasiveness is associated with increased contractile force generation (51). The actin cytoskeleton is the primary force-producing component that drives cell migration. In our model, the two parameters that control the active force production inside the cell are the contractile dipole stress f_d and the propulsive force f_p. Both of these parameters can be measured using single-cell assays. The dipole stress magnitude can be measured using traction-force microscopy (52), and the propulsive force is proportional to the average crawling speed. We examine the effect of each of these on migration speed and evasion probability in our tumor model. We find that although the dipole stress is not predicted to alter migration speed, that an increase in dipole stress by a factor of 10 increases the evasion probability from 5% to 40% (Fig. 4 c). On the other hand, increasing the propulsive force by a factor of 10 increase both migration speed and evasion probability by approximately the same factor (Fig. 4 d). It should be noted that the dipole stress also depends on cell shape. Therefore, changes in cell shape can alter the dipole-stress even if actomyosin contraction remains fairly constant.

Toward a more realistic tumor model

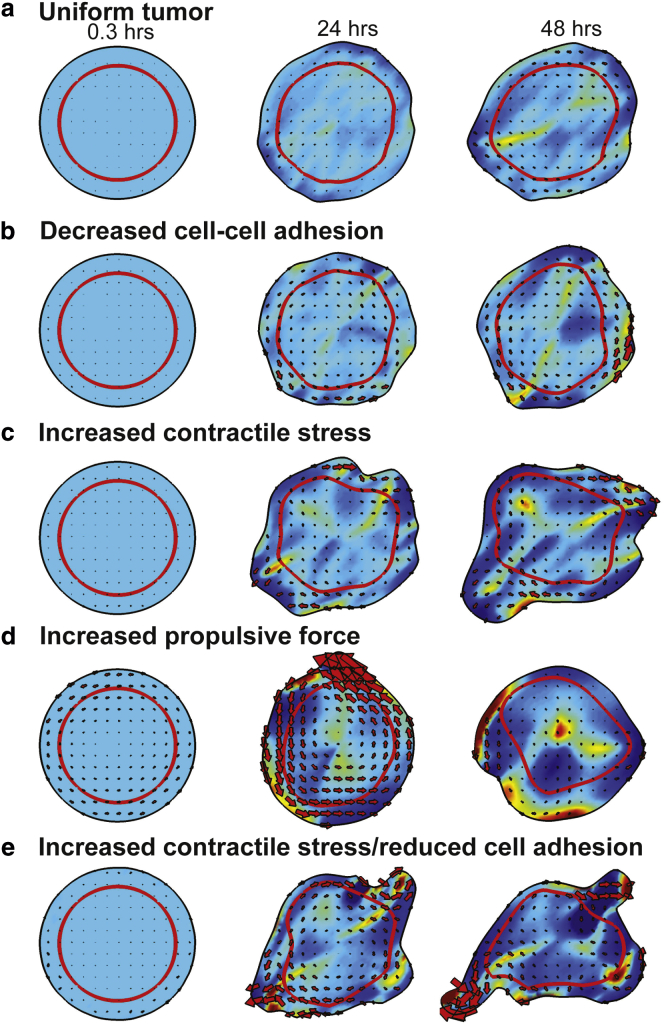
The preceding “tumor” model was highly simplified to define a system that could presumably be tested with in vitro experiments. To probe how our model handles a more realistic tumor, we consider a 2D solid tumor that is surrounded by ECM. Because the tumor mass is primarily cells, there is reduced ECM, and, therefore, the cell-ECM drag coefficient is low (ζ = 10⁴ dynes h/cm³). Because the tumor is surrounded by ECM, outside the initial tumor region, the cell-substrate adhesion is substantially higher (ζ = 10⁵ dynes h/cm³). We consider a tumor of 400 μm diameter and define a cortex region that is initially 50 μm in width (denoted by the red line in Fig. 5). If the cells in the cortex are identical to the cells in the core, then motion of the cells inside the tumor is slow and the tumor does not change much within a 48 h period (Fig. 5 a); however, we did notice a small rotation of the tumor with speeds near the periphery of 2–3 μm/h. We then investigated how altering the biophysics of the cells in the cortex affected the tumor dynamics. We began by decreasing the cell-cell adhesion to mimic downregulation of cadherin (Fig. 5 b). In these simulations, we saw increased rotation (with speeds of ∼10 μm/h) in the cortex and a roughening of the tumor boundary. However, over the 48 h simulation, the tumor shape did not change substantially. Increasing the contractile stress in the cortex produced qualitatively different behavior. For one, the tumor no longer showed uniform rotation. In addition, the tumor began to stretch and one region began to bud and pull away from the primary tumor (Fig. 5 c). We then examined how changing the propulsive force affected tumor dynamics. In these simulations, a large rotation of the tumor mass was seen during the first 24 h (Fig. 5 d). This rotation eventually died away, but we observed large deviations in cellular density throughout the tumor. Based on these findings, we hypothesized that increasing the contractile stress while lowering the cell-cell adhesion might produce more motile protrusions. Indeed, we found that increasing the contractile stress while decreasing the cell-cell adhesion lead to long finger-like projections that began to pinch off at around 48 h (Fig. 5 e).

Figure 5.

How biophysical alterations affect solid tumor dynamics. We simulated a 2D solid tumor model by considering an initially circular tumor surrounded by ECM. A region of cells near the periphery (red line) are biophysically altered. (a) When the cells at the periphery are unaltered, the tumor only deforms slightly within a 48 h period (Movie S3). (b) Lowering cell-cell adhesion (η = 2 dynes h/cm) to mimic a reduction in cadherin leads to larger flows in the cortical region. Although the tumor border roughens some, there are still no large-scale motions (Movie S4). (c) Increasing contractile stress (f_d = 2.5 dynes/cm) in the cortex leads to stretching of the cortex and a budding region that pulls away from the primary tumor (Movie S5). (d) Increasing the propulsive force (f_p = 1000 dynes/cm²) in the cortex produced an initially large-scale rotation of the tumor that died down over time. In addition, much larger variations were observed in cell density (colormap) when larger propulsive forces were in the cortex (Movie S6). The red arrows show the local velocities within the tumor. (e) Increasing the contractile stress (f_d = 2.5 dynes/cm) while simultaneously decreasing cell-cell adhesion (η = 2 dynes h/cm) in the cortex produces thin protrusions off the tumor that begin to pinch off at around 48 h (Movie S7). The red arrows show the local velocities within the tumor. Except where otherwise noted, the parameters that are used are η = 10 dynes h/cm, f_d = 0.5 dynes/cm, f_p = 100 dynes/cm², ζ = 10⁴ dynes h/cm³ (inside the initial tumor region), 10⁵ dynes h/cm³ (outside the initial tumor region), and σ₀ = 10⁻⁸ dynes/cm, c₀ = 1. To see this figure in color, go online.

Discussion

The large heterogeneity in metastatic cancer cells at the genomic and proteomic levels suggests that the metastatic potential of a cell is dictated by a large number of functionally redundant mechanisms. What criteria then determine whether a cell or group of cells are malignant? Because metastasis involves cellular migration, we propose that there are a countable number of biophysical parameters that regulate metastatic potential. To test this hypothesis, we began by validating an existing biophysical model for collective migration in epithelial tissues (17, 18). We showed that this model can accurately reproduce migration rates in wound healing assays where cancer-relevant cell lines were perturbed to alter cell-cell adhesion or actomyosin contraction.

We then used this model to study a simplified picture of the transition of a tumor from benign to metastatic by treating the main mass of a primary tumor as being comprised of a biophysically uniform population of cells. We showed that subregions of this uniform population remain fairly stationary. However, when a small region within the population is “mutated” by altering the biophysical parameters, it is possible to get spontaneous migration of the mutated population of cells, which therefore predicts changes that may be involved in the early stages of metastasis. One such alteration was the simultaneous increase of cell-ECM adhesion concomitant with decrease of cell-cell viscosity, which mimics the upregulation of integrin along with downregulation of cadherin that is observed in a number of metastases (3). In addition, we showed the effects that alterations to cell-substrate adhesion, cell-cell adhesion, contractile forces, and propulsive forces have on the cell speed and the evasion probability for tumor cells. Specifically, we showed that cell migration speed was roughly proportional to propulsive force, inversely proportional to cell-ECM adhesion, and not strongly dependent on dipole stress or cell-cell adhesion, whereas the evasion probability (the likelihood that a region of mutated cells will migrate a substantial distance (∼100 μm) in a short amount of time (∼50 h)) increased with dipole stress and propulsive force, decreased with cell-ECM adhesion, and depended in a biphasic manner with cell-cell adhesion.

To investigate a more realistic tumor model, we then considered a solid tumor where cells in a cortical region are biophysically altered. In many cases, we found that there is a tendency for the tumor to rotate. Only when we altered the contractile stress did we disrupt net rotation and also got a region of the cortex to bud off from the primary tumor mass (Fig. 5 c). Experiments looking at epithelial acini, which are a spherical arrangement of cells that are considered to be precursors to duct formation, observe rotation of the acinar structure; however, cancer cells under similar conditions do not rotate (53, 54). Our results seem to suggest that our model may be capturing aspects of this behavior, but a more detailed analysis will need to be done to fully examine this question.

Whereas much of the work in the transition to metastasis has focused on the genetic mutations and altered expression that occurs during this process, we propose a complementary approach to investigate the biophysical alterations that produce metastasis. We use a simplified model that considers the tumor to be a 2D epithelial tissue where the ECM and cells are treated as uniform continua. Although actual tumors are more complicated three-dimensional objects with discrete cells and an ECM that is actively remodeled during the progression of cancer, the setup of our model is tractable for experimental testing. For example, the predictions of this model could be tested using single-cell measurements to probe the biophysical parameters of single cell, such as crawling speed and traction force. If two populations of biophysically different cell types are co-cultured in a 2D confluent monolayer, it would allow for the measurement of the migration of subpopulations of cells that could be compared with our predictions.

Author Contributions

C.W.W. and P.L. designed and performed the research, analyzed the data, and wrote the article.

Editor: Fazoil Ataullakhanov

Supporting Material

Movie S1. Our Model

In the absence of mutation, our model predicts that subregions of an epithelial tissue are relatively immobile. We consider an initially circular subregion of cells with a 100 μm diameter (denoted by the blue contour). These cells have the same biophysical parameters as the exterior region. We simulate the model for a total time of 50 h and track the movement of the subregion of cells. This initially circular region deforms some over the course of the simulation, as shown by the red contour, but the center of mass remains within the initial circular region. The cellular velocity field v within the entire tissue is depicted by the black arrows and the colormap shows the cell density, which varies by less than 5%. The colormap shows the density from 0.95 (blue) to 1.05 (red) times the baseline density.

Movie S2. Specific Biophysical Alterations to the Subregion Can Lead to Metastasis

Using the same procedure as described in Movie S1, we examine how increasing the cell-ECM and decreasing the cell-cell adhesion by a factor of 5 (which represents upregulation of integrin and downregulation of cadherin) affects the movement of the subregion. For this case, the initially circular region of cells (blue contour) deforms and begins to spontaneously migrate as a cluster after approximately 10 h.

Movie S3. Simulation of a Solid Tumor Where an Initially Circular Cell-Filled Region Is Surrounded by ECM

In the cell-filled region, the cell-substrate drag is low (ζ = 10⁴ dynes h/cm³), whereas outside this region, the cell-substrate drag coefficient is higher (ζ = 10⁵ dynes h/cm³). The red line denotes the boundary between the core and cortex of the tumor. In this simulation, the cells in the core are identical to the cells in the cortex. The parameters that are used are η = 10 dynes h/cm, f_d = 0.5 dynes/cm, f_p = 100 dynes/cm², σ₀ = 10^-8 dynes/cm, and c₀ = 1. The colormap shows the density and the arrows the local velocity.

Movie S4. Simulation of a Solid Tumor as in Movie S3

All the parameters are the same except that the cell-cell viscosity is decreased to η = 2 dynes h/cm to mimic down-regulation of cadherin.

Movie S5. Simulation of a Solid Tumor as in Movie S3

All the parameters are the same except that the intracellular contractile stress is increased to f_d = 2.5 dynes/cm.

Movie S6. Simulation of a Solid Tumor as in Movie S3

All the parameters are the same except that the propulsive force is increased to f_p = 1000 dynes/cm².

Movie S7. Simulation of a Solid Tumor as in Movie S3

All the parameters are the same except that the contractile stress is increased to f_p = 1000 dynes/cm² and the cell-cell viscosity is decreased to η = 2 dynes h/cm.