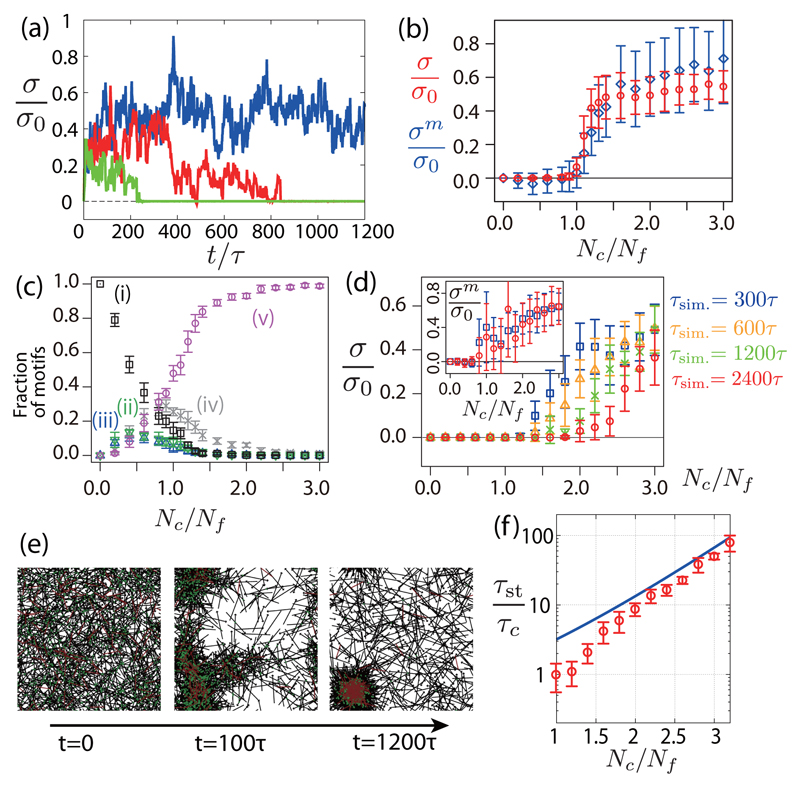
Fig. 3.

Stress in a network of motors and filaments, with and without cross-linker turnover. (a) Time evolution of the normalized stress σ/σ₀ for τ_c⁻¹ = 0, N_c = 1.2N_f (blue), τ_c = 100τ, N_c = 1.6 N_f (red) and τ_c = 100τ, N_c = 1.2N_f (green) (σ₀ = f₀l_mN_m/W²). (b) Steady-state isotropic stress σ (circles) and motor stress σ^m (diamonds) as a function of the cross-linkers number N_c for τ_c⁻¹ = 0. (c) Fraction of different configurations in Figs. 2(i)-2(v) at steady state as a function of the cross-linker number N_c for τ_c⁻¹ = 0. (d) Isotropic stress σ as a function of the cross-linker number N_c, for a finite cross-linker lifetime τ_c = 100τ, and for several simulation times (τ_sim. = 300, 600, 1200 and 2400τ). Stress within the motors σ^m is shown in the inset for τ_sim. = 300 and 2400τ. (e) Snapshots of a simulated network with cross-linker turnover (N_c = 1.2N_f, τ_c = 100τ). (f) Stress decay time τ_st as a function of the cross-linker number N_c with cross-linker turnover (τ_c = 100τ). Solid line, theoretical prediction (see the main text). Other parameters are N_f = 1000, N_m = 100, τ_f⁻¹ = 0, $k_{on}^c{\tau }_c=20$, l_f = 2l_m, W = 10l_m,τ_m = 100τ, and $k_{on}^m\tau =20$.