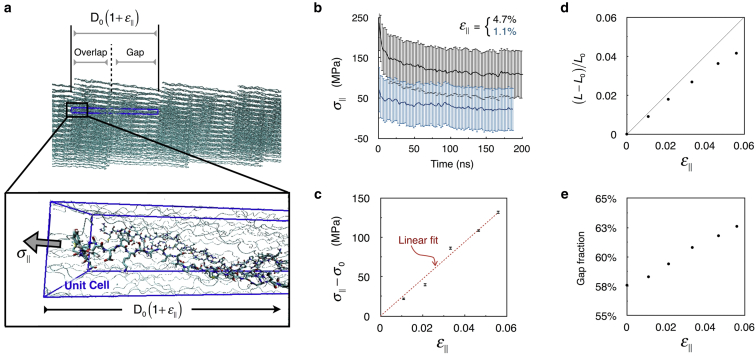
Figure 3.

Constant-strain MD simulations of the crystallographic unit cell under periodic boundary conditions. (a) Snapshot of the MD simulation illustrating the unit cell (blue box), the strained lattice constant $\left|\mathbf{a}\right|=D_0\left(1+{ϵ}_{\parallel }\right)$, and the component of the virial stress tensor parallel to the fibril axis, ${\sigma }_{\parallel }$. (b) Time evolution of the ${\sigma }_{\parallel }$ in two different constant-strain simulations, one in which ${ϵ}_{\parallel }=0.011$, and the other in which ${ϵ}_{\parallel }=0.047$. The vertical lines represent fluctuations in ${\sigma }_{\parallel }$ observed over 2 ns time intervals. (c) Stress-strain relationship estimated for five different strain values. $\langle {\sigma }_{\parallel }\rangle$ values are averages over the final 20 ns of the constant-strain simulations, and the standard errors are obtained via block averaging. (d) Relationship between the fractional change in the length of the triple-helix (L), and the applied strain, estimated from the final 20 ns of constant-strain simulations. $L_0$ is the length of the triple helix in the zero-strain simulation. (e) Relationship between the gap fraction and the applied strain, estimated from the final 20 ns of constant-strain simulations. To see this figure in color, go online.