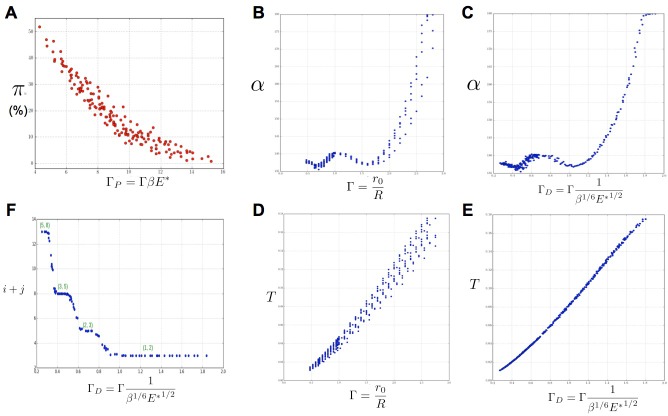
Figure 6. Key parameters controlling phyllotaxis phenotypes in the stochastic model.

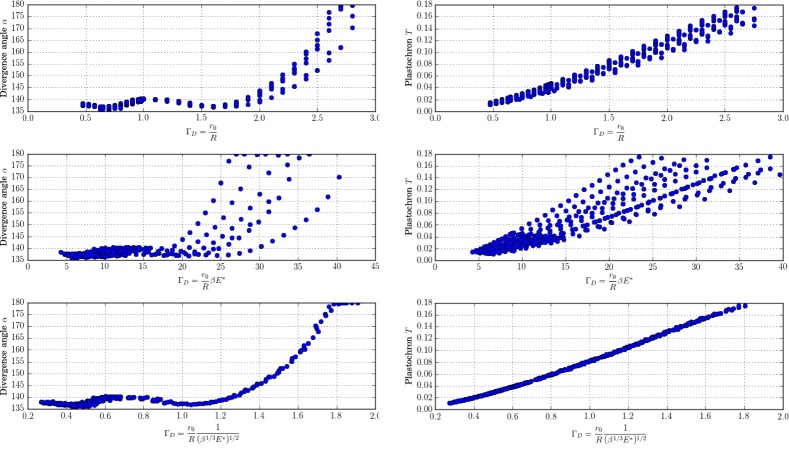
Phyllotaxis sequences were simulated for a range of values of each parameter ${\displaystyle \beta }$, ${\displaystyle E^{\ast }}$, ${\displaystyle \mathrm{\Gamma }}$. Each point in the graph corresponds to a particular triplet of parameter values and represents the average value over 60 simulated sequences for this triplet. (A) Global amount of perturbation ${\displaystyle \pi }$ as a function of the new control parameter ${\displaystyle {\mathrm{\Gamma }}_P=\mathrm{\Gamma }\beta E^{\ast }}$. (B) Divergence angle ${\displaystyle \alpha }$ as a function of the control parameter ${\displaystyle \mathrm{\Gamma }}$ of the classical model on the Fibonacci branch. (C) Divergence angle ${\displaystyle \alpha }$ as a function of the new control parameter ${\displaystyle {\mathrm{\Gamma }}_D=\mathrm{\Gamma }\frac{1}{{\beta }^{1/6}{E}^{\ast 1/2}}}$ on the Fibonacci branch (here, we assume s = 3, see Appendix 1—figure 6 for more details). (D) Plastochron ${\displaystyle T}$ as a function of control parameter of the classical model ${\displaystyle \mathrm{\Gamma }}$. (E) Plastochron ${\displaystyle T}$ as a function of the new control parameter ${\displaystyle {\mathrm{\Gamma }}_D}$. (F) Parastichy modes ${\displaystyle (i,j)}$ identified in simulated sequences as a function of ${\displaystyle {\mathrm{\Gamma }}_D}$. Modes ${\displaystyle (i,j)}$ are represented by a point ${\displaystyle i+j}$. The main modes (1,2), (2,3) … correspond to well marked steps. (Figure 5—source data 1)

DOI: http://dx.doi.org/10.7554/eLife.14093.013

Figure 6—figure supplement 1. New control parameter ${\displaystyle {\mathrm{\Gamma }}_D}$ for divergence angle and plastochrons.

Each graph is made up of points that correspond to different values of the parameters ${\displaystyle \mathrm{\Gamma },\beta ,E^{\ast }}$ of the stochastic model. Left column: different trials to define a control parameter for divergence angles ${\displaystyle \alpha }$. Right column: different tries to define a control parameter for the plastochrons. For the parameter ${\displaystyle {\mathrm{\Gamma }}_D=\mathrm{\Gamma }\frac{1}{({\beta }^{1/3}{E}^{\ast }{)}^{1/2}}}$, both clouds of points collapse on a single curve (we assume here that s = 3, see Appendix 1—figure 6 for more details).

DOI: http://dx.doi.org/10.7554/eLife.14093.014