Skip to main content
PMC home page
British Journal of Cancer logoLink to British Journal of Cancer
. 2016 Jul 12;115(2):195–202. doi: 10.1038/bjc.2016.171

Tumour and immune cell dynamics explain the PSA bounce after prostate cancer brachytherapy

Yoichiro Yamamoto 1,2,*, Chetan P Offord 3,✠, Go Kimura 4, Shigehiko Kuribayashi 5, Hayato Takeda 4, Shinichi Tsuchiya 2,6, Hisashi Shimojo 1, Hiroyuki Kanno 1, Ivana Bozic 7, Martin A Nowak 7, Željko Bajzer 8, David Dingli 3,9
PMCID: PMC4947697  PMID: 27404586

Abstract

Background:

Interstitial brachytherapy for localised prostate cancer may be followed by transient increases in prostate-specific antigen (PSA) that resolve without therapy. Such PSA bounces may be associated with an improved outcome but often cause alarm in the patient and physician, and have defied explanation.

Methods:

We developed a mathematical model to capture the interactions between the tumour, radiation and anti-tumour immune response. The model was fitted to data from a large cohort of patients treated exclusively with interstitial brachytherapy. Immunohistological analysis for T-cell infiltration within the same tumours was also performed.

Results:

Our minimal model captures well the dynamics of the tumour after therapy, and suggests that a strong anti-tumour immune response coupled with the therapeutic effect of radiation on the tumour is responsible for the PSA bounce. Patients who experience a PSA bounce had a higher density of CD3 and CD8 cells within the tumour that likely contribute to the PSA bounce and the overall better outcomes observed.

Conclusions:

Our observations provide a novel and unifying explanation for the PSA bounce in patients with early prostate cancer and also have implications for the use of immune-based therapies in such patients to improve outcomes.

Keywords: prostate cancer, PSA bounce, immune response, dynamics, brachytherapy

Cancers are complex diseases often causing unexpected phenomena. Prostate cancer is one of the most common types of male cancer. Interstitial brachytherapy with the implantation of radioactive iodine-125 (125I) seeds in the prostate is one of the standard treatments for localised and low-grade prostate cancer (Ash et al, 2000). Prostate-specific antigen (PSA) is a sensitive marker of tumour burden before and after prostate cancer therapy (Stamey et al, 1987). After prostate brachytherapy, some patients will experience an asymptomatic and temporary PSA increase followed by spontaneous reduction to the nadir (Patel et al, 2004) that may mimic cancer relapse with the exception that the PSA will fall without therapy. This phenomenon is called a PSA bounce. Although PSA bounce can be of concern for both the patient and physician, paradoxically, it is often associated with an improved prognosis (Patel et al, 2004; Ciezki et al, 2006; Mitchell et al, 2008; Bernstein et al, 2013). To date, no satisfactory explanation for this phenomenon has been forthcoming (Chira et al, 2013).

Wallner et al first described the PSA bounce after prostate brachytherapy in 1997 (Wallner and Dattoli, 1997). Typically, a PSA bounce occurs 1–2 years after implantation of radioactive seeds (Caloglu and Ciezki, 2009). However, in that time interval, the 125I implanted would have lost ∼98% of the activity, given the 59.4 day half-life of the isotope (Critz et al, 2000). Several hypotheses have been proposed as a cause of the PSA bounce: bacterial and radiation prostatitis (Critz et al, 2000), a late radiation effect (Mitchell et al, 2008) and the inter-assay noise intrinsic to PSA measurements. However, each hypothesis cannot provide sufficient explanation for the delayed occurrence and the long duration of such a PSA bounce, that can last for more than 8 months (Critz et al, 2003; Bostancic et al, 2007). In addition, the PSA bounce is not unique to brachytherapy and sometimes occurs in patients treated with external beam radiotherapy alone (Horwitz et al, 2006).

Recently, Kirilova et al (2011) reported 3D MR spectroscopic assessments of the prostate during PSA bounce after brachytherapy. They analysed the metabolic activity during the bounce and suggested that the bounce could be related to unexplained inflammation. In the nineteenth century, Rudolf Virchow observed the presence of leucocytes within tumours, and provided the first suggestion of a link between cancer and inflammation (Grivennikov et al, 2010). More recently, several studies reported that infiltration of T cells in solid tumours was a positive prognostic factor (Clark, 1991; Nakano et al, 2001; Sharma et al, 2007), and the impact of CD8+ lymphocytes on prognosis is widely accepted. Cytotoxic CD8+ T cells can directly attack target tumour cells, binding and releasing cytotoxic perforin and granzymes (Chavez-Galan et al, 2009). Therefore, the anti-tumour immune response to solid cancer is increasingly attracting attention.

The dynamics of PSA level after brachytherapy are suitable for mathematical analysis because the PSA levels of all patients are measured periodically as part of routine medical care. Imperfect as the PSA may be due to disease heterogeneity, and the possibility that PSA production decreases as the tumour becomes more advanced, decisions on disease status (continued response or progression) and the need for additional therapy are partly based on this result. We can take radioactive isotope decay and the biological half-life of PSA in the blood into account mathematically. In this study, we utilise a mathematical model to understand the mechanisms behind the PSA bounce, propose a hypothesis to explain it and provide experimental proof in support of this proposal.

Materials and methods

Subjects

Patients with T1-T2N0M0 prostate cancer treated with 125I prostate brachytherapy between 2006 and 2010 at Nippon Medical School Hospital were reviewed. Patients who received hormonal therapy before and/or after brachytherapy were excluded. This study was limited to patients with a minimum of 2 years of follow-up and with low or intermediate risk disease according to the D'Amico classification (D'Amico et al, 1998). Prostate-specific antigen levels were generally checked every 3 months, but the interval between PSA determinations varied depending on symptoms and PSA level. All patients were treated using the interactive plan technique (Stock et al, 1995). The prescribed dose to the prostate was set at 160 Gy. A total of 63 patients, aged 48–81 years (66.3±7.0 years) (mean±s.d.), were included in this study. This study was performed according to the Declaration of Helsinki and was approved by the ethical committee, Nippon Medical School Hospital, Japan.

Definitions of PSA bounce

The definition of PSA bounce varies widely in published reports. In this analysis, a PSA bounce was defined as an increase in PSA of 0.2 ng ml−1 (Critz et al, 2000) or a greater than 15% relative increase in PSA from a prior value, as long as it was an increase of at least 0.1 ng ml−1 (known laboratory variability) (Prestigiacomo and Stamey, 1996) over the nadir level and followed by a return to the nadir levels or lower without additional treatment. The duration of the bounce was defined as the time from the pre-bounce nadir to the first PSA level below this nadir. The time to onset was the first date when the PSA increased to a level that defined the presence of a PSA bounce.

Histological classification of tumours

We histologically classified tumours based on the World Health Organization (WHO) classification criteria. At least three pathologists diagnosed and scored all the cases independently and reached collective consensus if the initial independent diagnosis was different.

Immunohistochemical staining and immune cell counting

Immunohistochemical analyses of CD3 and CD8 were performed on biopsies of the prostate obtained between 2 and 4 weeks before brachytherapy. All biopsies were reviewed to confirm the diagnosis and those biopsies that contained sufficient area (>0.2 mm2) of cancer tissue to evaluate the density of CD3+ and CD8+ cells were analysed further. As a consequence, 35 cases were analysed: 21 cases with PSA bounce aged 48–79 years (63.6±7.8 years) and 14 with no-bounce aged 61–81 years (71.1±6.3 years). All samples were fixed in 10% formalin and embedded in paraffin. The tumour samples were sectioned at a thickness of 3 μm. Immunohistochemical staining was performed by using indirect immunoperoxidase techniques. The primary antibodies for staining CD3 and CD8 were rabbit polyclonal CD3 antibody (ABGENT, San Diego, CA, USA) and rabbit polyclonal CD8 antibody (ABGENT), respectively, both at a dilution of 1 : 50. All sections were counterstained with haematoxylin. All glass slides were captured using Hamamatsu NanoZoomer 2.0-HT Slide Scanner (Hamamatsu Photonics, Hamamatsu City, Japan), and virtual slides were made. Cancer areas that the pathologist detected on the slide were digitally measured and the number of CD3+ and CD8+ cells in this cancer area was counted manually. The density of cells per mm2 was calculated from these data.

Mathematical modelling

In order to understand the dynamics of PSA and the tumour after interstitial brachytherapy, we developed a mathematical model that captures the dynamic interactions between PSA concentration (z), the tumour cell (x) population and immune response to the tumour (y). Note that only the PSA concentration was measured serially in time. Our model is defined by the following set of differential equations:

graphic file with name bjc2016171e1.jpg
graphic file with name bjc2016171e2.jpg

and

graphic file with name bjc2016171e3.jpg

The term (p1−s1e−λt)x represents the effective growth of tumour cells as the difference between exponential growth and destruction of cells by radiation. As the half-life of 125I is known (59.4 days), the value of λ is fixed. Given that the isotope is injected in sealed containers (‘seeds'), there is no loss of isotope from the tumour site and it will ultimately decay within the confines of the tumour cell population. The second term in Equation (1a) is the effective killing of tumour cells by the immune system that occurs with rate constant δ. The function takes into account the potential inhibitory effect of the tumour on an effective immune response when the tumour (x) is large (Schietinger et al, 2012; Schietinger and Greenberg, 2014). In such a case, the denominator would be large. The exponent q can be chosen or determined by fitting. Our model has 12 parameters, however, we have fixed q=5 and u=30, and as a result, the model has 10 free parameters.

The term 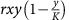Inline graphic in Equation (2a) for immune cell dynamics represents the increase in immunologically active cells as a result of a response to the tumour. We assume that K=1000C, where C refers to the average immune cell density found within the tumour biopsy specimens and can only enlarge 1000-fold compared with baseline. Thus, we assume that the immune response has an internal control. The second term in Equation (2a) represents the reduction of the immune cells in the vicinity of the tumour as a result of radiation and by standard degradation (v). We assume that immune cells are more sensitive to radiation than tumour cells and therefore, f>1.

The first term (p+se−λt)x in Equation (3) represents the effective increase in PSA as the tumour grows where px reflects the PSA produced because of tumour cell growth and se−λtx is the increase in PSA due to destruction of tumour cells by radiation. Prostate-specific antigen is cleared from the circulation with rate constant u.

We normalised the variables of Equations (1, 2, 3) so that 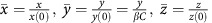Inline graphic, so that the initial conditions become 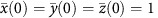Inline graphic, and the equations are accordingly transformed (see Supplementary Material). Here, parameter β is introduced to enable estimation of the initial value of the immune response.

A number of constraints were imposed on the model:

  1. The half-life of PSA is estimated to be between 2 and 3 days (Stamey et al, 1987).

  2. In the absence of radiation, (s 1=s=0), the parameters must be constrained such that all equations have a positive initial velocity.

The model was fitted to individual patient data sets comprising the PSA and the respective time, it was sampled before and after definitive therapy with interstitial brachytherapy. Fitting was performed by weighted least squares methodology using the Simplex Induction Hybrid optimisation described previously (Offord and Bajzer, 2006) and the goodness of fit determined by the Chi square test.

Given the complexity of the immune response, and the increasing relevance of a cytotoxic immune response to the tumour with the development of immune checkpoint targeted therapy, we elected to model only a T-cell response to the tumour. Various models have been published in this regard and therefore, we have compared the fits based on our model to fits based on three other models that describe the immune response to tumour growth (Stepanova, 1980; Kuznetsov et al, 1994; Forys et al, 2006). Within the context of our model for PSA dynamics after brachytherapy, these models correspond to the following equations:

graphic file with name bjc2016171e7.jpg
graphic file with name bjc2016171e8.jpg

where φ(x)=x in our model and the models of Forys et al and Stepanova, while 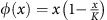Inline graphic corresponds to the model of Kuznetsov et al. The rate term 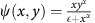Inline graphic corresponds to the model of Forys et al and when α=1, this corresponds with the model of Kuznetsov et al. Finally, 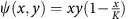Inline graphic reflects the model by Stepanova, and in the latter case, ω=0. The equation for PSA concentration is the same for all models.

Model fitting and parameter estimation

The fits for all considered models were compared with the modified Akaike Information Criterion (AIC) (Hurvich and Tsai, 1989; Fang, 2011), which takes into account the number of free parameters and indicates which model is preferable. We fitted two models to the individual patient data: in one model, only Equations (1a) and (3) were included (the immune system excluded), while in the second approach, the full model (Equations (1, 2, 3)) was fitted to the data. We used the modified AIC to determine which model provided the preferred fit for the data (Hurvich and Tsai, 1989; Fang, 2011). In addition, we performed an extensive analysis to determine the impact of each parameter individually on the ability of the model to capture the PSA bounce. Thus, for each patient, we varied one parameter at a time across the range of parameter values obtained by the original global fitting (as reported in Table 1), and while keeping the other parameters constant, we fitted to model to the data and determined the goodness of fit using the Chi square statistic. Our analysis showed that the parameter s had the least impact on the goodness of fits. Given that our model had 10 free parameters, we restricted our analysis to patients for whom a minimum of 12 data points were available.

Table 1. Parameter estimates based on model fitting.

Parametera P1 s1 P s β δ a r f v
Bounce 1.06 3.27 41.80 15.27 2.90 21.30 0.38 7.42 2.36 0.85
Range 0.1–3.73 1.00–6.46 30.01–60.0 1.07–101.37 0.22–4.88 0.02–50.00 0.08–1.94 1.78–195.47 1.25–11.02 0.01–14.06
No Bounce 1.03 3.95 43.17 15.46 1.75 21.01 0.33 10.95 3.20 0.60
Range 0.11–6.36 1.00–6.84 30.02–59.99 1.05–60.54 0.01–4.88 0.03–50.00 0.08–0.58 1.28–65.08 1.25–17.38 0.01–4.90
P value 0.92 0.18 0.68 0.98 0.01 0.95 0.50 0.50 0.33 0.59
Open in a new tab
a

The time unit for all parameters, except β and f which are non-dimensional, are 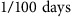Inline graphic.

Statistical analysis

Logistic regression was used to determine statistical significance for correlation between patient characteristics and whether or not they experienced a bounce. Fischer's exact test was used for categorical data and Student's t-test for continuous data. Reported values are number of patients with percentage for categorical data or averages or medians with minimum and maximum values for continuous data. Tests were all two-tailed, and required P<0.05 for statistical significance. The statistical significance of correlations between the parameters were determined using Spearman's rho using a one-sided test.

Results

Clinical characteristics

The clinical characteristics of our patient cohort are reported in Table 2. A total of 63 patients were included. On the basis of the established definitions of a PSA bounce, 40 (63%) of our patients experienced such a transient increase in PSA after therapy, while 23 (37%) did not have a bounce. As reported by others (Toledano et al, 2006; Caloglu and Ciezki, 2009), the patients with a bounce tended to be younger (median age of 65 years vs 69, P=0.01). There was no difference in the Gleason score, tumour stage or prostate volume between the two groups at the time of initiation of radiation therapy. The dose of radiation given did not differ between the two cohorts. Patients who subsequently developed a bounce in their PSA often had a slower reduction in PSA (determined from the value of the slope of the decay of PSA) after brachytherapy and almost half (13/27) had a transient increase in PSA at the first follow-up visit after brachytherapy compared with only 2 of 23 patients who did not develop a bounce (P=0.04). The PSA bounce was observed at a median of 12 months after the initiation of therapy while the median duration of a PSA bounce was 9 months. These observations are similar to what has been reported by others (Caloglu and Ciezki, 2009; Bernstein et al, 2013; Chira et al, 2013).

Table 2. Clinical characteristics of patient cohort.

Characteristic PSA bounce No bounce P value
Patients (n) 40 23  
Age (years) 65 (48–79) 69 (58–81) 0.01
Follow-up (days) 1432 (825–2579) 1273 (962–2428) 0.06
Gleason score      
 <7 30 12 0.1
 =7 10 11  
Tumour stage      
 ⩽1c 14 5 0.39
 ⩾2a 26 18  
Radiation dose (P-D90) 189 (152–260) 190 (140–233) 0.37
Prostate volume (cm3) 24.3 (14.4–35.1) 25.0 (17.4–35.3) 0.64
Rad dose/prostate volume 7.58 (5.29–13.75) 7.52 (4.85–9.84) 0.23
Pre-therapy PSA (ng ml−1) 7.58 (2.3–10.9) 5.23 (2.6–21.0) 0.2
Decrease in PSA at first follow-up 0.24 (−2.11–0.81) 0.48 (−0.96–0.76) 0.04
Open in a new tab

Abbreviation: PSA=prostate-specific antigen. The bold is used to highlight statistically significant differences in parameters between groups.

Model fitting and parameter comparisons

We fitted our mathematical model (Equations (1a, 2a and 3)) to each individual patient data set as reported in the Materials and Methods. We had a median of 17 independent data points for PSA for each patient (range: 12–35). Two fitting procedures were performed: (i) one approach utilised Equations (1a) and (3) only with the second right hand term in Equation (1a) excluded to eliminate the immune response. (ii) We also fitted the 3-equation model to the data (Equations (1a, 2a and 3)). It should be noted that it is mathematically impossible for a model with only Equation (1a) (with the second right hand term excluded to eliminate the immune response) and (Equation (3)) to capture the PSA dynamics that include the bounce. We fitted the two models to the patient data and determined the AIC for each model. In the vast majority of cases, the AIC preferred the 3-equation model as the better fit even in the absence of a PSA bounce. This suggests that even in patients without a PSA bounce, the system of equations that includes the immune response is superior to understand PSA dynamics.

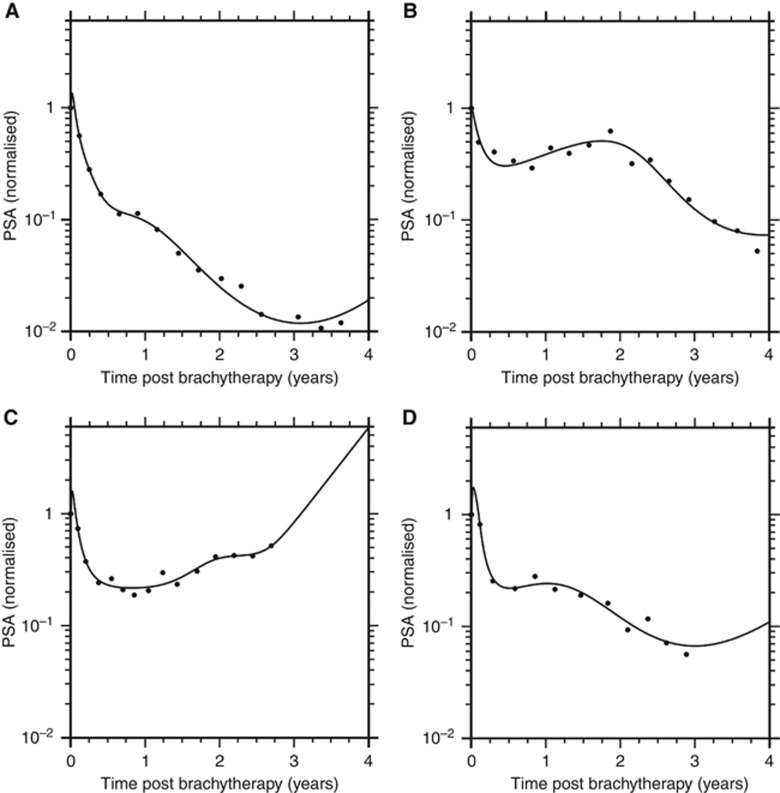
We performed fitting procedures using the model with Equations (1a, 2a and 3) to determine the optimal value of q and found that q=5 was an appropriate exponent. The parameter estimates for the model are reported in Table 1. As can be seen from Figure 1, the model fit well a variety of scenarios including (i) monotonic decline in PSA, (ii) patients with a bounce in PSA, (iii) relapse of the disease and (iv) initial increase in PSA followed by significant reduction in tumour burden.

Figure 1.

Figure 1

Open in a new tab

Prostate-specific antigen dynamics and model fitting. Serial PSA values for each individual patient were fitted to the model (solid line). The model provides excellent fits for patients demonstrating (A) successful therapy, (B) PSA bounce, large in magnitude and long duration, (C) tumour relapse and (D) PSA bounce that is both small in magnitude and short in duration, with a small increase in PSA immediately following first follow-up from brachytherapy.

Given that other models of tumour–immune system interactions have been published, we also fitted three other models (see Equations (1b and 2b) in ‘Mathematical Model') to the individual patient data, and with the AIC determined that our model was the preferred option for fitting. A simpler model limited to Equations (1a and 3) or uncoupling the immune response from the model by imposing δ=0 cannot fit the PSA data whenever there is a bounce. Therefore, the model as presented is an adequate and minimal model that can fit the clinical data in the presence/absence of a bounce.

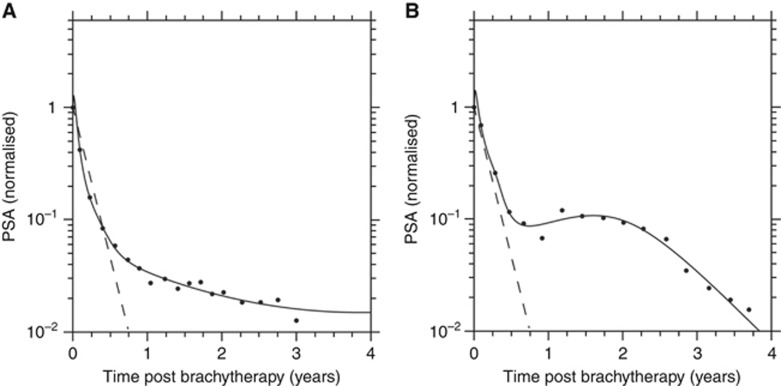
The isotope decays monotonically without any escape from the tumour. A comparison of PSA reduction with the concomitant intra-tumoural isotope decay shows that these two processes occur essentially in parallel (Figure 2) and the bounce invariably occurs after the isotope has decayed. Therefore, the PSA bounce cannot be explained by the effect of radiation, and as a consequence, we hypothesised that the PSA bounce was due to the differential immune response to the tumour and constructed the model to take this into account (see Materials and Methods).

Figure 2.

Figure 2

Open in a new tab

Prostate-specific antigen values and isotope levels. Individual patient PSA values and model fits (solid line) plotted against normalised 125I levels (dotted line). Isotope levels in both patients without PSA bounce (A) and with bounce (B) show PSA reduction corresponding with the presence of 125I in the first 6 months. However, PSA dynamics during the time of bounce in (B) cannot be due to continued isotope because the PSA bounce occurs after the isotope has effectively decayed.

Parameter comparisons

We wanted to determine whether any of the parameters of the model were significantly different in patients with and without a PSA bounce after interstitial brachytherapy. The only parameter that was statistically significantly different between the patients with and without a bounce was β: for patients with a PSA bounce β=2.90 compared with patients without a PSA bounce (β=1.75). The difference in β was statistically significant (P=0.01). In our model, β reflects the strength of the anti-tumour immune response at the start of therapy. Our results suggest that patients who experienced a PSA bounce have a stronger anti-tumour immune response compared with patients without the bounce.

Given the observation that the PSA bounce tends to occur in younger patients (Toledano et al, 2006; Caloglu and Ciezki, 2009), we performed a correlation analysis between patient age and the model estimate of β for each patient. We found a statistically significant negative correlation between the two parameters: ρ=−0.221, P=0.041, suggesting that the strength of the immune response decreases with age. Note that patient age was not directly included in the model and the result of this correlation provides further support for our model.

Immunohistochemistry

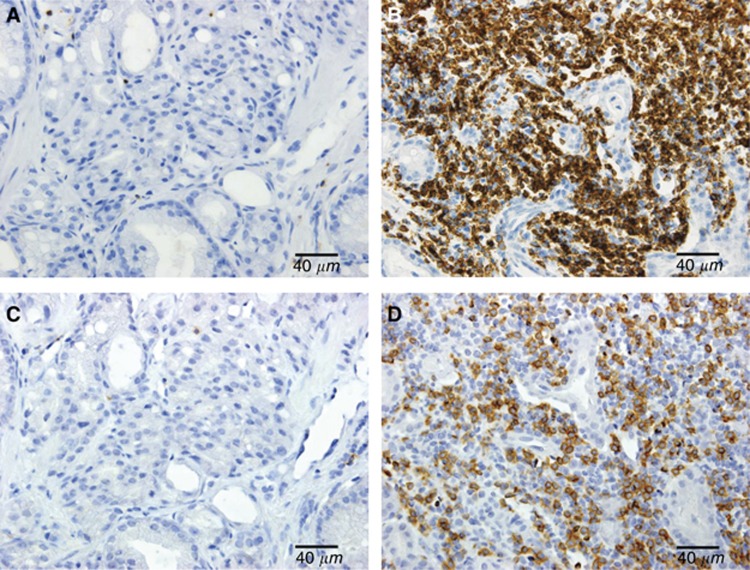
On the basis of our hypothesis and the prediction of the mathematical model, we retrieved tumour specimens from these patients and stained them for CD3 and CD8 as described in the Materials and Methods. Quantitation of CD3 and CD8 was performed blindly with respect to the presence/absence of a bounce in the PSA. The mean CD8 cell density per mm3 in tumours with and without a subsequent PSA bounce after brachytherapy were 70.92 and 38.55, respectively (F=5.9 × 10−5, P=0.035). In the case of CD3+ cells, the mean density in tumours with and without a subsequent bounce was 144.9 and 86.4, respectively (F test=3.05 × 10−5, P=0.05). Representative examples of CD3 and CD8 stains from tumours taken from patients that did/did not developed a PSA bounce are shown in Figure 3.

Figure 3.

Figure 3

Open in a new tab

Representative immunostaining analysis. CD3 (A and B) along with CD8 (C and D) staining in patients without PSA bounce (A and C) and with bounce (B and D).

Discussion

Interstitial brachytherapy is highly effective for localised adenocarcinoma of the prostate. Therapy is generally well tolerated and may be curative in a number of cases. The dynamics of response to therapy as determined by the reduction in PSA have been a source of considerable interest and although several studies have shown that the presence of a PSA bounce is associated with a better long-term outcome (Patel et al, 2004; Caloglu et al, 2011; Hinnen et al, 2012; Bernstein et al, 2013; Chira et al, 2013), the actual mechanism of the PSA bounce and why it may be associated with an improved outcome have proven to be elusive. Several studies have attempted to understand the mechanisms behind the bounce and its prognostic implications (Patel et al, 2004; Crook et al, 2007; Mitchell et al, 2008; Caloglu and Ciezki, 2009; Caloglu et al, 2011; Kirilova et al, 2011; Hinnen et al, 2012). Kirilova et al (2011), using 3D MR spectroscopic imaging, showed that the bounce is associated with an increase in metabolic activity within the prostate unrelated to residual malignancy and proposed an ‘inflammatory' process behind the PSA bounce. It is also generally agreed that the only parameter that correlates with the presence/absence of the PSA bounce is patient age – the bounce is observed more often in younger patients (as also observed in our cohort). In one small series of patients who had repeat prostate biopsy during such PSA bounces, all patients had residual tumour present more than a year after interstitial brachytherapy (Reed et al, 2003). Some studies have reported that the incidence of a PSA bounce was more frequent in patients who received a higher radiation activity per unit volume of prostate (Stock et al, 2003; Toledano et al, 2006), but this was not confirmed by others (Merrick et al, 2002). Note that in our cohort of patients, there was no difference in the average dose of radiation administered or the prostate volume for patients who did or did not develop a PSA bounce. Moreover, the bounce in PSA invariably occurs after the isotope has effectively decayed (Figure 2) and the radiation effect cannot by itself explain this phenomenon. It is also possible to show intuitively that a model with two equations that account for tumour growth, PSA production and the effect of radiation cannot explain the PSA bounce. Let us assume that there is no immune response. Therefore, y(t)=0 at all times. As a result, Equations (1a and 1b) of the model lose the last term and Equations (2a and 2b) do not exist anymore. Therefore, such a model only captures (i) tumour population growth, (ii) PSA production by the tumour cells, and (iii) the effect of radiation therapy on tumour growth and PSA production. It is easy to see that once the effect of radiation is over (s1=s=0), then the equations only capture exponential growth of the tumour and PSA production. Given that the PSA bounce almost always occurs when the effect of radiation on the tumour has disappeared, it will be impossible for a two equation model to capture the PSA bounce because such a model will not be able to fit the PSA data showing an initial increase in PSA followed by decay without any additional therapy. We also note that if one were to postulate that the subsequent drop in PSA after the initial rise is due to an advanced tumour losing its ability to produce PSA, this would be difficult to reconcile with the observation that the PSA bounce is associated with an improved outcome because we would expect that a more dedifferentiated tumour to behave more aggressively and be associated with an inferior outcome.

Using a combination of clinical data and a mathematical model, we developed a novel hypothesis to explain the PSA bounce after interstitial brachytherapy for localised prostate cancer and provide preliminary proof of its validity using a large cohort of patients.

Our results suggest that the PSA bounce is a consequence of oscillations in the tumour–immune cell dynamics. If the impact of the immune cells on the tumour is insignificant, then the oscillations will not be noticeable (hence no bounce) and after the effects of radiation wear off, the tumour will recur. One reason for the weak impact of the immune cells on the tumour may be a lower number of immune cells within the tumour at the start of therapy as found in patients by histological analysis and predicted by our mathematical model and data fitting. In addition, the bounce may be associated with an improved outcome and may be a sign of a significant anti-tumour immune response. Our hypothesis is further supported by the finding of a negative correlation between patient age and the value of β, which suggests that with aging, the number of tumour-infiltrating T cells decreases, and this would be associated with a lower incidence of the PSA bounce in older patients, as reported in the literature (Toledano et al, 2006; Caloglu and Ciezki, 2009).

Given that the cells were present before initiation of interstitial brachytherapy suggests that the tumour was possibly suppressing the cytotoxic activity of the cells and this suppression was reduced or eliminated after significant tumour cytoreduction from the radiation. The model would suggest that the delay in the PSA bounce is due to an initial reduction in the population of infiltrating T cells within the tumour because lymphocytes are very sensitive to radiation. We postulate that with sufficient isotope decay, T cells are again recruited to the tumour site and perhaps are able to kill more tumour cells leading to the PSA bounce and ultimately, the better outcome. Our model suggests that further studies are needed to understand the mechanisms of prostate cancer infiltration by T cells. Such studies may provide important insights into the dynamics of the PSA bounce but perhaps also inform on which patients are more likely to respond to monoclonal antibody therapy such as nivolumab (anti-PD-1). It is as yet unclear whether the presence of higher numbers of T cells within the tumour prior to definitive brachytherapy is associated with a better long-term outcome and our cohort of patients is not large enough to make any definite predictions. Such analysis will require a larger series of patients and with longer follow-up. However, our studies and modelling suggest that it may be important to look for tumour-infiltrating T cells at the time of diagnosis because they may allay fear of relapse if the PSA starts rising after a year of therapy.

In our modelling, we used PSA as the only measure of the tumour burden. Although this is likely a simplification given the heterogeneity that is being increasingly recognised within tumours, we believe that such an assumption is justified by restricting our analysis to patients with early stage tumours (T2N0M0) who have a low tumour burden. Moreover, we would expect that patients with more undifferentiated tumours, where the PSA is less likely to be representative of the tumour burden, would not do well. The fact that patients with a PSA bounce have better outcomes would argue against them having more aggressive, advanced disease.

In summary, our observations and modelling suggest that the PSA bounce observed after interstitial brachytherapy for prostate cancer is likely due to an immune response to the tumour. The bounce is due to a delayed immune attack against the tumour cells and likely explains the improved long-term outcome observed in patients who experience such a bounce.

Acknowledgments

This work is dedicated to the memory of Chetan P Offord.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on British Journal of Cancer website (http://www.nature.com/bjc)

Supplementary Material

Supplementary Material
Click here for additional data file. (31.8KB, pdf)

References

  1. Ash D, Flynn A, Battermann J, de Reijke T, Lavagnini P, Blank L Group EEUBGroup ER (2000) ESTRO/EAU/EORTC recommendations on permanent seed implantation for localized prostate cancer. Radiother Oncol 57(3): 315–321. [DOI] [PubMed] [Google Scholar]
  2. Bernstein MB, Ohri N, Hodge JW, Garg M, Bodner W, Kalnicki S, Dicker AP, Guha C (2013) Prostate-specific antigen bounce predicts for a favorable prognosis following brachytherapy: a meta-analysis. J Contemp Brachytherapy 5(4): 210–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bostancic C, Merrick GS, Butler WM, Wallner KE, Allen Z, Galbreath R, Lief J, Gutman SE (2007) Isotope and patient age predict for PSA spikes after permanent prostate brachytherapy. Int J Radiat Oncol Biol Phys 68(5): 1431–1437. [DOI] [PubMed] [Google Scholar]
  4. Caloglu M, Ciezki J (2009) Prostate-specific antigen bounce after prostate brachytherapy: review of a confusing phenomenon. Urology 74(6): 1183–1190. [DOI] [PubMed] [Google Scholar]
  5. Caloglu M, Ciezki JP, Reddy CA, Angermeier K, Ulchaker J, Chehade N, Altman A, Magi-Galuzzi C, Klein EA (2011) PSA bounce and biochemical failure after brachytherapy for prostate cancer: a study of 820 patients with a minimum of 3 years of follow-up. Int J Radiat Oncol 80(3): 735–741. [DOI] [PubMed] [Google Scholar]
  6. Chavez-Galan L, Arenas-Del Angel MC, Zenteno E, Chavez R, Lascurain R (2009) Cell death mechanisms induced by cytotoxic lymphocytes. Cell Mol Immunol 6(1): 15–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chira C, Taussky D, Gruszczynski N, Meissner A, Larrivee S, Carrier JF, Donath D, Delouya G (2013) Unusually high prostate-specific antigen bounce after prostate brachytherapy: Searching for etiologic factors. Brachytherapy 12(6): 603–607. [DOI] [PubMed] [Google Scholar]
  8. Ciezki JP, Reddy CA, Garcia J, Angermeier K, Ulchaker J, Mahadevan A, Chehade N, Altman A, Klein EA (2006) PSA kinetics after prostate brachytherapy: PSA bounce phenomenon and its implications for PSA doubling time. Int J Radiat Oncol Biol Phys 64(2): 512–517. [DOI] [PubMed] [Google Scholar]
  9. Clark WH (1991) Tumour progression and the nature of cancer. Br J Cancer 64(4): 631–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Critz FA, Williams WH, Benton JB, Levinson AK, Holladay CT, Holladay DA (2000) Prostate specific antigen bounce after radioactive seed implantation followed by external beam radiation for prostate cancer. J Urol 163(4): 1085–1089. [PubMed] [Google Scholar]
  11. Critz FA, Williams WH, Levinson AK, Benton JB, Schnell FJ, Holladay CT, Shrake PD (2003) Prostate specific antigen bounce after simultaneous irradiation for prostate cancer: the relationship to patient age. J Urol 170(5): 1864–1867. [DOI] [PubMed] [Google Scholar]
  12. Crook J, Gillan C, Yeung I, Austen L, McLean M, Lockwood G (2007) PSA kinetics and PSA bounce following permanent seed prostate brachytherapy. Int J Radiat Oncol Biol Phys 69(2): 426–433. [DOI] [PubMed] [Google Scholar]
  13. D'Amico AV, Whittington R, Malkowicz SB, Schultz D, Blank K, Broderick GA, Tomaszewski JE, Renshaw AA, Kaplan I, Beard CJ, Wein A (1998) Biochemical outcome after radical prostatectomy, external beam radiation therapy, or interstitial radiation therapy for clinically localized prostate cancer. JAMA 280(11): 969–974. [DOI] [PubMed] [Google Scholar]
  14. Fang Y (2011) Asymptotic equivalence between cross-validations and Akaike information criteria in mixed-effects models. Journal of Data Science 9: 15–21. [Google Scholar]
  15. Forys U, Waniewski J, Zhivkov P (2006) Anti-tumor immunity and tumor anti-immunity in a mathematical model of tumor immunotherapy. Journal of Biological Systems 14(1): 13–30. [Google Scholar]
  16. Grivennikov SI, Greten FR, Karin M (2010) Immunity, inflammation, and cancer. Cell 140(6): 883–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hinnen KA, Monninkhof EM, Battermann JJ, van Roermund JG, Frank SJ, van Vulpen M (2012) Prostate specific antigen bounce is related to overall survival in prostate brachytherapy. Int J Radiat Oncol Biol Phys 82(2): 883–888. [DOI] [PubMed] [Google Scholar]
  18. Horwitz EM, Levy LB, Thames HD, Kupelian PA, Martinez AA, Michalski JM, Pisansky TM, Sandler HM, Shipley WU, Zelefsky MJ, Zietman AL, Kuban DA (2006) Biochemical and clinical significance of the posttreatment prostate-specific antigen bounce for prostate cancer patients treated with external beam radiation therapy alone: a multiinstitutional pooled analysis. Cancer 107(7): 1496–1502. [DOI] [PubMed] [Google Scholar]
  19. Hurvich CM, Tsai CL (1989) Regression and time series model selection in small samples. Biometrika 76(2): 297–307. [Google Scholar]
  20. Kirilova A, Damyanovich A, Crook J, Jezioranski J, Wallace K, Pintilie M (2011) 3D MR-spectroscopic imaging assessment of metabolic activity in the prostate during the PSA ‘bounce' following 125iodine brachytherapy. Int J Radiat Oncol Biol Phys 79(2): 371–378. [DOI] [PubMed] [Google Scholar]
  21. Kuznetsov VA, Makalkin IA, Taylor MA, Perelson AS (1994) Nonlinear dynamics of immunogenic tumors: parameter estimation and global bifurcation analysis. Bull Math Biol 56(2): 295–321. [DOI] [PubMed] [Google Scholar]
  22. Merrick GS, Butler WM, Wallner KE, Galbreath RW, Anderson RL (2002) Prostate-specific antigen spikes after permanent prostate brachytherapy. Int J Radiat Oncol Biol Phys 54(2): 450–456. [DOI] [PubMed] [Google Scholar]
  23. Mitchell DM, Swindell R, Elliott T, Wylie JP, Taylor CM, Logue JP (2008) Analysis of prostate-specific antigen bounce after I(125) permanent seed implant for localised prostate cancer. Radiother Oncol 88(1): 102–107. [DOI] [PubMed] [Google Scholar]
  24. Nakano O, Sato M, Naito Y, Suzuki K, Orikasa S, Aizawa M, Suzuki Y, Shintaku I, Nagura H, Ohtani H (2001) Proliferative activity of intratumoral CD8(+) T-lymphocytes as a prognostic factor in human renal cell carcinoma: clinicopathologic demonstration of antitumor immunity. Cancer Res 61(13): 5132–5136. [PubMed] [Google Scholar]
  25. Offord C, Bajzer Z (2006) A hybrid global optimization algorithm involving simplex and inductive search. Lecture Notes Comput Sci 2074: 680–688. [Google Scholar]
  26. Patel C, Elshaikh MA, Angermeier K, Ulchaker J, Klein EA, Chehade N, Wilkinson DA, Reddy CA, Ciezki JP (2004) PSA bounce predicts early success in patients with permanent iodine-125 prostate implant. Urology 63(1): 110–113. [DOI] [PubMed] [Google Scholar]
  27. Prestigiacomo AF, Stamey TA (1996) Physiological variation of serum prostate specific antigen in the 4.0 to 10.0 ng./ml. range in male volunteers. J Urol 155(6): 1977–1980. [PubMed] [Google Scholar]
  28. Reed D, Wallner K, Merrick G, Buskirk S, True L (2003) Clinical correlates to PSA spikes and positive repeat biopsies after prostate brachytherapy. Urology 62(4): 683–688. [DOI] [PubMed] [Google Scholar]
  29. Schietinger A, Delrow JJ, Basom RS, Blattman JN, Greenberg PD (2012) Rescued tolerant CD8 T cells are preprogrammed to reestablish the tolerant state. Science 335(6069): 723–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schietinger A, Greenberg PD (2014) Tolerance and exhaustion: defining mechanisms of T cell dysfunction. Trends Immunol 35(2): 51–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sharma P, Shen Y, Wen S, Yamada S, Jungbluth AA, Gnjatic S, Bajorin DF, Reuter VE, Herr H, Old LJ, Sato E (2007) CD8 tumor-infiltrating lymphocytes are predictive of survival in muscle-invasive urothelial carcinoma. Proc Natl Acad Sci USA 104(10): 3967–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Stamey TA, Yang N, Hay AR, McNeal JE, Freiha FS, Redwine E (1987) Prostate-specific antigen as a serum marker for adenocarcinoma of the prostate. N Engl J Med 317(15): 909–916. [DOI] [PubMed] [Google Scholar]
  33. Stepanova N (1980) Course of the immune reaction during the development of a malignant tumor. Biophysics 24: 917–923. [Google Scholar]
  34. Stock RG, Stone NN, Cesaretti JA (2003) Prostate-specific antigen bounce after prostate seed implantation for localized prostate cancer: descriptions and implications. Int J Radiat Oncol Biol Phys 56(2): 448–453. [DOI] [PubMed] [Google Scholar]
  35. Stock RG, Stone NN, Wesson MF, DeWyngaert JK (1995) A modified technique allowing interactive ultrasound-guided three-dimensional transperineal prostate implantation. Int J Radiat Oncol Biol Phys 32(1): 219–225. [DOI] [PubMed] [Google Scholar]
  36. Toledano A, Chauveinc L, Flam T, Thiounn N, Solignac S, Timbert M, Rosenwald JC, Cosset JM (2006) PSA bounce after permanent implant prostate brachytherapy may mimic a biochemical failure: a study of 295 patients with a minimum 3-year followup. Brachytherapy 5(2): 122–126. [DOI] [PubMed] [Google Scholar]
  37. Wallner KE BJ, Dattoli MJ (1997) Prostate Brachytherapy Made Complicated Vol. 14. SmartMedicine: Seattle, WA, USA. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
Click here for additional data file. (31.8KB, pdf)

Articles from British Journal of Cancer are provided here courtesy of Cancer Research UK

RESOURCES