Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Feb 9;120(27):4884–4892. doi: 10.1021/acs.jpca.5b12450

Three-Dimensional Model for Electrospinning Processes in Controlled Gas Counterflow

Marco Lauricella †, Dario Pisignano ‡,§, Sauro Succi †,∥,*
PMCID: PMC4947972  PMID: 26859532

Abstract

graphic file with name jp-2015-12450t_0010.jpg

We study the effects of a controlled gas flow on the dynamics of electrified jets in the electrospinning process. The main idea is to model the air drag effects of the gas flow by using a nonlinear Langevin-like approach. The model is employed to investigate the dynamics of electrified polymer jets at different conditions of air drag force, showing that a controlled gas counterflow can lead to a decrease of the average diameter of electrospun fibers, and potentially to an improvement of the quality of electrospun products. We probe the influence of air drag effects on the bending instabilities of the jet and on its angular fluctuations during the process. The insights provided by this study might prove useful for the design of future electrospinning experiments and polymer nanofiber materials.

1. Introduction

The production of nano- and microfibers has gained increasing interest due to the large number of promising applications, including filtration, textiles, medical, protective, structural, electrical, and optical materials and coatings. In particular, an intriguing feature of electrospun fibers is the high surface-area, which is due to the combination of small radius and extreme length of the fiber (in principle up to kilometers when polymer solutions with a high degree of molecular entanglement are used to achieve stable electrified jets). This offers intriguing perspectives for practical applications. As a consequence, several studies have been focused on the production and characterization of such structures.1−7

Following the pioneering works of Rayleigh8 and, later, Zeleny,9 the electrospinning process relies on a strong electric field (typically 105–106 V·m–1) to elongate and accelerate a polymeric fluid body from a nozzle toward a conductive collector. During the development of the jet path, the stream cross-section decreases by orders of magnitude, providing a jet, and consequently solid fibers, with transversal size potentially well below the micrometer scale. The dynamic evolution of the polymer nanojet involves two different stages: in the first, the pendent polymeric droplet is stretched by the intense external electric field, providing a straight path. In the second, small perturbations induce bending instabilities, and a complex jet path is consequently observed. In a typical electrospinning experiment, hydrodynamic perturbations, as well as mechanical vibrations nearby the nozzle, might misalign the jet axis. According to the Earnshaw theorem,10 an off-axis misalignment triggers an electrostatic-driven bending instability, leading the fluid into a region of spiral coils. As a consequence, the jet travels a larger distance between the nozzle and the collector, and the fiber diameter undergoes a further decrease along the way, leading to a reduction of the fiber diameter.

Several studies were focused on experimental parameters, such as applied electric voltage, liquid viscosity, etc.11−14 Similarly, the use of complementary external forces was also investigated. For instance, a gas stream provided by suitable distributers and surrounding the electrospinning nozzle can be used as additional stretching force, providing fibers with small diameter.15−20 This process is generally called gas-assisted electrospinning (sometimes electroblowing). Nonetheless, many of the effects of gas flows on electrospinning still need to be investigated in a systematic way, particularly with regard to the relationship between gas flow speed and bending instabilities. Indeed, given the ubiquitous nature of intentional or stochastic gas flows in the process atmosphere, understanding in depth such points is very important for a correct design of electrospinning experiments, when fibers with very small diameters are to be produced with a given polymer solution.

In this framework, simulation models can be useful for understanding the key processing parameters and ultimately exerting a better control on the resulting fiber morphologies, better elucidating the phenomenology of electrified jets and providing valuable information for the development of new spinning experiments. For these reasons, various models have been proposed for electrospinning in the recent years,12,13,21−24 which can be categorized on the basis of the approach used for representing the jet. In the first class of models, the filament is treated as obeying the equations of continuum mechanics,23,25−28 whereas in the second the jet is described as a series of discrete elements obeying the equations of Newtonian mechanics,21,22 as it is the case of the present work.

Recently, Lauricella et al.29 developed a one-dimensional model for studying the air drag effects on the early stage of electrospinning process. In this approach, the liquid jet was represented as a series of charged beads, connected by viscoelastic springs according to the original picture proposed by Reneker and Yarin.21,22 The jet dynamics was the result of the combined action of viscoelastic Coulombic, external electrical forces, and a dissipative term that models the air drag effect. On the basis of experimental observations,30 the dissipative air drag term was taken as nonlineary dependent on the jet geometry. As consequence, the model included a nonlinear Langevin-like stochastic differential equation describing the fluid motion. However, an investigation of the air drag effects on three-dimensional (3D) bending instabilities was still missing.

Here, we provide a 3D description of electrified jets which includes air drag, and study its effects in the dynamics of the bending instabilities. In particular, our aim is to investigate the relation between the dissipative-perturbing forces and the resulting deposition of electrospun fibers. Furthermore, the extended model is used to set up an ideal experiment of gas-assisted electrospinning, which involves a gas-injecting system located at the collector and oriented toward the spinneret. In this context, we probe the effects of a controlled gas counterflow on the fiber diameter, which could be useful for designing new electrospinning experiments.

The article is organized as follows. In section 2, we present the 3D model for electrospinning, with the set of stochastic differential equations of motion (EOM) that govern the dynamics of system. Results are reported and discussed in section 3. Finally, conclusions are outlined in section 4.

2. Model of Electrospinning in a Gas Flow

In this paper, we modify the 3D model of electrospinning previously implemented in the software package JETSPIN, a specifically developed, open-source and freely available code.31,32 We use a Lagrangian discrete model that represents the polymer solution filament as a series of n beads (jet beads) at mutual distance l, each pair of beads in the row being connected by viscoelastic elements, as proposed in ref (21) (Figure 1). The length l is taken to be larger than the radius of the filament. Each ith bead has mass mi and charge qi, assumed equal for all the beads for simplicity. The spinneret is represented by a single mass-less point of charge q0 fixed at x = 0, which we call the nozzle bead. A typical simulation is started with a single jet bead inserted at the nozzle and placed at a distance lstep from the nozzle along the x axis. The onset of the jet takes place with a cross-sectional radius a0, defined as the radius of the polymer solution filament at the nozzle, before the stretching process occurs, leading to the elongation and cross-section reduction in the fluid body. Furthermore, the starting jet bead has an initial velocity vs along the x axis equal to the bulk fluid velocity in the needle of the extrusion syringe or reservoir. Once this traveling bead reaches a distance 2·lstep away from the nozzle, a new particle (third body) is placed at distance lstep from the nozzle along the straight line joining the two previous bodies (nozzle and previous jet bead). Note that lstep defines the length step used to discretize the liquid jet at the nozzle before the stretching process starts taking place. The procedure is then repeated, leading to a series of n beads representing the jet. It is worth stressing that hereafter we indicate by i = 1 the particle which is the closest to the collector.

Figure 1.

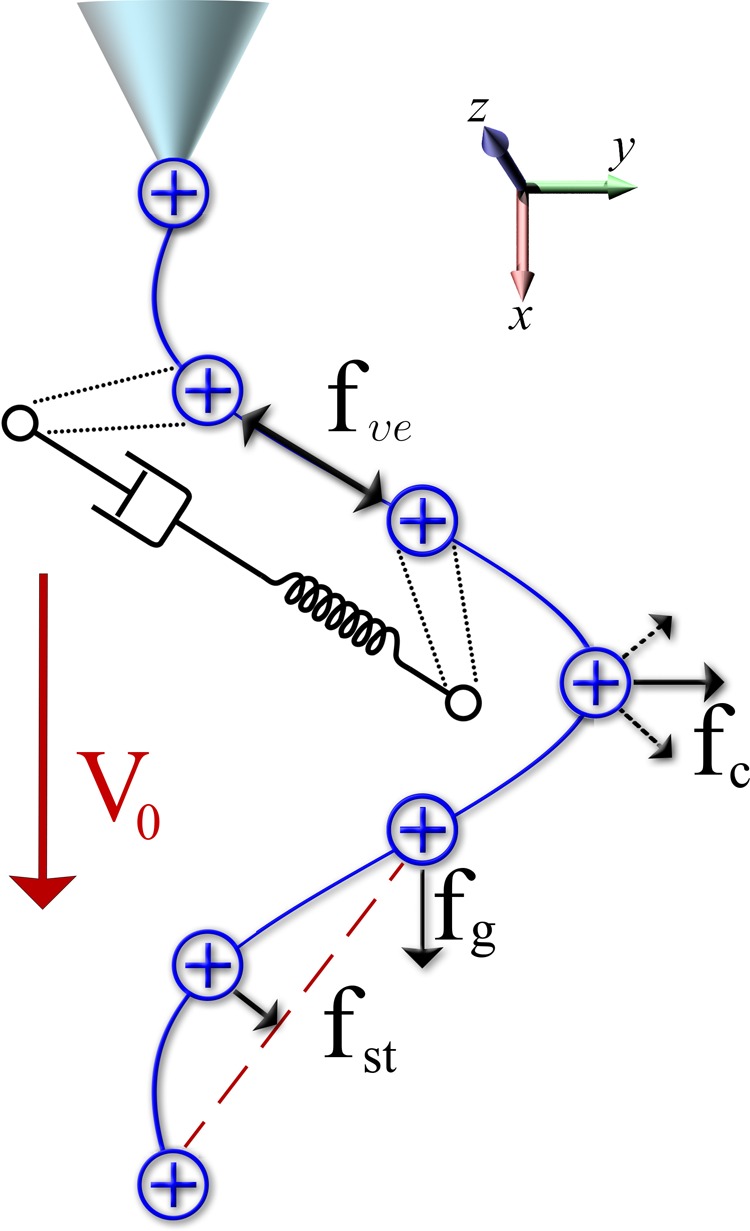
Figure 1

Open in a new tab

Diagram of the electrospinning model as implemented in the “vanilla” version of JETSPIN without air drag and lift force terms (which are sketched in Figure 2). Each discrete element representing a jet segment is drawn by a blue circle with a plus sign denoting the positive charge of segment. We represent the Maxwell viscoelastic force, fve, the gravitational force f⃗g, the surface tension force, fst, pointing to the center of curvature to restore the rectilinear shape, and the Coulomb repulsive term, fc, which is the sum over all the repulsive interactions between the beads. The external electric potential, V0, is indicated by the red arrow in figure, and the upper cyan cone represents the nozzle. The dashed red line represents the ideal straight line to which the filament tends under the surface tension force.

The jet is therefore modeled as a body constituted by a viscoelastic Maxwell fluid, and the stress σi on the ith dumbbell which connects the bead i with the bead i + 1 is given by the equation

2. 1

where li is the length of the element, G is the elastic modulus, μ the viscosity of the fluid jet, and t is the time (Figure 1). The length li is computed as the mutual distance between the ith bead and its previous bead. Being ai the fiber radius at the bead i, the viscoelastic force, f⃗ve, pulling the bead i back to i – 1 and toward i + 1, reads as follows:

2. 2

where t⃗i is the unit vector pointing from bead i – 1 to bead i. The force f⃗st due to the surface tension for the ith bead is given by

2. 3

where α is the surface tension coefficient, ki is the local curvature, and c⃗i is the unit vector pointing the center of the local curvature from bead i (Figure 1). The force f⃗st tends to restore the rectilinear shape acting on the bent part of the jet.

In electrospinning processes, the jet stretch is mainly due to an external electric potential V0 that is applied between the spinneret and the conducting collector. Denoted by h, the distance of the collector from the injection point, each ith bead undergoes the electric force:

2. 4

where x⃗ is the unit vector pointing the collector from the spinneret (Figure 1). Note that whenever a jet bead touches the collector, its position is frozen and its charge is set to zero.

The net Coulomb force f⃗c on the ith bead from all the other beads is given by

2. 5

where Rij2 = (xi – xj)2 + (yi – yj)2 + (zi – zj)2, and u⃗ij is the unit vector pointing the ith bead from the jth bead.

The force due to the gravity is also considered in the model, and it is computed by the usual expression

2. 6

where g is the gravitational acceleration.

These features are implemented in the JETSPIN software package.31 Next, we extend the 3D framework to include the air drag terms and reproduce aerodynamic effects. Consequently, code modifications have been implemented in JETSPIN. In particular, we model the air drag by adding a random term and a dissipative term to the forces involved in the process. The dissipative air drag term is usually dependent on the geometry of the jet, which changes in time, and it combines longitudinal and lateral components. On the basis of experimental findings,30,33,34 the longitudinal component of the air drag dissipative force term acting on a jet segment of length l is given by the empirical formula

2. 7

where ρa denotes the air density, νa the kinematic viscosity, t⃗ the tangent unit vector, and vt = (v⃗ – v⃗flow)·t⃗ represents the tangent component of the total velocity with respect to the air flow given as the difference between jet velocity v and air flow velocity vflow. The gas flow is assumed to be oriented along the x-axis with opposite direction, but the choice is not mandatory. Following the approach introduced by Lauricella et al.,29 we rearrange the last eq as

2. 8

Rewriting eq 8 for the ith bead representing a jet segment, and assuming a constant volume of the jet πai2li = πa02lstep, so that

2. 9

with lstep and a0 respectively the length and the radius of the jet segment at the nozzle before the stretching, we obtain

2. 10

where we have collected several terms of the empirical relationship in γi which is equal to

2. 11

to obtain the dissipation term of a non linear Langevin-like equation (for further details see Lauricella et al.29). It is worth stressing that γi is derived by the empirical relationship of eq 7, so that also eq 11 is a nondimensional combination of physical parameters.

In a 3D framework a lateral lift force should also be considered. Following the expression introduced by Yarin,34,35 under a high-speed air drag the lateral component f⃗lift,i of the aerodynamic dissipative force related to the flow speed is given in the linear approximation (for small bending perturbations) by

2. 12

The combined action of such longitudinal and lateral components (Figure 2) provide the dissipative force term acting on the ith bead

2. 13

whereas the random force term for the ith bead has the form

2. 14

where Dv denotes a generic diffusion coefficient in velocity space (which is assumed constant and equal for all the beads), and η⃗i is a 3D vector, whereof each component η is an independent stochastic process, namely, a nowhere differentiable function with ⟨η(t1) η(t2)⟩ = δ(|t2 – t1|)s, and ⟨η(t)⟩ = 0. Note that, for the sake of simplicity, we assume η = dς(t)/dt, where ς(t) is a Wiener process, namely, a stochastic processes with stationary independent increments (often called standard Brownian motion).36

Figure 2.

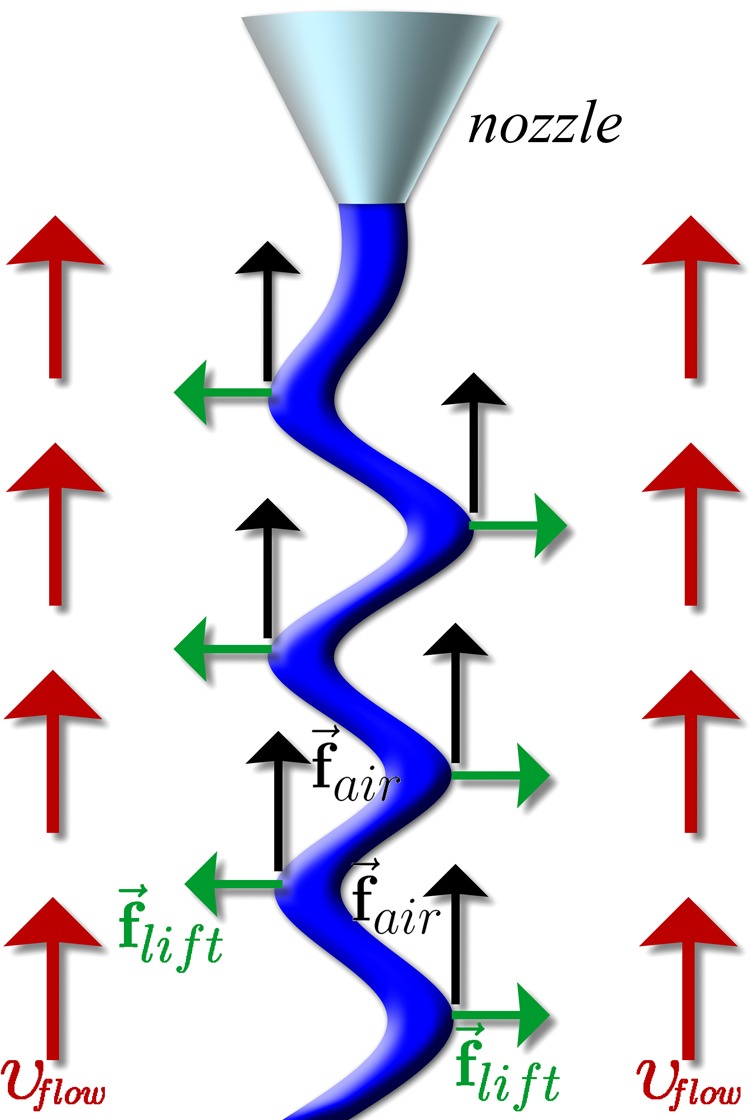
Figure 2

Open in a new tab

Diagram of the electrospinning model showing the dissipative force, which is the sum of air drag force, f⃗air (black arrows) and lift force, f⃗lift (green arrows), when a gas flow of speed vflow is present (red arrows).

The sum of these forces governs the jet dynamics according to the Newton’s equation providing the following nonlinear Langevin-like stochastic differential equation:

2. 15

where v⃗i is the velocity of the ith bead. The velocity v⃗i satisfies the kinematic relation:

2. 16

where r⃗i(xi,yi,zi) is the position vector of the ith bead. Equations 1, 15, and 16 form the set of EOM governing the time evolution of the system. It is worth noting that eq 15 recovers a deterministic EOM in the limit ρa and Dv → 0.

Furthermore, we define also the EOM of the nozzle bead located to model fast mechanical perturbations at the spinneret.21,37 Given the initial position of the nozzle yn0 = A·cos(φ) and zn = A·sin(φ) where A and φ are the amplitude and the initial phase of the perturbation, respectively, the EOM for the nozzle bead are

2. 17a
2. 17b

where ω denotes the perturbation frequency. The actual perturbation at the nozzle produces a characteristic annular deposition of the fiber on the collector, as initially observed by Reneker et al.21 Altough the collected fibers observed in experimental findings show less regular fiber patterns, we find it convenient to investigate counterflow effects avoiding extra perturbations not directly related to the gaseous counterflow. Thus, we focus our investigation on the specific perturbation effect due to a counterflow gas on the jet dynamics.

Following previous works,29,38 the EOM are integrated as follows. First, the time is discretized as a uniform sequence ti = t0 + jΔt, j = 1, ..., nsteps. At each time step and for each ith jet bead, we first integrate the stochastic eq 15 using the explicit integration scheme proposed by Platen,39,40 with the order of accuracy evaluated in the literature equal to 1.5. Then, eqs 16 and 1 are integrated via second-order Runge–Kutta integrator, where the v⃗i(t+Δt) value was previously obtained via the Platen scheme.

3. Results and Discussion

3.1. Simulations Setup for PVP Electrified Jets

Solutions of polyvinylpyrrolidone (PVP) are largely used in electrospinning experiments. In this work, we use a few simulation parameters developed by Lauricella et al.31 and based on the experimental data provided by Montinaro et al.14 The process makes use of a solution of PVP (molecular weight = 1300 kDa) prepared by a mixture of ethanol and water (17:3 v:v), at a concentration ranging between 11 and 21 mg/mL. The relevant parameters include mass, charge density, viscosity, elastic modulus, and surface tension, which were already included in the model as implemented in JETSPIN.31 The extra parameters related to the gas environment are modeled on the air (density ρa = 1.21 kg/m3, kinematic viscosity νa = 0.151 cm2/s). The parameter Dv,i for the ith bead is set to be γi for all the simulations. All the γi have the same value, and consequently, Dv,i is constant for all the beads. In addition, a perturbation is applied at the nozzle with frequency ω = 104s–1, as proposed by Reneker et al.,21 whereas its amplitude A is equal to 0.01 mm. The voltage bias between the nozzle and the collector is 9 kV, and the collector is placed at 16 cm from the nozzle. The initial fluid velocity vs was estimated considering a solution pumped at constant flow rate of 2 mL/h in a needle of radius 250 μm. For convenience, all the simulation parameters are summarized in Table 1. We probe three different conditions of air flow velocity, vflow. In the first, we study the electrospinning process in the absence of gas flow, vflow = 0, which will be use as a reference case (case I). In the second and third, we take vflow = −10 m/s (case II), and vflow = −20 m/s (case III), whose magnitudes are similar to the jet velocity measured at the collector (about 20 m/s) in the absence of gas streams. It is worth stressing that the gas flow is oriented along the x-axis, and the negative sign of vflow indicates its opposite direction (counterflow, from the collector toward the nozzle). For each of the three conditions, we run ten independent trajectories to perform a statistical analysis. All simulations were carried out by the modified version of the software package JETSPIN,31 and the corresponding EOM were integrated with a time step of 10–9 seconds over a simulation span of 0.5 s.

Table 1. Simulation Parameters for the Simulations of Electrified Jets by PVP Solutionsa.

ρ (kg/m3) ρq (C/L) a0 (cm) vs (cm/s) α (N/m) μ (Pa·s)
840 2.8 × 10–7 5 × 10–3 0.28 2.11 × 10–2 2.0
G (Pa) V0 (kV) ω (s–1) A (cm) ρa (kg/m3) νa (cm2/s)
5 × 104 9.0 104 10–3 1.21 0.151
Open in a new tab
a

The headings used are as follows: ρ, density; ρq, charge density; a0, fiber radius at the nozzle; vs, initial fluid velocity at the nozzle; α, surface tension; μ, viscosity; G, elastic modulus; V0, applied voltage bias; ω, frequency of perturbation; A, amplitude of perturbation; ρa, air density; νa, air kinematic viscosity.

For the sake of convenience, we report below the definition of few observables, which will be used in the following. We define the jet length as

3.1. 18

with r⃗i the position vector, and n the number of jet beads. This observable takes note of the total length of the jet from the collector up to the nozzle. Further, we introduce a suitable observable to assess the tortuosity of the path, which is defined as

3.1. 19

where |r⃗1|is the position vector modulus of the closest bead to the collector. Note that Λ tends to 1 for a rectilinear jet, and it takes larger values depending on the complexity of the bending part of the jet. We also define the instantaneous angular aperture of the instability cone as

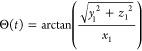3.1. 20

with x1, y1 and z1 the coordinates of the bead closest to the collector (Figure 1).

In all the simulations, we observed two different regimes of the observables (λ, Λ, Θ, etc.) describing the process. In the first stage, the jet has not yet reached the collector, and we observe an initial transient of the observables. After the jet touches the collector, the observables start to fluctuate around a constant mean value, providing a stationary regime. As a consequence, we discern two stages of the jet dynamics, hereafter denoted as early and late dynamics, respectively.

3.2. Early Dynamics

For each case, we compute the average values of observables describing the jet dynamics (Figure 3). The averages are assessed at every step of the time integration; hence, we obtain time-dependent mean values of observables along the jet evolution. In Table 2 we report the average first-hitting-time, ⟨tfirst⟩, defined as the time that the jet initially takes to touch the collector. In particular, we note that the presence of a gas counterflow does not affect significantly the first-hitting-time, and the velocity of the jet bead at the collector is almost the same for all the three investigated cases (within the margin of error). For the sake of completeness, we plot in Figure 4 the time-dependent mean velocity of the first bead as a function of time. On the contrary, a significant increase of the jet length ⟨λ(tfirst)⟩ is found upon increasing the gas counterflow speed vflow. This effect might be relevant for improving the quality of the resulting fibers, because longer jet lengths usually correspond to smaller cross sections of the deposited polymer filaments. Such an increment of ⟨λ(tfirst)⟩ is due to the greater complexity of the jet path, where bending instabilities play a significant role in determining the distance traveled from the nozzle to the collector. This is well represented by the Λ parameter, which increases by 20% in case III, when the gas flow is set to vspeed = −20 m/s.

Figure 3.

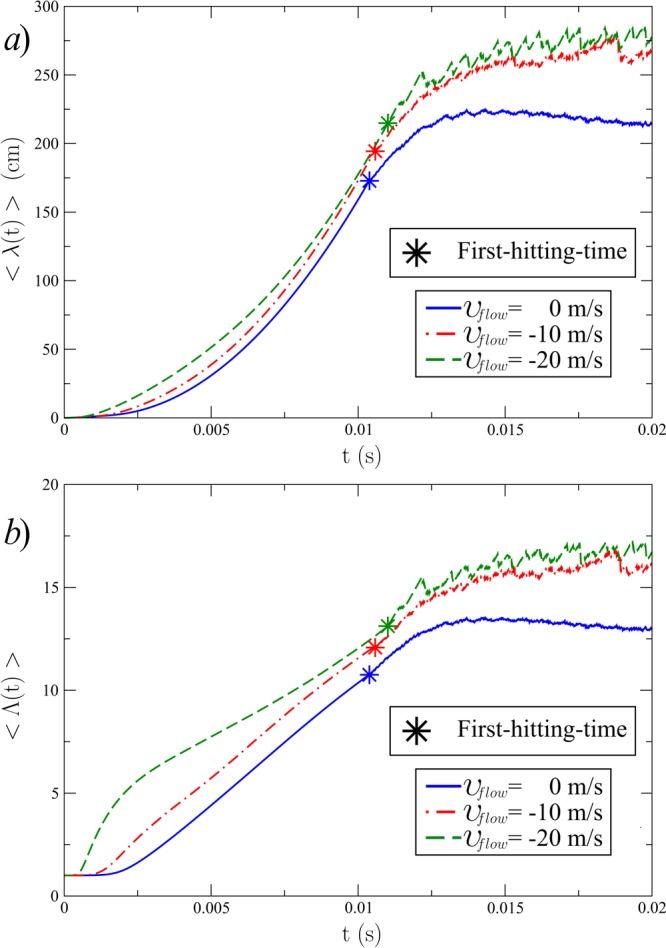
Figure 3

Open in a new tab

Time-dependent mean values of the observables jet length, ⟨λ(t)⟩ (a) and tortuosity degree, ⟨Λ(t)⟩ (b) for the different cases of flow speed vflow. Stars: times corresponding to the mean value of the first-hitting-time, ⟨tfirst⟩, for each case.

Table 2. Mean Values of the Observables First-Hitting-Time tfirst, and Mean Values of the Following Observables at the First-Hitting-Time: Jet Velocity Measured at the Collector vjet(tfirst), Jet Path Length λ(tfirst), and Tortuosity Degree Parameter Λ(tfirst)a.

  case I case II case III
observables vflow = 0 m/s vflow = −10 m/s vflow = −20 m/s
⟨tfirst⟩ (s) 1.0385 × 10–2 ± 8 × 10–6 1.058 × 10–2 ± 1 × 10–5 1.101 × 10–2 ± 2 × 10–5
⟨vjet(tfirst)⟩ (m/s) 19.6 ± 0.2 19.3 ± 0.3 19.5 ± 0.4
⟨λ(tfirst)⟩ (cm) 172.8 ± 0.2 194.4 ± 0.7 214.8 ± 0.8
⟨Λ(tfirst)⟩ 10.8 ± 0.1 12.1 ± 0.3 13.1 ± 0.4
Open in a new tab
a

The averages were computed over all the ten trajectories for each of the three cases of gas flow speed vflow. We report also the error as standard deviation of distribution.

Figure 4.

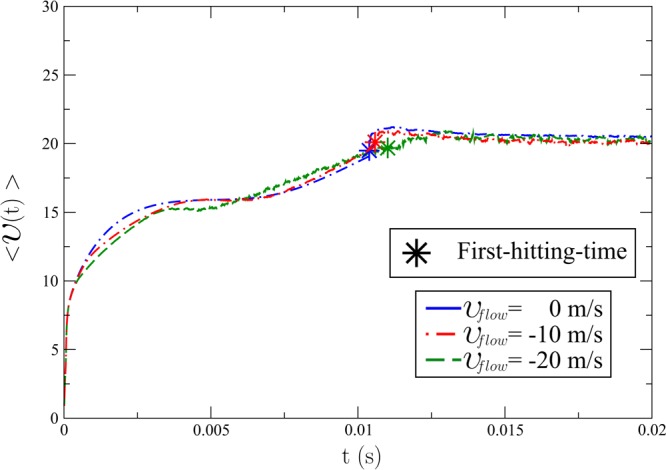
Figure 4

Open in a new tab

Time-dependent mean value of the jet velocity ⟨v(t)⟩ (meter per second) as a function of time (second) for all the three cases. Stars: times corresponding to the mean value of the first-hitting-time, ⟨tfirst⟩, for each case.

The dynamics of bending instabilities also deserves a few comments: we show in Figure 4 the time-dependent mean value of the jet length, ⟨λ(t⟩⟩, and tortuosity degree, ⟨Λ(t)⟩, for each case under investigation. Here, we find that bending instabilities start earlier for case III, triggering a larger jet path in the subsequent dynamics. This is well represented by the initial hump of ⟨Λ(t)⟩, which is already equal to 5.0 after 0.002 s. The larger tortuosity degree is likely due to the lift force, which increases the local curvature of the jet, as shown in eq 12. Hence, the synergic action of lift and Coulomb repulsive forces boost bending instabilities at an earlier stage, and case III shows a different dynamics, which is clearly evident in the initial 0.005 s. This effect substantially differs from what is reported in literature for electrospinning models without external gas flows, where only Coulomb repulsive forces contribute to the jet misalignement.21

Furthermore, we note that ⟨λ(t)⟩ increases for all the cases both before and after the jet has touched the collector for the first time, indicating that bending instabilities reach a stationary regime of fluctuation at least after the time tlim ≈ 2·⟨tfirst⟩. We will consider this criteria in the following subsection, to discard the initial transient of dynamics for a correct statistical analysis of the stationary regime.

3.3. Late Dynamics

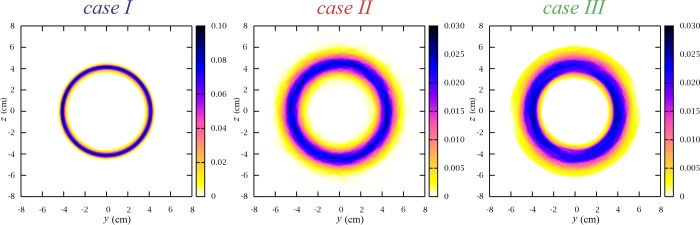
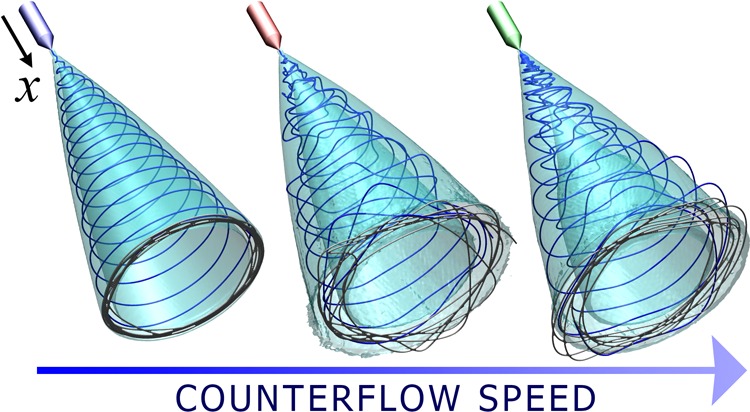
We perform a statistical analysis of the positions of the jet beads over all the ten independent simulations for each of the three cases under investigation. In particular, we define an orthogonal box of dimensions 16 cm × 8 cm × 8 cm along the x, y, and z-axes, respectively. The orthogonal box is discretized in subcubic cells of side equal to 1 mm, and the normalized numerical density field, denoted ρ̃i,j,k, is computed over all the box for each case. By construction, ρ̃i,j,k provides the probability to find a jet bead in the cubic cell identified by the indices i, j, k. As above, we discard the initial part of each simulation, which corresponds to the early dynamics, so that only the late dynamics describing the stationary regime is considered. Hence, the dynamics of each trajectory is evolved in time for 0.5 s. Figure 5 displays the isosurface of ρn representing points of constant value 0.001. The jet paths statistically lie on an empty cone, whose aperture slightly increases upon increasing the flow speed vflow. In addition, the chaotic behavior of jets is found to be enhanced by high-speed gas flows. This is shown both by the larger statistical dispersion of the cone (thickness of cone wall) and by the different shape of the electrospun coatings deposited on the collector, which follow a fuzzier path (gray fiber drawn in Figure 5). The different depositions of fibers for the three cases are highlighted by the normalized 2D maps in Figure 6, where we show the probability of a jet bead hitting the collector at the coordinates y and z (note that the plate is perpendicular to x by construction). Here, all the distributions are found to draw almost regular circles, which subtend their relative instability cones of aperture angle Θ. The probability distribution of hitting a specific point on the collector is remarkably peaked in case I without gas flow, whereas the fiber deposition becomes less regular in the other cases. In particular, the distributions lie within two concentric circles, whose inner radius decreases, while the outer increases, as the air gas flow is enforced. The trend is a consequence of the more complex paths with highest tortuosity degree Λ (see case III in Table 3) drawn by the jets under the effects of strong perturbation forces in the presence of a high speed gas counterflow. The snapshot related to case III in Figure 5 represents well the chaotic route followed by the viscoelastic jet under the gas flow effects, which provides a longer jet path length λ, whose mean value ⟨λ⟩ increases by increasing the flow speed vflow, as reported in Table 3. On the contrary, the mean values of the aperture angle Θ are not significantly altered by the gas flow (Table 3), showing that the instability mainly alters the statistical dispersion of the cone, but not in its mean value.

Figure 5.

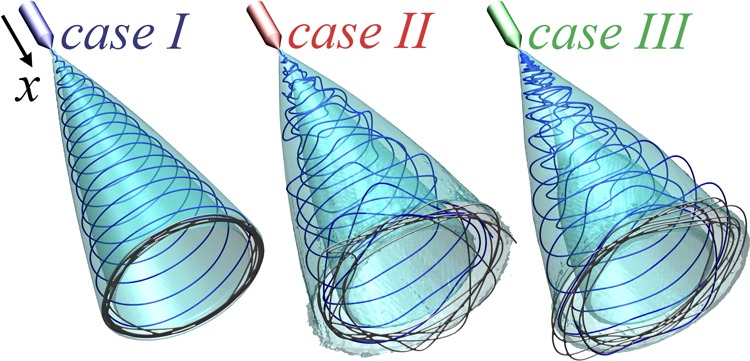
Figure 5

Open in a new tab

Simulation snapshots of the three different cases. From left to right the snapshots correspond to case I, vflow = 0 m/s, case II, vflow = −10 m/s, and case III, vflow = −20 m/s, respectively. The jet between the nozzle and the collector is drawn in blue, and the fibers deposited on the collector are gray. The isosurfaces in cyan represent the normalized numerical density field ρ̃ of constant value equal to 0.001.

Figure 6.

Figure 6

Open in a new tab

Normalized 2D maps computed over the coordinates y and z of the collector for the three cases under investigation. The color palettes define the probability that a jet bead hits the collector in coordinates y and z.

Table 3. Mean Values of the Observables: Aperture Angle of Instability Cone Θ, Jet Path Length λ, and Tortuosity Degree Parameter Λa.

  case I case II case III
observables vflow = 0 m/s vflow = −10 m/s vflow = −20 m/s
⟨Θ⟩ (deg) 28.1 ± 1.2 30.1 ± 2.8 29.6 ± 2.9
⟨λ⟩ (cm) 213.8 ± 2.2 266 ± 12 279 ± 13
⟨Λ⟩ 13.4 ± 0.1 16.7 ± 0.8 17.5 ± 0.9
Open in a new tab
a

The averages were computed only in the stationary regime over all the ten trajectories for each of the three cases of gas flow speed vflow. We report also the error as standard deviation of distribution.

The high-speed gas flow significantly affects the size distribution of the deposited fibers. In Figure 7 we report the probability of collecting fibers with a given value of cross-sectional radius. Here, we observe a nontrivial trend of the fiber radius as a function of the air counterflow velocity. In particular, by applying an air flow velocity vflow of −10 m/s (case II), we note a decrease in fiber radius by 10%–15%, and the fiber radius probability distributions become broader. The latter effect is even more evident for case III (vflow = −20 m/s), where the distribution computed over all the trajectories is spread out from its mean with values of fiber radius oscillating between 3 and 8 μm. Further, we observe a nonsymmetric distribution of the fiber radius for both cases II and III, which may appear somehow counterintuitive. Nonetheless, we point out that skewed probability distributions are quite common in the statistical behavior of complex nonlinear systems, such as the one considered here. Fluid turbulence is a typical example in point.41,42 Although finding the coarse-grained dynamic equations of motion with respect to the jet cross section is beyond the aim of the present work, we investigate the phenomenon by computing the average distribution of the jet radius along the curvilinear coordinate s, where s ∈ [0, 1] is introduced to parametrize the jet path; s = 0 identifies the nozzle, and s = 1 the filament at the collector. In Figure 8 we report for all the three cases the median of the radius conditional distributions computed along the curvilinear coordinate s (the condition is the given value of s). We also report the amplitudes of the conditional distributions evaluated as interquartile range. Here, we observe that all the radius fluctuations are generated close to the nozzle. In particular, at s = 0.05 we already note nonsymmetric fluctuations of the jet radius for cases II and III. Further, we observe larger average values of the curvature k when the counterflow is activated. For instance, the averaged curvature measured at s = 0.05 is 1.1, 1.6, and 1.9 for cases I, II and III, respectively. This is likely due to lift perturbation forces acting in junction with the Coulomb repulsive forces, which produce sharp bends along the jet path already close to the nozzle, providing large fluctuations in the jet cross section. Thus, the quality of the produced fibers is less controllable in the presence of large counterflows (as already evidenced in Figure 6 for case III), and the beneficial effects of the gas stream in decreasing the fiber radius are largely counteracted. Therefore, with the aim of producing thinner fibers and achieving narrower size distributions of the deposited polymer filaments, the counterflow velocity vflow should be carefully tuned, to provide an optimal balance between dissipative and perturbation forces as related to the gas stream.

Figure 7.

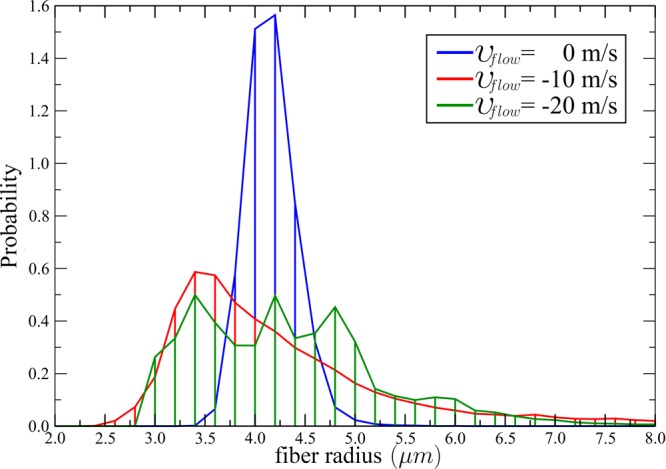
Figure 7

Open in a new tab

Normalized probability of depositing a fiber with a given radius.

Figure 8.

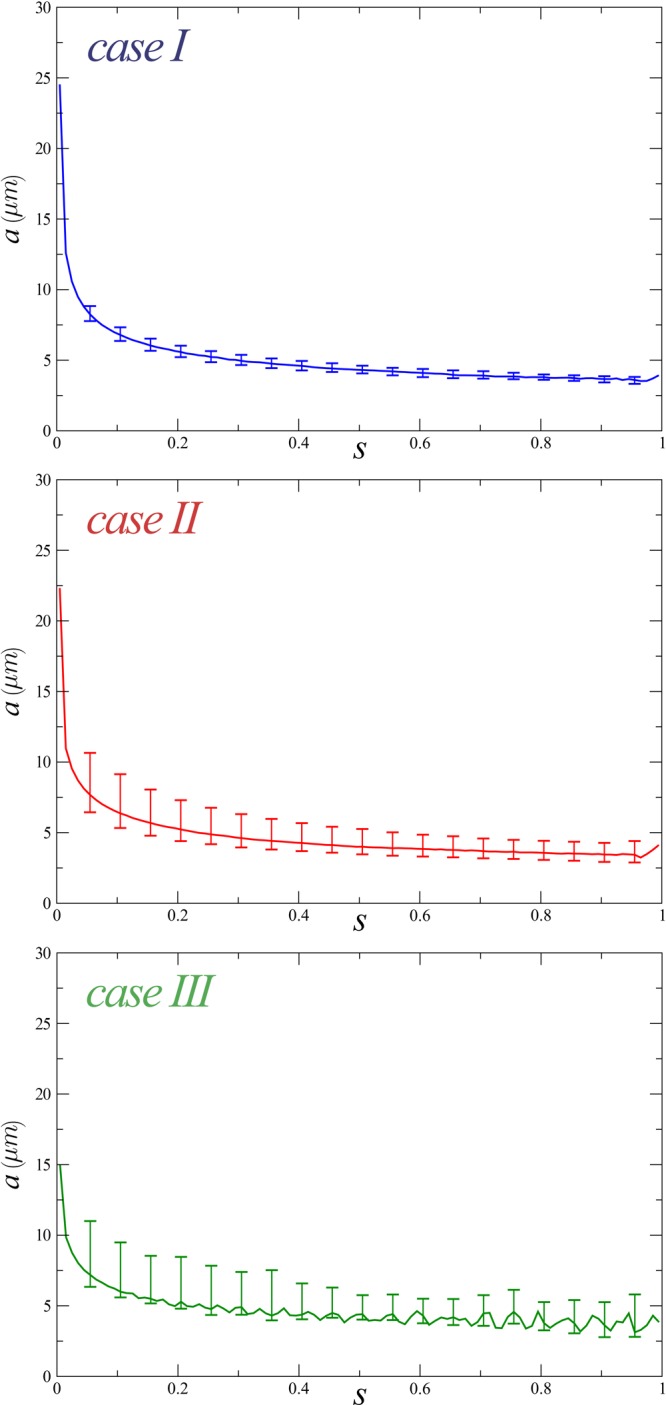
Figure 8

Open in a new tab

Meadian values of the jet radius distributions, a (micrometer), computed along the curvilinear coordinate s for all the three cases. The error bars provide the amplitudes of the distributions evaluated as interquartile range.

4. Summary and Conclusions

Summarizing, we have investigated the dynamics of electrified polymer jets under different conditions of air drag force. In particular, we have probed the effects of a gas flow oriented toward the nozzle on the viscoelastic jet (counterflow) during the electrospinning process, analyzing both the early and the late dynamics. Several observables have been employed to analyze the air drag effects on the jet bending instabilities, showing that the instability cone is altered in its shape and aperture by the presence of a gas stream. Further, the results in terms of fiber deposition were also investigated by a statistical analysis of the late dynamics. We have observed that a controlled gas counterflow might lead to a decrease of the mean value of the fiber cross sectional radius. In particular, our data show a nontrivial trend of the fiber radius as a function of the air flow velocity applied in electrospinning experiment. In fact, the gas flow generates both dissipative and perturbation forces, which provide opposite effects on the resulting fiber cross section. Thinner fibers are obtained by using a gas flow speed of −10 m/s. The complex interplay of effects due to air drag forces deserves a deeper investigation, which will be the subject of future work. However, further investigations will be needed and new terms have to be introduced to describe properly the disordered fiber structure experimentally observed on the collector. In particular, the effect of more complicated modeled perturbations of the nozzle in the presence of air counterflow could provide a more realistic pattern of the filament on the collector. Anyway, the released model represents an important novelty and it might be used for designing a new generation of devices with novel experimental components for gas-assisted electrospinning, to further investigate experimentally this process and to ultimately produce polymeric filaments with finely controlled average diameters and size distribution.

Acknowledgments

The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 306357 (“NANO-JETS”). The authors are grateful to Dr. G. Pontrelli for several useful discussions.

The authors declare no competing financial interest.

References

  1. Reneker D. H.; Chun I. Nanometre Diameter Fibres of Polymer, Produced by Electrospinning. Nanotechnology 1996, 7, 216–223. 10.1088/0957-4484/7/3/009. [DOI] [Google Scholar]
  2. Li D.; Xia Y. Electrospinning of Nanofibers: Reinventing the Wheel?. Adv. Mater. 2004, 16, 1151–1170. 10.1002/adma.200400719. [DOI] [Google Scholar]
  3. Ramakrishna S.; Fujihara K.; Teo W.-E.; Lim T.-C.; Ma Z.. An Introduction to Electrospinning and Nanofibers; World Scientific: Hackensack, NJ, USA, 2005; Vol. 90. [Google Scholar]
  4. Luo C.; Stoyanov S. D.; Stride E.; Pelan E.; Edirisinghe M. Electrospinning versus Fibre Production Methods: from Specifics to Technological Convergence. Chem. Soc. Rev. 2012, 41, 4708–4735. 10.1039/c2cs35083a. [DOI] [PubMed] [Google Scholar]
  5. Wendorff J. H.; Agarwal S.; Greiner A.. Electrospinning: Materials, Processing, and Applications; John Wiley & Sons: West Sussex, U.K., 2012. [Google Scholar]
  6. Pisignano D.Polymer Nanofibers: Building Blocks for Nanotechnology; Royal Society of Chemistry: London, U.K., 2013. [Google Scholar]
  7. Persano L.; Camposeo A.; Pisignano D. Active Polymer Nanofibers for Photonics, Electronics, Energy Generation and Micromechanics. Prog. Polym. Sci. 2015, 43, 48–95. 10.1016/j.progpolymsci.2014.10.001. [DOI] [Google Scholar]
  8. Rayleigh L. On the Equilibrium of Liquid Conducting Masses Charged with Electricity. Philos. Mag. Series 5 1882, 14, 184–186. 10.1080/14786448208628425. [DOI] [Google Scholar]
  9. Zeleny J. Instability of Electrified Liquid Surfaces. Phys. Rev. 1917, 10, 1–6. 10.1103/PhysRev.10.1. [DOI] [Google Scholar]
  10. Jeans J. H.The Mathematical Theory of Electricity and Magnetism; Cambridge University Press: Cambridge, UK., 1908. [Google Scholar]
  11. Fong H.; Chun I.; Reneker D. Beaded Nanofibers Formed During Electrospinning. Polymer 1999, 40, 4585–4592. 10.1016/S0032-3861(99)00068-3. [DOI] [Google Scholar]
  12. Theron S.; Zussman E.; Yarin A. Experimental Investigation of the Governing Parameters in the Electrospinning of Polymer Solutions. Polymer 2004, 45, 2017–2030. 10.1016/j.polymer.2004.01.024. [DOI] [Google Scholar]
  13. Carroll C. P.; Joo Y. L. Electrospinning of Viscoelastic Boger Fluids: Modeling and Experiments. Phys. Fluids 2006, 18, 053102. 10.1063/1.2200152. [DOI] [Google Scholar]
  14. Montinaro M.; Fasano V.; Moffa M.; Camposeo A.; Persano L.; Lauricella M.; Succi S.; Pisignano D. Sub-ms Dynamics of the Instability Onset of Electrospinning. Soft Matter 2015, 11, 3424–3431. 10.1039/C4SM02708F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wang X.; Um I. C.; Fang D.; Okamoto A.; Hsiao B. S.; Chu B. Formation of Water-Resistant Hyaluronic Acid Nanofibers by Blowing-Assisted Electro-Spinning and Non-Toxic Post Treatments. Polymer 2005, 46, 4853–4867. 10.1016/j.polymer.2005.03.058. [DOI] [Google Scholar]
  16. Yao Y.; Zhu P.; Ye H.; Niu A.; Gao X.; Wu D. Polysulfone Nanofibers Prepared by Electrospinning and Gas/Jet-Electrospinning. Front. Chem. Chin. 2006, 1, 334–339. 10.1007/s11458-006-0041-4. [DOI] [Google Scholar]
  17. Kim G. H.; Yoon H. A Direct-Electrospinning Process by Combined Electric Field and Air-Blowing System for Nanofibrous Wound-Dressings. Appl. Phys. A: Mater. Sci. Process. 2008, 90, 389–394. 10.1007/s00339-007-4330-0. [DOI] [Google Scholar]
  18. Lin Y.; Yao Y.; Yang X.; Wei N.; Li X.; Gong P.; Li R.; Wu D. Preparation of Poly (Ether Sulfone) Nanofibers by Gas-Jet/Electrospinning. J. Appl. Polym. Sci. 2008, 107, 909–917. 10.1002/app.26445. [DOI] [Google Scholar]
  19. Zhmayev E.; Cho D.; Joo Y. L. Nanofibers From Gas-Assisted Polymer Melt Electrospinning. Polymer 2010, 51, 4140–4144. 10.1016/j.polymer.2010.06.058. [DOI] [Google Scholar]
  20. Hsiao H.-Y.; Huang C.-M.; Liu Y.-Y.; Kuo Y.-C.; Chen H. Effect of Air Blowing on the Morphology and Nanofiber Properties of Blowing-Assisted Electrospun Polycarbonates. J. Appl. Polym. Sci. 2012, 124, 4904–4914. 10.1002/app.35599. [DOI] [Google Scholar]
  21. Reneker D. H.; Yarin A. L.; Fong H.; Koombhongse S. Bending Instability of Electrically Charged Liquid Jets of Polymer Solutions in Electrospinning. J. Appl. Phys. 2000, 87, 4531–4547. 10.1063/1.373532. [DOI] [Google Scholar]
  22. Yarin A. L.; Koombhongse S.; Reneker D. H. Taylor Cone and Jetting from Liquid Droplets in Electrospinning of Nanofibers. J. Appl. Phys. 2001, 90, 4836–4846. 10.1063/1.1408260. [DOI] [Google Scholar]
  23. Hohman M. M.; Shin M.; Rutledge G.; Brenner M. P. Electrospinning and Electrically Forced Jets. I. Stability Theory. Phys. Fluids 2001, 13, 2201–2220. 10.1063/1.1383791. [DOI] [Google Scholar]
  24. Fridrikh S. V.; Jian H. Y.; Brenner M. P.; Rutledge G. C. Controlling the Fiber Diameter During Electrospinning. Phys. Rev. Lett. 2003, 90, 144502. 10.1103/PhysRevLett.90.144502. [DOI] [PubMed] [Google Scholar]
  25. Spivak A.; Dzenis Y.; Reneker D. A model of Steady State Jet in the Electrospinning Process. Mech. Res. Commun. 2000, 27, 37–42. 10.1016/S0093-6413(00)00060-4. [DOI] [Google Scholar]
  26. Feng J. The Stretching of an Electrified Non-Newtonian Jet: A Model for Electrospinning. Phys. Fluids 2002, 14, 3912–3926. 10.1063/1.1510664. [DOI] [Google Scholar]
  27. Feng J. Stretching of a Straight Electrically Charged Viscoelastic Jet. J. Non-Newtonian Fluid Mech. 2003, 116, 55–70. 10.1016/S0377-0257(03)00173-3. [DOI] [Google Scholar]
  28. Hohman M. M.; Shin M.; Rutledge G.; Brenner M. P. Electrospinning and Electrically Forced Jets. II. Applications. Phys. Fluids 2001, 13, 2221–2236. 10.1063/1.1384013. [DOI] [Google Scholar]
  29. Lauricella M.; Pontrelli G.; Pisignano D.; Succi S. Nonlinear Langevin Model for the Early-Stage Dynamics of Electrospinning Jets. Mol. Phys. 2015, 113, 2435–2441. 10.1080/00268976.2015.1031957. [DOI] [Google Scholar]
  30. Ziabicki A.; Kawai H.. High-Speed Fiber Spinning: Science and Engineering Aspects; Krieger Publishing Co: Malabar, FL, USA, 1991. [Google Scholar]
  31. Lauricella M.; Pontrelli G.; Coluzza I.; Pisignano D.; Succi S. JETSPIN: a Specific-Purpose Open-Source Software for Simulations of Nanofiber Electrospinning. Comput. Phys. Commun. 2015, 197, 227–238. 10.1016/j.cpc.2015.08.013. [DOI] [Google Scholar]
  32. JETSPIN is freeware, and it can be downloaded via http://www.nanojets.eu/downloads.html.
  33. Sinha-Ray S.; Yarin A. L.; Pourdeyhimi B. Meltblowing: I-Basic Physical Mechanisms and Threadline Model. J. Appl. Phys. 2010, 108, 034912. 10.1063/1.3457891. [DOI] [Google Scholar]
  34. Yarin A. L.; Pourdeyhimi B.; Ramakrishna S.. Fundamentals and Applications of Micro and Nanofibers; Cambridge University Press: Cambridge, U.K., 2014. [Google Scholar]
  35. Yarin A. L.Free Liquid Jets and Films: Hydrodynamics and Rheology; Longman Scientific & Technical Harlow: Essex, U.K., 1993. [Google Scholar]
  36. Durrett R.Probability: Theory and Examples; Cambridge University Press: Cambridge, U.K., 2010. [Google Scholar]
  37. Coluzza I.; Pisignano D.; Gentili D.; Pontrelli G.; Succi S. Ultrathin Fibers from Electrospinning Experiments under Driven Fast-Oscillating Perturbations. Phys. Rev. Appl. 2014, 2, 054011. 10.1103/PhysRevApplied.2.054011. [DOI] [Google Scholar]
  38. Lauricella M.; Pontrelli G.; Coluzza I.; Pisignano D.; Succi S. Different Regimes of the Uniaxial Elongation of Electrically Charged Viscoelastic Jets due to Dissipative Air Drag. Mech. Res. Commun. 2015, 69, 97–102. 10.1016/j.mechrescom.2015.06.014. [DOI] [Google Scholar]
  39. Platen E.Stochastic Differential Systems; Springer: London, UK., 1987; pp 187–193. [Google Scholar]
  40. Kloeden P. E.; Platen E.. Numerical Solution of Stochastic Differential Equations; Springer: London, U.K., 1992. [Google Scholar]
  41. Benzi R.; Tripiccione R.; Massaioli F.; Succi S.; Ciliberto S. On the Scaling of the Velocity and Temperature Structure Functions in Rayleigh-Bénard Convection. EPL (Europhys. Lett.) 1994, 25, 341. 10.1209/0295-5075/25/5/005. [DOI] [Google Scholar]
  42. Ottaviani M.; Romanelli F.; Benzi R.; Briscolini M.; Santangelo P.; Succi S. Numerical simulations of ion temperature gradient-driven turbulence. Phys. Fluids B 1990, 2 (1), 67–74. 10.1063/1.859540. [DOI] [Google Scholar]

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES