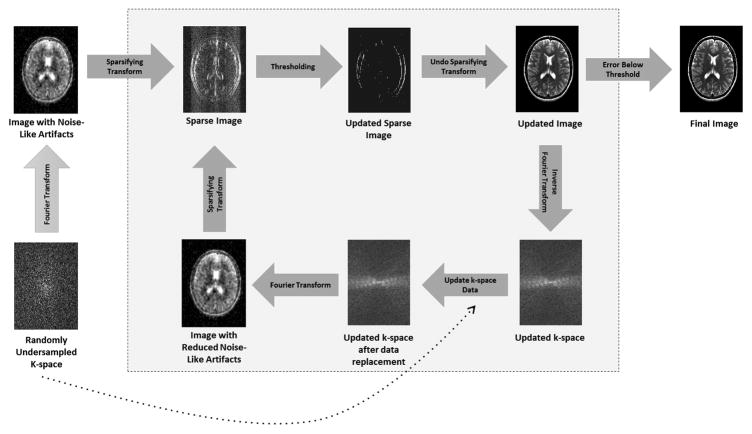
Figure 7.

A schematic of a simplified compressed sensing reconstruction. Randomly undersampled k-space data are collected (bottom left), leading to an image which exhibits noise-like aliasing artifacts (top left). A sparse representation of this undersampled image can be obtained by applying a sparsifying transform such as finite differences, which highlights edges. Because the artifacts look like noise, it is possible to retain most of the significant pixels in the sparse image while removing some noise-like artifacts by thresholding this image. After thresholding, only true edges remain, although some may have been lost in the thresholding process. An updated image is generated by “undoing” the sparsifying transform, and this updated image with reduced aliasing artifacts is converted back to k-space. This k-space may contain data that is different from the collected k-space data after the thresholding step. Therefore, to ensure data consistency, the original k-space data are reinserted into the k-space of the updated image. This updated k-space is then converted into an image, which is now both consistent with the original data and contains reduced aliasing artifacts, and the loop begins again. When the error between the previous iteration of the updated image and the current iteration reaches the stopping criteria set by the user, the iteration loop is broken and the final image is output.