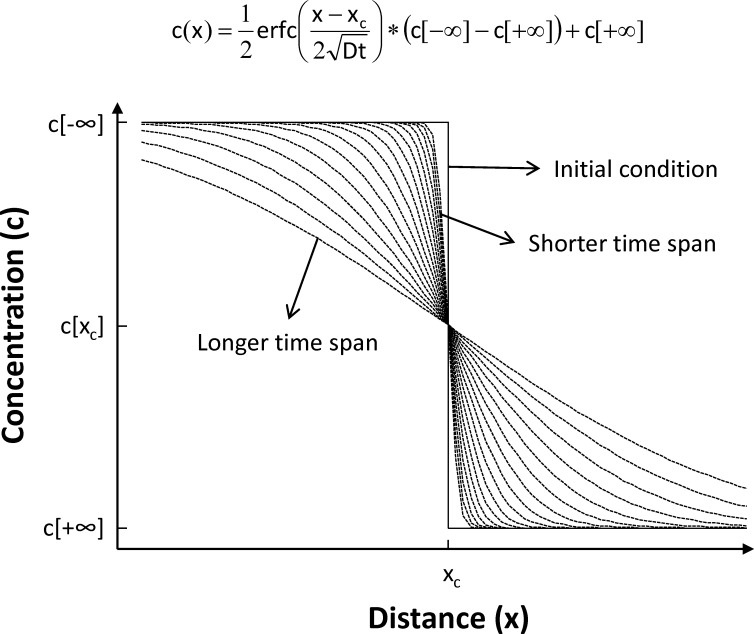
Fig 1. Principle behind diffusion chronometry.

We use a 1D model to calculate the time since the inception of a given compositional contact in a crystal. We assume an initially infinitely sharp “step function” boundary (indicated as “Initial condition” in the diagram), which becomes progressively less sharp with time (shown as a series of curves). This problem has a well-known solution, with the resulting damped curve being described by a complementary error function (erfc) as shown in the figure. We use a least-squares procedure to find the best-fit erfc function, from which we can extract the value of ($2\sqrt{Dt}$); using experimentally determined values of the diffusion coefficient D, we can then calculate the residence time of a given contact and the growth time for the crystal region rimward from the contact. We can also measure the growth distance from our images, from which we calculate average crystal rim growth rates.