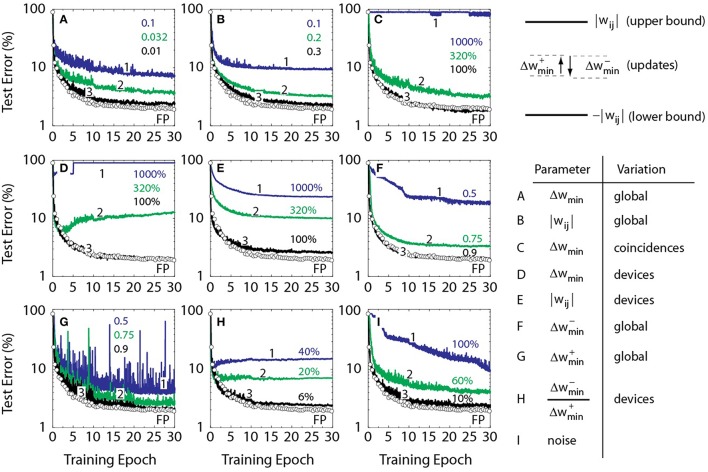
Figure 3.

Test error of DNN with the MNIST dataset. Open white circles correspond to a baseline model where the training is performed using the conventional update rule of Equation (1). All solid lines assume a stochastic model with BL = 10 and k = 0. (A) Lines 1, 2, and 3 correspond to a stochastic model with Δw_min = 0.1, 0.032, and 0.01, respectively. All curves in (B–I) use Δw_min = 0.001. (B) Lines 1, 2, and 3 correspond to a stochastic model with weights bounded to 0.1, 0.2, and 0.3, respectively. (C) Lines 1, 2, and 3 correspond to a stochastic model with a coincidence-to-coincidence variation in Δw_min of 1000, 320, and 100%, respectively. (D) Lines 1, 2, and 3 correspond to a stochastic model with device-to-device variation in Δw_min of 1000, 320 and 100%, respectively. (E) Lines 1, 2, and 3 correspond to a stochastic model with device-to-device variation in the upper and lower bounds of 1000, 320 and 100%, respectively. All solid lines in E have a mean value of 1.0 for upper bound (and −1.0 for lower bound). (F) Lines 1, 2, and 3 correspond to a stochastic model, where down changes are weaker by 0.5, 0.75, and 0.9, respectively. (G) Lines 1, 2, and 3 correspond to a stochastic model, where up changes are weaker by 0.5, 0.75, and 0.9, respectively. (H) Lines 1, 2, and 3 correspond to a stochastic model with device-to-device variation in the up and down changes by 40, 20 and 6%, respectively. (I) Lines 1, 2, and 3 correspond to a stochastic model with a noise in vector-matrix multiplication of 100, 60, and 10%, respectively, normalized on activation function temperature which is unity.