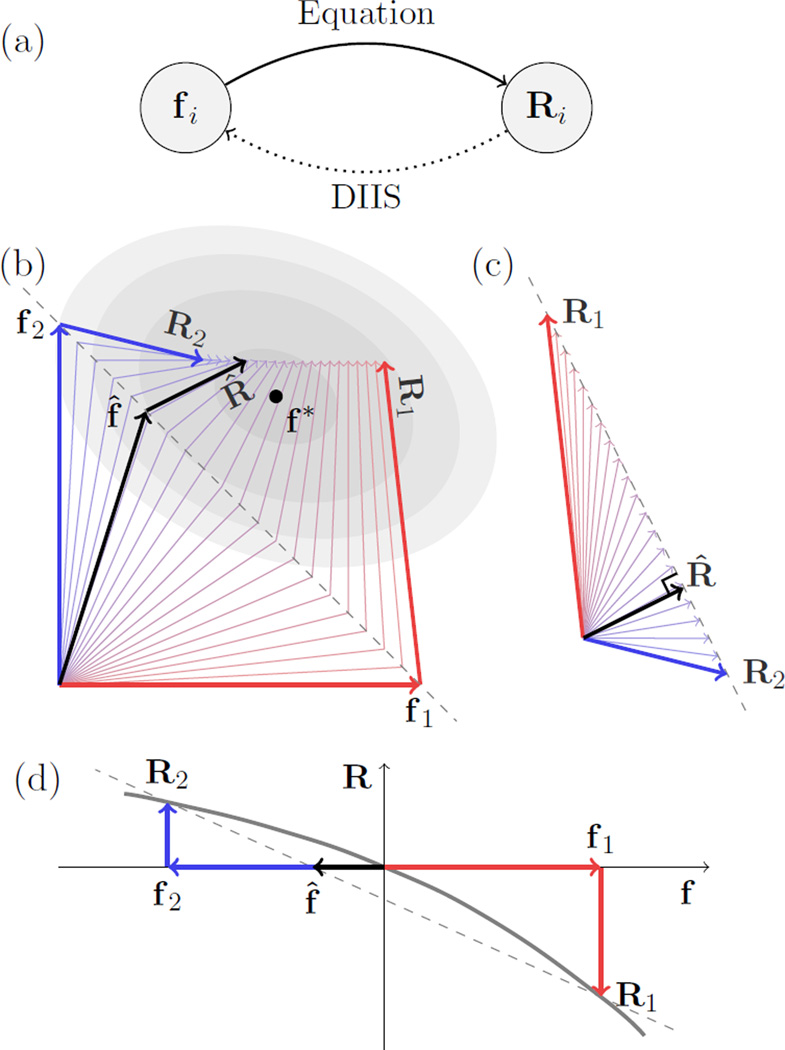
Figure 1.

Schematic illustrations of the method of direct inversion of the iterative subspace (DIIS). (a) As an iterative method, DIIS solves the equation, R(f) = 0, by a feedback loop. When the equation is applied to a trial solution, represented by vector f_i, we get a residual vector R_i ≡ R(f_i), whose magnitude indicates the error. Ideally, if f_i were the true solution, R_i would be zero. In the feedback step, we correct f_i using R_i. The task of DIIS is to construct from a few previous vectors accumulated during the iteration an optimal trial vector f̂ with hopefully the smallest error ‖R̂‖ to help the next round of iteration. (b) and (c) Given a basis of M (two here) trial vectors, DIIS seeks the combination $\hat{\mathbf{R}}={\sum }_{i=1}^M{c}_i{\mathbf{R}}_i$ that minimises the magnitude ‖R̂‖ under the constraint ${\sum }_{i=1}^M{c}_i=1$ [panel (c)]. The corresponding combination of the trial vectors, $\hat{\mathbf{f}}={\sum }_{i=1}^M{c}_i{\mathbf{f}}_i$, is expected to be close to true solution, f*. Then, we construct the new trial vector as f⁽ⁿ⁾ = f̂ + R̂ and use it to update the basis for the next round of iteration. (d) If the vectors are one-dimensional (i.e., scalars), it is possible to find a vanishing R̂, and DIIS is equivalent to the secant method.