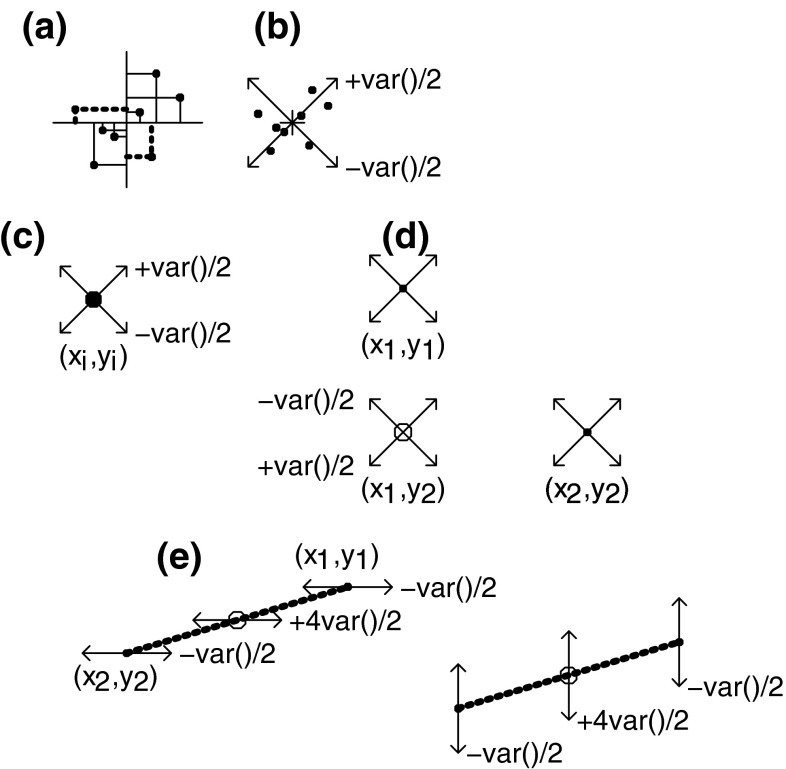
Fig. 12.

The diverse geometries of shape coordinate covariances. a The usual definition: cov(x, y) is the average of the signed areas of the rectangles drawn. (Areas of rectangles drawn in dashed line are taken with a minus sign.) Every rectangle includes the centroid of all the points (x, y) as its fourth corner. b Equivalent characterization as half the difference of two variances, that along the (1, 1) diagonal of the scatter grid and that along the $(-1,1)$ diagonal. Rotating the coordinate system of this diagram by ${90}^{\circ }$ reverses the sign of the covariance. c For the two shape coordinates of a single landmark point the scheme in panel (b) is adequate. d The covariance of any x-coordinate with any y-coordinate reduces to the geometry of a new, fictitious composite landmark, open circle, that combines the chosen x-coordinate with the chosen y. e The covariance of two x-shape coordinates (left) is an entirely different matter that begins with the other covariance identity, the excess of the variance of an average of two quantities (open circle) over half the sum of their variances separately. Rotating the coordinate system of this construction by ${90}^{\circ }$ does not change the sign of anything, but results in an entirely different construction (right), the covariance of the corresponding pair of y-shape coordinates