Significance
Bacterial adaptation through horizontal gene transfer is central to microbial evolution and, in the context of antibiotic resistance, represents a growing clinical threat. Conjugative plasmids are key mediators of genetic exchange both within and between species. Experimental studies have mostly focused on plasmid population dynamics in single-species populations, but between-species transfer could counteract purifying selection and maintain plasmids in hosts that would otherwise lose them. We show that plasmids can be lost from single-species populations, even when their genes are under selection, because beneficial genes are captured by the chromosome. In contrast, experiments and models show that, in a two-species community, between-species transfer maintains community-wide access to plasmids, promoting the spread of the ecologically and clinically important genes they carry.
Keywords: horizontal gene transfer, plasmids, mobile genetic elements, microbial ecology
Abstract
Horizontal gene transfer is a fundamental process in bacterial evolution that can accelerate adaptation via the sharing of genes between lineages. Conjugative plasmids are the principal genetic elements mediating the horizontal transfer of genes, both within and between bacterial species. In some species, plasmids are unstable and likely to be lost through purifying selection, but when alternative hosts are available, interspecific plasmid transfer could counteract this and maintain access to plasmid-borne genes. To investigate the evolutionary importance of alternative hosts to plasmid population dynamics in an ecologically relevant environment, we established simple soil microcosm communities comprising two species of common soil bacteria, Pseudomonas fluorescens and Pseudomonas putida, and a mercury resistance (HgR) plasmid, pQBR57, both with and without positive selection [i.e., addition of Hg(II)]. In single-species populations, plasmid stability varied between species: although pQBR57 survived both with and without positive selection in P. fluorescens, it was lost or replaced by nontransferable HgR captured to the chromosome in P. putida. A simple mathematical model suggests these differences were likely due to pQBR57’s lower intraspecific conjugation rate in P. putida. By contrast, in two-species communities, both models and experiments show that interspecific conjugation from P. fluorescens allowed pQBR57 to persist in P. putida via source–sink transfer dynamics. Moreover, the replacement of pQBR57 by nontransferable chromosomal HgR in P. putida was slowed in coculture. Interspecific transfer allows plasmid survival in host species unable to sustain the plasmid in monoculture, promoting community-wide access to the plasmid-borne accessory gene pool and thus potentiating future evolvability.
Horizontal gene transfer (HGT) is a key process in bacterial evolution, driving the spread of ecologically and clinically important traits such as resistances to environmental toxins and antibiotics (1). Conjugative plasmids are extrachromosomal genetic elements that carry genes for their horizontal transfer between bacteria (i.e., conjugation) and are principal mediators of HGT both within and between species (2, 3). Because plasmid-borne “accessory genes” (i.e., genes not directly involved in core plasmid functions) can enhance the virulence, metabolism, or resistance of bacterial hosts (1), the population dynamics of plasmids is fundamentally important to understanding bacterial adaptation (3).
Plasmids impose costs on their hosts (4), and theory suggests that, without positive selection for accessory genes, plasmids should be lost from bacterial populations due to purifying selection unless counteracted by a high rate of conjugation (5, 6). Under positive selection, plasmids should also eventually be lost as selection favors chromosomal integration of accessory genes and loss of the redundant plasmid (5). In addition to the immediate loss of accessory genes, the loss of conjugative plasmids from populations decreases the potential for HGT, thereby diminishing a key mode for acquisition of novel adaptive genes and thus limiting bacterial evolvability.
Several mechanisms could act to maintain plasmids. Compensatory evolution can ameliorate plasmid cost, thereby weakening selection against the plasmid (7–9). However, this process is unlikely to stabilize highly unstable plasmids or maintain plasmids in small populations where the rate of plasmid loss is likely to exceed the rate of compensatory evolution. Plasmids may carry genes that directly enhance their stability, such as partitioning genes or toxin–antitoxin systems, but even when present such systems are imperfect, resulting in plasmid-free segregants (10). Plasmids can also be maintained within a host species as infectious elements, provided conjugation rates are high (e.g., ref. 11).
An alternative mechanism is for plasmid loss in a focal host species to be counteracted by ongoing transfer from another species in which the plasmid is stably maintained. Such interspecific conjugation, analogous to transmission of infectious disease from a reservoir host (12), could maintain access to the mobile gene pool, allowing the focal species to remain evolutionarily responsive to temporally or spatially variable selection (3). Plasmids can be shared by a considerable fraction of the microbial community (13), but surprisingly there have been few experimental tests of how the presence of alternative hosts affects plasmid population dynamics, particularly over periods longer than a few days. Moreover, most studies of plasmid dynamics have been performed in well-mixed rich laboratory media, which do not adequately represent the physical structure or nutrient availability in most natural microbial communities (14, 15). Structured communities may present fewer opportunities for plasmid donors to encounter recipients, but clustering of genotypes in space may promote species coexistence (16) and also allow plasmids to rapidly sweep through naïve recipient populations once encountered (17, 18).
To test how the presence of alternative host species affects plasmid population dynamics, we established populations of Pseudomonas fluorescens SBW25 and Pseudomonas putida KT2440 either individually (“single species”), or together (“coculture”), in sterile soil microcosms, which offer a spatially structured, low-resource, and near-natural environment (19). Pseudomonads such as P. fluorescens and P. putida are widespread and often coexist in natural soil communities (20). Populations were founded with a mercury resistance (HgR) plasmid [the 307-kb pQBR57, isolated from the same site as P. fluorescens SBW25 (21)] at ∼50% starting frequency, with approximately equal numbers of pQBR57-bearers (pQBR57+) in each species for the coculture treatment. Every 4 d, samples were transferred into fresh microcosms that had either been pretreated with selective levels of mercuric chloride [16 µg/g Hg(II)] or with an equal volume of water [0 µg/g Hg(II)]. Such transfers represent a simple controllable regime that acts as a proxy for the dynamic “turnover” of nutrients occurring in soil habitats (22), and 16 µg/g Hg(II) corresponds to specific mercury contamination, such as in industrial or postindustrial sites (23). The dynamics of the bacterial populations, the frequency of pQBR57, and the frequency of the mercury reductase gene (merA) were tracked over 65 transfers (approximately ∼440 generations; Supporting Information).
Results
Plasmid Dynamics Were Strongly Affected by Host Species and Culture Conditions.
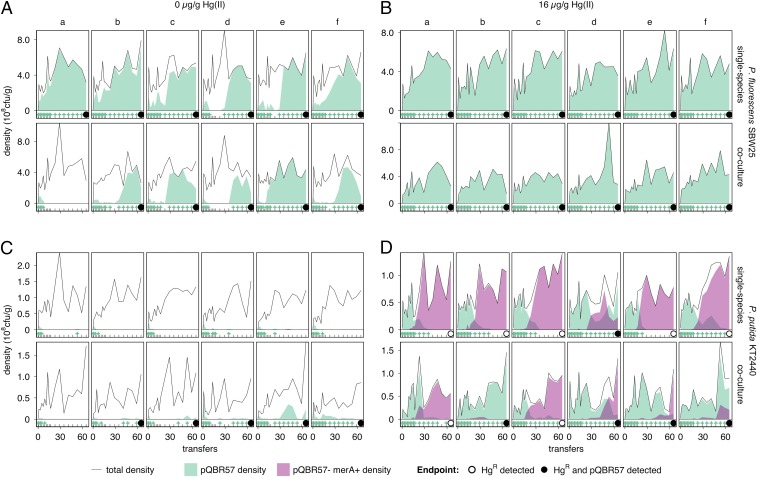
The dynamics of pQBR57 varied greatly between species and with Hg(II) treatment. pQBR57 was generally maintained in P. fluorescens under both Hg(II) treatments, going extinct in only one replicate [replicate a, 0 µg/g Hg(II), coculture]. Under 0 µg/g Hg(II) (Fig. 1A), plasmid frequencies were variable between replicates and across time, particularly during the early part of the experiment. No significant effect of living alongside P. putida could be detected in terms of pQBR57 survival (Fisher’s exact test, P = 1), constancy (Wilcoxon signed-rank test, Z = 0, P = 1), or dynamics [generalized linear mixed-effects model (GLMM), effect of coculture, parametric bootstrapping P = 0.08]. Under 16 µg/g Hg(II), both in one-species and coculture treatments (Fig. 1B), pQBR57 fixed in P. fluorescens by transfer 5 and remained so until the end of the experiment. P. fluorescens was therefore a favorable host for pQBR57, in that it generally maintained the plasmid regardless of selective environment.
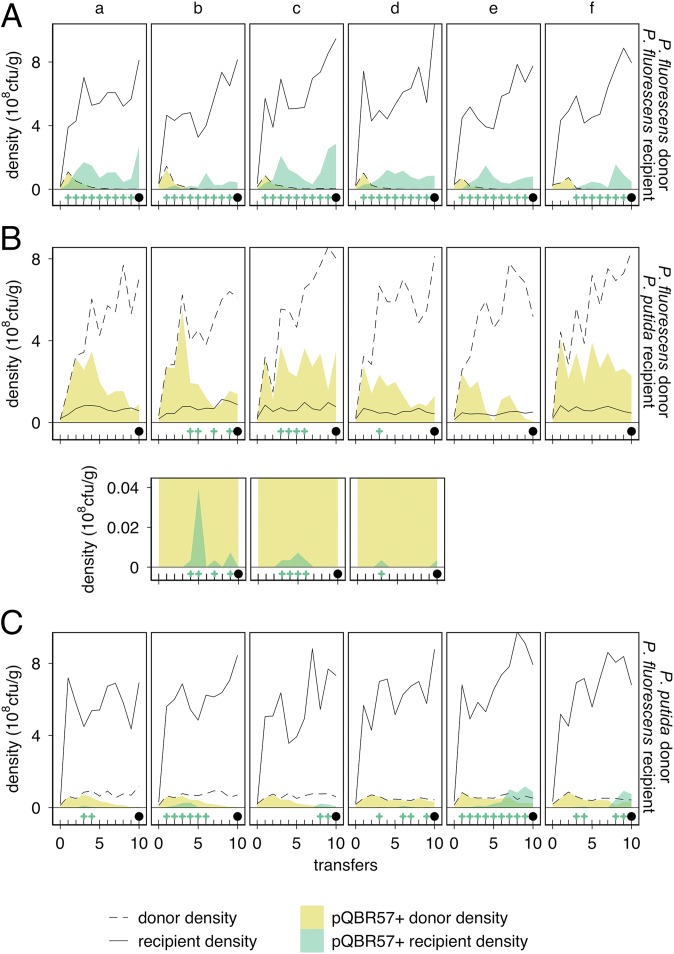
Fig. 1.
Coculture with favorable host P. fluorescens promotes plasmid carriage in unfavorable P. putida. (A) P. fluorescens populations evolved with 0 µg/g Hg(II). The upper row of subpanels shows single-species populations; the lower row shows populations cultured alongside P. putida (coculture). Six replicate populations (columns, labeled a–f) were initiated for each treatment. Each subpanel shows, for an individual population, total density at transfer (solid line), the density of pQBR57+ (filled green area below the line), and the density of pQBR57– merA+ mutants (filled purple area below the line). For clarity, tick marks at the bottom of each subpanel indicate sampling times, and green “+” symbols indicate detection of pQBR57. A black circle at the final sampling point (transfer 65) indicates that HgR remained in the population at the end of the experiment; filled circles indicate pQBR57 (and HgR) remained. Note that no pQBR57– merA+ mutants were detected in P. fluorescens. (B) P. fluorescens populations evolved with 16 µg/g Hg(II). As in A, except evolved with 16 µg/g Hg(II). (C) P. putida populations evolved with 0 µg/g Hg(II). As in A, except populations were P. putida. The lower row of subpanels shows populations cultured alongside P. fluorescens (coculture). Each population of cocultured P. putida a–f was grown with the corresponding cocultured P. fluorescens population (a–f, A). (D) P. putida populations evolved with 16 µg/g Hg(II). As in C, except evolved with 16 µg/g Hg(II). Different y-axis scales are used for each species: P. fluorescens density was ∼5x P. putida.
In contrast, pQBR57 was poorly maintained in single-species P. putida populations. In the 0 µg/g Hg(II) single-species treatment (Fig. 1C, upper row), pQBR57 decreased rapidly in frequency and ultimately went extinct in all replicates, resulting in a completely Hg(II)-sensitive population. In the 16 µg/g Hg(II) single-species treatment (Fig. 1D, upper row), pQBR57 frequency increased to near fixation in all populations before transfer 5. However, mutants that lost pQBR57 but retained the mercury reductase merA gene (pQBR57– merA+) soon emerged and reached high frequency (>50%) in all populations. In five of six replicates, pQBR57– merA+ mutants eventually outcompeted plasmid bearers, resulting in plasmid extinction by the end of the experiment. In single-species populations, therefore, pQBR57 was significantly more likely to go extinct when its host was P. putida rather than P. fluorescens, both under parasitic 0 µg/g Hg(II) (Fisher’s exact test, P = 0.0022) and mutualistic 16 µg/g Hg(II) (P = 0.015) conditions. P. putida was therefore an unfavorable pQBR57 host, in that it generally lost the plasmid regardless of selective environment.
However, living in coculture with P. fluorescens had a positive effect on pQBR57 carriage by P. putida under both Hg(II) conditions. In 0 µg/g Hg(II) (Fig. 1C, lower row), five of six cocultured P. putida populations carried pQBR57 at detectable levels during the experiment, particularly in two replicates (e and f). Control experiments, in which we mixed plasmid-containing P. fluorescens and plasmid-free P. putida immediately before spreading on selective media, did not yield any transconjugants (Supporting Information), suggesting that these clones carried pQBR57 in situ rather than acquiring it on the surface of the agar plate. pQBR57 therefore benefitted from a reduced chance of extinction in cocultured P. putida in 0 µg/g Hg(II) (Fisher’s exact test, P = 0.015), and we detected a positive effect of coculture on the frequency of P. putida plasmid carriers over time (GLMM, effect of coculture:transfer, parametric bootstrapping P = 0.025; effect of coculture P = 0.006). The exception was replicate a, in which pQBR57 also went extinct in the cocultured P. fluorescens population.
In 16 µg/g Hg(II) (Fig. 1D, lower row), like with single-species culture, pQBR57– merA+ mutants arose in all cocultured P. putida populations. However, in two of six cocultured populations these mutants remained ≤30%, and in one replicate (b) they were subsequently lost. Overall, the presence of P. fluorescens had a positive effect on the frequency of plasmid carriage in P. putida in 16 µg/g Hg(II) (GLMM, effect of coculture:transfer, parametric bootstrapping P = 0.045; effect of coculture P = 0.008), although we did not detect a significant difference in plasmid extinction between single-species and cocultured P. putida (Fisher’s exact test, P = 0.24), probably because strong selection for HgR, and hence pQBR57 initially, resulted in high frequencies of pQBR57+ P. putida in all populations in the early part of the experiment. Coculturing with the favorable host P. fluorescens therefore enhanced plasmid presence in the unfavorable host P. putida, both when plasmid-borne genes were under positive selection [16 µg/g Hg(II)] and when the plasmid was parasitic [0 µg/g Hg(II)].
pQBR57 Was Sustained by Conjugative Transfer.
Within species, theory predicts that variation in plasmid dynamics is determined by the net cost of carriage and the rates of conjugative transfer and segregational loss (5, 6). Differences in pQBR57 stability between P. putida and P. fluorescens cannot be explained by costs, because we found pQBR57 to be more costly in P. fluorescens, which maintained the plasmid, than in P. putida, which did not (Supporting Information). In contrast, we found that pQBR57 had a relatively high intraspecific conjugation rate in P. fluorescens, ∼1,000× that in P. putida (Supporting Information), which might explain maintenance and spread of pQBR57 in P. fluorescens without positive selection. Furthermore, we could detect interspecific transfer of pQBR57 in both directions (Supporting Information). If pQBR57 could be maintained in P. fluorescens by intraspecific conjugation, then in coculture P. fluorescens might act as a source for P. putida through interspecific conjugation. Alternatively, variation in the rate at which plasmid-free segregants arise (segregation rate) may explain differences in plasmid maintenance between the species.
To explore the role of these processes, we first tested the effect of conjugation in a simple mass action model of plasmid dynamics (24) adapted to include two species. For species 1, the change in the number of plasmid-free bacteria over time is given by the following:
| [1] |
and the change in the number of plasmid-containing-bacteria is given by the following:
| [2] |
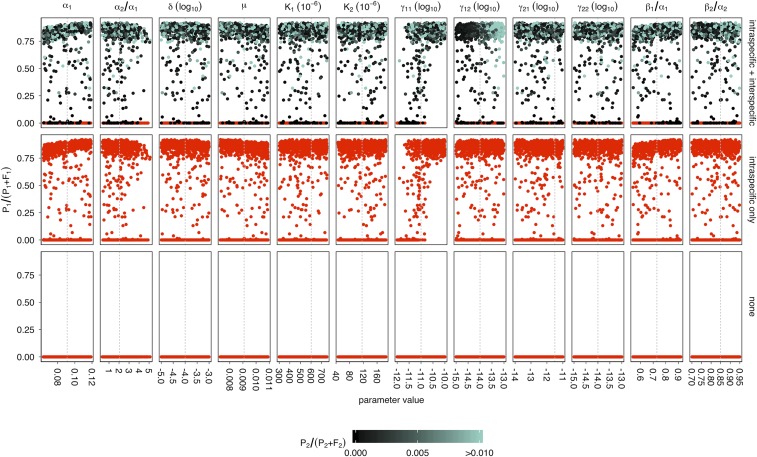
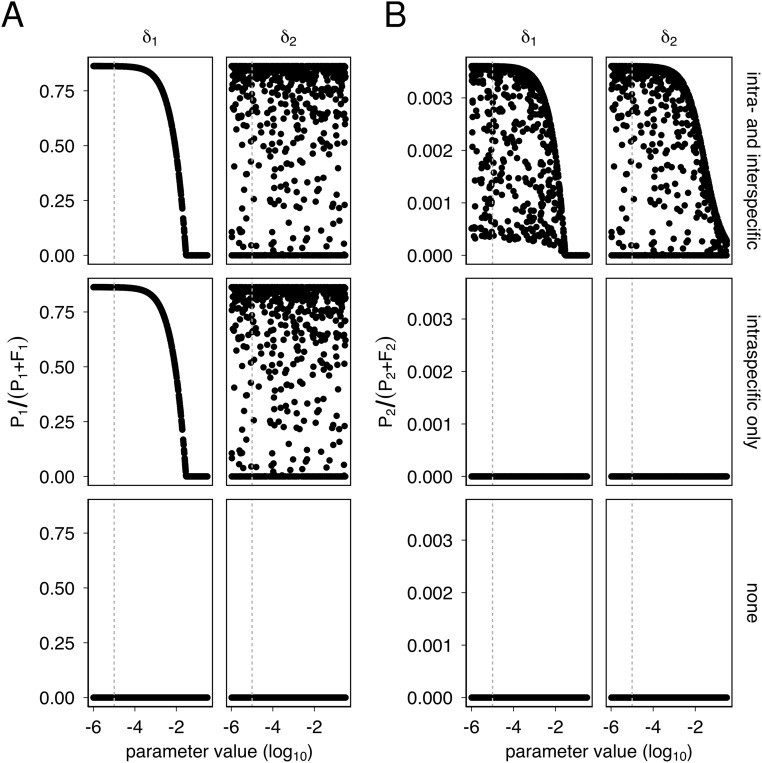
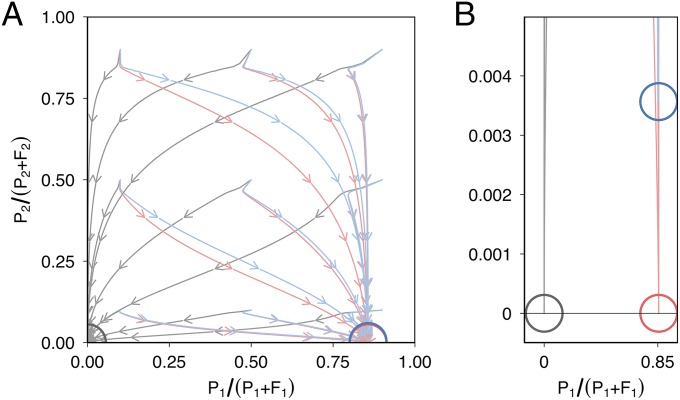
where is the species 1-specific plasmid-free growth rate, is the species 1-specific plasmid-bearing growth rate, is the species 1 intraspecific conjugation rate, is the interspecific conjugation rate from species 2 to species 1, is the species 1-specific carrying capacity, is the plasmid segregation rate, and is the washout rate. Similar equations were written using the species 2-specific parameters to describe the dynamics of and , with intraspecific conjugation rate and interspecific conjugation rate from species 1 to species 2, . Because we did not detect a significant effect of coculture on the growth rates or carrying capacities of P. fluorescens or P. putida (Supporting Information), we assumed that interspecific competition did not greatly affect growth dynamics. Parameter estimates were obtained experimentally for P. fluorescens (“species 1”) and P. putida (“species 2”; Supporting Information and Table S1) where possible, and the four-equation model run with varying starting plasmid frequencies for 5,000 iterations either with interspecific and intraspecific conjugation, with intraspecific conjugation only, or without any conjugation. To test the robustness of the qualitative model predictions, we also ran the model with sets of parameters randomly drawn from a wide range of plausible values (Figs. S1–S3). The model with no conjugation ultimately saw plasmid extinction in both species (Fig. 2). With intraspecific conjugation, the plasmid stabilized at ∼85% in species 1, although it went extinct in species 2. Importantly, adding interspecific conjugation allowed plasmid persistence in both species, albeit at low frequency in species 2 (∼0.35%; Fig. 2B). Further exploration of the parameter space showed that plasmid survival in species 1 was due to higher levels of intraspecific conjugation, which in turn was due to conjugation rate and to a lesser extent the larger population size of species 1 (Fig. S1), whereas plasmid survival in species 2 depended on plasmid survival in species 1 and interspecific conjugation from species 1 to species 2 (Fig. S2). Segregation rates, however, could be varied over a large range without qualitative effect on the model predictions, suggesting the observed plasmid dynamics are better explained by intraspecific and interspecific conjugation (Fig. S3).
Table S1.
Parameter values and SEs used in the mass action model
| Name | Variable measured | Estimate | Source |
| Species 1 growth rate | 0.091 ± 0.014 h−1 | This study | |
| Species 2 growth rate | 0.186 ± 0.074 h−1 | This study | |
| Effect of plasmid carriage on species 1 growth rate | 0.73 ± 0.095 | This study | |
| Effect of plasmid carriage on species 2 growth rate | 0.85 ± 0.075 | This study | |
| Intraspecific conjugation rate in species 1 | 10−11 ± 0.2 cell−1⋅h−1 | This study | |
| Interspecific conjugation rate from species 1 to species 2 | 10−14 ± 0.11 cell−1⋅h−1 | This study | |
| Interspecific conjugation rate from species 2 to species 1 | 10−11.5 ± 0.32 cell−1⋅h−1 | This study | |
| Intraspecific conjugation rate in species 2 | 10−14 ± 0.4 cell−1⋅h−1 | This study | |
| Segregation rate | 1 × 10−4 h−1 | Refs. 24 and 26 | |
| Carrying capacity of species 1 | (6.01 ± 0.38) × 108 | This study | |
| Carrying capacity of species 2 | (1.1 ± 0.055) × 108 | This study | |
| Death rate | 0.009 h−1 | This study |
Fig. S1.
A wide range of plausible biological values for model parameters produce qualitatively similar model outcomes. To test the sensitivity of the models to different parameter estimates, the three models (no conjugation, intraspecific conjugation only, intraspecific and interspecific conjugation) were run with 1,000 different combinations of parameter values, each of which was drawn from a uniform distribution covering a wide range of values (≥1 SE in each direction). Each subpanel shows (the proportion of plasmid-carrying species 1) at the end of 5,000 iterations of the model, plotted against the values of each parameter. Gray dashed lines indicate the values used in the originally parameterized model. Each column of subpanels refers to a different parameter, and each row of panels corresponds to one of the different models. Note that for “no conjugation” and “intraspecific conjugation only,” the corresponding parameters were always fixed at zero. Points are colored according to (the proportion of plasmid-carrying species 2), with lighter shades of green indicating models where exceeded 1% of the population, and red indicating models where was below 10−8 (approaching zero). Inspection of the model outcomes shows that was strongly dependent on (species 1 intraspecific conjugation rate) and weakly dependent on (cost of plasmid carriage). was strongly dependent on (Fig. S2) and (interspecific conjugation rate from species 1 to species 2) and weakly dependent on .
Fig. S3.
Segregation rate affects qualitative model outcomes only at very high values. (A) To examine the sensitivity of the models to variation in plasmid segregation rate, we allowed segregation rates to vary between the species ( for species 1, for species 2), and the three models were run with 1,000 different combinations of different segregation rates for each species (from 10−6 to 10−0.5). Each panel shows at the end of 5,000 iterations of the model plotted against the values of each parameter. Note that is strongly dependent on , both with and without interspecific conjugation, but that this parameter does not affect plasmid survival unless it exceeds ∼10−2 h−1. (B) As in A, except the parameters are plotted against . Note the different scales between A and B y axes. As with Fig. S1, the plasmid goes extinct in species 2 without interspecific conjugation. With interspecific conjugation both and affect . However, the plasmid survives in species 2 even with high , provided is sufficiently low to allow plasmid survival in species 1.
Fig. 2.
A two-species model predicts between-species conjugation can promote plasmid carriage in an unfavorable host species. (A) Plasmid frequency in species 1 [P. fluorescens-like, , x-axis] and species 2 [P. putida-like, , y axis] was simulated over 5,000 iterations of a simple mass action plasmid dynamics model. The model was initiated with varying plasmid starting frequencies (0.1, 0.5, and 0.9). Arrows indicate the passage of time for each simulation, and a colored circle indicates the final state. Models omitting conjugation (gray) result in the loss of plasmid from both species. Models omitting interspecific conjugation (red) result in plasmid maintenance in species 1, but extinction in species 2, whereas models including interspecific conjugation (blue) result in plasmid maintenance at low levels in species 2. (B) Zoomed view of A. With interspecific conjugation, the plasmid is maintained at ∼0.35% in species 2.
Fig. S2.
Plasmid frequency in species 2 was strongly dependent on plasmid frequency in species 1 and the interspecific conjugation rate. (A) Endpoint plasmid frequencies from species 1 were plotted against endpoint frequencies species 2 for the 1,000 model simulation described in Fig. S1. Points are colored according to (interspecific conjugation rate from species 1 to species 2), except for one point in orange which shows the output of the originally parameterized model (Fig. 2). (B) Zoomed-in plot of A. Note that, even with low values of , the plasmid is present in species 2, provided it is maintained in species 1.
The mass action model is a simple approximation of the ecological system and hence excluded many details; most notably, the spatial structure inherent to soil. Therefore, to explicitly test the predicted importance of conjugation in plasmid maintenance, we ran short-term experiments using marked strains to follow the densities and plasmid status of bacteria beginning with (“donors”) and without pQBR57 (“recipients”). In single-species P. fluorescens populations (P. fluorescens donor and recipient, Fig. 3A), consistent with the cost of pQBR57, we found that donors were rapidly outcompeted by recipients and were not detected in any replicate by the end of the experiment (10 transfers). However, the plasmid was maintained in all replicates at ∼20–30% due to transfer into the recipient strain. These results, qualitatively consistent with the mass action model, show that pQBR57 survival in P. fluorescens, at least in the short term, was through conjugative transfer. To test whether cohabiting with plasmid-bearing P. fluorescens promoted plasmid carriage in P. putida, we cocultured recipient P. putida with donor P. fluorescens. Consistent with the model results, we found plasmid-bearing P. putida at low frequencies both during the experiment (three of six replicates) and at the end of the experiment (six of six replicates, Fig. 3B). Interestingly, despite beginning the experiment at a plasmid frequency of 100%, plasmid carriage in P. fluorescens was reduced to ∼25% by the end of the experiment, demonstrating the emergence of, and selection for, plasmid-free segregants. We also tested whether cohabiting with donor P. putida allowed pQBR57 invasion of a plasmid-free P. fluorescens recipient population. In all replicates, we detected plasmid-bearing P. fluorescens (Fig. 3C), and in two replicates, e and f, plasmid carriage by P. fluorescens reached frequencies sufficient for prolonged maintenance (as determined by comparison with Fig. 3A). In contrast, we saw marked plasmid loss from P. putida in all replicates due to competition from plasmid-free segregants. These data are therefore not consistent with an alternative hypothesis: that pQBR57 maintenance in P. putida in coculture was due to some other interspecific interaction (e.g., plasmid-borne genes that provide a selective advantage to P. putida only alongside P. fluorescens). Although mass action models are more commonly used to describe liquid cultures, our ability to capture the qualitative features seen in the soil microcosms is consistent with reports that spatial structure has little effect on plasmid transfer dynamics when donor and recipient bacteria encounter each other early in the growth cycle (17). Together, these results show that conjugative transfer underlies the invasion and maintenance of mobile resistance genes in a favorable bacterial host, and in so doing allows neighboring, unfavorable host species sustained access to those genes.
Fig. 3.
Short-term experiments show maintenance of pQBR57 by conjugation. (A) P. fluorescens donor and P. fluorescens recipient. Six replicate populations (columns, a–f) were initiated for each treatment. Each subpanel shows the densities at transfer of bacteria that began with pQBR57 (donors; dashed line) and bacteria that began without pQBR57 (recipients; solid line). The density of pQBR57+ is shown for the donors (filled yellow area below the dashed line) and the recipients (filled green area below the solid line). At the bottom of each subpanel, ticks indicate sampling points, green “+” symbols indicate detection of plasmid-bearing recipients, and a black circle indicates detection of plasmid-bearing recipients at the end of the experiment. (B) As in A, except the donor species was P. fluorescens and the recipient species was P. putida. The smaller subpanels below replicates b, c, and d show zoomed regions of the upper subpanels to indicate low-frequency pQBR57+ P. putida. (C) As in A, except with P. putida donor and P. fluorescens recipient.
Interspecific Plasmid Transfer Can Maintain Gene Mobility in Unfavorable Host Species.
In multispecies communities, favorable hosts could act as “sources” of plasmid for other community members. To explore the effects of a plasmid source on a neighboring species, we adapted our model for a single focal species by replacing the explicit interspecific conjugation term in Eqs. 1 and 2 with a rate constant , representing the sum of all interspecific conjugation events with an external (fixed) population. This gives Eqs. 3 and 4, allowing analytic progress (Supporting Information):
| [3] |
| [4] |
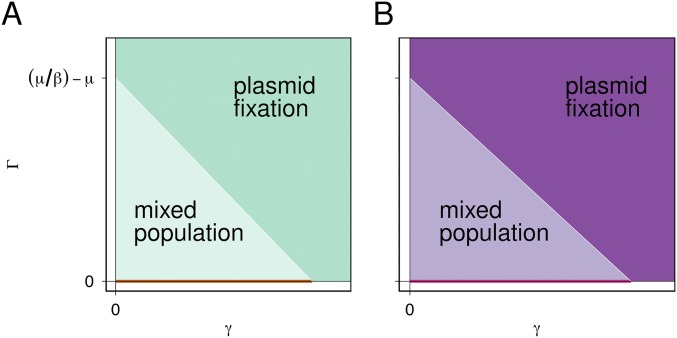
Without a plasmid source ( = 0), plasmid frequency in the focal species is determined primarily by the balance of the plasmid cost and the (intraspecific) conjugation rate. Under most parameter combinations, the plasmid either fixes or is completely lost, and with only a very narrow region of parameter space that results in a mixed population of plasmid-bearing and plasmid-free individuals (Fig. S4). Adding a plasmid source ( > 0) eliminates the region of parameter space in which the plasmid is absent from the focal species, and expands the region resulting in plasmid fixation in the focal species (Fig. S4). A plasmid source increases the effective conjugation rate for the focal species; in the simplified case where segregation is neglected, this increase is linear with the interspecific conjugation rate (Supporting Information).
Fig. S4.
A plasmid source enhances plasmid presence in a focal species. (A) Without selection, parameter space in which plasmids are lost (, orange), plasmids are fixed (, dark green), or a mixed population exists (, light green). Intraspecific conjugation is shown on the x axis, and conjugation from the source is on the y axis. Note that plasmids are only lost when . (B) With selection, parameter space in which plasmids are lost and replaced by chromosomal mutants (, orange), plasmids are fixed (, dark purple) or a mixed population exists (, light purple). The threshold for plasmid fixation (white line) both with and without selection is given by Eq. S3: . This consistency is reflected in the experiments; if the plasmid is expected to be maintained in the absence of selection, then we do not expect the invasion of chromosomal mutants when selection is applied, whereas if plasmid loss is anticipated without selection, then conditions favor the invasion of chromosomal mutants under selection. Segregation is mathematically neglected to produce these figures (Supporting Information), but some segregation events are presumed to occur in order for chromosomal mutants to lose the plasmids.
Next, we considered when plasmid-borne genes are under positive selection but can be captured by the chromosome at a low rate to produce chromosomal mutants, which benefit from the captured genes regardless of whether they also carry the plasmid. We expanded Eqs. 3 and 4 and added two further equations to describe plasmid-free and plasmid-bearing chromosomal mutants ( and , respectively) (25):
| [5] |
| [6] |
| [7] |
| [8] |
where represents selection against plasmid-free bacteria that do not have the beneficial genes (24). Similar to the case without positive selection, without a plasmid source the plasmid either remains at fixation in the focal species or is lost by competition with plasmid-free chromosomal mutants, with a narrow range of parameter values resulting in a mixed population of plasmid bearers and plasmid-free chromosomal mutants (Fig. S4). The addition of a plasmid source expands the region of parameter space that results in a mixed population in the focal species by inhibiting fixation of plasmid-free chromosomal mutants (Fig. S4). Therefore, the presence of a plasmid source in a microbial community is expected to greatly enhance persistence of plasmid-borne genes and maintenance of interspecific gene mobility.
Discussion
We have shown that coculture with an alternative host promoted the survival of a conjugative plasmid, maintaining community-wide access to the plasmid-borne gene pool. In single-species cultures, the plasmid invaded and was maintained by infectious conjugative transfer in one host (P. fluorescens), but was lost by segregation and purifying selection from the other (P. putida), regardless of whether its accessory genes were under selection. Coculture enabled a “source–sink” relationship in which interspecific transfer from the “source” host P. fluorescens maintained the plasmid in the “sink” host P. putida, preserving access to the accessory genes the plasmid carries. Long-term plasmid stability varies widely even between strains of the same species (26), but source–sink transfer dynamics mean that, if a conjugative plasmid is maintained in one member of a community, that member can become a plasmid source persistently infecting neighboring sink species. In natural communities, plasmid maintenance was found to correlate with existing plasmid prevalence, suggesting a tendency of certain hosts to preferentially act as plasmid sources (27). This dynamic, in which a subset of a multihost community is critical for persistence of an infectious element, is well studied in the context of disease reservoirs (12), and adapting theoretical and methodological approaches from disease reservoir ecology to plasmid biology could be productive, for example in identifying putative source species and understanding their role in the dissemination of important bacterial traits, like antibiotic resistance.
Potential plasmid recipients can stretch across diverse microbial groups (13), and although transconjugants within sink species may be transient (due to segregation or purifying selection) (28), their continual replenishment by conjugation from the source means that microbial community richness may be more robust to occasional bouts of selection for plasmid-borne genes. Coculture enhanced plasmid persistence in the sink species even under Hg(II) selection, whereas in single-species P. putida cultures, plasmid carriers tended to be outcompeted by mutants with chromosomal HgR. Plasmid survival under positive selection has important consequences because plasmids can carry many accessory genes (e.g., ref. 29), not all of which are selected at any given time. Interspecific conjugation also provides opportunity for plasmid recombination with resident genetic elements, enhancing genomic diversification (2). Furthermore, prolonged source–sink transfer dynamics could promote plasmid host range expansion (30), as also shown for bacteriophage (31). Previously, Dionisio et al. (32) noted how multispecies communities might accelerate plasmid spread when a highly conjugative intermediate species enhances plasmid transfer between two poorly conjugative species. In species-rich host communities, this “amplification effect” likely acts in concert with the source–sink transfer dynamic, with plasmid sources acting both as a conduit for rapid plasmid spread and a reservoir for long-term maintenance.
Conjugation rate rather than fitness cost explained differences in plasmid stability between the two pseudomonads. The plasmid was more readily lost from P. putida despite lower cost-of-carriage, presumably because less intraspecific conjugation meant plasmid-free individuals were less likely to be (re)infected. Because conjugation depends on population density as well as intrinsic conjugation rate (18), the higher density of P. fluorescens may also have enhanced plasmid spread. Increases in density over the course of the experiment, perhaps due to adaptation to the growth medium and/or transfer regime, may partly explain the reinvasion of pQBR57 in P. fluorescens in several populations between transfers 13 and 41. Mutations can increase conjugation rate (32, 33), and transient derepression of transfer gene expression following plasmid acquisition can also accelerate plasmid spread through naïve host populations (e.g., ref. 34), an effect particularly pronounced for bacteria growing on surfaces (17), although it is unclear whether either of these mechanisms are at work here. It is relevant that within-species conjugation underlies pQBR57 persistence in P. fluorescens, because the source–sink transfer dynamic would be unavailable to a plasmid that ameliorated its cost by completely abrogating conjugation (e.g., ref. 35). However, high conjugation rate is not essential for a plasmid source: hosts that achieve long-term plasmid stability through other routes, such as compensatory evolution (9, 36), could also become sources, provided they retain some degree of interspecific conjugation.
It is tempting to explain the persistence of plasmids and other mobile genetic elements by the benefits they bring to a bacterial community, for example as a communal gene pool (3) or by increasing robustness to environmental uncertainty (14). However, it is hard to envisage how selection might maintain mobile elements for the benefit of the community in the long term if they are costly for the individual cell in the short term (5). Our data show community-wide access to beneficial accessory genes resulting from processes occurring in one species in that community, specifically the persistence of a conjugative plasmid by infection. This extends previous evidence demonstrating the invasion and survival of plasmids as infectious parasitic elements, especially in spatially structured populations (11, 26, 37).
Detailed molecular and genetic studies of plasmid–host adaptation are revealing the mechanisms behind plasmid stability (7, 9, 35, 38, 39). However, these studies have primarily been conducted in one-plasmid/one-host systems, which are not reflective of natural microbial populations containing many different bacterial species (40) and mobile genetic elements (21, 41). We have shown that even simple two-species microbial communities offer evolutionary opportunities unavailable in a single-species population. In a diverse community, a few bacterial species acting as stable sources of conjugative plasmids may represent hubs of horizontal gene exchange. Identifying those species and understanding their ecology could have important implications for the control of clinically important mobile elements.
Materials and Methods
Bacterial Strains and Culture Conditions.
Pseudomonas fluorescens SBW25 and P. putida KT2440, labeled with gentamicin or streptomycin resistance markers and either plasmid-free or carrying pQBR57, were used for experiments (21). Soil microcosms were established and maintained similarly to previously described (21) and 1% (wt/vol) soil wash was transferred to a fresh microcosm every 4 d. Viable counts of each species were obtained by spreading samples on media containing species-selective antibiotics. For the first experiment, plasmid status in each species was assessed by PCR on ∼30 colonies using primers targeting plasmid loci and the merA gene (Supporting Information and Table S2). For the short-term experiment, we assessed plasmid status by replica plating onto Hg(II) plates and tested representative colonies by PCR. To test for HgR at the end of the experiments, we also spread samples on Hg(II) plates containing species-selective antibiotics and tested representative colonies by PCR. For the 16 µg/g treatment, we sampled up to 64 colonies. Because we tested approximately the same number of colonies from each species, differences in population size between the two species did not affect detection limits.
Table S2.
Oligonucleotide primers used in this study
| Primer name | Primer sequence | Target and purpose |
| pQBR57_TrfA_F | AGACGTGACCCTGGAATTGG | pQBR57_0001, identifying plasmid presence |
| pQBR57_TrfA_R | TGGTCGGATTTGAACCGTCG | |
| pQBR57_UvrD_F | CTTCGAAGCACACCTGATG | pQBR57_0131, identifying plasmid presence |
| pQBR57_UvrD_R | TGAAGGTATTGGCTGAAAGG | |
| Tn5042_MerA_F | TGCAAGACACCCCCTATTGGAC | merA, identifying presence of mercury reductase |
| Tn5042_MerA_R | TTCGGCGACCAGCTTGATGAAC | |
| KT2440_F | ATGGCAATGTCCGCAATCC | ISPpu10, identifying P. putida KT2440 (48) |
| KT2440_R | CGGAAGCCTCTGAACACG | |
| SBW25_F | ACTGCATTCAAAACTGACTGA | 16S DNA, identifying P. fluorescens SBW25 (49) |
| SBW25_R | AATCACACCGTGGTAACCG |
All PCRs were performed with the following thermocycling program: 5 min at 95 °C, followed by 30 cycles of 30 s at 95 °C, 30 s at 58 °C, and 1 min at 72 °C, followed by final extension for 5 min at 72 °C.
Analysis and Statistics.
For analysis of plasmid dynamics, we cropped data collected before transfer 7 because plasmid frequencies were dynamic due to short-term ecological processes [e.g., selection for HgR causing plasmid fixation in Hg(II) treatments]. Plasmid constancy was calculated using the fluctuation index (42) and analyzed by asymptotic Wilcoxon Mann–Whitney rank sum tests. To compare plasmid dynamics we used the R package “lme4” (43) to fit GLMMs with binomial response distributions and logit link functions (44, 45). For endpoint analyses, we compared populations using Fisher’s exact test. Full details and R code can be found in Supporting Information. Analyses were performed using R (R Foundation for Statistical Computing), and plots were created using “ggplot2” (46). For the mathematical models, parameters were estimated experimentally where possible (Supporting Information), numerical solutions were found using MATLAB (Mathworks), and analytic investigations were performed with the help of Mathematica (Wolfram).
Bacterial Strains and Culture Conditions
Pseudomonas fluorescens SBW25 and P. putida KT2440, labeled with gentamicin or streptomycin resistance markers using the mini-Tn7 transposon system and either plasmid-free or carrying pQBR57, were used for experiments (21). To control for effects of different markers, replicates ac used P. fluorescens GmR and P. putida SmR, whereas replicates d–f used P. fluorescens SmR and P. putida GmR. Individual colonies of each strain (one for each replicate) were isolated on selective King’s B (KB) agar and grown overnight at 28 °C in 6 mL of KB broth in a shaking incubator. Samples were resuspended in M9 buffer and mixed in approximately equal numbers according to treatment, diluted 1:10 with M9 buffer, and 100 µL used to initiate the experiment. Populations were cultured in soil microcosms consisting of 10 g of twice-autoclaved John Innes No. 2 potting soil supplemented with 900 µL of sterile H2O, or 900 µL of HgCl2 solution (giving a final concentration of 16 µg/g) and maintained at 28 °C at 80% relative humidity. The volumetric water content of the soil microcosms was ∼25%, i.e., damp but not saturated. Every 4 d, 10 mL of M9 buffer and 20 glass beads (5-mm diameter) were added to each population and mixed by vortexing for 1 min, and 100 µL of soil wash was transferred to fresh media. We calculated the number of generations in soil from the fact that 0.91% of the supernatant (100 µL from 10 mL plus 900 µL of H2O/HgCl2 solution plus 100 µL from the previous transfer) was passaged each transfer, and population densities at transfer were fairly consistent, indicating ∼6.78 generations per transfer on average (6.78 × 65 = 440.78 generations in total). Population density at transfer varied between populations (Fig. 1), so this value should be regarded as a best estimate. Furthermore, nutrients released during soil sterilization may have increased the growth rate of Pseudomonas in our soil microcosms—rates may be lower in the presence of an established natural community.
At certain transfers, supernatant was diluted and spread on selective KB agar for viable counts. For the first experiment, plasmid status was assessed at 17 points (every odd-numbered transfer from transfer 1–17, and then every six transfers to transfer 65) by performing multiplex colony PCR on ∼30 randomly selected colonies from each species from each population using primers targeting two plasmid loci (PQBR57_0001 and PQBR57_0131) and the merA gene (Table S2). This gives a >95% chance of detecting a genotype constituting 10% or more of the population. For the short-term experiment, we assessed plasmid status by replica plating onto KB with 100 µM HgCl2 and tested representative colonies by PCR. Consistent with the long-term experiment, no pQBR57– merA+ colonies were found in the short-term experiment. To test for the presence of HgR at the end of the experiments, we also spread samples on selective KB with 20 µM HgCl2 and tested representative colonies by PCR. Dilution factors were adjusted so approximately the same number of colony-forming units of each species were tested, giving approximately a >95% chance of detecting plasmid bearers constituting >0.06% of the population. For the 16 µg/g treatment, we sampled up to 64 colonies to test for plasmid presence, which gives a >95% chance of detecting plasmid bearers constituting >4.7% of the population.
Testing for P. putida Acquisition of pQBR57 Following Extraction from the Soil Microcosm
To test whether the pQBR57+ P. putida isolates obtained from the coculture experiments could have acquired pQBR57 from P. fluorescens following extraction from the soil, we grew separate soil microcosm cultures (n = 3) of pQBR57+ P. fluorescens GmR, pQBR57+ P. fluorescens SmR, plasmid-free P. putida GmR, and plasmid-free P. putida SmR for 96 h. Samples were retrieved as described above, diluted, and mixed 1:1 pQBR57+ P. fluorescens GmR with plasmid-free P. putida SmR, and pQBR57+ P. fluorescens SmR with plasmid-free P. putida GmR. Samples were spread on KB agar plates supplemented with appropriate antibiotics as described for the long-term experiment. Forty-seven randomly selected P. putida colonies were isolated from each sample (282 in total) and screened for plasmid carriage as described above. No plasmid-bearing colonies were detected, indicating that the incidents of pQBR57+ P. putida detected in the experiments were most likely carrying the plasmid in situ.
Explicit Source–Sink Model
The source–sink model is defined by Eqs. 1 and 2. If we neglect segregation, then the analytic solution can be described as follows. The equations become the following:
| [S1] |
| [S2] |
with the parameters described in the main text. The nullclines for the system are given by the algebraic relations when these equations are set to zero. Eq. S1 shows that either the plasmid is fixed ( or the solutions lie on the line . Eq. S2 is not so simple, giving a quadratic relationship between the points. This gives four fixed points for the system:
where is derived from using the linear relation in the paragraph above and is given by the following:
where is always negative and unphysical.
Of interest is the transition from a stable interior point solution to the fixed point corresponding to plasmid fixation, becoming stable. This can be deduced by the equality or more simply by examining the Jacobian matrix of the equations above evaluated at . This analysis demonstrates that plasmid fixation occurs at a line of transcritical bifurcations in the plane given by the following:
| [S3] |
which is depicted in Fig. S4. A Mathematica worksheet (Halletal.SInb1.nb) is included with the solutions of this equation.
If segregation is neglected, the analytic model solution predicts a simple plasmid conjugation rate/growth rate trade-off for which a mixed fixed point only occurs in a small interval [when ] in the absence of a source. With a source, the plasmid can never be eliminated entirely, and the inequality (Eq. S3) applies. If segregation is not neglected, then the system becomes difficult to analyze exactly as fixed points from Eq. S1 no longer have a simple factor, . The relevant nullclines are now a quadratic form and a modified quadratic respectively in the space. However, the qualitative dynamics are largely unchanged; segregation acts to move the fixed point for plasmid fixation slightly away from the axis due to the transient presence of plasmid-free bacteria due to segregation events. A Mathematica worksheet (Halletal.SInb2.nb) is included, exploring these effects of segregation. We have previously established (20) that segregation rates need to approach the order of the growth rates to induce a change in qualitative dynamics, which is significantly beyond any plausible biological estimates.
Mathematica worksheets can be found at Dryad Digital Repository (dx.doi.org/10.5061/dryad.488dk).
Estimation of Model Parameters
and (growth rates in per hour and carrying capacities in colony-forming units per gram) were estimated for both species by destructively sampling cocultured populations of P. fluorescens and P. putida grown in soil microcosms. Specifically, replicate cultures (n = 3) of either plasmid-free P. fluorescens SBW25 GmR or P. putida KT2440 SmR were grown overnight in 6 mL of KB broth at 28 °C in a shaking incubator, resuspended in M9 buffer, mixed in approximately equal numbers (for coculture treatment), or diluted to an equivalent number of colony-forming units per milliliter (for single-species treatment), diluted 1:10 with M9 buffer, and 100 µL used to inoculate 10 g of twice-autoclaved John Innes No. 2 potting soil supplemented with 900 µL of sterile H2O. Fifteen microcosms were set up for each treatment and maintained at 28 °C at 80% relative humidity. One, 12, 24, 48, and 96 h after inoculation, three microcosms from each treatment were sampled, and viable counts were obtained as described above. A logistic curve [), where is the density at time and is the starting density] was fitted to data from each treatment using nonlinear least squares (the “nls” function in R), and and were extracted for each species both alone and in coculture. We did not detect variation in either nor within species between coculture and single-species cultures [ : effect of coculture P. fluorescens F(1,26) = 0.35, P = 0.56; P. putida F(1,26) = 1.13, P = 0.3. : t test comparing densities at 96-h P. fluorescens t(2.5) = 2.0176, P = 0.172; P. putida t(3.89) = −0.11, P = 0.92]. However, both and varied significantly between species [ : effect of species F(1,26) = 196.2, P < 0.001; : t test comparing densities at 96-h t(2.085) = 12.9, P = 0.005].
(growth rate of plasmid-carrying bacteria in per hour) were estimated for each species by multiplying the species-specific growth rates by the fitness of plasmid-bearing bacteria relative to plasmid-free.
Relative fitness assays in soil microcosms were performed as described by Hall et al. (21), except microcosms were preconditioned with either 0 or 16 µg/g Hg(II) as described above and were inoculated with 100 µL of competition mix, made up of 1:1 mixture of GmR and SmR competitors diluted 1:10 with M9 salts. For each species, we measured the fitness of GmR plasmid-free relative to SmR plasmid-free, GmR plasmid-free relative to SmR pQBR57+, and GmR pQBR57+ relative to SmR plasmid-free, in quadruplicate. We counted GmR and SmR competitors by replica plating onto KB containing the appropriate antibiotic. Relative fitness for the GmR competitor was calculated as W, the ratio of Malthusian growth parameters []. To compensate for the effects of different antibiotic markers we calculated the change in fitness caused by plasmid carriage by dividing each measurement by the mean relative fitness of plasmid-free control competitions (, where was the fitness calculated from the ith competition in species and was the mean fitness of plasmid-free species ), and, for cases where the plasmid was in the SmR strain, taking the reciprocal to get the fitness of pQBR57+ relative to plasmid-free. For each species, the resulting values were averaged to give and . was found to vary significantly between species [t(13.3) = −2.7928, P = 0.015].
, , , and (conjugation rates in grams per cell per hour) were estimated using the endpoint method as described by Hall et al. (21). Rates were measured for each combination of donor (P. fluorescens or P. putida), recipient, and donor antibiotic resistance marker (GmR or SmR). We found that conjugation rate varied significantly with recipient, with rates ∼1,000× higher when the plasmid was transferred to P. fluorescens [linear model, effect of recipient F(1,16) = 238.2, P < 0.001]. We also found significant effects of the marker in P. putida [effect of recipient:marker F(1,16) = 12.62, P < 0.005; effect of donor:recipient:marker F(1,16) = 18.18, P < 0.001], with apparent conjugation rates being almost 100× greater when the plasmid was transferred from GmR P. putida to SmR P. putida. This was probably due to a slight difference in growth rates between our marked P. putida lines, which becomes apparent when they are grown in competition with one another. To obtain conjugation rate parameters, we therefore averaged over markers. For accurate measurements of conjugation rate, the endpoint method requires that transfer rates between donors and recipients and between transconjugants and recipients are similar (32). This assumption is probably not fulfilled for our estimates of interspecific conjugation because intraspecific conjugation within P. fluorescens is ∼1,000× greater than intraspecific conjugation within P. putida, meaning that it is likely our interspecific conjugation rate from P. putida to P. fluorescens () is an overestimate. However, we found that varying this parameter value by several orders of magnitude did not affect the qualitative model predictions (e.g., Fig. S1).
(segregation rates in per cell per hour) were not experimentally estimated for this system for technical reasons, although we did observe segregants from both species (e.g., Fig. 3). Instead, to examine the role of this parameter, we varied over a wide range of biologically plausible values for each species (24, 26) while holding the other parameters at their estimated values (Fig. S3). Consistent with the analyses described above, we found that the value of has very little qualitative impact on the mathematical results until it reaches biologically implausible high values.
, (death rate per hour), was estimated by dividing the proportion of each culture’s supernatant that was discarded every transfer (0.99) by the number of hours between each transfer (96 h). All model parameters and their associated errors are shown in Table S1.
Analysis and Statistics
For analysis of plasmid dynamics, we cropped data collected before transfer 7 (day 28) because plasmid frequencies were dynamic due to short-term ecological processes [e.g., selection for HgR causing plasmid fixation in Hg(II) treatments]. To compare plasmid dynamics between single-species and coculture treatments, we used the R package “lme4” to fit generalized linear mixed-effects models (GLMMs) with binomial response distributions and logit link functions. GLMMs are a powerful way of analyzing hierarchically structured data in which the response variable is bounded and which therefore do not meet the assumptions of linear mixed-effect models (44, 45). We analyzed each combination of species and mercury treatment separately. We initially fitted “beyond optimal” (44) models with transfer, culture treatment (i.e., with or without other species), marker, and their interactions as fixed effects. To achieve model convergence, “transfer” was centered by subtracting median transfer from each value. We included population as a random effect on intercept and slope to account for repeated measures. The response variable was the number of plasmid-positive clones, weighted by the number of clones tested. To account for overdispersion, we added an observation-level random effect (45, 47); similar results were obtained by using the R package glmmADMB to fit a GLMM with a beta-binomial response distribution (47). We identified the optimal model by comparing nested models using an information criterion (Akaike’s information criterion) approach; in no cases did we detect any significant interactions involving marker, consistent with expectations. We tested fixed effects by parametric bootstrapping (45), i.e., comparing the observed deviance [change in –2 log-likelihood between the reduced (null) model and the full model] with a deviance distribution generated by repeatedly fitting models to data simulated using the reduced model. We found these results broadly consistent with likelihood ratio testing and information criterion approaches. For endpoint analysis, we compared the number of populations in which the plasmid survived or went extinct using Fisher’s exact test. Analyses and data can be found at Dryad Digital Repository (dx.doi.org/10.5061/dryad.488dk).
Acknowledgments
We thank V. Friman and J. Pitchford for comments. This work was supported by ERC Consolidator Grant Agreement 311490-COEVOCON (to M.A.B.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data and analysis reported in this paper have been deposited in the Dryad Digital Repository (dx.doi.org/10.5061/dryad.488dk).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1600974113/-/DCSupplemental.
References
- 1.Frost LS, Leplae R, Summers AO, Toussaint A. Mobile genetic elements: The agents of open source evolution. Nat Rev Microbiol. 2005;3(9):722–732. doi: 10.1038/nrmicro1235. [DOI] [PubMed] [Google Scholar]
- 2.Halary S, Leigh JW, Cheaib B, Lopez P, Bapteste E. Network analyses structure genetic diversity in independent genetic worlds. Proc Natl Acad Sci USA. 2010;107(1):127–132. doi: 10.1073/pnas.0908978107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Norman A, Hansen LH, Sørensen SJ. Conjugative plasmids: Vessels of the communal gene pool. Philos Trans R Soc Lond B Biol Sci. 2009;364(1527):2275–2289. doi: 10.1098/rstb.2009.0037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baltrus DA. Exploring the costs of horizontal gene transfer. Trends Ecol Evol. 2013;28(8):489–495. doi: 10.1016/j.tree.2013.04.002. [DOI] [PubMed] [Google Scholar]
- 5.Bergstrom CT, Lipsitch M, Levin BR. Natural selection, infectious transfer and the existence conditions for bacterial plasmids. Genetics. 2000;155(4):1505–1519. doi: 10.1093/genetics/155.4.1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stewart FM, Levin BR. The population biology of bacterial plasmids: A priori conditions for the existence of conjugationally transmitted factors. Genetics. 1977;87(2):209–228. doi: 10.1093/genetics/87.2.209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Harrison E, Brockhurst MA. Plasmid-mediated horizontal gene transfer is a coevolutionary process. Trends Microbiol. 2012;20(6):262–267. doi: 10.1016/j.tim.2012.04.003. [DOI] [PubMed] [Google Scholar]
- 8.San Millan A, et al. Positive selection and compensatory adaptation interact to stabilize non-transmissible plasmids. Nat Commun. 2014;5:5208. doi: 10.1038/ncomms6208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Harrison E, Guymer D, Spiers AJ, Paterson S, Brockhurst MA. Parallel compensatory evolution stabilizes plasmids across the parasitism-mutualism continuum. Curr Biol. 2015;25(15):2034–2039. doi: 10.1016/j.cub.2015.06.024. [DOI] [PubMed] [Google Scholar]
- 10.Sengupta M, Austin S. Prevalence and significance of plasmid maintenance functions in the virulence plasmids of pathogenic bacteria. Infect Immun. 2011;79(7):2502–2509. doi: 10.1128/IAI.00127-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bahl MI, Hansen LH, Sørensen SJ. Impact of conjugal transfer on the stability of IncP-1 plasmid pKJK5 in bacterial populations. FEMS Microbiol Lett. 2007;266(2):250–256. doi: 10.1111/j.1574-6968.2006.00536.x. [DOI] [PubMed] [Google Scholar]
- 12.Viana M, et al. Assembling evidence for identifying reservoirs of infection. Trends Ecol Evol. 2014;29(5):270–279. doi: 10.1016/j.tree.2014.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Klümper U, et al. Broad host range plasmids can invade an unexpectedly diverse fraction of a soil bacterial community. ISME J. 2015;9(4):934–945. doi: 10.1038/ismej.2014.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Heuer H, Smalla K. Plasmids foster diversification and adaptation of bacterial populations in soil. FEMS Microbiol Rev. 2012;36(6):1083–1104. doi: 10.1111/j.1574-6976.2012.00337.x. [DOI] [PubMed] [Google Scholar]
- 15.Hall-Stoodley L, Costerton JW, Stoodley P. Bacterial biofilms: From the natural environment to infectious diseases. Nat Rev Microbiol. 2004;2(2):95–108. doi: 10.1038/nrmicro821. [DOI] [PubMed] [Google Scholar]
- 16.Kim HJ, Boedicker JQ, Choi JW, Ismagilov RF. Defined spatial structure stabilizes a synthetic multispecies bacterial community. Proc Natl Acad Sci USA. 2008;105(47):18188–18193. doi: 10.1073/pnas.0807935105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simonsen L. Dynamics of plasmid transfer on surfaces. J Gen Microbiol. 1990;136(6):1001–1007. doi: 10.1099/00221287-136-6-1001. [DOI] [PubMed] [Google Scholar]
- 18.Krone SM, Lu R, Fox R, Suzuki H, Top EM. Modelling the spatial dynamics of plasmid transfer and persistence. Microbiology. 2007;153(Pt 8):2803–2816. doi: 10.1099/mic.0.2006/004531-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gómez P, Buckling A. Bacteria-phage antagonistic coevolution in soil. Science. 2011;332(6025):106–109. doi: 10.1126/science.1198767. [DOI] [PubMed] [Google Scholar]
- 20.Cho JC, Tiedje JM. Biogeography and degree of endemicity of fluorescent Pseudomonas strains in soil. Appl Environ Microbiol. 2000;66(12):5448–5456. doi: 10.1128/aem.66.12.5448-5456.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hall JPJ, et al. Environmentally co-occurring mercury resistance plasmids are genetically and phenotypically diverse and confer variable context-dependent fitness effects. Environ Microbiol. 2015;17(12):5008–5022. doi: 10.1111/1462-2920.12901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hill KEM, Top E. Gene transfer in soil systems using microcosms. FEMS Microbiol Ecol. 1998;25(4):319–329. [Google Scholar]
- 23.Li P, Feng XB, Qiu GL, Shang LH, Li ZG. Mercury pollution in Asia: A review of the contaminated sites. J Hazard Mater. 2009;168(2-3):591–601. doi: 10.1016/j.jhazmat.2009.03.031. [DOI] [PubMed] [Google Scholar]
- 24.Harrison E, et al. Bacteriophages limit the existence conditions for conjugative plasmids. MBio. 2015;6(3):e00586. doi: 10.1128/mBio.00586-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Svara F, Rankin DJ. The evolution of plasmid-carried antibiotic resistance. BMC Evol Biol. 2011;11(1):130. doi: 10.1186/1471-2148-11-130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.De Gelder L, Ponciano JM, Joyce P, Top EM. Stability of a promiscuous plasmid in different hosts: No guarantee for a long-term relationship. Microbiology. 2007;153(Pt 2):452–463. doi: 10.1099/mic.0.2006/001784-0. [DOI] [PubMed] [Google Scholar]
- 27.Bellanger X, Guilloteau H, Breuil B, Merlin C. Natural microbial communities supporting the transfer of the IncP-1β plasmid pB10 exhibit a higher initial content of plasmids from the same incompatibility group. Front Microbiol. 2014;5(637):637. doi: 10.3389/fmicb.2014.00637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yano H, et al. Host range diversification within the IncP-1 plasmid group. Microbiology. 2013;159(Pt 11):2303–2315. doi: 10.1099/mic.0.068387-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sen D, et al. Broad-host-range plasmids from agricultural soils have IncP-1 backbones with diverse accessory genes. Appl Environ Microbiol. 2011;77(22):7975–7983. doi: 10.1128/AEM.05439-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kottara A, Hall JPJ, Harrison E, Brockhurst MA. Multi-host environments select for host-generalist conjugative plasmids. BMC Evol Biol. 2016;16(1):70. doi: 10.1186/s12862-016-0642-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Benmayor R, Hodgson DJ, Perron GG, Buckling A. Host mixing and disease emergence. Curr Biol. 2009;19(9):764–767. doi: 10.1016/j.cub.2009.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dionisio F, Matic I, Radman M, Rodrigues OR, Taddei F. Plasmids spread very fast in heterogeneous bacterial communities. Genetics. 2002;162(4):1525–1532. doi: 10.1093/genetics/162.4.1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.De Gelder L, Williams JJ, Ponciano JM, Sota M, Top EM. Adaptive plasmid evolution results in host-range expansion of a broad-host-range plasmid. Genetics. 2008;178(4):2179–2190. doi: 10.1534/genetics.107.084475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lundquist PD, Levin BR. Transitory derepression and the maintenance of conjugative plasmids. Genetics. 1986;113(3):483–497. doi: 10.1093/genetics/113.3.483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Turner PE, et al. Antibiotic resistance correlates with transmission in plasmid evolution. Evolution. 2014;68(12):3368–3380. doi: 10.1111/evo.12537. [DOI] [PubMed] [Google Scholar]
- 36.Dahlberg C, Chao L. Amelioration of the cost of conjugative plasmid carriage in Eschericha coli K12. Genetics. 2003;165(4):1641–1649. doi: 10.1093/genetics/165.4.1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fox RE, Zhong X, Krone SM, Top EM. Spatial structure and nutrients promote invasion of IncP-1 plasmids in bacterial populations. ISME J. 2008;2(10):1024–1039. doi: 10.1038/ismej.2008.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.San Millan A, Toll-Riera M, Qi Q, MacLean RC. Interactions between horizontally acquired genes create a fitness cost in Pseudomonas aeruginosa. Nat Commun. 2015;6:6845. doi: 10.1038/ncomms7845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Loftie-Eaton W, et al. Evolutionary paths that expand plasmid host-range: Implications for spread of antibiotic resistance. Mol Biol Evol. 2016;33(4):885–897. doi: 10.1093/molbev/msv339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lozupone CA, Knight R. Global patterns in bacterial diversity. Proc Natl Acad Sci USA. 2007;104(27):11436–11440. doi: 10.1073/pnas.0611525104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sentchilo V, et al. Community-wide plasmid gene mobilization and selection. ISME J. 2013;7(6):1173–1186. doi: 10.1038/ismej.2013.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vogwill T, Fenton A, Brockhurst MA. Dispersal and natural enemies interact to drive spatial synchrony and decrease stability in patchy populations. Ecol Lett. 2009;12(11):1194–1200. doi: 10.1111/j.1461-0248.2009.01374.x. [DOI] [PubMed] [Google Scholar]
- 43.Bates D, Mächler M, Bolker B, Walker S. Fitting linear mixed-effects models using lme4. J Stat Softw. 2014;67(1):1–48. [Google Scholar]
- 44.Zuur A, Ieno EN, Walker N, Saveliev AA, Smith GM. Mixed Effects Models and Extensions in Ecology with R. Springer Science and Business Media; New York: 2009. [Google Scholar]
- 45.Bolker BM, et al. Generalized linear mixed models: A practical guide for ecology and evolution. Trends Ecol Evol. 2009;24(3):127–135. doi: 10.1016/j.tree.2008.10.008. [DOI] [PubMed] [Google Scholar]
- 46.Wickham H. ggplot2: Elegant Graphics for Data Analysis. Springer; New York: 2010. [Google Scholar]
- 47.Harrison XAA. A comparison of observation-level random effect and Beta-Binomial models for modelling overdispersion in Binomial data in ecology & evolution. PeerJ. 2015;3:e1114. doi: 10.7717/peerj.1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ramos-González MI, Campos MJ, Ramos JL, Espinosa-Urgel M. Characterization of the Pseudomonas putida mobile genetic element ISPpu10: An occupant of repetitive extragenic palindromic sequences. J Bacteriol. 2006;188(1):37–44. doi: 10.1128/JB.188.1.37-44.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Scarpellini M, Franzetti L, Galli A. Development of PCR assay to identify Pseudomonas fluorescens and its biotype. FEMS Microbiol Lett. 2004;236(2):257–260. doi: 10.1016/j.femsle.2004.05.043. [DOI] [PubMed] [Google Scholar]