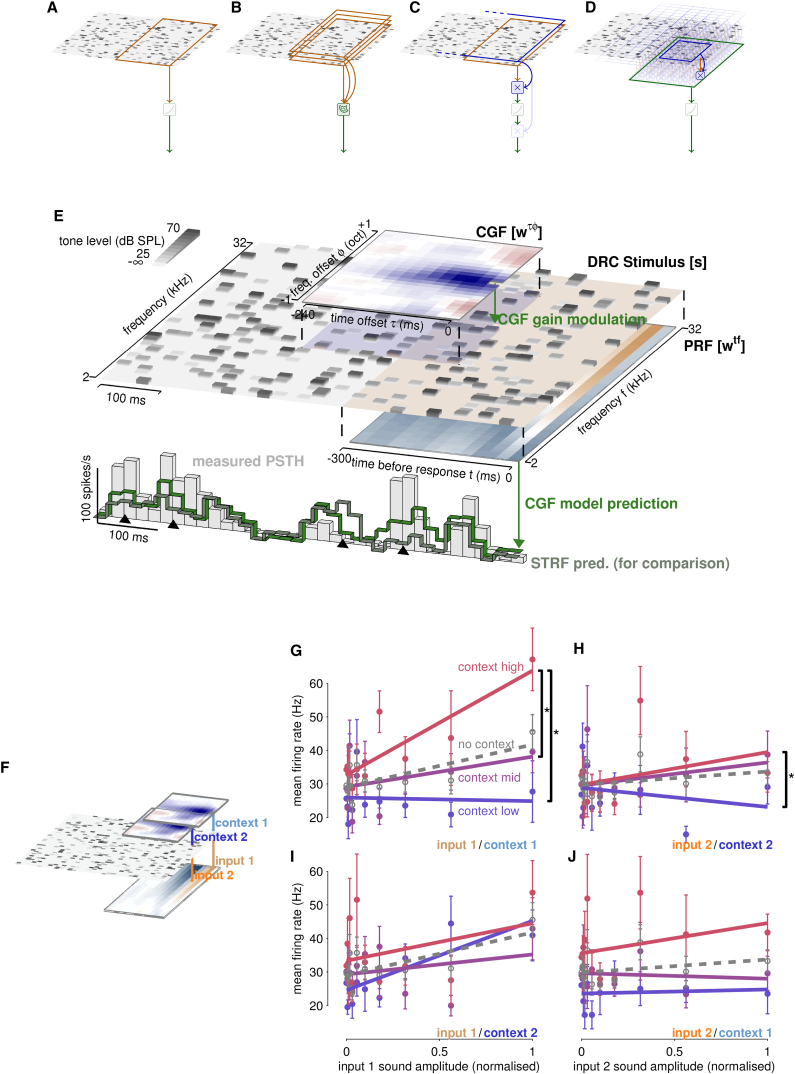
Figure 1.
Local Context Shapes Input-Specific Gain
(A–D) Cartoon illustrations of receptive field integration mechanisms.
(A) In the most basic scheme, input stimuli (gray-level spectrogram) are integrated by a single set of fixed weights (orange). Pointwise nonlinear transforms may apply to each specific input (not shown) or to the integrated weights (light green).
(B) Multidimensional LNP models include a small number of differently weighted overlapping integration fields, with outputs combined by a multi-imensional nonlinearity (green). Methods such as MID and STC are designed to characterize such models.
(C) Normalization, or other variable global gain, involves the output of one field (blue) modulating the gain of the integrated response to the other (orange). The normalization field may extend well beyond the integration field, so that the effective gain reflects global statistical properties of the stimulus. A further nonlinear transformation (light green) may act before or after gain modulation (light blue).
(D) In the phenomenon described here, local context (blue) around each input shapes the gain of response to that specific input. Each input experiences a different context and thus a potentially different gain. Gain-modulated inputs are integrated (green), with a possible further nonlinear transformation (light green).
(E) The CGF model. The contextual input-specific gain model incorporates two sets of time-freqency weights. The Principal Receptive Field (PRF; ) describes the basic sensitivity of the neuron to spectrotemporal energy at all frequencies within a short time window, analogous to the STRF. The Contextual Gain Field (CGF; ) describes how each sensitivity is modified by its local acoustic context. The model can be viewed as acting in two stages. First, the stimulus spectrogram is convolved with the CGF in both time and frequency to estimate the local input-specific gain at each spectrotemporal point (upper green arrow). The local stimulus power is then scaled by the corresponding gain and these scaled values, weighted by the PRF, are summed to model the neural response (lower green arrow). The measured response (peri-stimulus-time histogram or PSTH) for one example cortical neuron is shown (gray bars) along with the rates predicted by the CGF model (bright green) and an unmodified STRF (dull gray-green). Differences in prediction (black triangles) show that local contextual gain effects both increase and decrease firing rates relative to the STRF model of static sensitivities.
(F–J) Local input-specificity of contextual gain effects. The relationships between the measured responses of one example unit and the sound level at two spectrotemporal locations within the unit’s PRF far enough apart in time and frequency to be subject to different local sound contexts (F) are shown without reference to local context (gray open circles and dashed lines); sorted by whether the integrated contextual energy in a local window around that spectrotemporal location fell within a low, middle or high quantile (G and H, colored circles and lines); or, as a control, sorted according to “distant” contextual energy — i.e., integrated energy around the other of the two input locations (I and J, colored circles and lines). Error bars indicate standard error in the mean; lines are fit to the empirical data. The slopes of the input-response relationships differ when sorted by local spectrotemporal context (black bars with asterisks indicate significance), but not when sorted by contextual energy at the spectrotemporally distant location.