Scientific Review of Phase I Protocols With Novel Dose-Escalation Designs: How Much Information Is Needed?

INTRODUCTION

The standard design of phase I dose-escalation trials in oncology has been the 3 + 3 design, and its modifications and performance are well understood.^1,2 This design was favored, in part, because escalation is cautious, and the risk of overdosing the patient is thought to be limited. For cytotoxic drugs, in general, greater toxicity and efficacy will occur at progressively higher dose levels; dose-limiting toxicities (DLTs) determine the maximum-tolerated dose (MTD), and the number of dose levels is typically limited to five or six. However, the standard design can take more levels, and therefore more patients, to identify the MTD and may still underestimate it.² This fact is particularly relevant for today's targeted agents. To improve trial efficiency, minimize the number of treated patients, and contain the cost of drug development, alternative approaches to phase I drug development using model-based dose-escalation designs have evolved.

Model-based dose-escalation designs and, more generally, adaptive designs have become popular and are based on the idea of constantly updating the estimated toxicity rates based on new safety data. These designs can also bridge information from an apparently heterogeneous group of patients to a more homogeneous group defined by specific biomarkers.³ Thus, they are increasingly used to improve phase I trial efficiency by aggregating information across groups (eg, multiple disease sites), thereby enabling investigators to treat fewer patients to estimate the MTD.

However, the methodology of these complex adaptive dose-finding designs for early-phase studies can be difficult to understand. In our experience, the lengthy, technical statistical language that accompanies these protocols often presents a challenge to the clinical investigators who participate in these trials or serve on institutional scientific review committees, leaving the responsibility for scientific review solely to the biostatistician. In addition, we have sometimes found that the methods in some protocols are technically incomplete or include techniques that have not been formally established through statistical methodologic research. Navigating the statistical design complexities during the review process can, at a minimum, result in protocol activation delays or, more seriously, expose patients to unnecessary risk. In this article, we discuss some of the challenges that we have encountered in the review of phase I trials and provide recommendations for essential statistical elements required to adequately review the validity and safety of novel dose-escalation designs.

Model-Based Dose-Escalation Designs

Tuning parameters.

Phase I designs have several clinical parameters such as a prespecified window of DLT observation, what types of adverse events define DLT, and design parameters that include cohort size, safety stopping rules, and a predetermined safety threshold (eg, 33% or below). Model-based dose-escalation designs generally rely on one or more tuning parameters to guide the dose escalation. One tuning parameter is the presumed dose-toxicity relationship (called the “initial curve”) for the experimental agent. As toxicity information becomes available, the presumed dose-toxicity relationship will be updated through the course of the trial (“tuned”) by combining it with actual data arising from the treatment of patients on the trial by using an updating scheme, which results in an updated curve. Although each successive decision to escalate (or de-escalate) is based on the most recent data, the initial presumed dose-toxicity relationship continues to play a role in these decisions because it is included in the calculation of the update. Hence, the initial pretreatment choice influences subsequent decisions throughout the conduct of the study, although that influence diminishes over time as more data accumulate. Other tuning parameters might include prior information, which could reflect information from historical data such as completed studies. The prior information informs the dose escalation early on in the trial in the absence of any safety data obtained from the ongoing study. Tuning parameters must be specified at the time the protocol is written and before any patients are enrolled, because their choice affects subsequent decisions.^4,5 Investigators can choose tuning parameters that lead to either conservative dose escalations and more treated patients or more aggressive dose escalations and fewer treated patients.

Operating characteristics.

The operating characteristics of a trial are the statistical estimates of the expected number of DLTs at each dose level, the expected number of patients who may be overdosed, and the proportion of trials under which the MTD is correctly identified. The operating characteristics are dependent on the choice of the tuning parameters. Because of the nature of the adaptive design, operating characteristics can be evaluated only through simulations that predict how pretrial tuning parameters are updated by accumulating clinical trial data. In the traditional 3 + 3 design, dose escalation depends on the information gained from the treatment of the most recent three or six patients. In adaptive designs, the operating characteristics are obtained only through simulations of hypothetical patients being treated at escalating doses under various assumed true dose-toxicity curves. The operating characteristics provide insight into how a particular design will perform in terms of safety and accuracy. Along with tuning parameters, a clear description of the trial's operating characteristics is required for independent reviewers to assess the integrity of phase I trial designs.

Examples

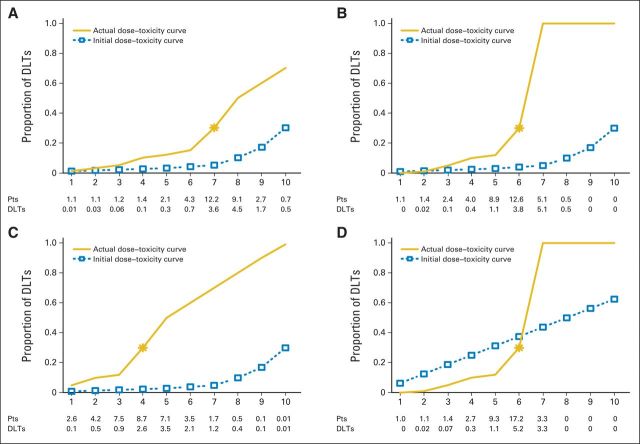
Any design's performance depends on the actual true underlying dose-toxicity curve, which we do not know in practice. For this reason, we need to evaluate a design under various assumed true dose-toxicity curves (referred to here as scenarios), and the performance of the design must be clinically acceptable under all or most scenarios. The operating characteristics can indicate examples that are either clinically acceptable or potentially not acceptable. If we find, under a clinically plausible scenario, that the design is too aggressive, then we need to change the tuning parameters to make the design less aggressive. In Figure 1, we provide four examples of trial designs with different tuning parameters and/or assumed dose-toxicity curves and show the operating characteristics based on simulations of 1,000 hypothetical trials.

Fig 1.

Operating characteristics for hypothetical dose-toxicity curves and initial dose-toxicity curves in a trial design with 10 dose levels. The initial curve (dashed line) is what the model relies on as a starting assumption (tuning parameter), whereas the accumulated data override this initial curve and fine tune the location of the MTD based on an adaptive re-estimation. Actual dose-toxicity curve (solid line) is the true underlying dose-toxicity curve that is unknown at the design stage. Trial designs (A) 1, (B), 2, (C) 3, and (D) 4, as listed in Table 1. DLT, dose-limiting toxicity; Pts, patients.

In trial design 1 (Fig 1A), the presumed dose-toxicity relationship curve is an initially flat then steadily rising curve (dashed line) favoring the highest level as MTD dose (level 10). An assumed true dose-toxicity curve, which is unknown when we design the trial, shows that dose level 7 is the MTD. By using the assumed true dose-toxicity curve, simulations predict that 12 to 13 of the first 23 to 24 hypothetical trial patients (Fig 1A) will be treated at the MTD (dose 7) and, of these, three to four will experience a DLT. The operating characteristics also show the number of potential patients treated and the number of expected DLTs at each of the 10 planned dose levels. In this particular trial design, the operating characteristics determine that, on average, 13 patients would be treated above the MTD and about half would experience a DLT. This simulation suggests that this design is too aggressive. Although the parameters chosen in this design would find the MTD accurately, half the patients treated above the MTD will have a DLT. Table 1 shows that 56% of the simulated trials with this design selected the right MTD, which is level 7.

Table 1.

Operating Characteristics of a Trial Based on 1,000 Simulated Hypothetical Trials

Trial Design	Dose Levels
	1	2	3	4	5	6	7	8	9	10
Trial design 1
Initial curve A	0.01	0.015	0.02	0.025	0.03	0.04	0.05	0.10	0.17	0.30
Dose toxicity curve 1	0.01	0.03	0.05	0.1	0.12	0.15	0.3	0.5	0.6	1
Accuracy (percentage of trials)	0	0	0	0.7	2.5	17	56	23	1	0
Allocation (No. of patients)	1.1	1.1	1.2	1.4	2.1	4.3	12.2	9.1	2.7	0.7
Percentage of patients	3	3	3	4	6	12	34	25	8	2
Safety (No. of patients with DLTs)	0.01	0.03	0.06	0.13	0.27	0.66	3.6	4.5	1.7	0.5
Trial design 2
Initial curve A	0.01	0.015	0.02	0.025	0.03	0.04	0.05	0.10	0.17	0.30
Dose toxicity curve 2	0.0001	0.01	0.05	0.1	0.12	0.3	1	1	1	1
Accuracy (percentage of trials)	0	0	2	5	27	58	9	0	0	0
Allocation (No. of patients)	1.1	1.4	2.4	4	8.9	12.6	5.1	0.5	0	0
Percentage of patients	3	4	7	11	25	35	14	1	0	0
Safety (No. of patients with DLTs)	0	0.02	0.13	0.42	1.1	3.8	5.1	0.5	0	0
Trial design 3
Initial curve A	0.01	0.015	0.02	0.025	0.03	0.04	0.05	0.10	0.17	0.30
Dose toxicity curve 3	0.05	0.1	0.12	0.3	0.5	0.6	0.7	0.8	0.9	0.99
Accuracy (percentage of trials)	1	5	25	40	23	5	0	0	0	0
Allocation (No. of patients)	2.6	4.2	7.5	8.7	7.1	3.5	1.7	0.5	0.1	0.009
Percentage of patients	7	12	21	24	20	10	5	1	0	0
Safety (No. of patients with DLTs)	0.1	0.5	0.9	2.6	3.5	2.1	1.2	0.4	0.1	0.009
Trial design 4
Initial curve B	0.06	0.125	0.19	0.25	0.31	0.37	0.44	0.50	0.56	0.63
Dose toxicity curve 2	0.0001	0.01	0.05	0.1	0.12	0.3	1	1	1	1
Accuracy (percentage of trials)	0	0	0	1	25	69	5	0	0	0
Allocation (No. of patients)	1.0	1.1	1.4	2.7	9.3	17.2	3.3	0	0	0
Percentage of patients	3	3	4	8	26	48	9	0	0	0
Safety (No. of patients with DLTs)	0	0.02	0.07	0.3	1.1	5.2	3.3	0	0	0

NOTE. No. of patients, 36; acceptable toxicity rate, 30%; assuming the model presented in O'Quigley et al¹ and presumed/initial curves used in Neuenschwander et al.²⁰ Bold font indicates the true MTD. Accuracy: percentage of trials of 1,000 simulated trials that selected each dose as the final MTD (eg, 56% of trials selected level 7 as the MTD in example 1).

Abbreviations: DLT, dose-limiting toxicity; MTD, maximum-tolerated dose.

In trial design 2 (Figure 1B), the initial presumed dose-toxicity relationship is assumed to be the same as that in Figure 1A. Let us assume that the true dose-toxicity curve for simulation purposes is steep. Hence, the true MTD will actually occur at dose level 6, and simulations predict that, on average, 12 to 13 patients will be treated at the MTD and five additional patients will be treated at the level above the MTD. If only a few DLTs are observed at the MTD (level 6 in this trial design), say two DLTs of eight patients (25%) at level 6 and, on average, we treat five additional patients at level 7, which is above the MTD, then all five will have a DLT. This example illustrates a scenario in which we expose a greater percentage of patients to treatment toxicity at levels above the MTD simply because the presumed initial dose toxicity could not anticipate the steepness of the true dose-toxicity curve for this drug.

In trial design 3 (Fig 1C), the presumed dose-toxicity curve is the same as in Figure 1A and 1B, favoring the last level. However, if the true dose-toxicity curve is steeper earlier, the MTD occurs at a lower dose level (level 4). Simulations show that, on average, about half of patients (3.5 of 7.1) will experience a DLT at the dose level above the MTD, which indicates an aggressive escalation scheme. The simulations show that on average, 40% of the trials will select the correct MTD, and 31% of the trials will select a dose that is too low (Table 1).

In trial design 4 (Fig 1D), the presumed (initial) dose-toxicity curve is selected so that it does not favor the last level as the MTD. Rather, it favors the middle dose range as the likely MTD (level 5). Figure 1D shows that even if the true dose-toxicity curve is steep (as it was in Fig 1B), then simulations show that no more than three to four patients will be overexposed above the MTD, a clinically acceptable outcome. Accuracy is also high (69% of trials selected the correct MTD; Table 1), so the operating characteristics of this trial indicate safe escalations and also lead to an accurate estimate of the MTD.

The accuracy of these designs is measured via the percentage of trials of 1,000 hypothetical trials that select the right MTD. Accuracy ranges from 40% to 70% (Table 1). Although an accuracy of 40% might seem low, this may be the best that can be achieved in a phase I design with a small sample size and limited or no pretrial information.⁶ Unless information is available from past studies (eg, historical data used to inform the presumed initial curve or other tuning parameters), a theoretical upper limit on accuracy exists.⁷ Designs with low accuracy should be avoided to ensure safety and efficiency. A substantial risk to the patient may exist in any human trial that is testing a drug with a potentially steep true dose-toxicity relationship (Figure 1B) that might not be predictable from animal studies. Hence, the operating characteristics of adaptive designs must always be incorporated into a protocol's statistical methodology section.

It may come as a surprise that the scenario in Figure 1B could happen 9% of the time. Additional design parameters such as updating the model more frequently so that de-escalation is recommended after a DLT or inserting an intermediate dose level when the true dose toxicity curve appears too steep based on initial treatment results can reduce this risk.⁸ Anticipating the location of the MTD is especially difficult in first-in-human trials, in which the preclinical safety data may not translate to human studies.⁹ It is recommended that first-in-human trials presume an initial dose-toxicity curve that assumes that each dose is equally likely to be the MTD (known as a “non informative prior” in Bayesian statistics) unless preclinical data or data from phase 0 studies or other evidence supports otherwise. A recent review of trials in oncology that have used model-based designs provides insights of when such an approach is reasonable.¹⁰ We also recommend performing thorough sensitivity analyses to investigate prior robustness.^11–13

One might conclude that having too many tuning parameters on which the operating characteristics are dependent is a drawback. However, tuning parameters allow the model to adapt more precisely to different clinical situations, provide flexibility to the investigators and, most importantly, protect patients. Many options exist, such as choosing to approach the MTD from a lower level, a conservative option known as “escalation with overdose control.”¹⁴ Alternatively, they may allow cohorts of patients to skip dose levels in an attempt to reach the MTD faster, if the dose-toxicity curve is assumed to be nearly flat.¹⁵ There are many clinical parameters that are important, such as the starting dose level,⁹ the DLT evaluation period, the types of adverse events that are considered DLTs per protocol,¹⁶ and how transparent the design is in terms of escalating, de-escalating, or maintaining the current level.

During formal scientific review, we have examined many studies that provide the design parameters but not the operating characteristics, which we know to be necessary to assess patient safety. In our experience, this deficiency often occurs in trials that use Bayesian model–based designs. A well-designed adaptive trial is dependent on the sensitivity of the operating characteristics, which are, in turn, dependent on specifying optimal design parameters. Caution must be exercised in the selection and evaluation of design parameters because of the underlying uncertainty inherent in predicting the MTD based on preclinical data or other single-agent trials when evaluating drug combinations. There is now an established class of adaptive designs with known performance,^1,4,17,18 and for these models, most of the information is published. When using such designs, it is sufficient to cite the published work as long as the trial is following the published design exactly. However, this is not true for trials that follow novel dose-escalation designs or designs that include adaptations to existing designs without published research evaluating their performance. This field is moving rapidly, with new designs customized for specific phase I trials that involve multiple drugs, complicated schedules, expansion cohorts, and enriched patient populations. In trials of drug combinations with information borrowed from single-agent trials and assumptions made for drug interactions, synergy and/or antagonism, investigators and reviewers need to be confident that the information borrowed or assumptions made are safe for patients. Overlapping toxicities, toxicity attribution, and dose-toxicity versus dose-efficacy effects in the setting of drug combinations are areas of active research.¹⁹ In Table 2, we suggest protocol assessment guidelines and a set of basic questions for investigators and reviewers to consider in assessing a design's performance. In the end, investigators and scientific reviewers must consider how both patient safety and the trial's objectives are met when a custom trial design is used.

Table 2.

Reviewing Phase I Protocols for Dose Escalation

Protocol Assessment Guidelines

1. Review all design parameters. Examples include but are not limited to:

Clinical parameters, such as starting dose, cohort size, DLT observation window, DLT definition, and safety stopping rules

Statistical parameters, such as initial curve (skeleton), model, prior distribution on model parameters, sample size, and safety stopping rules

If dose escalation is not driven by a model for some part of the trial, specify the rules that determine dose escalation, de-escalation, or trial termination.

2. Review the validity and generalizability of any historical data used in model updating.

Is the source of the historical data clear (reference, ongoing trial)?

Are the historical data relevant in this clinical setting?

Are assumptions clear regarding the role of the historical data? For example, if the MTD of single-agent trials informs the MTD of a combination regimen, have we established the MTD of the single agent?

Are the data heavily weighted (dominating) for this design, or will these data be overwritten after a specific number of patients has accrued?

3. Review the operating characteristics of the design over many hypothetical trials and scenarios to determine how robust they are to the tuning parameters. Operating characteristics should include but are not limited to:

Number of patients treated at each dose

Number of patients overdosed, underdosed, or treated at or close to the MTD

Number of trials selecting the true MTD over many (eg, 1,000) trials

How often does the trial terminate early because of safety stopping rules?

If the trial ends early, what is the MTD recommendation?

If the sample size is not fixed, report the average sample size and average trial duration.

4. Review the operating characteristics of the trial design based on model and design specifications as well as any escalation/de-escalation decisions made outside the model recommendations. This step evaluates the trial's final recommendation when ad hoc decisions overrule the model.

Abbreviations: DLT, dose-limiting toxicity; MTD, maximum-tolerated dose.

Glossary Terms

adaptive design models:

design models that allow adaptations to trial procedures of studies after their initiation without undermining the validity or integrity of the trials.

Bayesian statistics:

alternative statistical methods that incorporate prior knowledge into the probability calculations, adjusting for accumulated experience. Trials using Bayesian statistics can provide faster, more useful clinical trial information under certain circumstances than traditional statistical methods.

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

Disclosures provided by the authors are available with this article at www.jco.org.

AUTHOR CONTRIBUTIONS

Manuscript writing: All authors

Final approval of manuscript: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

Scientific Review of Phase I Protocols With Novel Dose-Escalation Designs: How Much Information Is Needed?

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or jco.ascopubs.org/site/ifc.

Alexia Iasonos

No relationship to disclose

Mithat Gönen

No relationship to disclose

George J. Bosl

No relationship to disclose