Electrochemical Na⁺ and Ca²⁺ gradients drive coupled-clock regulation of automaticity of isolated rabbit sinoatrial nodal pacemaker cells

We discovered how the coupling of Na⁺ and Ca²⁺ electrochemical gradients regulates cross talk of surface membrane and Ca²⁺ clocks to regulate automaticity via the coupled-clock system; our numerical model simulations detected “a window” of system parameters for this effect on normal automaticity that borders on abnormal automaticity.

Abstract

Coupling of an intracellular Ca²⁺ clock to surface membrane ion channels, i.e., a “membrane clock, ” via coupling of electrochemical Na⁺ and Ca²⁺ gradients (E_Na and E_Ca, respectively) has been theorized to regulate sinoatrial nodal cell (SANC) normal automaticity. To test this hypothesis, we measured responses of [Na⁺]_i, [Ca²⁺]_i, membrane potential, action potential cycle length (APCL), and rhythm in rabbit SANCs to Na⁺/K⁺ pump inhibition by the digitalis glycoside, digoxigenin (DG, 10–20 μmol/l). Initial small but significant increases in [Na⁺]_i and [Ca²⁺]_i and reductions in E_Na and E_Ca in response to DG led to a small reduction in maximum diastolic potential (MDP), significantly enhanced local diastolic Ca²⁺ releases (LCRs), and reduced the average APCL. As [Na⁺]_i and [Ca²⁺]_i continued to increase at longer times following DG exposure, further significant reductions in MDP, E_Na, and E_Ca occurred; LCRs became significantly reduced, and APCL became progressively and significantly prolonged. This was accompanied by increased APCL variability. We also employed a coupled-clock numerical model to simulate changes in E_Na and E_Ca simultaneously with ion currents not measured experimentally. Numerical modeling predicted that, as the E_Na and E_Ca monotonically reduced over time in response to DG, ion currents (I_CaL, I_CaT, I_f, I_Kr, and I_bNa) monotonically decreased. In parallel with the biphasic APCL, diastolic I_NCX manifested biphasic changes; initial I_NCX increase attributable to enhanced LCR ensemble Ca²⁺ signal was followed by I_NCX reduction as E_NCX (E_NCX = 3E_Na − 2E_Ca) decreased. Thus SANC automaticity is tightly regulated by E_Na, E_Ca, and E_NCX via a complex interplay of numerous key clock components that regulate SANC clock coupling.

NEW & NOTEWORTHY

We discovered how the coupling of Na⁺ and Ca²⁺ electrochemical gradients regulates cross talk of surface membrane and Ca²⁺ clocks to regulate automaticity via the coupled-clock system; our numerical model simulations detected “a window” of system parameters for this effect on normal automaticity that borders on abnormal automaticity.

the primary determinants of automaticity of sinoatrial nodal cells (SANCs) lie within mechanisms that regulate the slope of the spontaneous diastolic depolarization (DD). Although classical perspectives had posited SANC automaticity to be regulated exclusively by surface membrane ion channels, recent evidence indicates that a coupled-clock system operates within SANCs to regulate normal automaticity (52, 54). Specifically, the sarcoplasmic reticulum (SR), functioning as a Ca²⁺ clock, and the ensemble of sarcolemmal ion channels and transporters as a “membrane clock” (M clock), comprise a coupled system that ensures robust, but flexible, SANC function (16, 51). Because M clock component functions regulate [Ca²⁺]_i, the oscillatory substrate of the Ca²⁺ clock, the M clock indirectly regulates spontaneous local Ca²⁺ release (LCR), generated via ryanodine receptors of the Ca²⁺ clock. LCR activation of NCX is a crucial factor in clock coupling. Both the characteristics and rhythmicity of spontaneous LCRs beneath the SANC surface membrane during DD and the average action potential cycle length (APCL) and its variability (APCLV) inform on the fidelity of clock coupling within the system (19, 52, 54, 57). Thus the coupling of Na⁺ and Ca²⁺ electrochemical driving forces, V_m − E_Na and V_m − E_Ca, respectively, can be envisioned as the major regulator of the clock coupling that regulates SANC normal automaticity (16, 19, 25).

Although there have been numerous prior studies of changes of [Na⁺]_i, [Ca²⁺]_i, V_m, E_Na, and E_Ca effects on contraction and abnormal automaticity, evoked by digitalis glycosides (DG) in ventricular cells, and on both normal or abnormal automaticity in isolated SAN tissue (39, 41) and Purkinje fibers (11, 20, 21, 29–31, 35), how DG-induced changes in V_m, E_Na, and E_Ca regulate automaticity of individual SANCs remains unexplored.

We employed a high DG concentration (10–20 μmol/l) to effect Na⁺/K⁺ pump inhibition that would accelerate time-dependent increases in [Na⁺]_i and [Ca²⁺]_i and cause a reduction in maximum diastolic potential (MDP), leading to changes in E_Na and E_Ca (11) in a relatively short time (25 min), enabling comparison of changes in the experimentally measured parameters at varying times following DG exposure to a specific [Na⁺]_i at those specific times (11) and create a model simulation linked to a specific [Na⁺]_i increase. We measured membrane potential and spontaneous APCL, the APCL waveform, APCLV, [Na⁺]_i, the cytosolic Ca²⁺ transient induced by an action potential (AP), and LCR characteristics in subsets of single, isolated rabbit SANCs. Employing a coupled-clock SANC numerical model (26), we simulated, in silico, simultaneous effects of the experimentally measured increase in [Na⁺]_i over time, attributable to blockade of Na⁺/K⁺ ATPase by DG on MDP, E_Na, E_Ca, and E_NCX, spontaneous APCL, ion currents (I_f, I_NaK, I_CaL, I_CaT, I_bNa, I_NCX, and I_Kr), LCRs, SR Ca²⁺ pumping, systolic and diastolic cytosolic Ca²⁺ (Ca_cyt), and Ca²⁺ in the submembrane space (Ca_sub). This combined experimental and numerical modeling approach revealed how Na⁺ and Ca²⁺ electrochemical gradients in single, isolated SANCs regulate cross talk between surface membrane M and Ca²⁺ clock functions and their coupling to effect changes in SANC APCL.

MATERIALS AND METHODS

SANC isolation.

Spontaneously beating SANCs were isolated from male New Zealand white rabbits (Charles River Laboratories) weighing 1.8−2.5 kg, as previously described (47). Rabbits were deeply anesthetized in accordance with NIH guidelines for the care and use of animals, protocol no. 034LCS2016, which was approved by the NIH Animal Care and Use Committee. The heart was removed quickly and placed in the solution containing (in mmol/l): 130.0 NaCl, 24.0 NaHCO₃, 1.2 NaH₂PO₄, 1.0 MgCl₂, 1.8 CaCl₂, 4.0 KCl, and 5.6 glucose equilibrated with 95% O₂-5% CO₂ (pH 7.4 at 35.5°C). The sinoatrial node (SA) region was cut into small strips (∼1.0 mm wide) perpendicular to the crista terminalis (CT) and excised (47). The final SA node preparation consisted of SA node strips attached to the small portion of CT. The SA node preparation was washed twice in Ca²⁺-free solution containing (in mmol/l): 140.00 NaCl, 5.40 KCl, 0.50 MgCl₂, 0.33 NaH₂PO₄, 5.00 HEPES, and 5.50 glucose (pH = 6.9); the preparation was incubated at 35.5°C for 30 min in the same solution with addition of elastase type IIA (0.6 mg/ml; Sigma), collagenase type 2 (0.6 mg/ml; Worthington), and 0.1% bovine serum albumin (Sigma). The SA node preparation was washed in modified Kraftbruhe (KB) solution, containing (in mmol/l): 70.0 potassium glutamate, 30.0 KCl, 10.0 KH₂PO₄, 1.0 MgCl₂, 20.0 taurine, 10.0 glucose, 0.3 EGTA, and 10.0 HEPES (titrated to pH 7.4 with KOH); it was kept at 4°C for 1 h in KB solution containing 50 mg/ml polyvinylpyrrolidone (Sigma). Single cells were dispersed from the SA node preparation by gentle pipetting in the KB solution and stored at 4°C.

All experiments were performed at 35.5°C. Temperature was controlled by an Analog TC2BIP 2/3Ch Bipolar Temp controller from Cell MicroControls.

[Na⁺]_i measurements in intact single SANCs.

[Na⁺]_i was assessed by an IonOptix Myocam system (Ion-Optix) in spontaneously beating intact SANCs. [Na⁺]_i was measured with Na⁺-sensitive fluorescent dye benzofuran isophthalate (SBFI-AM; Molecular Probes) at 35.5°C. SANCs were loaded with 10 μmol/l of SBFI-AM and 10% Pluronic F-127 in Tyrode solution for 90–110 min at room temperature. Pluronic F-127 was used to facilitate loading. SANCs were washed in normal Tyrode solution for 20 min to ensure deesterification of the SBFI-AM to SBFI and placed in a temperature-controlled bath (at 35.5°C) on an inverted fluorescence microscope equipped with an LWD Fluor ×40 lens (Olympus). [Na⁺]_i was measured at baseline and every minute following DG (10 μmol/l) exposure by exposing spontaneously beating SANCs to the light, emitted by a 75-W mercury xenon lamp, passed through either a 340-nm or 380-nm band-pass filter (bandwidths were ± 15 nm) at 200 Hz. Emitted light was collected by a Hamamatsu photomultiplier tube. The ratio of fluorescence (340/380) represents the level of [Na⁺]_i. After each measurement of [Na⁺]_i, the F₃₄₀/F₃₈₀ ratios were calibrated (Fig. 1) using a dual-point approach (at 150 mmol/l and 0 mmol/l extracellular [Na⁺], [Na⁺]_o) in the presence of amphotericin (100 μmol/l) and monensin (100 μmol/l), as described previously (7, 10). Background fluorescence was corrected before the ratio was calculated. Autofluorescence was undetectable. The method provides a good fit to the data over the range of [Na⁺]_i studied.

Fig. 1.

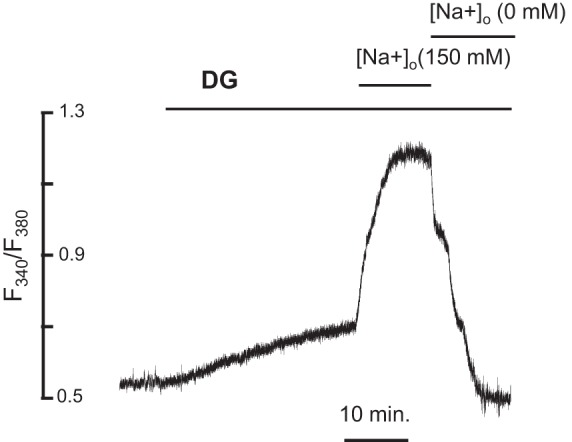
[Na⁺]_i measurements. Representative example of [Na⁺]_i measurement in a representative cell before and in the presence of digoxigenin (DG). F₃₄₀/F₃₈₀ was calibrated at the end of each experiment by sequentially applying solutions (see materials and methods) containing 150 mmol/l and 0 mmol/l extracellular sodium ([Na⁺]_o) in the presence of DG (10 μmol/l). Background fluorescence was corrected before the ratio was calculated. The short horizontal lines indicate the onset and the duration of the superfusion of the cells with calibration solutions containing 150 mM and 0 mM [Na⁺]_o in the presence of DG (10 μmol/l). The superfusion with normal Tyrode solution before calibration was 10 min.

Measurement of systolic and diastolic Ca²⁺ by Indo-1 in intact SANCs.

We measured time-dependent changes in systolic and diastolic [Ca²⁺]_i in response to DG via a calibrated ratiometric Ca²⁺ indicator, Indo-1, as described before (55). SANCs were placed in a chamber on an inverted fluorescence microscope stage (Zeiss IM-35), were loaded with 14 μmol/l Indo-1 AM (Molecular Probes) for 15 min at room temperature, and were subsequently superfused with Tyrode solution for 20 min to remove excess indicator. To allow full deesterification, the bath temperature was slowly increased to 35.5°C. The apparatus to detect Indo-1 fluorescence was described previously (38) except that a ×63/1.4 N.A. oil UV fluorglycerin-immersion objective (Zeiss) was used. Indo-1 fluorescence was corrected for background, and autofluorescence was determined in every experiment by subtracting averaged signals from cells not loaded with Indo-1 (n = 5). [Ca²⁺]_i was calculated as previously described (55).

AP recordings and AP waveform analysis in single intact SANCs.

Spontaneous APs were recorded by a perforated patch-clamp technique with 0.05 mmol/l of β-escin added to the electrode solution that contained (in mmol/l): 120 K-gluconate, 5 NaCl, 3 Mg-ATP, 5 HEPES, 20 KCl, 3 Na₂ATP (pH adjusted to 7.2 with KOH) (47). SANCs were continuously superfused with normal Tyrode solution containing (in mmol/l): 140.0 NaCl, 5.4 KCl, 5.0 HEPES, 2.0 MgCl₂, 1.8 CaCl₂, and 10.0 glucose (pH 7.4). APs were recorded by a standard zero-current-clamp technique (Axopatch 200B; Molecular Devices). Experiments were terminated following ∼25 min of DG exposure.

The APCL and AP characteristics were analyzed via a customized program (4, 24). The APCL was measured either as the interval between AP upstrokes (maximum dV/dt, V/s), or, in a subset of cells, as the interval between AP-induced Ca²⁺ transient. Other measured AP parameters also include MDP, AP overshoot (MaxV), AP amplitude, AP upstroke (dV/dt_max), AP duration measured at 90% of repolarization time (APD₉₀), time from MDP to the onset of nonlinear DD (TNLDD), and time from previous maximum AP to MDP (tMDP). Beat-to-beat variations (percent change) in spontaneous APCLs and other selected AP parameters were assessed in each cell by the coefficient of variation (CV), calculated as standard deviation divided by its mean (CV = SD/mean·100).

The average [Na⁺]_i was assigned to each cell as its [Na⁺]_i at a specific time point during continuous AP recordings when APCL reached reference points following DG exposure (short APCL, back-to-base APCL, above-base APCL, and grossly dysrhythmic APCL).

Local Ca²⁺ signal imaging in single intact SANCs.

Ca²⁺ transients and spontaneous diastolic LCRs were recorded in intact SANCs superfused with the normal Tyrode solution (see above) at baseline and in the presence of DG (10–20 μmol/l) by confocal microscopy (Zeiss LSM-410 inverted confocal microscope; Carl Zeiss). We used a 488-nm argon ion laser for excitation of fluo-4 AM (10 μmol/l), and the fluorescence signal was collected at wavelengths of >515 nm in line-scan mode oriented along the cell periphery (46).

Local Ca²⁺ signal imaging in permeabilized SANCs.

To determine whether DG directly affects the SR Ca²⁺ cycling, we measured LCRs in permeabilized (with saponin, 0.01%) SANCs at 100 nmol/l [Ca²⁺]_i, as previously described (36). LCRs were measured by confocal microscopy in the recording solution containing (in mmol/l): 100.00 DL-aspartic acid potassium salt, 25.00 KCl, 10.00 NaCl, 3.00 MgATP, 0.81 MgCl₂, 20.00 Hepes, 0.50 EGTA, 10.00 phosphocreatine; this was in addition to 5.00 U/ml creatine phosphokinase (pH 7.2 adjusted with KOH). Fluo-4 salt (30 μmol/l) and Ca²⁺ were added to the recording solutions. The final free [Ca²⁺]_i = 100 nmol/l was calculated by a computer program (WinMAXC 2.50, Stanford University).

Analysis of diastolic local Ca²⁺ signals.

Fluo-4 measurements of LCRs in intact SANCs are presented as F/F₀ (normalized Ca²⁺ signal). LCR spatial size was indexed as the full width at the half-maximum amplitude (FWHM), and its duration was characterized as the full duration at half maximum amplitude (FDHM). LCR events were normalized per 100 μm of the line-scan image and during a 1-s time interval (36). The Ca²⁺ signal of an individual LCR was estimated as follows: LCR = FWHM × FDHM(F/F₀ − 1)/2. The Ca²⁺ signal of the LCR ensemble within a cell was calculated as the sum of all Ca²⁺ signals of individual LCRs (36). All images were processed with IDL software (6.1., Research Systems).

In silico numerical modeling of DG effects.

A coupled-clock model of rabbit SANCs (26) was employed to explore various responses to the experimentally measured time-dependent increase in [Na⁺]_i during blockade of Na⁺/K⁺ ATPase current. In these simulations, we assumed that, in the presence of DG, the remaining Na⁺/K⁺ ATPase activity (and I_NaK density) is 30% of baseline (before drug application), as previously reported (49). The time-dependent increase in [Na⁺]_i was simulated by clamping [Na⁺]_i using a slow ramp (0.075 mmol/l per s) from 8 mmol/l to 14 mmol/l and simultaneously simulating at a given [Na⁺]_i dynamic changes in V_m, I_NCX, I_f, I_CaL, I_CaT, I_Kr, I_NaK, I_bNa, LCRs, Ca_sub (submembrane Ca²⁺), Ca_cyt (cytosolic Ca²⁺), and diastolic SR Ca²⁺ release flux (j_Carel).

Experimental design.

The increase in [Na⁺]_i and other variables was monitored over time following exposure to a high concentration of DG (10–20 μmol/l), to effect a wide-range [Na⁺]_i increase within a relatively brief period of time, about 25 min. The high concentration of DG (20 μmol/l) has been used in a similar experimental approach in ventricular myocytes (1). In our study, we tested DG-induced effects on spontaneous APCL and the APCL waveform, [Na⁺]_i, the systolic and diastolic [Ca²⁺], and spontaneous LCR in subsets of single, isolated rabbit SANCs via different techniques (patch clamp, confocal microscopy, Indo-1, and IonOptix Myocam system). The time of ∼25 min was chosen based on the time window of the most reliable AP recording. Specifically, during continuous AP recordings, each perforated patch-clamp experiment has three phases: phase 1, when GigaOhm seal is established and β-escin is perforating the membrane patch (within about 4–5 min) to allow electrical access into the cell; phase 2, when perforation is completed and AP can be reliably measured; phase 3, when AP recording becomes unstable as the GigaOhm seal starts to deteriorate after 25–30 min in spontaneously beating SANCs. To have comparable measurements between different experiments, we used ∼25–30 min as an end point for the experiment.

Drugs.

DG (C₂₃H₃₄O₅) was obtained from Sigma.

Statistics.

Data are presented as means ± SE (n = number of SANCs). P < 0.05 is considered statistically significant. A linear mixed-effects model with a Dunnett's post hoc adjustment to the P value to compare each time point with the baseline was used to test changes of AP-induced Ca²⁺ transients and systolic and diastolic [Ca²⁺]_i measured by Indo-1 in response to DG. A linear mixed-random effects model for repeated measures (44) followed by Bonferroni adjustment of the P values for multiple comparisons were used to test changes of AP waveform and local Ca²⁺ signals in response to DG, measured by patch clamp and confocal microscopy, respectively. The two-sample paired t-test for means was used to compare [Na⁺]_i before and after DG exposure in intact single SANCs.

RESULTS

DG-induced changes in [Na⁺]_i.

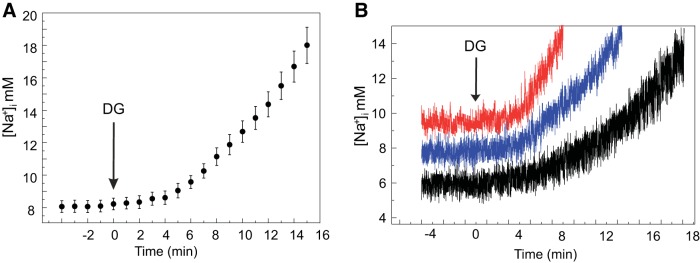
Changes in [Na⁺]_i measured in a subset of SANCs (n = 7), at baseline and every minute following 10 μmol/l DG exposure, are presented in Fig. 2. By employing a high DG concentration to effect an increase in [Na⁺]_i in a relatively short time (20–25 min), we could relate changes in the experimentally measured parameters at varying times following DG exposure to a specific [Na⁺]_i at those times (11) and create model simulations linked to a specific [Na⁺]_i increase. The average [Na⁺]_i increased exponentially over the time following DG exposure (P < 0.05) (Fig. 2A). Note that the rate at which [Na⁺]_i increased over time following DG exposure varied among cells (Fig. 2B).

Fig. 2.

[Na⁺]_i increases in response to DG in spontaneously beating sinoatrial nodal cells (SANCs). A: average [Na⁺]_i change at baseline and every minute following 10 μmol/l DG exposure in spontaneously beating SANCs (n = 7). The arrow indicates the time when superfusion with DG started (2-sample paired t-test for means was used to compare [Na⁺]_i before and after DG exposure; see details in Table 2). B: example of [Na⁺]_i change in 3 different SANCs.

Effect of DG on spontaneous APCL and MDP.

Figure 3 illustrates a continuous recording of time-dependent effects of DG on the spontaneous APCL (Fig. 3A, arrow indicates the onset of DG exposure) and MDP (Fig. 3B) in the SANC. Examples of the AP waveform in this cell at baseline (before DG) and at varying times following DG administration are illustrated in Fig. 4.

Fig. 3.

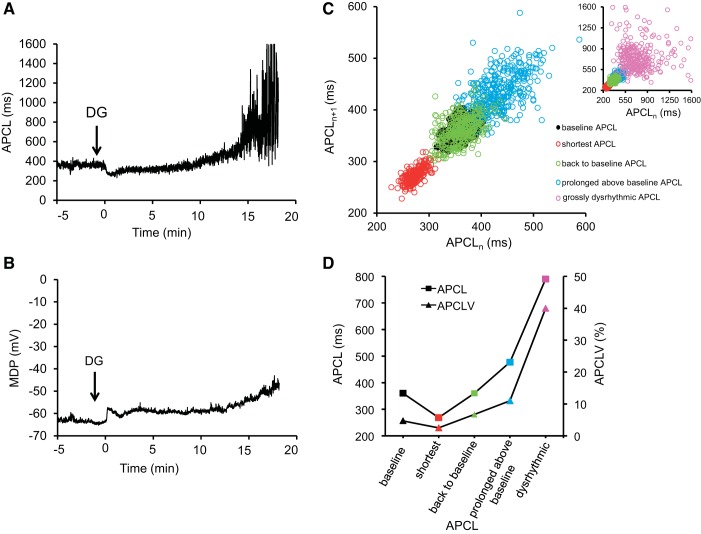
Time-dependent effect of DG on spontaneous action potential cycle length (APCL) and maximum diastolic potential (MDP) in a single SANC. A and B: examples of continuous recordings of time-dependent effects of DG (10 μmol/l) on the spontaneous APCL and MDP. The arrow indicates the time when superfusion with DG started. C: Poincaré plots, which display each APCL as a function of preceding APCL at baseline and at selected times (at shortest APCL, back to baseline APCL, prolonged above baseline APCL, grossly dysrhythmic APCL) following DG exposure in the same cell presented in A. D: comparison of the average beat-to-beat variation of APCL and the average coefficient of variation of APCL (APCLV) of the same cell in A at baseline and during DG exposure at the same times as in C.

Fig. 4.

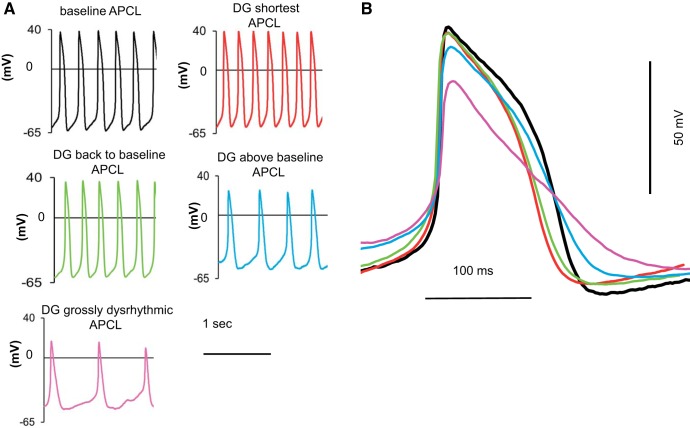
Alterations in the action potential (AP) waveform in response to DG. A: representative examples of AP recordings at baseline and at selected times (at minimum APCL, APCL prolongation back to baseline, APCL prolongation above baseline, and grossly dysrhythmic APCL) following DG (10 μmol/l) exposure in the same cell. B: overlay of the AP waveforms (synchronized at the AP overshoot) at baseline and during DG response in the same cell presented in A (colors in B match colors in A).

The earliest response to DG was a reduction in APCL (Fig. 3A). The time to achieve the minimum APCL following DG exposure varied among cells (Table 2). On average, APCL decreased to 61.7 ms (18%) from 349.9 ± 14.8 ms at baseline to 288.2 ± 11.1 (P < 0.05, Table 1) and was accompanied by a small (5%) but significant increase in [Na⁺]_i, from 8.4 ± 0.4 mmol/l at baseline to 8.9 ± 0.1 mmol/l at the shortest APCL (P < 0.05, Table 2). At the time at which the APCL reached its nadir in each cell, MDP was reduced (Fig. 3). On average, MDP was reduced from −58.2 ± 1.4 mV at baseline to −55.0 ± 2.0 mV at the time when average APCL reached its nadir (Table 1).

Table 2.

Changes of APCL and [Na⁺]_i in the individual SANCs in response to DG

Cell No.	Baseline APCL, ms	Short APCL, ms	[Na+]i, mM	DG Time, min	Back to Baseline APCL, ms	[Na+]i, mM	DG Time, min	Above Baseline APCL, ms	[Na+]i, mM	DG Time, min	Grossly Dysrhythmic APCL, ms	[Na+]i, mM	DG Time, min
1	361.0	268.3	8.7	2.0	360.0	13.1	10.0	413.0	18.2	17.0	782.1	18.2	21.0
2	278.7	214.9	8.7	2.0	278.0	13.1	10.0	346.4	18.2	15.0	801.4	18.2	19.0
3	305.4	281.3	8.7	2.0	305.0	9.6	5.0	328.9	11.5	7.5
4	348.3	285.6	8.7	2.0	347.5	13.1	10.0	400.0	18.2	13.5	630.1	18.2	16.5
5	334.9	313.9	9.3	4.0	334.9	15.3	12.0	379.4	18.2	14.0
6	407.3	330.7	8.7	2.0	406.1	10.1	6.0	472.8	11.5	8.0	485.9	13.8	11.0
7	367.1	333.9	8.9	3.0	367.6	10.1	6.0	451.0	13.1	14.0	751.3	16.6	17.0
8	423.0							562.1	9.6	5.0	596.4	11.5	8.0
9	434.1	303.7	8.7	1.8
10	339.6							426.0	13.1	10.0	741.4	18.2	15.0
11	313.2	282.7	8.7	2.0
12	286.5	266.8	9.6	4.5	286.0	11.5	7.5
	349.9 ± 14.8	288.1 ± 11.1*	8.9 ± 0.1§	2.5 ± 0.3	335.6 ± 15.5†	12.0 ± 0.7§	8.3 ± 0.9	420.0 ± 23.5*†‡	14.6 ± 1.2†	11.6 ± 1.4	684.1 ± 43.9	16.4 ± 1.0	15.4 ± 1.7

Applicable values are means ± SE. [Na⁺]_i was assigned to each cell from the average [Na⁺]_i curve (Fig. 2) at the time point when each cell APCL reached reference points following DG exposure (short APCL, back to base APCL, above base APCL, grossly dysrhythmic APCL). The 2-sample paired t-test for means was used to compare [Na⁺]_i before and after DG exposure.

^*P < 0.05 vs. baseline;

^†P < 0.05 vs. short;

^‡P < 0.05 vs. back to baseline via a linear mixed-random effects model to analyze APCL repeated measurements (with Bonferroni adjustments for P values);

^§P < 0.05 vs. baseline [Na⁺]_i = 8.4 ± 0.4 mM. APCLs recorded during grossly dysrhythmic APCLs were excluded from statistical comparison (see details in Table 1).

Table 1.

AP waveform parameters in intact SANCs at baseline and during DG exposure

	Baseline (n = 12)	Short (n = 10)b	Back to Baseline (n = 8)c	Prolonged Above Baseline (n = 9)d	Grossly Dysrhythmica (n = 7)e
After DG, min	0	2.5 ± 0.3	8.3 ± 0.9	11.6 ± 1.4	15.4 ± 1.7
APCL, ms	349.9 ± 14.8	288.2 ± 11.1*	335.6 ± 15.5†	420.0 ± 24.0*†‡	684.0 ± 43.9
MaxV, mV	35.2 ± 2.1	32.8 ± 2.3	32.0 ± 3.0	26.3 ± 3.1*	23.5 ± 3.7
MDP, mV	−58.2 ± 1.4	−55.0 ± 2.0	−54.4 ± 2.7	−47.8 ± 2.8*†‡	−49.8.0 ± 1.0
Amplitude, mV	93.6 ± 2.7	87.8 ± 2.3	86.7 ± 4.1	74.1 ± 5.3*†‡	73.3 ± 3.3
dV/dtmax, V/s	10.3 ± 1.2	8.8 ± 0.8	8.7 ± 1.0	5.7 ± 1.2*	4.8 ± 1.1
APD90, ms	185.9 ± 9.1	150.7 ± 6.0*	166.4 ± 7.3†	212.5 ± 13.2†‡	374.4 ± 17.4
TNLDD, ms	184.7 ± 15.0	132.2 ± 7.8*	176.8 ± 12.4†	252.8 ± 24.0*†‡	546.3 ± 68.7
tMDP, ms	150.2 ± 10.0	134.6 ± 7.8	139.5 ± 7.4	150.5 ± 7.8	182.8 ± 13.4

Values are means ± SE.

^*P < 0.05 vs. baseline;

^†P < 0.05 vs. short;

^‡P < 0.05 vs. back to baseline.

Only relatively stable action potential (AP) cycle lengths (APCLs) were used for statistical comparison by a linear mixed-effects model to analyze repeated measurements (Bonferroni adjustment was made to the P values).

^aParameters recorded during grossly dysrhythmic APCLs were excluded from statistical comparison.

^bThis pattern of average APCL reduction in response to digoxigenin (DG) was observed in 10 out of 12 sinoatrial nodal cells (SANCs). Two other SANCs showed only a prolongation of APCL above baseline during the experiment.

^cTwo of 10 SANCs in which APCL was initially reduced failed to achieve the pre-DG baseline, and their average APCL remained shorter than the original pre-DG baseline value during the remaining experiment.

^dNine SANCs exhibited this behavior, 7 of 8 SANCs that previously had returned to pre-DG baseline and the 2 SANCs that exhibited only APCL prolongation during the experiment. One from 8 SANCs that reached the pre-DG baseline value failed to prolong above baseline during the remaining experimental time.

^eThese marked grossly dysrhythmic APCLs were registered in 7 from 9 SANCs in which APCL was originally prolonged at earliest of DG response. In 2 other SANCs, APCL was prolonged but remained relatively rhythmic.

MDP, maximum diastolic potential; APD₉₀, AP duration measured at 90% of repolarization time; TNLDD, time from MDP to the onset of nonlinear diastolic depolarization.

Achievement of the shortest APCL in a given cell was followed by gradual prolongation of APCL toward the original baseline in that cell (Fig. 3B). The time to return to the pre-DG baseline APCL varied among SANCs in which APCL initially became reduced in response to DG and was, on average, 8.3 ± 0.6 min after DG exposure (Table 2). At this time, when the original pre-DG average APCL was achieved, the average [Na⁺]_i increased to 12.0 ± 0.7 mmol/l (Table 2), and the average MDP was −54.4 ± 2.7 mV (Table 1).

Following achievement of the pre-DG APCL baseline, APCL continued to prolong, and MDP became further reduced (Fig. 3, A and B). The average APCL increased by 70 ms above baseline (P < 0.05, Table 1), and average MDP decreased from −58.2 ± 1.4 mV at baseline to 47.8 ± 2.8 mV (P < 0.05, Table 1). At this time, the average [Na⁺]_i increased to 14.6 ± 1.2 mmol/l (Table 2). The time to achieve this response to DG varied among SANCs; on average it was 11.6 ± 1.4 min (Table 2). Although there was significant prolongation in APCL (P < 0.05), gross arrhythmias were still not observed during this stage of the DG response.

As the time following DG exposure increased, the stage of prolonged but still relatively stable APCLs was followed by marked MDP depolarization and by gross prolongation of APCL (Figs. 3 and 4). On average, the time to reach this stage of the DG response varied among SANCs and was 15.4 ± 1.7 min (Table 2), and the average APCL at this stage became prolonged to 334.2 ms above baseline (P < 0.05, Table 1), the average MDP decreased further to 49.6 ± 1.1 mV (P < 0.05, Table 1), and the average [Na⁺]_i increased to 15.4 ± 1.7 mmol/l.

AP waveform parameters.

In addition to APCL and MDP, other measured parameters of the AP waveform in response to DG varied over time (Table 1). Figure 4 illustrates the AP waveform of the cell presented in Fig. 3. When APCL achieved the pre-DG baseline level, the AP amplitude began to decrease (Fig. 4, green traces) and continued to decrease further (Fig. 4, blue and pink traces) as the time of DG exposure increased (Table 2). On average, the AP amplitude among cells was significantly reduced from 93.6 ± 2.7 mV at baseline to 74.1 ± 5.3 mV (P < 0.05, Table 1) as the time of DG exposure increased, on average, to 11.6 ± 1.4 min. Note that the biphasic change in APCL as the time in DG increased is paralleled by biphasic changes in the TNLDD and APD₉₀ (Table 1). In contrast, the MDP, AP amplitude, AP upstroke (dV/dt_max), and AP overshoot (MaxV) monotonically decreased over time in response to DG. Thus the effects of DG on SANC automaticity included an initial reduction in APCL, MDP, and other AP waveform characteristics including TNLDD (Table 1). This phase was followed by gradual prolongation of APCL, TNLDD, APD₉₀, and a progressive reduction of MDP, AP amplitude, MaxV, and dV/dt_max; grossly dysrhythmic APCL evolved in 7 out of 12 cells (Tables 1 and 2). These time-dependent effects of DG on APCL and MDP occurred commensurately with graded, time-dependent increases in [Na⁺]_i (Fig. 2). Of note, there was substantial heterogeneity in the times to achieve hallmarks of the various stages of [Na⁺]_i, [Ca²⁺]_i, and APCL in response to DG.

APCLV in response to DG.

APCLV was calculated as a beat-to-beat variation in spontaneous APCLs during continuous AP recordings and reported as CV (%). Variability in the APCL, which informs on SANC clock coupling (52, 57), emerged during exposure to DG, even before the advent of grossly dysrhythmic APCL. The APCLV slightly decreased as APCL decreased in the cell in Fig. 3 during the early response to DG and then increased when APCL prolonged back to baseline and above baseline values with longer time of DG exposure (Fig. 3D). In the cell in Fig. 3, cycle-to-cycle APCLV at baseline and during exposure to DG are also revealed in a Poincaré plot (Fig. 3C). Specifically, in the Poincaré plot, in which each AP beating interval (APCL) is plotted against its predecessor, the scattering between two successive APCLs reflects the response to DG. Poincaré plots of the cell described in Fig. 3A revealed four different stages of changes over time following DG exposure; when the APCL became reduced following DG exposure, the dispersion among APCLs decreased (red markers in Fig. 3C); then, as the APCL prolonged back to pre-DG baseline, dispersion among APCLs then slightly increased (green markers in Fig. 3C) vs. baseline (black markers in Fig. 3C); as the APCL became prolonged above baseline as time to DG exposure increased, APCLV increased further (blue markers in Fig. 3C); when the APCL became grossly dysrhythmic, the dispersion of subsequent APCLs increased dramatically (pink markers in Fig. 3C, inset). The average APCLV among cells along with CV of other AP parameters at baseline and during the reference points following DG exposure, noted above, are listed in Table 3.

Table 3.

CV of AP waveform parameters

	Baseline (n = 12)	Short (n = 10)b	Back to Baseline (n = 8)c	Prolonged Above Baseline (n = 9)d	Grossly Dysrhythmica (n = 7)e
After DG, min	0	2.5 ± 0.3	8.3 ± 0.9	11.6 ± 1.4	15.4 ± 1.7
APCL, %	3.5 ± 0.3	3.1 ± 0.3	5.1 ± 1.4	8.8.1 ± 1.5*†‡	29.2 ± 2.9*
MaxV, %	2.1 ± 0.4	2.7 ± 0.5	5.6 ± 3.2	10.5 ± 3.0*†	37.4 ± 12.5*
MDP, %	1.0 ± 0.1	1.7 ± 0.5	1.7 ± 0.5	3.8 ± 1.8*	4.0 ± 0.7*
Amplitude, %	1.2 ± 0.2	1.9 ± 0.4	2.5 ± 1.3	5.4 ± 1.7*	10.3 ± 2.3*
dV/dtmax, %	4.8 ± 0.7	5.7 ± 1.0	7.0 ± 3.0	11.9 ± 2.5*	29.5 ± 6.1*
APD90, %	5.2 ± 0.7	3.8 ± 0.4	4.8 ± 0.8	14.9 ± 4.1*†‡	72.3 ± 11.1*
TNLDD, %	8.6 ± 0.7	10.3 ± 1.6	11.9 ± 2.0	33.8 ± 8.0*†‡	133.3 ± 21.8*
tMDP, %	4.0 ± 0.2	4.5 ± 0.2	4.6 ± 0.4	7.4 ± 0.7*†‡	39.5 ± 16.5*

Values are means ± SE. Coefficients of beat-to-beat variation (CVs, percent of change) of AP waveform parameters were compared by a linear mixed-random effects model for repeated measures with Bonferroni adjustment of the P values.

^*P < 0.05 vs. baseline;

^†P < 0.05 vs. short;

^‡P < 0.05 vs. back to base.

^aCVs during grossly dysrhythmic APCLs were compared by paired t-test vs. baseline only.

^bThis pattern of average APCL reduction in response to DG was observed in 10 out of 12 SANCs. Two other SANCs showed only a prolongation of APCL above baseline during the experiment.

^cTwo of 10 SANCs in which APCL was initially reduced failed to achieve the pre-DG baseline, and their average APCL remained shorter than the original pre-DG baseline value during the remaining experiment.

^dNine SANCs exhibited this behavior, 7 of 8 SANCs that previously had returned to pre-DG baseline and the 2 SANCs that exhibited only APCL prolongation during the experiment. One from 8 SANCs that reached the pre-DG baseline value failed to prolong above baseline during the remaining experimental time.

^eThese marked grossly dysrhythmic APCLs were registered in 7 from 9 SANCs in which APCL was originally prolonged at earliest of DG response. In 2 other SANCs, APCL was prolonged but remained relatively rhythmic.

Strikingly noticeable is that, when the APCL became prolonged at an averaged time of 11.6 ± 1.4 min (Table 2), the CVs of all AP parameters were all significantly increased above baseline values (Table 3), even though APCLs at that point still were not grossly dysrhythmic (Figs. 3 and 4, blue plots).

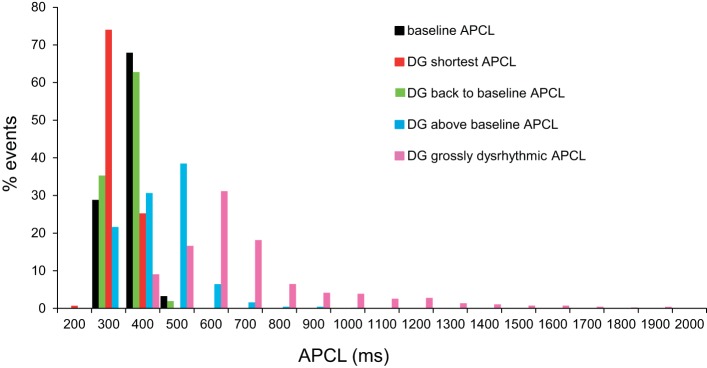
Histogram distributions of all individual APCLs in all cells in response to DG are illustrated in Fig. 5. Note that the histogram distribution of APCLs (Fig. 5) shifts to the left of baseline when the average APCL is reduced; the distribution shifts back to baseline when the average pre-DG APCL is achieved; then, at longer times following DG exposure, the distribution of APCLs becomes skewed far off to the right, even in the absence of grossly dysrhythmic APCL; this distribution becomes very broad when grossly dysrhythmic APCLs occur.

Fig. 5.

Distributions of spontaneous APCLs over the time course of the DG response. Distribution of individual spontaneous APCLs, measured during continuous APCL recordings at baseline and at times as in Fig. 4 following DG (10 μmol/l) exposure (at shortest APCL, APCL prolongation back to baseline, APCL prolongation above baseline, and grossly dysrhythmic APCL) (n = 13,363 APCLs).

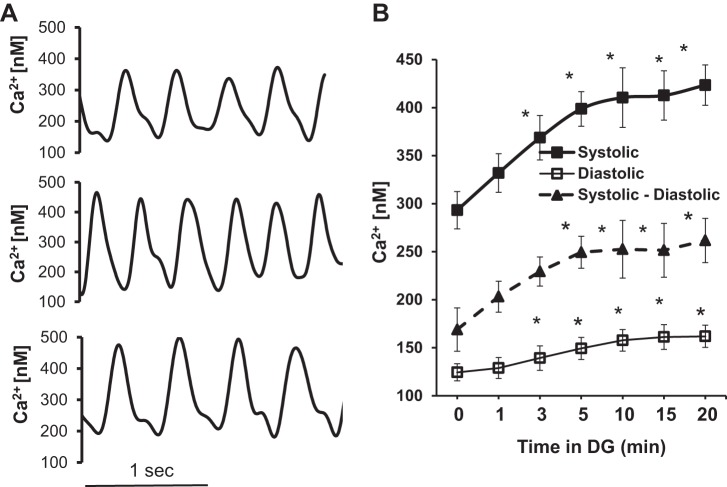
Diastolic Ca²⁺ and systolic Ca²⁺ transients.

Diastolic [Ca²⁺]_i and peak [Ca²⁺]_i and the AP-induced Ca²⁺ transient (peak [Ca²⁺]_i-diastolic [Ca²⁺]_i) were measured with the ratiometric Ca²⁺ indicator, Indo-1 AM. Figure 6A shows Indo-1 AM recordings in single SANCs at baseline (Fig. 6A, top) and during DG exposure (Fig. 6A, middle and bottom). Average data for diastolic and peak [Ca²⁺]_i and their differences (the Ca²⁺ transient) measured at baseline and at 5-min intervals following DG exposure are illustrated in Fig. 6B and listed, along with other parameters of Ca²⁺ transient, in Table 4. The average diastolic [Ca²⁺]_i, AP-induced peak [Ca²⁺]_i, and Ca²⁺ transient amplitude (peak-diastolic) increased as a function of time following exposure to DG. The rates at which these increases occurred following exposure to DG varied among cells, similar to the time-dependent increase in [Na⁺]_i. The time controls for the data in Table 4 did not significantly change (Table 5).

Fig. 6.

Spontaneous AP-induced Ca²⁺ transients, systolic and diastolic [Ca²⁺]_i measured by Indo-1 in spontaneously beating SANCs in the presence of DG. A: representative examples of AP-induced Ca²⁺ transients recorded in normal Tyrode solution by Indo-1 at baseline (top), and at 3 and 10 min following DG exposure (middle and bottom, respectively). B: average changes in the amplitude of systolic, diastolic [Ca²⁺]_i, and AP-induced Ca²⁺ transient at baseline and during a 20-min superfusion with 10 μmol/l DG (P < 0.05 vs. baseline via a linear mixed-effects model with a Dunnett's post hoc test for the P values; n = 5).

Table 4.

Average characteristics of spontaneous AP-induced Ca²⁺ transients, systolic and diastolic [Ca²⁺]_i measured by Indo-1 in the presence of DG (10 μmol/l)

Time in DG, min	0	1	3	5	10	15	20
Systolic Ca2+, nM	293.2 ± 19.4	331.9 ± 20.1	368.6 ± 23.2*	398.6 ± 18.0*	410.4 ± 31.0*	412.6 ± 25.6*	423.4 ± 21.0*
Diastolic Ca2+, nM	124.3 ± 8.9	128.8 ± 10.9	139.2 ± 12.7*	149.2 ± 11.5*	157.7 ± 11.2*	161.1 ± 12.9*	161.8 ± 11.6*
Ca2+ transient, nM	168.9 ± 22.6	203.1 ± 16.1	229.3 ± 15.2	249.4 ± 16.7*	252.5 ± 30.1*	251.5 ± 28.0*	261.6 ± 23.0*
T-Pc, ms	116.1 ± 9.4	98.3 ± 5.1	109.1 ± 3.8	107.2 ± 9.9	111.3 ± 5.3	110.5 ± 6.8	136 ± 18.6
T-90c, ms	287.2 ± 16.1	262.6 ± 25.7	295.4 ± 18.1	301.7 ± 19.6	320.5 ± 13.4	333.0 ± 16.5*	365.2 ± 19.1*

Values are means ± SE. A linear mixed-effects model with a Dunnett's post hoc adjustment to the P value was used to compare each time point in DG with the baseline (0 min). T-P_c, time to peak; T-90_c, time to decay.

^*P < 0.05 vs. baseline (n = 5).

Table 5.

Average characteristics of spontaneous AP-induced Ca²⁺ transients, systolic and diastolic [Ca²⁺]_i measured by Indo-1 in time control cells in the absence of DG

Time, min	0	1	3	5	10	15	20
Systolic Ca2+, nM	311.5 ± 26.2	317.2 ± 23.6	323.9 ± 38.1	331.5 ± 24.7	324.0 ± 30.7	334.0 ± 27.7	331.2 ± 28.1
Diastolic Ca2+, nM	126.2 ± 8.0	126.7 ± 7.1	126.6 ± 5.8	127.3 ± 7.4	130.0 ± 7.6	131.3 ± 8.8	135.3 ± 8.3
Ca2+ transient, nM	197.2 ± 13.3	209.6 ± 16.6	202.3 ± 18.3	196.2 ± 16.6	200.0 ± 15.1	207.8 ± 16.2	204.5 ± 15.0
T-Pc, ms	107 ± 7.9	105 ± 10.4	106.9 ± 5.2	100.9 ± 4.2	108.2 ± 2.8	107.6 ± 8.0	114.4 ± 6.4
T-90c, ms	291.8 ± 18.4	291.5 ± 21.9	316.3 ± 24.1	292.2 ± 28.6	302.3 ± 20.3	317.8 ± 23.1	281.5 ± 22.5

Values are means ± SE. Time controls were recorded in different cells (n = 5), P > 0.05.

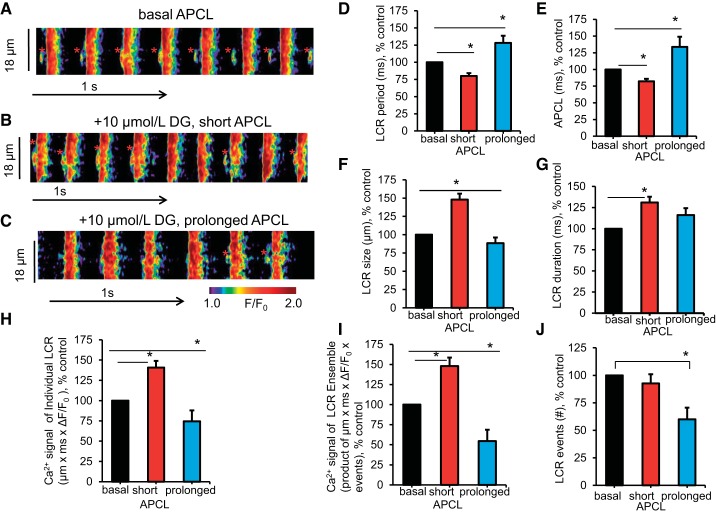
Confocal imaging of spontaneous local diastolic ryanodine receptor (RyR) activation was measured as LCRs in SANCs with intact sarcolemmal function. Figure 7, left, illustrates representative examples of confocal line-scan images of SANCs loaded with the Ca²⁺-sensitive fluorescent dye fluo-4 AM at baseline and at different times following DG exposure. Note that, unlike the APCL, which can be recorded continuously during DG exposure, recordings of fluo-4 fluorescence cannot be continuous because of bleaching of the probe. In other words, short recording of LCRs (asterisks in Fig. 7, A–C) and AP-induced Ca²⁺ transients were necessary. The times at which we recorded LCRs and AP-induced Ca²⁺ transients were guided by the average times to achieve reference points following DG exposure during continuous AP recordings (Table 2).

Fig. 7.

Effect of DG on spontaneous local diastolic Ca²⁺ releases (LCRs) in intact, spontaneously beating SANCs. A–C: representative examples of confocal line-scan images of SANCs loaded with the Ca²⁺-sensitive fluorescent dye fluo-4 AM (10 μmol/l) in the same cell at baseline and in response to DG (10 μmol/l) at 2 min (B) and 8 min (C). LCRs are marked with asterisks. D and E: the average change (% of baseline) of AP-induced Ca²⁺ transient cycle length, a faithful proxy of the APCL, and LCR period at baseline and at time points shown in A of DG (10–20 μmol/l) response. F–J: average change (% of baseline) of LCR characteristics at baseline (n = 16 SANCs) and at time points shown in A of DG response (in 7 of 16 SANCs, both reduction and prolongation of APCL were recorded in response to DG; 6 of 16 SANCs exhibited only reduced APCL; 3 of 16 SANCs showed only prolonged APCL in response to DG during the experimental time; *P < 0.05 via linear mixed-effects model for repeated measurements with Bonferroni adjustment for the P values).

Figure 7, right, illustrates the average change in the spontaneous AP-induced Ca²⁺ transient cycle length, the faithful proxy of the APCL (57), LCR period, and other LCR characteristics, measured in SANCs loaded with the Ca²⁺ indicator, fluo-4 AM, at baseline and during DG exposure. Responses of the spontaneous AP-induced Ca²⁺ transient cycle length (Fig. 7E) to DG were similar to those described above for APCL (Table 1). On average, the LCR period (Fig. 7D, Table 6) was reduced by 20.0% at 3.0 ± 0.4 min following DG exposure, from 307.2 ± 15.0 ms at baseline to 251.3 ± 14.2 ms (P < 0.05). The average spontaneous AP-induced Ca²⁺ transient cycle length (Fig. 7E, Table 6) at this time was reduced by 17.7%, from 364.6 ± 15.1 ms at baseline to 309.7 ± 15.7 ms (P < 0.05). At longer (9.5 ± 2.3 min) times of DG exposure, the average spontaneous AP-induced Ca²⁺ transient cycle length (Fig. 7E, Table 6) prolonged above its baseline by 33.8%, from 364.6 ± 15.1 ms at baseline to 464.8 ± 49.7 ms (P < 0.05). The average LCR period (Fig. 7D, Table 6) at this time was increased by 28.2% above its baseline, from 307.2 ± 15.0 ms at baseline to 373.7 ± 34.7 ms (P < 0.05).

Table 6.

Changes in LCR period and APCL in each individual SANC, measured by confocal microscopy at baseline and during DG exposure

Cell No.	Baseline LCR Period, ms	APCL, ms	Short LCR Period, ms	APCL, ms	Time in DG, min	Prolonged LCR Period, ms	APCL, ms	Time in DG, min
1	242.6	291.0	207.9	241.1	1	264.7	335.8	5
2	337.7	391.0	230.6	271.0	2	544.4	582.1	11
3	449.1	490.6	294.2	336.0	1	558.0	660.9	4
4	315.4	371.2	194.0	233.0	3
5	283.6	323.0				344.9	433.0	4
6	338.3	400.4	250.7	345.6	3
7	326.6	405.1	284.8	330.5	5
8	371.2	427.1	333.5	388.3	3
9	256.2	292.0				261.6	306.2	7
10	268.2	334.1	260.1	321.9	4	282.2	344.8	6
11	227.6	289.9				305.7	327.0	4
12	219.8	291.7	200.4	270.9	3	455.4	769.9	20
13	314.9	388.8	291.8	365.1	3	352.8	443.5	9
14	348.6	417.5	305.0	394.4	4	367.0	444.5	25
15	272.6	319.8	257.5	294.7	2
16	343.0	401.1	156.4	233.4	5
	307.2 ± 15.0	364.6 ± 15.1	251.±14.2*	309.7 ± 15.7*	3 ± 0.4	373.7 ± 34.7†	464.8 ± 40.7†	9.5 ± 2.3

Applicable values are means ± SE. Time was in minutes to achieve different stages of DG response.

^*P < 0.05 vs. baseline;

^†P < 0.05 vs. baseline and short via linear mixed-effects model to analyze repeated measurements (Bonferroni adjustment was made to the P values).

LCR, local diastolic Ca²⁺ release.

The average changes in other LCR parameters (size, duration, and amplitude of the Ca²⁺ signal of individual LCRs and of the LCR ensemble) at the aforementioned times during DG exposure are illustrated in Fig. 7, right. When the average spontaneous AP-induced Ca²⁺ transient cycle length and LCR period became reduced following DG exposure, as LCR size and LCR duration became increased (Fig. 7, F and G; P < 0.05), the Ca²⁺ signal of individual LCRs and the Ca²⁺ signal of LCR ensemble became larger (Fig. 7, H and I, P < 0.05). At longer times of DG exposure (9.5 ± 2.3 min), when the average LCR size decreased and the Ca²⁺ signal of individual LCRs and the Ca²⁺ signal of LCR ensemble became reduced, the spontaneous AP-induced Ca²⁺ transient cycle length and LCR period became prolonged. The average number of LCRs per cell (Fig. 7J) at this time decreased by about 40%, from 8.4 ± 0.3 s/100 μm at baseline to 4.7 ± 1.1 s/100 μm (P < 0.05), and LCRs became almost undetectable because of an increase of diastolic [Ca²⁺]_i (Tables 4 and 5).

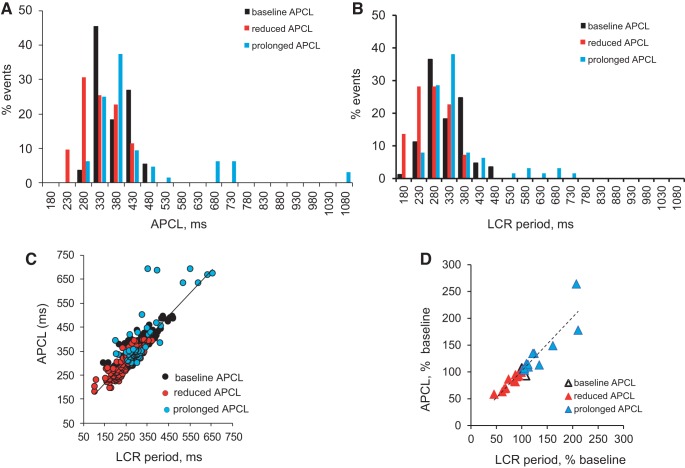
Figure 8A illustrates histogram distributions of APCLs (taken as the intervals between the peaks of 2 adjacent AP-triggered Ca²⁺ transients), and Fig. 8B illustrates histograms of the LCR period (measured as the time between the rapid upstroke of the prior AP-triggered Ca²⁺ transient and the onset of an LCR in diastole), measured in SANCs loaded with the Ca²⁺ indicator, fluo-4 AM, when APCL was reduced and prolonged in response to DG. Note that the histogram distributions of the LCR period and APCLs exhibited similar patterns in response to DG as distribution of APCL during continuous AP recordings (Fig. 5). Specifically, histograms of both the LCR period and APCLs when the average APCL and LCR period became reduced are skewed to the left of baseline and then shifted to the right when the average APCL and LCR period became prolonged with longer time of DG exposure.

Fig. 8.

Relationship and histograms of APCLs and LCR period at baseline and during DG exposure in intact SANCs by confocal microscopy. A and B: distributions of APCLs and LCR period in SANCs loaded with the Ca²⁺ indicator, fluo-4 AM (10 μmol/l), at baseline and times of DG exposure as in Fig. 7 (n = 347 events from n = ∼10–16 SANCs). C: relationship between individual LCR periods (measured as the time between the rapid upstroke of the prior AP-triggered Ca²⁺ transient and the onset of an LCR in diastole) and APCL (taken as the interval between the peaks of 2 adjacent AP-triggered Ca²⁺ transients) in SANCs loaded with the Ca²⁺ indicator, fluo-4 AM, at baseline and during DG exposure conforms to a line of identity (y = 0.9x + 73.1; r² = 0.8). D: relationship between the average APCL and the average LCR period in each cell for data shown in A and B. Data shown as a percent change of baseline (y = 1.2x − 11.6; r² = 0.9).

Relationship of DG-induced changes in the LCR period and changes in APCL.

Figure 8C illustrates all individual APCLs plotted against all LCR periods (n = 347 events) at baseline and at the time when APCL was reduced and prolonged during DG exposure. Figure 8D illustrates the relationship of the average APCL (percent change) to the average LCR period (percent change) among SANCs (n = ∼10–16 SANCs for each data point) during these times of DG exposure. As has been reported previously for a wide range of interventions that alter APCL (45, 51), a single monotonic function subtends all the points at baseline and during DG exposure even though the AP-induced Ca²⁺-transient cycle lengths and LCR periods exhibited biphasic changes from baseline, an early reduction followed by prolongation.

LCR characteristics in permeabilized SANCs.

To test whether DG has a direct effect on SR Ca²⁺ cycling that generates LCRs in the absence of Na⁺/K⁺ pump function, and in the absence of other surface membrane channel functions, we permeabilized individual SANCs with saponin and recorded LCRs in a physiological buffer with a free [Ca²⁺]_i of 100 nmol/l. Unlike intact SANCs (Fig. 7), following exposure to DG in permeabilized SANCs, there was no significant change in LCR characteristics (data not shown), as shown recently in permeabilized ventricular myocytes (1).

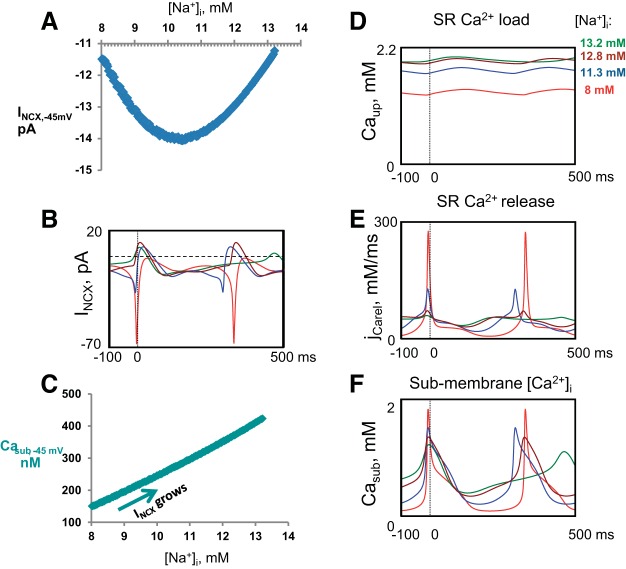
Numerical model simulations.

To get mechanistic insights into how [Na⁺]_i relegates the pacemaker cell system, we performed numerical model simulations within a broad [Na⁺]_i range from 6–14 mmol/l that included the landmarks of APCL changes, following DG exposure (as discussed above). It is important to note that we did not simulate [Na⁺]_i changes; rather [Na⁺]_i was an independent parameter in the model. Model simulations were performed at each given [Na⁺]_i via a slow [Na⁺]_i ramp clamp (0.075 mM/s). The slow ramp allowed the model to attain steady state for each [Na⁺]_i. We also tested slower ramps, as slow as 0.01 mm/s, i.e., 0.6 mm/min, similar to the experimentally measured rate of [Na⁺]_i change, but this did not change the results. Thus we performed numerical modeling to simulate how Na⁺-induced changes in cytosolic Ca²⁺, LCRs, and MDP regulate the APCL, i.e., SANC automaticity.

It is important to note that, although DG inhibits I_NaK, this is a minor factor in model simulations. Rather it is the DG-induced [Na⁺]_i rise that determines the model behavior observed experimentally. In our model equations, we have reduced the density of I_NaK in the presence of DG to 37.5% of control (parameter I_NaKmax from 2.88 to 1.08 pA/pF), in line with experimental data of I_NaK blockade by DG within the range of 24% to 38% reported previously for atrial responses at 36.5°C (49). Although our results are presented for the 37.5% of the initial I_NaKmax, we also tested model behavior with stronger I_NaKmax inhibition (to 25% of the initial value), but this did not change the results.

The model reproduced experimental results.

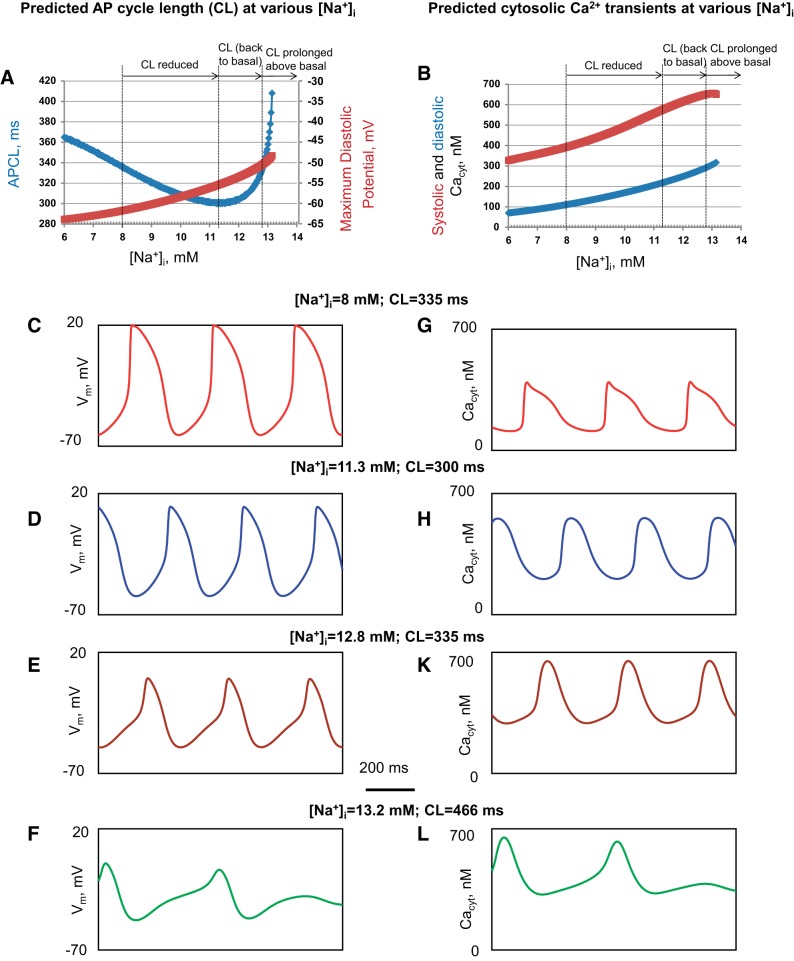
Model stimulations reproduced the biphasic average APCL changes (Fig. 9A, blue plot) observed experimentally (Fig. 3), as [Na⁺]_i increased within the experimentally measured continuum of [Na⁺]_i (Fig. 2). Examples of the APCL change over the continuum of [Na⁺]_i are illustrated in Fig. 9, C–F. The biphasic effect consisted of APCL reduction from 335 ms at 8 mmol/l [Na⁺]_i (at baseline, before DG, Fig. 9C) to a minimum of 300 ms at an [Na⁺]_i of 11.3 mmol/l (Fig. 9D); this was followed by an increase in APCL to return to the baseline level of 335 ms at 12.8 mmol/l (Fig. 9E). As [Na⁺]_i increased further, the simulated APCL prolonged above baseline (Fig. 9F); the AP firing subsequently became dysrhythmic and ceased as [Na⁺]_i increased higher than 13.2 mmol/l (Fig. 9A, blue plot), in close agreement with the experimental data (Figs. 3 and 4).

Fig. 9.

Numerical model simulations reproduce experimental effects of the DG-induced increase in [Na⁺]_i on SANC APCLs and Ca²⁺ transients. These effects occur concomitantly with a slow rise in [Na⁺]_i from 6 mmol/l to 14 mmol/l on the key system characteristics. A: APCL (blue plot) and MDP (dark red plot). B: systolic and diastolic cytosolic Ca²⁺ concentration (Ca_cyt, red and blue plot, respectively). C–F: representative APs (V_m) illustrated for 4 different [Na⁺]_i within the entire simulation range: baseline, minimum APCL, APCL prolongation back to baseline, and APCL prolongation above baseline. G–L: cytosolic Ca²⁺ transients (Ca_cyt) selected at reference points noted above for V_m.

Our model simulations also reproduced MDP changes observed experimentally (Fig. 3B); as [Na⁺]_i increased from baseline to 13 mmol/l, the MDP became progressively depolarized from −61.7 mV to −50.0 mV (Fig. 9A, dark red plot). Also, the model simulations reproduced experimentally observed changes of Ca²⁺ transients; the peak of the systolic Ca²⁺ signal amplitude (dark red curve in Fig. 9B) and diastolic [Ca²⁺]_i levels both increased (blue curve in Fig. 9B and simulated cytosolic Ca²⁺ transients in Fig. 9, G–L) as [Na⁺]_i increased, similar to that measured with Indo-1 (Fig. 6).

Insights via numerical simulations of electro-driving forces.

As we increased [Na⁺]_i in the model, MDP depolarized and intracellular levels of [Na⁺]_i and [Ca²⁺]_i increased. These factors ought to influence Na⁺ and Ca²⁺ equilibrium potentials E_Na = (RT/F)ln[Na⁺]_o/[Na⁺]_i and E_Ca = (RT/F)ln[Ca²⁺]_o/[Ca²⁺]_subspace and, importantly, their respective electrochemical driving forces V_m − E_Na, V_m − E_Ca. The driving forces for Na⁺ and Ca²⁺ obviously regulate respective selective Ca²⁺ and Na⁺ ion currents. We performed numerical model simulations of the driving forces to evaluate the scale of this regulation (Fig. 10A), taking advantage of model predictions of Ca²⁺ in the submembrane space (i.e., the space where Ca²⁺ is released by RyR and interacts with the NCX) (Fig. 11F), rather than using bulk cytosolic [Ca²⁺]_i measured experimentally by Indo-1 (Fig. 6).

Fig. 10.

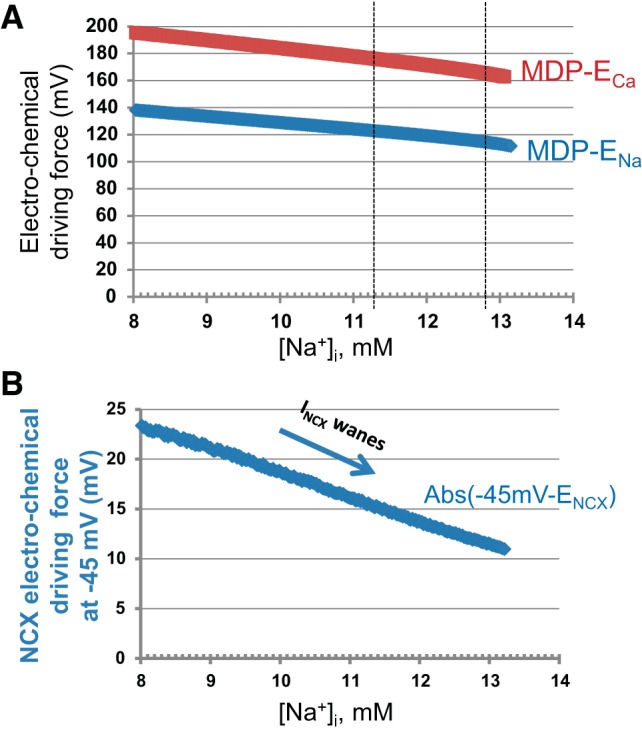
Model simulations of the electro-chemical driving forces in response to increase in [Na⁺]_i. A: changes of the electro-chemical driving force for Ca²⁺ (MDP − E_Ca, red plot) and Na⁺ (MDP − E_Na, blue plot). B: changes of the electro-chemical driving force for I_NCX at −45 mV (−45 mV − E_NCX).

Fig. 11.

Numerical model simulations provide mechanistic insights into I_NCX biphasic change that underlie the biphasic regulation of AP firing rate with [Na⁺]_i rising from 8 to 14 mmol/l. A: I_NCX amplitude changes at a key diastolic membrane potential of −45 mV, as a function of [Na⁺]_i. B: representative I_NCX waveforms at baseline, minimum APCL, APCL prolongation back to baseline, and APCL prolongation above baseline. C: illustration of the positive I_NCX regulation by submembrane Ca²⁺ (i.e., by ensemble of LCR Ca²⁺ signal). D–F: representative examples of simulated waveforms of free sarcoplasmic reticulum (SR) Ca²⁺ load, SR Ca²⁺ release flux, and submembrane Ca²⁺ concentration directly interacting with NCX. Colors representing different [Na⁺]_i match colors in Fig. 9. The overlapped traces are synchronized at the AP overshoot (vertical dashed lines).

As [Na⁺]_i increases, the shifts in E_Na and E_Ca, combined with MDP depolarization, indeed reduce Na⁺ and Ca²⁺ driving forces (Fig. 10A). However, the scale of the changes in each driving force alone is rather small, remaining within about 15% over 8.0–13.2 mmol/l of [Na⁺]_i increase. Thus it is difficult to expect a substantial regulation of a selective calcium current (I_CaL) or a selective sodium current (I_bNa) via just its driving force decrease alone.

On the other hand, E_NCX, the reversal potential for I_NCX, is determined, not just by either driving force alone, but by the difference between Ca²⁺ and Na⁺ gradients (2); E_NCX = 3E_Na − 2E_Ca. This ion-driving mechanism makes a crucial exceptional difference for how I_NCX changes in response to DG compared with other ion currents. A crucial submembrane Ca²⁺ level is that attained at the I_CaL activation threshold before the AP upstroke (at about −45 mV). Thus, when these factors are taken into consideration in calculating the change in the driving force for NCX at −45 mV over the range of [Na⁺]_i from 8.0 to 13.2 mM, the change in E_NCX is indeed substantially decreasing, by more than 50% (from 23.3 to 10.9 mV, Fig. 10B).

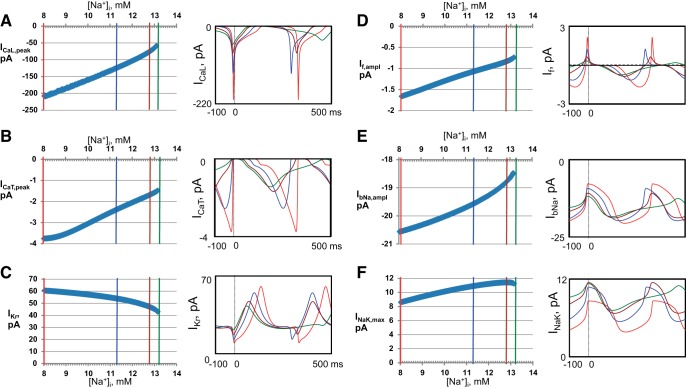
Further insights from numerical simulations of ion currents and Ca²⁺ dynamics.

Additional simulations provided insights for Na⁺ regulation of intrinsic Ca²⁺-, voltage-, and time-dependent ion current changes during AP firing that cannot be accessed experimentally (Figs. 11 and 12).

Fig. 12.

Insights gleaned using numerical model simulations on Na⁺ regulation of the cell membrane ion currents (via direct and indirect effects). Plots of continuous membrane current changes (left) for over the entire range of [Na⁺]_i from 8 to 14 mmol/l illustrated with their representative waveforms (right) at the 4 key [Na⁺]_i. Colors representing different [Na⁺]_i match colors in Fig. 9. The overlapped traces are synchronized at the AP overshoot (vertical dashed lines). A: L-type Ca²⁺ current (I_CaL). B: T-type Ca²⁺ current (I_CaT). C: rapid delayed rectifier K⁺ current (I_Kr). D: funny current (I_f). E: Na⁺ background current (I_bNa). F: Na⁺/K⁺ ATPase current (I_NaK, remaining after I_NaK inhibition by DG).

The simulated changes of I_NCX during diastole (at −45 mV, Fig. 11, A and B) showed the same biphasic behavior as for experimentally observed and model-simulated APCL. As [Na⁺]_i increased from 8.0 to 10.5 mmol/l, the magnitude of the diastolic I_NCX in the model simulations increased and then decreased as [Na⁺]_i continued to increase further to 13.2 mmol/l (Fig. 11B). The biphasic change in I_NCX occurs because of contributions of the two opposing forces; an increase in Ca_sub amplifies I_NCX (Fig. 11C), but the concurrent increase in [Na⁺]_i reduces I_NCX via a decrease in the NCX driving force (V_m − E_NCX) (Fig. 10B). The Na⁺-induced increase in Ca_sub in the model (Fig. 11F) is linked to a larger SR Ca²⁺ load (Fig. 11D), resulting in a larger diastolic SR Ca²⁺ release flux (j_Carel) (Fig. 11E), reflecting LCR ensemble Ca²⁺ signal (Fig. 7I). Furthermore, that the average LCR period is initially reduced in the model simulations (blue curve, Fig. 11E) is in good agreement with our experimental results, which demonstrate that the LCR period becomes initially reduced following DG exposure (Figs. 7 and 8, Table 6). As [Na⁺]_i increased further, diastolic j_Carel activated earlier, but its time course during DD (i.e., before AP-induced transient) became substantially prolonged, resulting in the integrated release occurring later in time, which was in line with the prolonged LCR period found experimentally at a longer time of DG exposure (Figs. 7 and 8).

The simulated peak l-type Ca²⁺ current (I_CaL) substantially decreases (by a factor of about 3) as [Na⁺]_i increases (Fig. 12A), attributable, in part, to the concomitant collapse of the Ca²⁺-driving force (dark red curve in Fig. 10A). The major factor of I_CaL decline, however, is linked to the Ca²⁺-induced Ca²⁺ inactivation as submembrane Ca²⁺ rises (Ca_sub, Fig. 11F). Specifically, the respective scaling factor (f_Ca) of I_CaL at the time of the I_CaL peak is 0.50 at 8 mmol/l [Na⁺]_i, but it is reduced to 0.24 at 13 mmol/l [Na⁺]_i. Both T-type Ca current (I_CaT) and the rapid delayed rectifier current (I_Kr) also decrease (Fig. 12, B and C) as MDP depolarizes, and AP amplitude concomitantly collapses. Both I_f and I_bNa (Fig. 12, D and E) decrease because of the reduction in the Na⁺-driving force (V_m − E_Na, Fig. 10A). However, the reduction of I_f is much greater than that of I_bNa because of I_f voltage-dependent kinetics; as MDP depolarizes (dark red plot in Fig. 9A), I_f voltage-dependent activation is concomitantly reduced (because I_f is activated by membrane hyperpolarization). The amplitude of I_f, however, is determined by the square of the I_f gating variable y in our model. Capturing this factor in our simulations, we found that this specific y² factor (at its peak) is substantially reduced in the model from 1.7% to 1.1% at 8 and 13 mmol/l [Na⁺]_i, respectively, indicating its major importance for the I_f decline in addition to the I_f decrease attributable to change in the driving force for Na⁺. The Na⁺/K⁺-ATPase (I_NaK) outward current (partially inhibited by DG) monotonically increased as [Na⁺]_i increased (Fig. 12F).

DISCUSSION

Using a combination of experimental and numerical modeling approaches, we determined how the coupling of Na⁺ and Ca²⁺, electrochemical gradients within the pacemaker cell coupled-clock system, regulates automaticity of single SANCs. We measured responses of [Na⁺]_i, [Ca²⁺]_i, membrane potential, and APCL and rhythm in rabbit SANCs to Na⁺/K⁺ pump inhibition by the digitalis glycoside, DG.

Our results indicate that even a small increase in [Na⁺]_i perturbs SANC automaticity via impacting numerous coupled-clock mechanisms that include, not only direct [Na⁺]_i and [Ca²⁺]_i changes (i.e., their gradients and respective driving forces), but also complex indirect effects attributable to clock coupling involving SR and sarcolemmal mechanisms. Specifically, DG, acting directly on the sarcolemmal Na⁺/K⁺ pump, not only produces a progressive increase in [Na⁺]_i and MDP depolarization, but also indirectly perturbs Ca²⁺ clock functionality (reflected in LCR changes) and induces alterations in I_CaL, I_CaT, I_f, I_NCX, I_NaK, I_bNa, and I_Kr, which result from the ensemble of the aforementioned DG effects.

Response to DG when [Na⁺]_i minimally increases.

A reduction in APCL is the initial response to DG that emerges in the context of a minimal [Na⁺]_i gain. The average 18% (P < 0.05) reduction in APCL in rabbit SANCs in response to DG occurs when [Na⁺]_i increases (on average) only by 5% (P < 0.05). This effect is indicative of high gain of [Na⁺]_i regulation of SANC automaticity as in ventricular myocytes (3, 11, 21, 22, 34). The average amplitude of Ca²⁺ transient increases, accompanied by the slight increase of diastolic [Ca²⁺]_i. We interpreted the acceleration of AP firing during the initial response to DG to be an extension of normal automaticity, i.e., a positive chronotropic response, analogous to the positive inotropic response to the small increase in [Na⁺]_i that alters SR Ca²⁺ loading in ventricular myocytes (5, 21, 22). In addition to a reduction of the average APCL that accompanied the initial small increase in [Na⁺]_i from 8.4 ± 0.4 mmol/l at baseline to 8.9 ± 0.1 mmol/l in the present study during early DG responses, the LCR period becomes reduced, and the average LCR size, the Ca²⁺ signal of the LCR ensemble, becomes increased. Furthermore, acceleration of DD occurs earlier during this stage of DG response, manifested by a reduced time to nonlinear DD part (Table 1, parameter TNLDD).

The early reduction in APCL in response to DG (Fig. 3) was strongly correlated with the reduction in the LCR period (Figs. 7 and 8). We interpret the reductions in APCL and the LCR period, the increase in LCR size and Ca²⁺ signal of LCR ensemble, and changes in other AP waveform parameters to indicate an increase in coupling of clock molecules that comprise the coupled-clock system (18, 26, 50). Because of clock coupling, direct and specific effects (pharmacological or genetic) on any single molecule of either clock inevitably impact the functions of all molecules that regulate V_m, E_Na, and E_Ca within the coupled-clock system. For example, the prolongation of the spontaneous SANC APCL by ivabradine, a specific I_f (funny current) blocker, had been exclusively attributed, in early studies, to its direct reduction in I_f (6, 53). More recent studies, however, clearly indicate that, because the ivabradine-induced APCL prolongation induced [Ca²⁺]_i reduction, ivabradine effects on APCL also indirectly involve a reduction in the Ca²⁺ clock function; thus the net APCL prolongation by ivabradine reflects a reduction in clock coupling (54). Therefore, the ivabradine effect on SANC APCL extends far beyond its direct effect on surface membrane ion channels, like DG in the present study.

Our experiments in permeabilized SANC bathed in physiological free [Ca²⁺]_i of 100 nmol/l demonstrated that DG was without significant effect on LCR characteristics, as shown recently in ventricular myocytes (1). Thus DG effects on the LCR period and APCL are due to a direct effect of Na⁺/K⁺ pump inhibition that induces an increase in [Na⁺]_i and reduction Ca²⁺ extrusion via NCX and therefore to changes in [Na⁺]_i and [Ca²⁺]_i.

The initial reduction in APCL to DG observed experimentally is predicted by our simulations of a coupled-clock pacemaker model (Fig. 9D) (26). The initial increases in [Na⁺]_i and [Ca²⁺]_i accelerate the kinetics of SR Ca²⁺ cycling, leading to a reduction in the average period of spontaneous LCRs, an increase in the amplitude of the ensemble of LCR Ca²⁺ signal, which occurs at an early time, leading to early and stronger I_NCX (Fig. 11B, blue plots), and to a reduction in the APCL. This is in good agreement with our experimental results (Fig. 7, D, E, and I). It is important to note that the APCL reduction happens despite a decrease in all major currents, including I_NCX, as E_Ca, E_Na, and E_NCX and their respective driving forces all decrease, indicating the complex nature of this APCL reduction effect, in which diastolic LCRs play the major role.

Please note the occurrence of these changes that accompanied a minimal increase in [Na⁺]_i by DG is also a manifestation of a tight clock coupling. The model simulation of [Ca²⁺]_i and other parameters contrasts strikingly with a prior simulation of a pacemaker function, in which an increase in [Na⁺]_i to 15 mM was required for [Ca²⁺]_i to impact on automaticity (27), which was interpreted to indicate that [Ca²⁺]_i is implicated in a dysrhythmic behavior. Thus [Ca²⁺]_i is implicated only in abnormal automaticity.

Transition from initial APCL reduction to APCL prolongation.

The initial experimentally measured reduction of the average APCL was followed by APCL prolongation back to baseline values, which was accompanied by an [Na⁺]_i increase to 12.0 ± 0.7 mmol/l (42%). The subsequent APCL prolongation above baseline to 420.0 ± 24.0 ms was accompanied by a further increase in [Na⁺]_i to 14.6 ± 1.2 mmol/l (73%) and a marked (2.5-fold) increase in APCLV (Table 3). The average LCR period became prolonged and less synchronized, and LCR occurrence became reduced (Figs. 7 and 8). As has been reported previously for a wide range of interventions that alter APCL (45, 51), a single monotonic function subtends all the points at baseline and during DG exposure, even though the APCLs and LCR periods exhibited biphasic changes from baseline, an early reduction followed by prolongation. Numerous prior studies have demonstrated that changes in APCL in response to different perturbations are linked to concurrent changes in LCR periods (i.e., times from the prior AP-induced Ca²⁺ transient upstrokes to the subsequent diastolic LCR occurrence) and in other LCR characteristics (18, 19, 54). The effects of DG, however, on the AP-induced Ca²⁺ transient cycle length and spontaneous LCRs during DD have not been described previously. As the LCR ensemble Ca²⁺ signal wanes and is delayed (Fig. 11E), the decrease in driving force for I_NCX (i.e., V_m − E_NCX) (Fig. 10B) becomes the dominating factor in APCL prolongation (Fig. 9A).

We interpreted the gradual prolongation of the average APCL and LCR period, the reduction in LCR size and Ca²⁺ signal of LCR ensemble, the prolongation of the average TNLDD and the MDP depolarization, increase in the variability of APCL and AP waveform parameters, and a further reduction in E_Na − E_Ca that accompanies [Na⁺]_i and [Ca²⁺]_i accumulations to reflect a reduction in coupling of clock molecules within the coupled-clock system.

Grossly dysrhythmic APCLs as [Na⁺]_i and [Ca²⁺]_i further increase, and MDP markedly depolarizes.

As the average [Na⁺]_i increased to 15.4 ± 1.7 mmol/l, the MDP became markedly reduced, APCLs became grossly dysrhythmic (684.0 ± 43.9 ms), APCLV increased to 8.3-fold above baseline (Table 3), and LCR became almost undetectable as diastolic [Ca²⁺]_i increased (Figs. 6 and 11F, Table 4). We interpreted this gross arrhythmic APCL stage of the response to DG to reflect marked clock uncoupling (41). The steep relationships between the degree of clock coupling and increase in [Na⁺]_i and reduction in E_Na − E_Ca (or change in 3E_Na − 2E_Ca) would appear to be an underpinning of the well-recognized narrow therapeutic:toxic ratio of DG compounds (31, 37).

Stereotyped responses of excitable cardiac tissue and cells to DG.

The pattern of APCL responses of single SANCs in the present study over a range of increases of [Na⁺]_i and [Ca²⁺]_i MDP depolarization, and a progressive reduction in E_Na and E_Ca over time following DG exposure, bears a striking resemblance to that measured in intact sinus node (SAN) tissue in response to a high DG concentration (39, 41). Specifically, in isolated SAN preparation, a response to a high DG concentration includes an initial reduction in APCL followed by a APCL prolongation and, with further time, marked arrhythmic behavior (DG toxicity emerges) (39, 41). In studies in SAN preparations in which incremental concentrations of DG rather than a single high DG dose are employed, the early reduction in APCL is not detected, i.e., only APCL prolongation is observed (32); in contrast, in single atrioventricular nodal cells in which a single DG dose was significantly higher than in the present study, only APCL reduction was detected followed by cell contracture at a longer time of DG exposure (13). Although, in these studies in multicellular SAN preparations, changes of [Na⁺]_i were not monitored and APCL changes over time were not related to [Na⁺]_i, E_Na − E_Ca, or E_NCX, the biphasic response to DG was observed. In the present study in single SANCs, the time course of [Na⁺]_i and [Ca²⁺]_i gain, MDP depolarization, and biphasic changes in APCL following DG exposure was heterogeneous among cells. However, because similar time-dependent changes in response to DG occur both in SAN tissue and single, isolated SANCs in the present study, this indicates that the pattern of changes in APCL is not an artifact related to isolation of SANCs from SAN tissue.

DG-induced heterogeneity of excitability in intact SAN tissue has been implicated in DG-induced SAN dysrhythmias (39, 41). The present study also discovered AP cycle variability, not only in APCL, but also in other parameters of the AP waveform (Table 3). The cycle-to-cycle variability within individual SANCs residing within SAN tissue may be implicated in DG-induced dysrhythmia in SAN tissue. The pattern of APCL changes over time as [Na⁺]_i increases in the present study following DG exposure also mimics the contractile responses of the intact heart, ventricular tissue, or isolated ventricular myocytes (VM); an increase in AP-induced phasic contraction initially occurs in response to small increase in [Na⁺]_i, followed by reduction in contraction (17, 34). As [Na⁺]_i and [Ca²⁺]_i continue to increase, and at longer times of exposure to DG as higher [Na⁺]_i and [Ca²⁺]_i levels are achieved, the amplitude of phasic contractions declines, spontaneous diastolic Ca²⁺ oscillations emerge, their summation elevates diastolic force, and abnormal action potential and arrhythmias occur (17). Thus, in response to a small increase in [Na⁺]_i and [Ca²⁺]_i induced by DG, the VM, isolated SAN tissue, and single SANCs all exhibit an initial positive inotropic, contractile, or chronotropic responses, respectively; at higher [Na⁺]_i and [Ca²⁺]_i, marked dysrhythmic response occurs in the VM, SAN tissue, and SANC. The full-spectrum stereotyped response patterns to DG can be obtained in any cardiac cells in the heart over short experimental times in response to a high DG concentration (as in the present study), or over longer times during exposure to DG at incremental (low to high) DG concentrations.

In summary, SANC automaticity is tightly regulated by E_Na, E_Ca, and E_NCX via a complex interplay of numerous key pacemaker mechanisms that regulate SANC clock coupling.

Limitations.

It is important to note that the aim of the study was to explore how complex, interrelated changes in [Na⁺]_i and [Ca²⁺]_i regulate the coupled-clock pacemaker system, rather than regulation of [Na⁺]_i homeostasis per se. Therefore, [Na⁺]_i was not simulated by the model, but the model was used to predict simultaneous changes in ion currents and E_Na, E_Ca, and E_NCX based on submembrane Ca²⁺ concentration changes rather than measured experimentally cytoplasmic [Ca²⁺]_i. Although our model closely reproduced essential features of the experimental results, a limitation of the model is that it is a common pool model type that reproduces only LCR ensemble Ca²⁺ signal rather than individual LCR Ca²⁺ signal. A more detailed examination of submembrane signals and local electrochemical driving forces will require future studies to use local Ca²⁺ SANC models, such as those recently developed (40).

Other intracellular responses that accompany the reduction in E_Na and E_Ca that were not measured in the present study merit investigation in future studies. These include Ca²⁺ activation of adenylyl cyclase (AC) and calcium/calmodulin-dependent protein kinase II (CAMKII), leading to changes in cAMP and phosphorylation states of Ca²⁺ cycling proteins, which impacts AP firing rate, and protein kinase C (PKC) activation, which has been implicated in the DG-evoked positive inotropic response in rat right atrial cells (33). Additionally, although not measured in the present study, the Na⁺/K⁺ pump is regulated by phospholemman phosphorylation (28), involving negative regulation by type 1 protein phosphatase inhibitor (12). When phosphorylated in ventricular myocytes by PKA and PKC, phospholemman stimulates the Na⁺/K⁺ pump to tightly regulate [Na⁺]_i and [Ca²⁺]_i. During β-adrenergic receptor stimulation of ventricular cells, an increase of phospholemman phosphorylation stimulates the Na⁺/K⁺ pump and limits an increase [Na⁺]_i, thus limiting [Ca²⁺]_i increase to [Ca²⁺]_i overload and thus preventing propensity to arrhythmias in the heart (28).

Changes in SANC energy metabolism linked to AC cAMP, PKA, and CAMKII that have recently been addressed in prototypic numerical pacemaker models (56) are not addressed in the present study. Likewise, changes in mitochondrial [Ca²⁺]_i accumulation (55) that occur in response to DG (because the mitochondrial uniporter competes with SERCA2 for Ca²⁺ via modulating the SR Ca²⁺ clock function) are not addressed in the present study. An increase in intracellular reactive oxygen species (ROS), induced by Ca²⁺-dependent or -independent DG effects on RyR, leads to changes in spontaneous RyR activation and SR Ca²⁺ load in ventricular myocytes (14). Furthermore, an increased [Na⁺]_i reduces mitochondrial [Ca²⁺]_i (8, 15, 23, 48), resulting in an increase of cytosolic NADH/NAD⁺ redox potential that alters sarcolemmal NCX activity independently of mitochondrial respiration by inhibiting I_NCX via NADH-induced cytosolic ROS and may also be involved in the SANC responses to DG observed in the present study. Finally, intracellular pH becomes reduced when Na⁺/K⁺ pump is inhibited (9, 42, 43), and this certainly impacts on numerous coupled-clock functions experimentally measured or numerically modeled in our study.

GRANTS

This work was supported by the Intramural Research Program of the NIH, National Institute on Aging.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.S. and E.G.L. conception and design of research; S.S., V.A.M., Y.Y., R.B., and D.Y. performed experiments; S.S., Y.Y., and R.B. analyzed data; S.S., V.A.M., and E.G.L. interpreted results of experiments; S.S., Y.Y., V.A.M., and R.B. prepared figures; S.S., V.A.M., and E.G.L. drafted manuscript; S.S., V.A.M., Y.Y., H.A.S., and E.G.L. edited and revised manuscript; S.S., V.A.M., Y.Y., R.B., D.Y., T.M.V., H.A.S., and E.G.L. approved final version of manuscript.