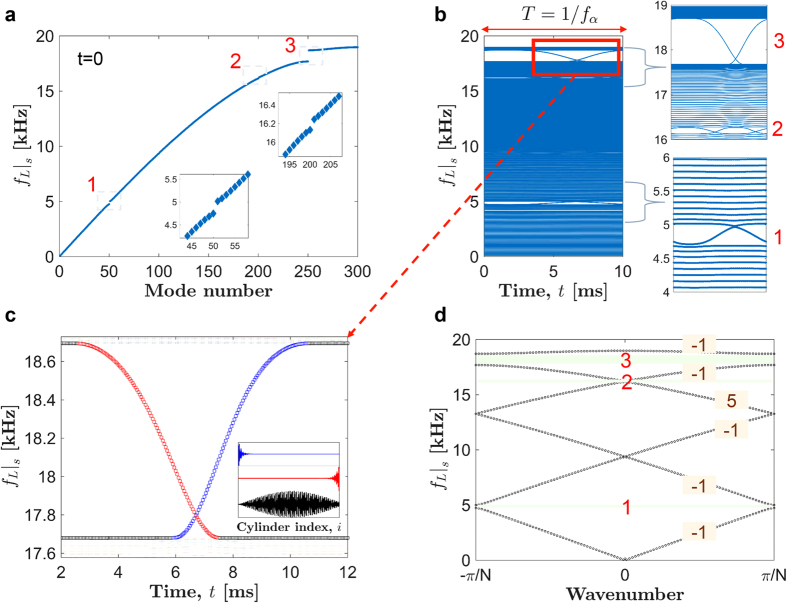
Figure 2. Non-trivial band-topology due to quasi-static torsional wave pumping.

(a) Spatio-temporal variation in stiffness, caused by torsional wave, forces the system’s eigen-frequencies for longitudinal vibration mode to change over time. We plot the eigen-frequencies of a finite size system at one such time instant highlighting the prominent band-gaps: 1, 2, and 3 (insets show zoomed view). (b) Evolution of eigen-frequencies over one period of pumping. Insets show close view of frequency evolution inside the band-gaps: 1, 2, and 3. The points of degeneracy (crossing) are noticeable. (c) A closer view of the degenerate point inside band-gap 3 showing that edge modes interchange their polarities across the degenerate point, a signature of bulk-boundary correspondence in topological transition. Inset shows the corresponding eigen-modes, both edge and global, represented in different colors. (d) Bloch dispersion curve of an infinitely periodic lattice, with Chern numbers assigned to each bands. Non-zero values of gap Chern numbers (summation of Chern numbers of the bands below) confirm the topological nature of all three prominent band-gaps.