Watching Populations Melt Down

Main Text

One of the curious features of Darwinian Evolution is that it requires errors to be made during genome replication. Otherwise, beneficial mutations could not occur and adaptation would arrest. Not surprisingly, however, random DNA copy errors usually do not lead to improvement—most mutations are deleterious or have little effect (1). Because, as far as we know, evolution has not found a way to selectively boost beneficial mutations, one wonders how large replication error rates could possibly be without overwhelming the population with deleterious mutations (2). This question of maximal sustainable mutation rates has fascinated theoretical evolutionary biologists for decades (2, 3), yet experimental results are scarce. Now, Max Lavrentovich (a theorist), Mary Wahl (an experimenter), and their colleagues (4) describe an elegant way to watch microbial populations on the verge of succumbing to deleterious mutants.

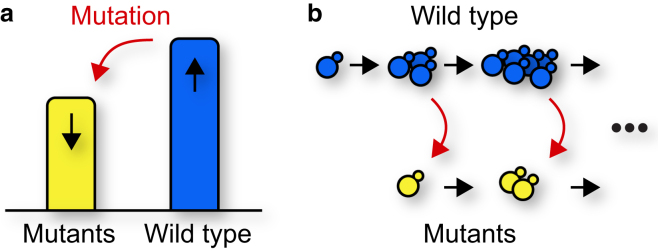
The simplest model for the trade-off between natural selection and deleterious mutations is illustrated in a two-state population model in Fig. 1. One-way mutations occurring at rate μ per generation supply a continuous flux from the wild-type to the mutant type. This flux is compensated by the wild-type growing 1 + s times faster than the mutant type. As a consequence, both types reach “mutation-selection balance” when the fraction of the mutant type is μ/s (5). Hence, if the rate of deleterious mutations is larger than their typical effect, the wild-type goes extinct and the mutants take over. If this process continues due to further deleterious mutations, the population is at risk of continuously accumulating deleterious mutations in a phenomenon called “mutational meltdown” (3) or “error catastrophe” (2) (for a discussion of these two terms and their differences, see Wilke (6)). Obviously, then, nature needs to ensure that mutation rates do not exceed the selective disadvantage of typical mutations to avoid the complete loss of the wild-type. Indeed, sophisticated error correction mechanisms are in place, which keep mutation rates below 10⁻⁹ per basepair in many organisms (7).

Figure 1.

(a) Mutation-selection balance and mutational meltdown: a fast-growing wild-type population accumulates deleterious mutations. If the mutation rate is too large, the population fitness declines continuously. (b) Experimental system used by Lavrentovich et al. (4): yeast wild-type cells (blue) stochastically convert to a slower-growing mutant type (yellow) at a slow, tunable rate. To see this figure in color, go online.

Many refinements of this idealized picture have been discussed in the literature, such as finite number fluctuations, a fitness effect distribution for mutations, and the effects of space. Nevertheless, there have been only a few attempts to actually study this threshold phenomenon in the lab (8), largely because a well-controlled experimental model system was missing.

Lavrentovich et al. (4) address this need by engineering a yeast strain that effectively mutates at a tunable rate to a less fit phenotype, whose selective disadvantage can also be independently tuned. To engineer a strain that spontaneously mutates toward a less fit type, they employ a genetic system for inducible genetic changes in yeast, first devised by Lindstrom and Gottschling (9). By only weakly inducing the mutations and changing their effect such that mutated daughter cells experience a (tunable) lower growth rate, Lavrentovich et al. (4) have now turned the approach into a powerful tool to study the process of mutational meltdown in the lab.

When grown in well-mixed liquid culture, the yeast populations of Lavrentovich et al. (4) conform to the predictions of classical mutation-selection balance theory: if the mutation rate is larger than the selective disadvantage of the mutants, the mutant type takes over; otherwise the population settles to some steady-state fraction of wild-type and mutants.

Interestingly, when growing the populations as colonies on solid media, Lavrentovich et al. (4) observe that the deleterious mutants fix in the population more readily, i.e., at smaller mutation rates and higher mutation cost. The underlying reason is that, even though the total population is quite large, there are strong number fluctuations at the edge of the growing colony. These fluctuations decrease the efficiency of selection and allow deleterious mutations to surf or even fix. As a result, mutational meltdown is harder to avoid, as hypothesized in earlier theoretical work (10, 11).

The experimentally observed scaling of the transition line between wild-type survival and extinction, corroborated by simulations and analytical arguments, is consistent with the directed percolation universality class (12). While, as the authors note, future theoretical work should explore additional biological features that could modify selection or genetic drift in microbial colonies or biofilms, such as surface roughness, three-dimensional structure, or motility, this minimal model rationalizes the observed behavior. This suggests further experiments and represents an intriguing application of a classical problem of nonequilibrium statistical physics to living systems.

Spatial structure thus promotes mutational meltdown, with important consequences for natural populations, which are often spatially organized. For instance, spontaneous mutations conferring antibiotic resistance, which are usually accompanied by a fitness cost, may be more abundant in biofilms and solid tumors than predicted by well-mixed population models. More fundamentally, a more stringent error threshold in spatially expanding biofilms could perhaps explain the unusually low mutation rates observed in bacteria (compared to higher eukaryotes (7))—it takes ∼1000 cell divisions for just a single mutation to occur anywhere in a bacterial genome.

But perhaps the most important contribution of this work is its innovative experimental approach: the ability to track individual spontaneous mutations over time and to control their rates of emergence and fitness effects could be adapted to other microbes and, perhaps, to multicellular model organisms. This would open the door to a new type of precision experiment in population genetics, offering an exciting tool to complement the successful and widespread genomics and experimental evolution approaches (13).

Editor: Zemer Gitai.