Abstract
Whereas it is known that elevated intraocular pressure (IOP) increases the risk of glaucoma, it is not known why optic nerve heads (ONHs) vary so much in sensitivity to IOP and how this sensitivity depends on the characteristics of the ONH such as tissue mechanical properties and geometry. It is often assumed that ONHs with uncommon or atypical sensitivity to IOP, high sensitivity in normal tension glaucoma or high robustness in ocular hypertension, also have atypical ONH characteristics. Here we address two specific questions quantitatively: Do atypical ONH characteristics necessarily lead to atypical biomechanical responses to elevated IOP? And, do typical biomechanical responses necessarily come from ONHs with typical characteristics. We generated 100,000 ONH numerical models with randomly selected values for the characteristics, all falling within literature ranges of normal ONHs. The models were solved to predict their biomechanical response to an increase in IOP. We classified ONH characteristics and biomechanical responses into typical or atypical using a percentile-based threshold, and calculated the fraction of ONHs for which the answers to the two questions were true and/or false. We then studied the effects of varying the percentile threshold. We found that when we classified the extreme 5% of individual ONH characteristics or responses as atypical, only 28% of ONHs with an atypical characteristic had an atypical response. Further, almost 29% of typical responses came from ONHs with at least one atypical characteristic. Thus, the answer to both questions is no. This answer held irrespective of the threshold for classifying typical or atypical. Our results challenge the assumption that ONHs with atypical sensitivity to IOP must have atypical characteristics. This finding suggests that the traditional approach of identifying risk factors by comparing characteristics between patient groups (e.g. ocular hypertensive vs. primary open angle glaucoma) may not be a sound strategy.
Keywords: lamina cribrosa, optic nerve head, biomechanics, glaucoma, sensitivity, stochastic modeling, IOP
1. Introduction
Glaucoma is the second leading cause of blindness worldwide (Quigley and Broman, 2006). Elevated intraocular pressure (IOP) has been identified as the main risk factor for the development and progression of the disease (Bengtsson and Heijl, 2005). Nevertheless, there is a wide range of sensitivity to elevated IOP, whereby some people suffer glaucoma at apparently normal levels of IOP (normotensive glaucoma) and others show no signs of the disease despite having elevated IOP (ocular hypertension) (Burgoyne et al., 2005; Quigley, 2005). The origin of this range of sensitivities to IOP is still not fully elucidated (Quigley, 2005). A common notion has been that the sensitivity to IOP of a specific optic nerve head (ONH) is determined, at least in part, by its biomechanical characteristics, namely the mechanical properties and geometry of the ONH tissues (Albon et al., 1995; Grytz et al., 2012; Reis et al., 2012; Sigal and Ethier, 2009; Wu et al., 2015). From this perspective, some eyes have a specific characteristic or a combination of characteristics that render them particularly sensitive to IOP and more likely to develop glaucoma, or particularly resilient to IOP and present as ocular hypertensive. This view has fueled efforts to characterize the morphology and biomechanics of eyes with various forms of glaucoma, which are then compared with those of normal and ocular hypertensive eyes in the hope that it will be possible to identify a structural or biomechanical biomarker for the disease (Coudrillier et al., 2015; Jonas et al., 2013; Lee and Kim, 2015; Omodaka et al., 2015; Park et al., 2015; Pijanka et al., 2014; Pijanka et al., 2015; Roberts et al., 2010).
Underlying the studies mentioned above is the assumption that ONHs that have an uncommon or atypical sensitivity to IOP, be it high sensitivity or high robustness, also have atypical ONH characteristics. Based on our recent observations of the complex nonlinear interactions between factors influencing ONH biomechanical sensitivity to IOP (Sigal, 2009, 2011; Sigal et al., 2012; Sigal et al., 2011), we suspect that this assumption might not hold true.
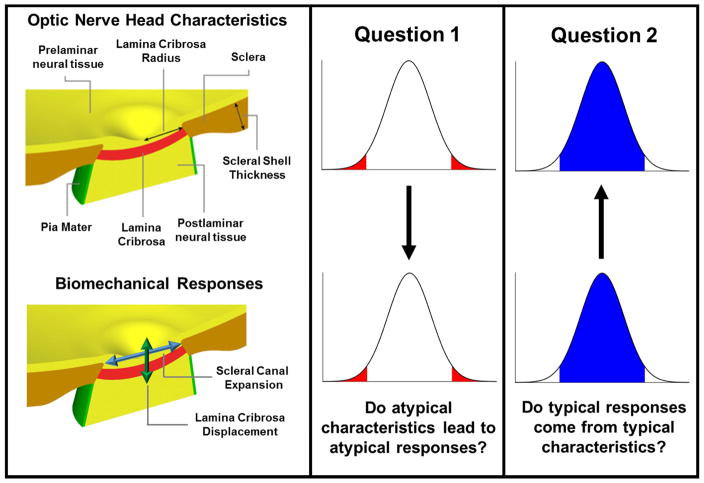
In this study, we used a large set of models representing ONHs with a wide range of characteristics spanning anatomy/geometry and tissue mechanical properties to address two specific questions: (1) Do atypical ONH characteristics, necessarily lead to atypical biomechanical responses to IOP? And (2) Do typical biomechanical responses to IOP necessarily come from typical ONH characteristics? (Fig. 1) We defined typical to mean a characteristic or response with a value close to the median of the population of ONHs, and atypical for a value that is distant to the median. We studied how the threshold used to define typical vs. atypical affected the answer to the questions. A negative answer would indicate that simply splitting ONHs into typical or atypical based on their characteristics or responses is not a good approach for determining susceptibility to glaucoma.
Figure 1.
Schematic of the research questions. We produced 100,000 different ONH models with random but carefully selected characteristics according to the normal distributions in Table 1. Example geometric parameters are shown on the top left panel. We simulated the response of each ONH model to a 10 mmHg increase in IOP. Four aspects of these responses were obtained for each ONH (Table 2). These included the anterior-posterior lamina displacement and the scleral canal expansion (bottom left panel). Characteristics and response values were classified as typical or atypical. Using the ONH population and their responses we addressed quantitatively two research questions (middle and rightmost columns): (1) Do atypical ONHs (those with all atypical characteristics) necessarily lead to atypical responses to IOP? (2) Do typical biomechanical responses necessarily come from typical ONH characteristics? The graphs represent the distributions of characteristics (top) or responses (bottom), classified into typical (blue) or atypical (red).
2. Methods
2.1. Population of Simulated ONHs
In order to have a well-controlled and large population of ONHs that would provide statistically robust results, we used a population of 100,000 ONH models from a previously published study (Sigal et al., 2012). The ranges and distributions for the characteristics corresponded to normal subjects and were based on the literature (Table 1) (Sigal et al., 2005; Sigal et al., 2004). Note that atypical characteristics were still within the normal ranges. The ONH models were generated using Gaussian distributions of 8 characteristics of interest which had been identified as contributing to more than 96% of the variation in IOP-induced ONH displacements, deformations and forces among 21 characteristics (Sigal, 2009). The geometric characteristics that were varied were the radius of the eye, the thickness of the sclera, the radius of the lamina cribrosa (LC) and the anterior-posterior position of the central LC. The mechanical properties of the ONHs that were varied were the elastic modulus of the LC, the elastic modulus of the sclera, the elastic modulus of the neural tissue, and the Poisson’s ratio of the neural tissue. The Poisson’s ratio defines the compressibility of the tissue and was intended to account for the potential for fluid displacements, including axoplasmic flow. It should be noted that we use the term mechanical properties solely to refer to the intrinsic material mechanical properties and not the structural or geometric properties.
Table 1. Distribution of Characteristic Values.
ONH models were assigned characteristics (tissue mechanical properties and geometries) following normal distributions based on the literature, as detailed elsewhere (Sigal et al., 2012).
| Characteristic | Median | SD | Min | 2.5th % | 97.5th % | Max |
|---|---|---|---|---|---|---|
|
Geometry
| ||||||
| Eye Radius (μm) | 12000 | 800 | 9600 | 10500 | 13600 | 14400 |
| Scleral Thickness (μm) | 800 | 53.0 | 640 | 697 | 903 | 960 |
| LC Radius (μm) | 950 | 63.3 | 760 | 827 | 1070 | 1140 |
| LC Position (μm) | 100 | 33.3 | 0.115 | 35.1 | 165 | 200 |
|
| ||||||
| Mechanical Properties | ||||||
|
| ||||||
| LC Modulus (MPa) | 0.5 | 0.133 | 0.1 | 0.241 | 0.758 | 0.9 |
| Scleral Modulus (MPa) | 5.0 | 1.33 | 1.0 | 2.42 | 0.757 | 9.0 |
| Neural Tissue Modulus (MPa) | 0.05 | 0.0133 | 0.01 | 0.0241 | 0.0757 | 0.09 |
| Neural Tissue Compressibility | 0.45 | 0.015 | 0.4 | 0.421 | 0.478 | 0.49 |
As before, the mechanical response of a given ONH model to an IOP elevation of 10 mmHg was calculated using a published surrogate cubic polynomial model derived from our earlier finite element models of the ONH (Sigal et al., 2012). In this study we analyzed four components of the mechanical response (Table 2): the maximum tensile strain within the LC (the 95th percentile maximum principal strain) (Sigal et al., 2005), scleral canal expansion (SCE), lamina cribrosa displacement (LCD), and the laminar median von Mises stress (a non-directional measure of the force per unit area in the LC) (Sigal et al., 2005).
Table 2. Distribution of ONH Biomechanical Responses.
The following values characterize the distribution of responses to an IOP increase of 10 mmHg for the entire population of ONH models.
| Response | Median | SD | Min | 2.5th % | 97.5th % | Max |
|---|---|---|---|---|---|---|
| Maximum Principal Strain (%) | 0.802 | 0.210 | 0.429 | 0.566 | 1.38 | 2.61 |
| Scleral Canal Expansion (μm) | 3.45 | 1.17 | 1.36 | 2.20 | 6.72 | 15.2 |
| Lamina Cribrosa Displacement (μm) | 7.64 | 2.72 | −9.11 | 2.98 | 14.1 | 31.3 |
| Mean Von Mises Stress (kPa) | 6.10 | 1.78 | 1.56 | 3.31 | 10.4 | 19.2 |
2.2. Definition of Typical
As a first approach we classified characteristics and responses as typical or atypical using a binary definition based on a hard percentile threshold. Specifically, we defined a typical characteristic or response as one that fell between the 2.5 and 97.5 percentiles. An atypical characteristic or response was thus defined as one falling outside that range, i.e. being in the extreme 5%. For clarity, we refer to this cutoff value as the 5% atypicality threshold. All characteristics were equally sampled using the same threshold. This simple definition allowed us to directly address our two research questions. We then repeated the analysis varying the atypicality threshold from 0 to 100%. Finally, we investigated the dependence of the conclusions on the use of a rigid binary threshold by using instead a smoothly varying probability parameter representing “typicality” with values between 0 and 1 according to its percentile distance to the median. The conclusions were independent of the threshold value, or the use of hard or smoothly varying typicality. For briefness, we present the results of the smooth typicality analysis in the Appendix.
2.3. Data Analysis
To answer the first question, do atypical ONH characteristics necessarily lead to atypical biomechanical responses, we examined the responses of ONHs with a given atypical characteristic, and calculated the percentage of ONHs that had any atypical response using the 5% atypicality threshold. We also examined ONHs with 1 or more, 2 or more, 3 or more, and 4 or more atypical characteristics and calculated the percentage that had atypical responses. We compared these percentages to the percentage of ONHs with any atypical response found in the whole population of models. We repeated this analysis with atypicality thresholds ranging from 0 to 100%.
To address the second question, do typical biomechanical responses necessarily come from ONHs with typical characteristics, we examined ONHs with only typical biomechanical responses and calculated the percentage that arose from ONHs with a particular atypical characteristic. To examine the effect of a 5% atypicality threshold, we repeated the calculation of percentages using atypicality thresholds from 0 to 50%.
Whereas the analyses described above answer directly and quantitatively the two questions of interest, they are not visual. To get a better sense of what our findings mean for ONH biomechanics we examined scatterplots of the SCE and LCD for all ONHs.
Analyses were done with the software package R (v2.12.0) (R Core Team, 2013) and with Matlab (v2015a, Mathworks).
3. Results
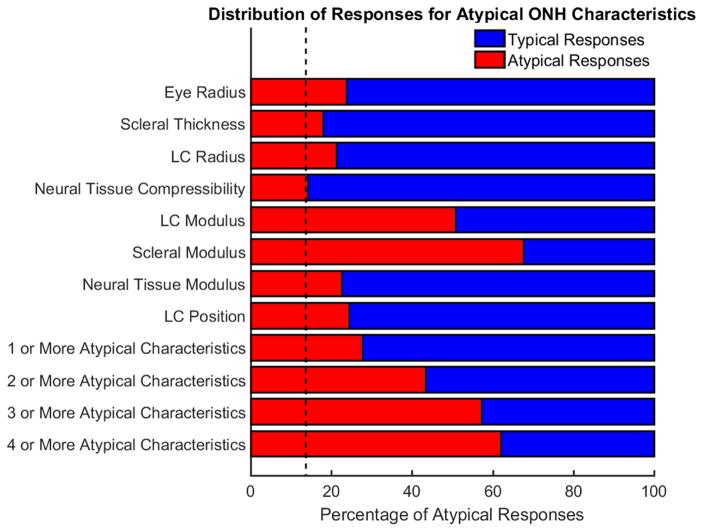
Using a 5% atypicality threshold we found that 34% of all ONHs had at least one atypical input characteristic, but only 14% of ONHs had at least one atypical mechanical response. Hence not all atypical ONH characteristics result in atypical responses to IOP. It should be noted that 34% corresponds to one minus the expected value for having 8 independent characteristics be typical (1-(1-t)8=0.34 for t=0.05, where t is the atypicality threshold). The percentage of typical and atypical responses arising from ONHs with atypical characteristics appears in Figure 2. The analysis reveals not just that ONH’s with atypical characteristics can have typical responses, but most ONH’s with atypical characteristics have typical responses. Only the two strongest determinants of ONH mechanics, atypical LC moduli and scleral moduli (as previously observed (Sigal, 2009)), led to atypical responses more often than typical responses. For all other characteristics, the percentage of atypical responses arising from a specific atypical characteristic ranged from 14% to 25%.
Figure 2.
Atypical ONH characteristics usually lead to typical biomechanical responses. The red bars indicate the percentage of ONHs with the specified atypical characteristics that have atypical responses. The blue bars display the percentage of ONHs with the specified atypical characteristics that have typical responses. The black dashed vertical line represents the percentage of ONHs with an atypical mechanical response in the entire population (14%). A red bar that stops at the dashed line indicates that the characteristic has a weak influence on whether the response is typical or atypical. A longer red bar indicates that the factor has a stronger influence on the typicality of the response. Note that the analysis for the eight individual characteristics include ONHs where other characteristics are atypical in addition to the one specified. The presence of the blue regions indicates that atypical ONH characteristics do not necessarily lead to atypical responses, meaning that the answer to question one is no. This plot was computed with a typicality threshold of 95%.
The analysis of the characteristic combinations revealed that having one or more atypical characteristics was associated with an atypical response in 28% or roughly 1 out of every 4 cases. ONHs with four or more atypical characteristics had atypical responses in just 62% of cases. An ONH with four or more unspecified atypical characteristics was actually less likely to produce an atypical response than an ONH having an atypical scleral modulus. For comparison, 6% of ONH with no atypical characteristics had an atypical response. These results demonstrate that most ONHs with atypical characteristics did not have an atypical response, answering no to our first research question.
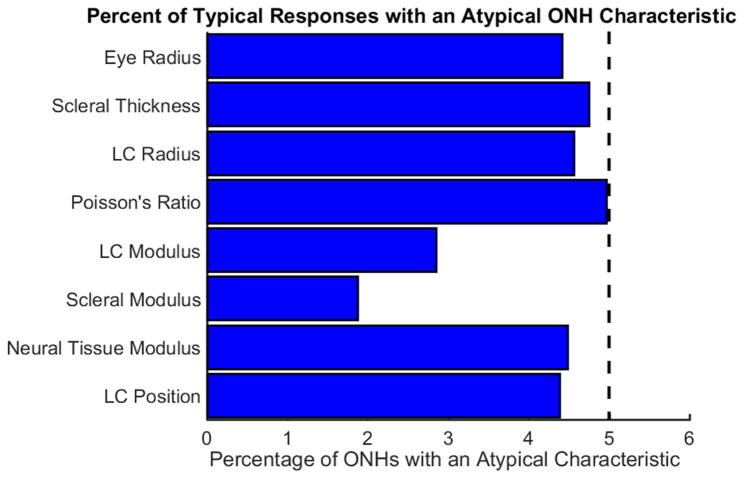
Moving now towards the second question, the percentage of typical and atypical biomechanical responses arising from atypical characteristics is shown in Figure 3. The blue bars representing the percentage of typical responses originating from ONHs with specific atypical characteristics demonstrate that between 2 and 5% of typical responses come from ONHs with a specified atypical characteristic. While this value appears low, it should be noted that only 5% of the entire population has a specified atypical characteristic, hence a value of 5% is what would be expected if a characteristic had no influence on whether a response was typical or atypical. This demonstrates that typical biomechanical responses did not necessarily arise from typical ONH’s..
Figure 3.
Typical biomechanical responses arise from ONHs with atypical characteristics. The blue bars indicate the percent of the population of ONHs with typical biomechanical responses that also have the specified atypical characteristics. The black dashed vertical line represents the percentage of ONHs with a specific atypical characteristic in the entire population. For most cases, the percentage of typical responses having a specified atypical characteristic was similar to the percentage of ONHs with that specified characteristic in the population as a whole. The fact that the percentages are non-zero indicates that the answer two question two is no. This plot was computed with a typicality threshold of 95%.
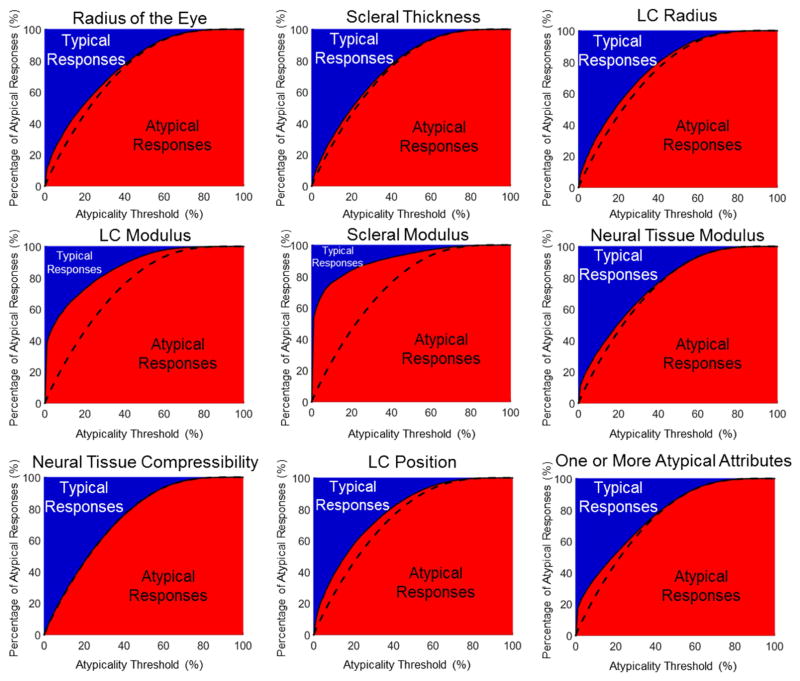
To this point, our analysis was done with a hard, arbitrarily chosen threshold to distinguish typical from atypical. To examine whether the choice of threshold may have influenced the answer to question one, we calculated the percentage of typical and atypical responses arising from ONHs with a particular atypical characteristic using atypicality thresholds ranging from 0 to 100% (Figure 4). For all the characteristics, a blue region in the upper left hand corner of the plots can be observed, which represents typical biomechanical responses resulting from atypical ONH characteristics. Only when the atypicality threshold is defined as 90% or higher does the proportion of atypical responses go to 100%. Thus, for any reasonable choice of threshold, the answer to question one remains no.
Figure 4.
Atypical ONH characteristics lead to typical biomechanical responses for nearly all choices of the atypicality threshold. The charts above display the distribution of responses (typical or atypical) for ONHs with the specified atypical characteristics over a range of atypicality thresholds. The plots are similar to the bars in Figure 2, a vertical cross section at 5% of any of the charts in Figure 4 would be identical to the bar plots in Figure 2. The dashed lines represent the percentage of the whole population with at least one atypical response at each atypicality threshold, and are identical in all panels. Plots where the red/blue interface closely matches the dashed line indicate that that characteristic has a weak influence on whether or not the response is typical or atypical. The presence of a blue region in the chart for all atypicality thresholds less than 90% indicates that the choice of a particular threshold did not alter the answer to question 1.
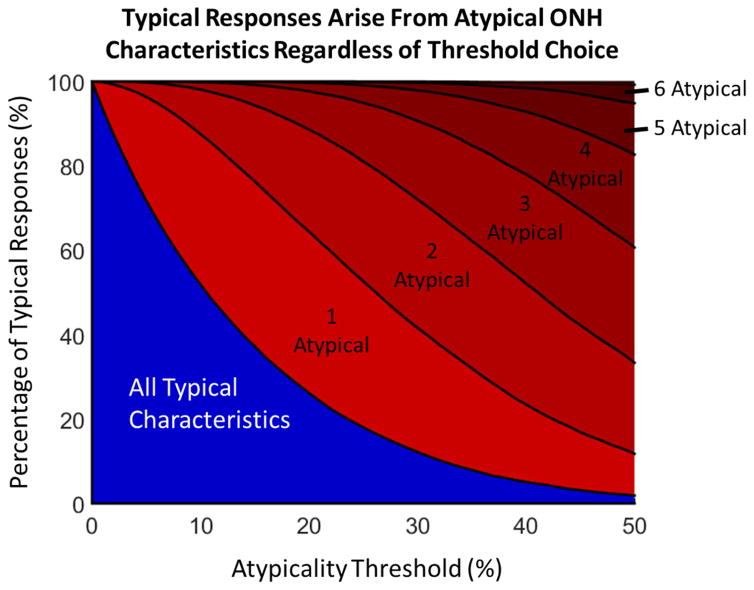
To examine the influence of our choice of the 5% atypicality threshold on the answer to question two, we calculated the percentage of typical ONH responses that arose from ONHs with a particular number of atypical characteristics (Figure 5). The effects of the individual parameters was relatively small, and therefore we report only the combinations. If the plot had been entirely blue it would demonstrate that typical biomechanical responses only arise from typical ONH characteristics. Instead the plot shows a large red region representing typical ONH responses arising from atypical characteristics, demonstrating that the choice of the atypicality threshold does not change our finding that typical responses frequently arise from ONH’s with atypical characteristics.
Figure 5.
Typical biomechanical responses arise from ONHs with atypical characteristics regardless of the atypicality threshold. The chart displays the percentage of ONHs with typical responses with a given number of atypical characteristics. The blue region represents the percentage of typical responses that come from ONHs with no atypical characteristics. The height of the red regions represents the percentages of typical responses that come from ONHs with one or more atypical characteristics. For example, at an atypicality threshold of 10%, only about half of all typical responses come from ONHs with no atypical characteristics, while roughly 40% of typical responses have 1 atypical characteristic and 10% have two or more. The presence of a red region at all atypicality thresholds indicates that our choice of atypicality threshold did not affect our conclusion that the answer to question 2 is no.
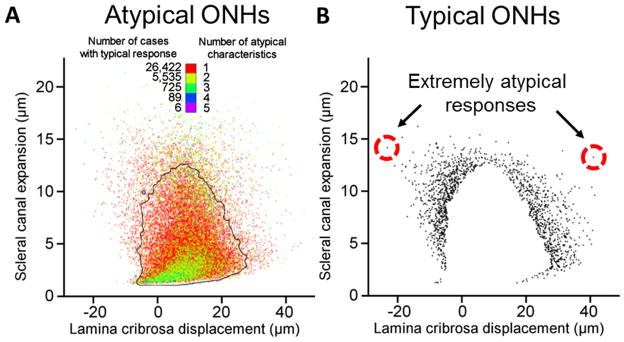
The scatterplots of Figure 6 depict the SCE and LCD of all ONH models, with points representing the individual responses of the ONH model. Figure 6A shows that the population of ONH models with atypical characteristics have responses that still cluster towards the median behavior. In other words, not only did atypical ONH characteristics frequently lead to typical responses, they lead to highly typical responses. Conversely, Figure 6B displays the mechanical responses of all ONHs with typical characteristics and atypical responses. Whereas responses do tend to concentrate near the 95% typicality boundary, there are several extreme cases, a couple of which we have highlighted. These two cases demonstrate that an ONH with all typical characteristics can, nevertheless, have highly atypical responses to IOP.
Figure 6.
Biomechanical response distributions. A. The distribution of scleral canal expansion (SCE) and lamina cribrosa displacement (LCD) responses for ONHs classified as atypical (having one or more atypical characteristic). The points are colored by the number of atypical characteristics for that ONH. The black outline represents the 2D 5% atypicality threshold, calculated as the smallest region containing 95% of all responses (Sigal and Grimm, 2012). To decrease plot saturation the pixel intensity is proportional to the number of points overlapping. This means that points in regions with few responses appear dim, whereas the central regions with many points appear dense. It is seen that even for ONHs with multiple atypical characteristics, there is a strong tendency towards the median response (the dense green region of the plot). B. The atypical SCE and LCD responses of ONH models with all typical ONH characteristics is shown. To ease visualization of isolated points we did not vary point intensity. To avoid plot saturation we therefore did not plot the cases with typical responses, which caused the white region in the center. Although it is seen that the responses of most ONHs do cluster near the threshold, there are several ONHs located very far from the typical response (circled in red).
4. Discussion
Our results demonstrate that the answers to both our questions are no: ONHs with atypical characteristics do not necessarily have atypical biomechanical responses to IOP. In fact, most ONHs with atypical characteristics have typical responses nonetheless. Likewise, typical biomechanical responses do not necessarily stem from typical ONH characteristics, with over a quarter of all typical responses arising from ONHs with at least one atypical characteristic.
For clarity, this study focused on whether atypical characteristics lead to atypical biomechanical responses, and whether typical biomechanical responses necessarily arise from typical characteristics. It should be noted, that the two questions as presented are not mutually exclusive. A negative answer to question one would ensure a negative answer to question two. However, a positive answer to question one would not ensure a positive answer to question two. We could have formulated instead questions such as can ONHs with atypical characteristics have typical biomechanical responses, and can typical ONH biomechanical responses arise from ONHs with atypical characteristics. In this case our study would demonstrate that the answers to these questions are yes, and that these phenomenon occur frequently.
This study is an extension of our previous analysis, (Sigal et al., 2012) in which we demonstrated that the ONH is a highly robust system, with a wide distribution of ONH characteristics leading to a concentrated distribution of responses. However, that analysis did not link together individual ONH characteristics to their responses. It could have been that atypical characteristics still led only to responses on the edges of the “narrow” distribution, or that typical responses were all from ONHs also in the central part of the characteristic distributions.
The answers to our research questions are important because they relate to the bigger questions: what is a “normal” ONH? And, how can one predict whether an ONH will have an abnormal sensitivity to IOP? Before we discuss this, we want to address our choice of the word typical. We considered several alternative words, including normal/abnormal, healthy/unhealthy, standard/non-standard, inlier/outlier and unremarkable/remarkable. There is likely no single word choice that will satisfy everyone. In our opinion the word typical best connotes proximity to the median without further inferences, and is therefore appropriate if its use is clearly defined.
Considering that we analyzed 100,000 ONHs, some readers might not be surprised that we found cases where a typical response could arise from an atypical ONH, and vice-versa. However, our quantitative approach allowed us to demonstrate that this can occur with surprisingly high frequency, independent of the threshold used to separate typical from atypical. If this was the case in our highly simplified deterministic mechanical modeling where all variables are known and precisely defined, it seems reasonable to expect an even more complex situation in patients. The fact that typical characteristics frequently lead to atypical responses implies that perhaps there is no “typical” ONH. This is important clinically, rigid cutoff values are often used to diagnose and monitor patients. It is also important to determine the mechanisms that lead to or contribute to development or progression of glaucoma. Our results show that the measurement of an atypical ONH geometry does not ensure atypical biomechanical sensitivity to IOP, and similarly atypical IOP-induced deformations do not necessarily imply atypical tissue properties. By sorting eyes into typical or atypical categories many sensitive eyes will be missed, and many stable eyes will be subjected to unnecessary screening.
Proper characterization of glaucoma susceptible eyes will require careful consideration of all the factors and their interactions. Even if one were to focus solely on the characteristics with the strongest influence on the biomechanical response, the elastic modulus of the LC and sclera, about a third of the population would still be mischaracterized, highlighting the combined effects of the other characteristics, including the geometric parameters To further complicate the matter, the LC and scleral modulus cannot be directly measured in the clinical setting (Girard et al., 2015), an issue we have addressed in our recent work (Sigal et al., 2014). Although the specificity of the LC and sclera moduli are not overly high, technologies that measure and track changes in scleral or LC modulus clinically may still be useful tools for predicting glaucoma progression. The development of screening metrics that consider the combined effects of multiple characteristics and interactions would be beneficial to explaining why some patients present as ocular hypertensives with no symptoms of glaucoma and some present with primary open angle glaucoma with normal levels of IOP.
The numerical model we used is the most comprehensive model, in terms of parameters considered, directly developed to capture the interaction between the geometric and mechanical characteristics of the eye, and we believe it is a useful representation of ONH mechanics. The model, however, is still a gross simplification of the actual ONH. The geometries are highly simplified and the mechanical properties are isotropic and linear. A thorough discussion of the limitations of this modeling approach can be found in our previous studies.(Sigal, 2009; Sigal et al., 2012; Sigal et al., 2005; Sigal et al., 2004; Sigal et al., 2007; Sigal et al., 2014) While these simplifications may not capture some of the complex local behavior of the ONH response to elevated IOP, they provide a reasonable estimate while allowing for large numbers of simulations to be performed, improving our general understanding of ONH biomechanics. It is possible that the simplifications of this model prevent the identification of other characteristics with strong influences on the real-world biomechanical responses of the ONH to elevated IOP. Work is ongoing within our lab and elsewhere to create improved computational models that capture the anisotropy, non-linearity, and inhomogeneity of the ONH (Coudrillier et al., 2013; Grytz et al., 2012; Zhang et al., 2015). However, with a more complex model, it would be nearly impossible to analyze 100,000 different ONHs. The simplicity and low computational overhead of the model allowed us to answer questions and provide insight that cannot be addressed through experiment alone. The overall ONH behavior described by the model is in reasonably good agreement with other models and experimental measurements, giving us confidence in the general trends in the model (Agoumi et al., 2011; Coudrillier et al., 2013; Grytz et al., 2012; Levy and Crapps, 1984; Roberts et al., 2010; Yan et al., 1994; Yang et al., 2009). Another limitation of this work is that we only examined a small change in IOP, 10 mmHg, while clinically IOP may be elevated to much higher levels. Given the linear mechanical properties of this model we find it best to limit the change in IOP to a small range. Linear models provide useful insight into the behavior of the ONH at normal levels of IOP. At elevated levels of IOP, the nonlinear material properties would more strongly influence the mechanical behavior of the ONH system. Future models will incorporate non-linear mechanical properties to study effects of elevated IOPs.
We chose the distribution of characteristics for our population of ONHs based on data obtained from normal eyes, with both typical and atypical characteristics within normal ranges. The distributions of characteristics in diseased eyes are often different from normal eyes, and it is possible that using values different from normal will change the associations between ONH attributes and responses. However, our work demonstrates that even for the simpler population of normal ONHs, the responses are complex and IOP sensitivity is difficult to predict.
It is worth noting that our analysis did not distinguish between characteristics that render an ONH atypically sensitive to elevated IOP or atypically insensitive. Defining what characteristic values lead to biomechanical stability and which lead to biomechanical sensitivity is extremely difficult as the interactions between characteristics may contribute more to the response than the characteristics themselves. Our previous work has investigated in depth the concept of biomechanical stability and shown that biomechanical stability arises from wide ranges of geometric and material characteristics (Sigal et al., 2012). Similar to this limitation is the fact that our analysis uses the same threshold to define typical across all characteristics and responses. In practice, it may be better to use strict thresholds for some parameters and more liberal thresholds for others. It is also important to consider that the ONH characteristics were selected independently from each other. We considered this reasonable in the absence of robust data supporting associations between characteristics. However, it is possible that the characteristics are correlated with each other. An example of this characteristic codependence is the negative correlation of sclera thickness with sclera modulus, which has been noted in ex-vivo inflation studies of monkey sclera (Girard et al., 2011; Girard et al., 2009). This interaction works to maintain effective scleral rigidity, demonstrating a natural tendency towards biomechanical stability (Girard et al., 2009). While not much is known about other ONH biomechanical covariates, it is certainly possible that some covariations are antagonistic, thus increasing the likelihood of an atypical response.
This study highlights the difficulties of predicting eye-specific sensitivity to IOP and susceptibility to glaucoma. We have demonstrated that seemingly typical ONH characteristics can lead to atypical biomechanical responses to elevated IOP, sometimes extremely atypical. In other words, even though the risk is low, it is possible for ONHs with characteristics within the normal range, to have atypical responses to IOP. Conversely, we have demonstrated that the robust system behavior of the ONH allows for ONHs with atypical characteristics to maintain typical biomechanical sensitivity to IOP.
Highlights.
We simulated the effects of IOP on 100,000 models of the optic nerve head, and studied the relationship between a model having typical/atypical attributes and having a typical/atypical response to IOP.
Optic nerve heads with atypical attributes frequently had typical response to elevated IOP.
Optic nerve heads with atypical responses to elevated IOP often had typical attributes.
The traditional approach of identifying risk factors of glaucoma by comparing attributes between patient groups (e.g. ocular hypertensive vs. primary open angle glaucoma) may not be a sound strategy.
Acknowledgments
Grant Information: Supported in part by National Institutes of Health grant R01-EY023966, R01-EY025011, R01-EY013178, P30-EY008098 and T32-EY017271 (Bethesda, MD), and the Eye and Ear Foundation (Pittsburgh, PA).
Appendix: Smooth Typicality Analysis
Elsewhere in this paper we have treated ONH characteristics as binary, being either typical or atypical. This means that characteristics that are only slightly different, but falling on opposite sides of the binary threshold, are treated as very different. For the analysis in this appendix we used a smooth and continuous definition of typicality instead of the hard, discrete definition (Figure A1). For this, we smoothly parameterized the distributions of all eight ONH characteristics listed in the paper and eleven biomechanical responses: the median 1st and 3rd LC principal strains, the maximum (95th percentile) LC 1st and 3rd principal strain, the median LC shear strain, the maximum LC shear strain, scleral canal expansion (SCE), LC displacement (LCD), LC thinning, median LC Von Mises stress, and maximum LC Von Mises stress. Typicality was parameterized so that values ranged between 0 (most atypical) and 1 (most typical) and all characteristics or responses were weighted equally.
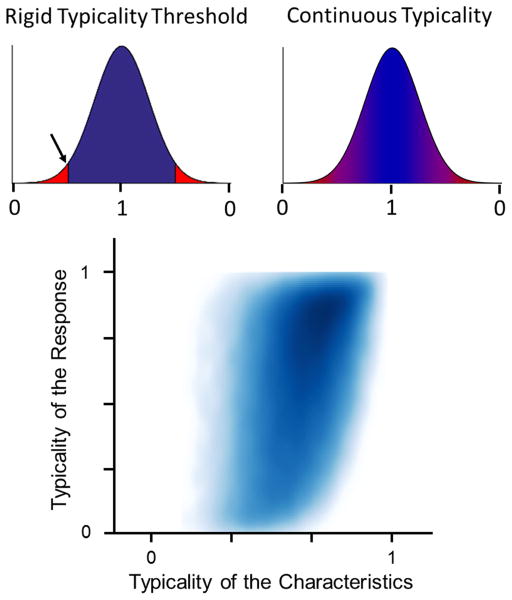
Figure A.1.
Smooth typicality distribution. (Top Left) Typicality defined using a rigid threshold is problematic as similar values on opposite sides of the threshold (arrow in plot) are considered to be vastly different. (Top Right) To address this issue, we parameterized the characteristics and responses to create a continuous definition of typicality. This parameterization was based on the area between the characteristic value and the median in the distribution curve, such that a characteristic with a value of the median had a continuous typicality of 1 and a characteristic with a value far away from the median was assigned a typicality approaching 0. We calculated ONH characteristic typicality as the eighth root of the product of the eight individual characteristics typicalities. Similarly ONH response typicality was calculated as the eleventh root of the product of all eleven response typicalities. (Bottom) The combined characteristic typicality vs. response typicality density plot is shown. The plot shows a continuous gradient of density that increases moving towards the top right of the plot. The plot also demonstrates that atypical characteristic typicalities (those near the left side) have a broad range of response typicalities. The plot shows a continuous gradient of density with the majority of points being located near the top right corner of the typicality space, consistent with the idea that higher characteristic typicality was somehow associated with higher response typicality.
The bottom panel of Figure A1 is a density plot of the continuous characteristic and response typicalities for all ONHs. The plot does not show a simple association between the typicality of a characteristic and the typicality of the response, which would appear as a narrow dense band. Instead, the blue blob is smooth and spread. This indicates that for a given characteristic typicality a wide range of response typicalities may occur, and conversely, a given response typicality may arise from a wide range of characteristic typicalities. This analysis confirms what was observed using the discrete thresholds elsewhere in this work: that atypical characteristics do not necessarily lead to atypical responses and that typical responses do not necessarily arise from typical characteristics, again answering no to both research questions
Footnotes
Proprietary Interest: None
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agoumi Y, Sharpe GP, Hutchison DM, Nicolela MT, Artes PH, Chauhan BC. Laminar and prelaminar tissue displacement during intraocular pressure elevation in glaucoma patients and healthy controls. Ophthalmology. 2011;118:52–59. doi: 10.1016/j.ophtha.2010.05.016. [DOI] [PubMed] [Google Scholar]
- Albon J, Karwatowski WS, Avery N, Easty DL, Duance VC. Changes in the collagenous matrix of the aging human lamina cribrosa. Br J Ophthalmol. 1995;79:368–375. doi: 10.1136/bjo.79.4.368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson B, Heijl A. A long-term prospective study of risk factors for glaucomatous visual field loss in patients with ocular hypertension. J Glaucoma. 2005;14:135–138. doi: 10.1097/01.ijg.0000151683.04410.f3. [DOI] [PubMed] [Google Scholar]
- Burgoyne CF, Downs JC, Bellezza AJ, Suh JK, Hart RT. The optic nerve head as a biomechanical structure: a new paradigm for understanding the role of IOP-related stress and strain in the pathophysiology of glaucomatous optic nerve head damage. Prog Retin Eye Res. 2005;24:39–73. doi: 10.1016/j.preteyeres.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Coudrillier B, Boote C, Quigley HA, Nguyen TD. Scleral anisotropy and its effects on the mechanical response of the optic nerve head. Biomech Model Mechanobiol. 2013;12:941–963. doi: 10.1007/s10237-012-0455-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coudrillier B, Pijanka JK, Jefferys J, Sorensen T, Quigley HA, Boote C, Nguyen TD. Effects of Age and Diabetes on Scleral Stiffness. Journal of biomechanical engineering. 2015 doi: 10.1115/1.4029986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJ, Dupps WJ, Baskaran M, Scarcelli G, Yun SH, Quigley HA, Sigal IA, Strouthidis NG. Translating ocular biomechanics into clinical practice: current state and future prospects. Curr Eye Res. 2015;40:1–18. doi: 10.3109/02713683.2014.914543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJ, Suh JK, Bottlang M, Burgoyne CF, Downs JC. Biomechanical changes in the sclera of monkey eyes exposed to chronic IOP elevations. Invest Ophthalmol Vis Sci. 2011;52:5656–5669. doi: 10.1167/iovs.10-6927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJA, Downs JC, Bottlang M, Burgoyne CF, Suh JKF. Peripapillary and posterior scleral mechanics--part II: experimental and inverse finite element characterization. Journal of biomechanical engineering. 2009;131:051012. doi: 10.1115/1.3113683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grytz R, Sigal IA, Ruberti JW, Meschke G, Downs JC. Lamina Cribrosa Thickening in Early Glaucoma Predicted by a Microstructure Motivated Growth and Remodeling Approach. Mechanics of materials : an international journal. 2012;44:99–109. doi: 10.1016/j.mechmat.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonas JB, Nangia V, Wang N, Bhate K, Nangia P, Nangia P, Yang D, Xie X, Panda-Jonas S. Trans-lamina cribrosa pressure difference and open-angle glaucoma. The central India eye and medical study. PLoS One. 2013;8:e82284. doi: 10.1371/journal.pone.0082284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee EJ, Kim TW. Lamina Cribrosa Reversal after Trabeculectomy and the Rate of Progressive Retinal Nerve Fiber Layer Thinning. Ophthalmology. 2015;122:2234–2242. doi: 10.1016/j.ophtha.2015.07.020. [DOI] [PubMed] [Google Scholar]
- Levy NS, Crapps EE. Displacement of optic nerve head in response to short-term intraocular pressure elevation in human eyes. Arch Ophthalmol. 1984;102:782–786. doi: 10.1001/archopht.1984.01040030630037. [DOI] [PubMed] [Google Scholar]
- Omodaka K, Horii T, Takahashi S, Kikawa T, Matsumoto A, Shiga Y, Maruyama K, Yuasa T, Akiba M, Nakazawa T. 3D evaluation of the lamina cribrosa with swept-source optical coherence tomography in normal tension glaucoma. PLoS One. 2015;10:e0122347. doi: 10.1371/journal.pone.0122347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SC, Brumm J, Furlanetto RL, Netto C, Liu Y, Tello C, Liebmann JM, Ritch R. Lamina cribrosa depth in different stages of glaucoma. Invest Ophthalmol Vis Sci. 2015;56:2059–2064. doi: 10.1167/iovs.14-15540. [DOI] [PubMed] [Google Scholar]
- Pijanka JK, Kimball EC, Pease ME, Abass A, Sorensen T, Nguyen TD, Quigley HA, Boote C. Changes in scleral collagen organization in murine chronic experimental glaucoma. Invest Ophthalmol Vis Sci. 2014;55:6554–6564. doi: 10.1167/iovs.14-15047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pijanka JK, Spang MT, Sorensen T, Liu J, Nguyen TD, Quigley HA, Boote C. Depth-dependent changes in collagen organization in the human peripapillary sclera. PLoS One. 2015;10:e0118648. doi: 10.1371/journal.pone.0118648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quigley HA. Glaucoma: macrocosm to microcosm the Friedenwald lecture. Invest Ophthalmol Vis Sci. 2005;46:2662–2670. doi: 10.1167/iovs.04-1070. [DOI] [PubMed] [Google Scholar]
- Quigley HA, Broman AT. The number of people with glaucoma worldwide in 2010 and 2020. Br J Ophthalmol. 2006;90:262–267. doi: 10.1136/bjo.2005.081224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2013. [Google Scholar]
- Reis AS, O’Leary N, Stanfield MJ, Shuba LM, Nicolela MT, Chauhan BC. Laminar displacement and prelaminar tissue thickness change after glaucoma surgery imaged with optical coherence tomography. Invest Ophthalmol Vis Sci. 2012;53:5819–5826. doi: 10.1167/iovs.12-9924. [DOI] [PubMed] [Google Scholar]
- Roberts MD, Sigal IA, Liang Y, Burgoyne CF, Crawford Downs J. Changes in the biomechanical response of the optic nerve head in early experimental glaucoma. Investigative Ophthalmology and Visual Science. 2010;51:5675–5684. doi: 10.1167/iovs.10-5411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA. Interactions between geometry and mechanical properties on the optic nerve head. Investigative Ophthalmology and Visual Science. 2009;50:2785–2795. doi: 10.1167/iovs.08-3095. [DOI] [PubMed] [Google Scholar]
- Sigal IA. An applet to estimate the IOP-induced stress and strain within the optic nerve head. Investigative Ophthalmology and Visual Science. 2011;52:5497–5506. doi: 10.1167/iovs.10-7141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Bilonick RA, Kagemann L, Wollstein G, Ishikawa H, Schuman JS, Grimm JL. The optic nerve head as a robust biomechanical system. Invest Ophthalmol Vis Sci. 2012;53:2658–2667. doi: 10.1167/iovs.11-9303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Ethier CR. Biomechanics of the optic nerve head. Experimental eye research. 2009:799–807. doi: 10.1016/j.exer.2009.02.003. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Ethier CR. Factors influencing optic nerve head biomechanics. Investigative ophthalmology & visual science. 2005;46:4189–4199. doi: 10.1167/iovs.05-0541. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Finite element modeling of optic nerve head biomechanics. Investigative ophthalmology & visual science. 2004;45:4378–4387. doi: 10.1167/iovs.04-0133. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR. Predicted extension, compression and shearing of optic nerve head tissues. Experimental eye research. 2007;85:312–322. doi: 10.1016/j.exer.2007.05.005. [DOI] [PubMed] [Google Scholar]
- Sigal IA, Grimm JL. A few good responses: Which mechanical effects of IOP on the ONH to study? Investigative Ophthalmology and Visual Science. 2012;53:4270–4278. doi: 10.1167/iovs.11-8739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Grimm JL, Schuman JS, Kagemann L, Ishikawa H, Wollstein G. A method to estimate biomechanics and mechanical properties of optic nerve head tissues from parameters measurable using optical coherence tomography. IEEE Transactions on Medical Imaging. 2014;33:1381–1389. doi: 10.1109/TMI.2014.2312133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal IA, Yang H, Roberts MD, Burgoyne CF, Crawford Downs J. IOP-induced lamina cribrosa displacement and scleral canal expansion: An analysis of factor interactions using parameterized eye-specific models. Investigative Ophthalmology and Visual Science. 2011;52:1896–1907. doi: 10.1167/iovs.10-5500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Xu G, Weinreb RN, Yu M, Leung CK. Optic Nerve Head Deformation in Glaucoma: A Prospective Analysis of Optic Nerve Head Surface and Lamina Cribrosa Surface Displacement. Ophthalmology. 2015;122:1317–1329. doi: 10.1016/j.ophtha.2015.02.035. [DOI] [PubMed] [Google Scholar]
- Yan DB, Coloma FM, Metheetrairut A, Trope GE, Heathcote JG, Ethier CR. Deformation of the lamina cribrosa by elevated intraocular pressure. Br J Ophthalmol. 1994;78:643–648. doi: 10.1136/bjo.78.8.643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Downs JC, Sigal IA, Roberts MD, Thompson H, Burgoyne CF. Deformation of the normal monkey optic nerve head connective tissue after acute IOP elevation within 3-D histomorphometric reconstructions. Invest Ophthalmol Vis Sci. 2009;50:5785–5799. doi: 10.1167/iovs.09-3410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Albon J, Jones H, Gouget CLM, Ethier CR, Goh JCH, Girard MJA. Collagen Microstructural Factors Influencing Optic Nerve Head Biomechanics. Investigative Ophthalmology & Visual Science. 2015;56:2031–2042. doi: 10.1167/iovs.14-15734. [DOI] [PubMed] [Google Scholar]