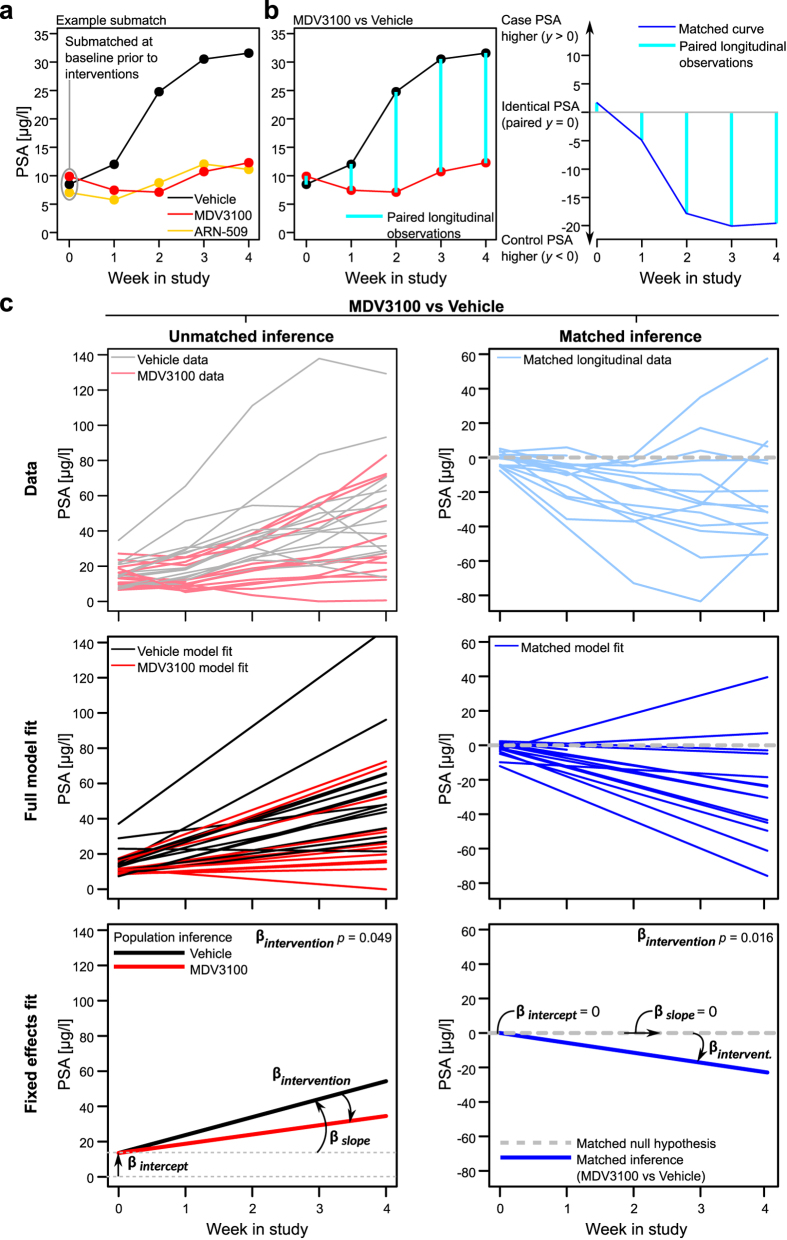
Figure 3. Statistical testing of the treatment effects using pairwise matched inference.

(a) The matched inference makes use of the baseline matching information when testing the intervention effects by pairing the observed responses according to the optimal submatches at equal time points. (b) An example of the submatch-based pairing in the MDV3100 vs vehicle comparison, where the example trajectory was previously shown as a single estimate value in the original study²³. Complex response differences are better captured when additional baseline information is incorporated into the statistical inference. The paired differences from the longitudinal observations (left panel) construct a single treatment curve for the pairwise matched mixed-effects modelling (right panel). (c) Comparison of the matched and unmatched statistical inference approaches in the MDV3100 vs vehicle comparison. Even if both inference approaches yield rather similar conclusion about the possible intervention effects, the matched approach improves the sensitivity of the detection (right panel). Different aspects of the mixed-effects modelling are visualized based on the observed data (top panel): the full model fit combining both the random and fixed effects (middle panel), and the population inference depicting only the fixed effects along with their interpretation (bottom panel). In the matched inference, the population of paired differences in the intervention effects (β_intervention) is tested against a null hypothesis of no paired differences (y = 0 line). The statistical inference results of the intervention effects are summarized in Table 1, and the full model fits for the four treatment cases are shown in Supplementary Figs S5 and S6.