FIG. 6.

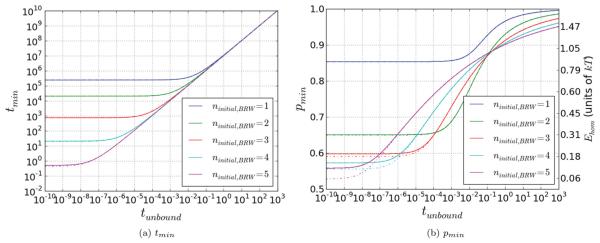
(Color) Optimized search. In (a), we obtain the minimal values of t_tot as a function of tunbound, by minimizing the curves shown in Fig. 5. The lines from top to bottom are for n_initial,BRW = 1 through 5, respectively. As expected, for low values of t_unbound, the difference in time is quite pronounced, with higher n_initial,BRW leading to faster execution. However, as t_unbound is increased, the difference between the various curves becomes less and less pronounced. In (b), we plot the corresponding minimizing values of p_hom, and the respective values for E_hom, as a function of t_unbound. In all cases, increasing t_unbound forces higher values of p, because of the increased incentive for higher r_H. For the same reason, all values for p_min approach 1 as t_unbound becomes very large. For low values of t_unbound, the curves also approach constant values. In this regime, the optimal p is determined by the trade-off between 1/r_H and t_het, without any influence by t_unbound. The curves were calculated using an absorbing boundary at n_step,BRW = 10,30,40. They are given by the dash-dotted, solid, and dashed lines, respectively. Note that the differences are very small, and especially between n_step,BRW = 30 and 40 are unnoticeable.