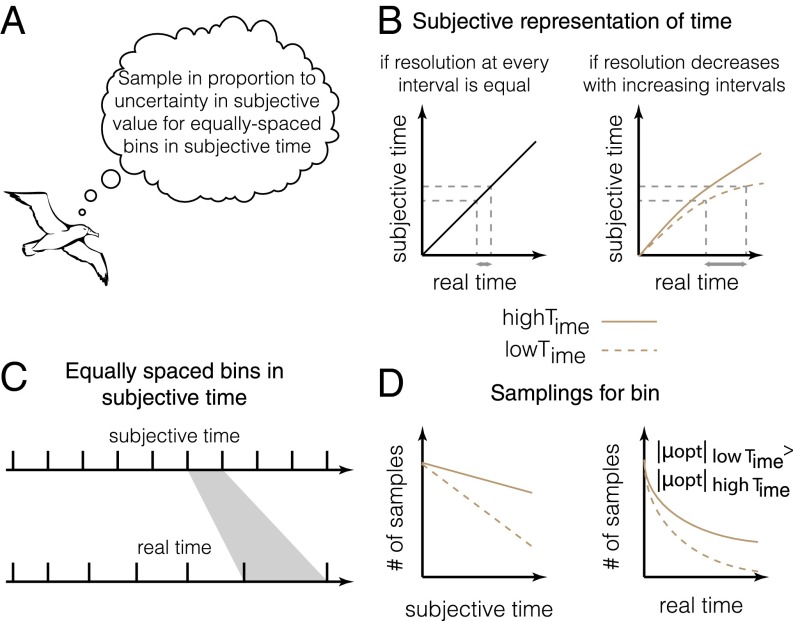
Fig. 4.
Optimal exploration when temporal representations are noisy. (A) Optimal algorithm for exploration. (B) If temporal resolution is constant at every interval, subjective representation of time can be represented as a linear function of real time, with constant noise. However, it is known that errors in timing increase with the interval being timed (42). In this case, subjective representation of time can be represented as a nonlinear function with the nonlinearity controlled by the parameter Time (43–45). (C) When subjective representation of time is nonlinear (concave), equal bins in subjective time correspond to bins of increasing width in real time. (D) A theory of reward rate maximization (43–45) predicts linear sampling for optimal exploration in subjective time, with the slope determined by Time. In real time, this sampling becomes hyperbolic (Eq. 3) with its decay controlled by Time (SI Results, 2.1.5) Exploration under noisy temporal estimation).