Tonotopic Optimization for Temporal Processing in the Cochlear Nucleus

Abstract

In the auditory system, sounds are processed in parallel frequency-tuned circuits, beginning in the cochlea. Auditory nerve fibers reflect this tonotopy and encode temporal properties of acoustic stimuli by “locking” discharges to a particular stimulus phase. However, physiological constraints on phase-locking depend on stimulus frequency. Interestingly, low characteristic frequency (LCF) neurons in the cochlear nucleus improve phase-locking precision relative to their auditory nerve inputs. This is proposed to arise through synaptic integration, but the postsynaptic membrane's selectivity for varying levels of synaptic convergence is poorly understood. The chick cochlear nucleus, nucleus magnocellularis (NM), exhibits tonotopic distribution of both input and membrane properties. LCF neurons receive many small inputs and have low input thresholds, whereas high characteristic frequency (HCF) neurons receive few, large synapses and require larger currents to spike. NM therefore presents an opportunity to study how small membrane variations interact with a systematic topographic gradient of synaptic inputs. We investigated membrane input selectivity and observed that HCF neurons preferentially select faster input than their LCF counterparts, and that this preference is tolerant of changes to membrane voltage. We then used computational models to probe which properties are crucial to phase-locking. The model predicted that the optimal arrangement of synaptic and membrane properties for phase-locking is specific to stimulus frequency and that the tonotopic distribution of input number and membrane excitability in NM closely tracks a stimulus-defined optimum. These findings were then confirmed physiologically with dynamic-clamp simulations of inputs to NM neurons.

SIGNIFICANCE STATEMENT One way that neurons represent temporal information is by phase-locking, which is discharging in response to a particular phase of the stimulus waveform. In the auditory system, central neurons are optimized to retain or improve phase-locking precision compared with input from the auditory nerve. However, the difficulty of this computation varies systematically with stimulus frequency. We examined properties that contribute to temporal processing both physiologically and in a computational model. Neurons processing low-frequency input benefit from integration of many weak inputs, whereas those processing higher frequencies progressively lose precision by integration of multiple inputs. Here, we reveal general features of input-output optimization that apply to all neurons that process time varying input.

Introduction

Sensory neurons compute and represent features of stimuli with meaningful patterns of action potentials. Information is represented in firing rates, temporal patterns, or both. Neuronal output is determined by both synaptic connectivity and intrinsic properties of the neurons themselves. In many regards, parsing the relative contributions of each can be difficult due to stimulus ambiguity or circuit complexity. Here we investigated cochlear nucleus neurons in the chicken, where synaptic inputs are limited in number and whose activity patterns are highly predictable from the stimulus waveform.

Auditory stimuli are processed in parallel frequency-tuned circuits, beginning in the cochlea (Galambos and Davis, 1943; Rose et al., 1959), where frequency is represented topographically. At low frequencies, auditory nerve (nVIII) fibers spike at a particular phase of the stimulus period, a response property known as phase-locking, which encodes temporal features of the stimulus (Gerstein and Kiang, 1960; Rose et al., 1967; Sachs et al., 1974). Chicken hearing ranges from 10 to 5000 Hz (Gray and Rubel, 1985; Warchol and Dallos, 1989; Saunders and Salvi, 1993), and phase-locking is observed at frequencies ≤3200 Hz, despite stimulus periods as brief as ∼300 μs (Salvi et al., 1992; Fukui et al., 2006). Frequency tuned nVIII fibers then impart “tonotopic” organization onto the cochlear nucleus magnocellularis (NM) (Rubel and Parks, 1975; Parks and Rubel, 1978; Jackson et al., 1982).

NM expresses many adaptations enabling phase-locking across a broad frequency range and at high firing rates. Large axosomatic synapses drive high firing rates and resist short-term synaptic depression (Parks, 1981; Raman and Trussell, 1992; Zhang and Trussell, 1994a, b; Oline and Burger, 2014). Additionally, short membrane time constants arise from prominent expression of low voltage-activated potassium channels (K_LVA). These channels activate with mild depolarization and provide a shunting conductance that limits summation of asynchronous inputs while lowering input resistance (Reyes et al., 1994; Rathouz and Trussell, 1998; Fukui and Ohmori, 2004; Lu et al., 2004; Slee et al., 2005; Kuznetsova et al., 2008; Howard and Rubel, 2010). Furthermore, NM receives depolarizing inhibition, which accommodates spike threshold both by recruiting K_LVA and by inactivating sodium channels (Lu and Trussell, 2001; Monsivais and Rubel, 2001; Howard et al., 2007; Fukui et al., 2010). This combination of factors allows NM neurons to function as monaural coincidence detectors, responding maximally to synchronous nVIII inputs while rejecting poorly timed input.

Interestingly, many of these adaptations are tonotopically distributed. Low characteristic frequency (LCF, <500 Hz) neurons have slower membrane kinetics, have high-density Na⁺ channels in the axon initial segment, require smaller currents to spike, and receive many small nVIII inputs, which depress more readily. In contrast, high characteristic frequency (HCF, >2500 Hz) neurons have more rapid membrane kinetics, require much larger currents to spike, and receive only 1 or 2 large, depression-resistant endbulb synapses (Fukui and Ohmori, 2004; Kuba and Ohmori, 2009; Oline and Burger, 2014). The relative and combined contributions of each tonotopically distributed feature to computational output remain unclear.

We approached this broad question first by investigating the influence of single synapses on spike timing across the tonotopic axis in NM. Stimulation of unitary inputs to NM demonstrated that LCF neurons responded with larger latency and jitter than HCF neurons during high stimulation rates. We then assessed NM neurons' subthreshold and superthreshold membrane selectivity for input characteristics. We found that neurons across the tonotopy required different rates of depolarization to evoke responses and that, in HCF neurons, this selectivity shifted dynamically with steady-state voltage. Computational models of LCF, MCF, and HCF neurons assessed how tonotopic selectivity differences affect synaptic integration of phase-locked inputs. All models performed similarly with low-frequency stimuli by integrating multiple subthreshold inputs. However, the HCF model vastly outperformed MCF and LCF models for high-frequency stimuli with fewer inputs. These data reveal mechanistic insights into computational principles that apply broadly to neurons that process temporal information.

Materials and Methods

We recorded 92 NM neurons from 17 white leghorn chicks (Gallus gallus domesticus) age E19-P1 of either sex. Fertilized eggs were obtained from a commercial poultry supplier (Moyer's Chicks) and raised at Lehigh University's central animal facility. All procedures were approved by the Lehigh University Institutional Animal Care and Use Committee and were performed in compliance with the Public Health Service Policy on Human Care and Use of Laboratory Animals.

In vitro brain slice preparation

Acute brain slices were prepared as described by Oline and Burger (2014). Before surgery, embryos were brought to room temperature, and posthatch chicks were anesthetized with isoflurane (MINRAD). Chicks were rapidly decapitated, and the brainstem containing auditory nuclei was removed, blocked, and submerged in oxygenated aCSF containing the following (in mm): 130 NaCl, 3 KCl, 10 glucose, 1.25 NaH₂PO₄, 26 NaHCO₃, 3 CaCl₂, and 1 MgCl₂ at 22°C. The brainstem was placed rostral surface down on the stage of a vibrating microtome (Microm International) to collect 180–200 μm coronal slices, 4–6 of which typically contained the NM. Slices were maintained in topographic order in an incubation chamber of continuously oxygenated aCSF and incubated at 37°C for 45 min, and then maintained at room temperature. The tonotopic position of NM neurons within these coronal slices was estimated according to position along the known rostromedial (high CF) to caudolateral (low CF) axis (Rubel and Parks, 1975; Fukui and Ohmori, 2004). Using the topographic position scheme of the Ohmori group, NM neurons were assigned to 1 of 3 topographically ordered CF subsections (Fukui and Ohmori, 2004). LCF neurons were defined as those within the first (most caudal) slice that contained NM and the lateral third of the second slice. HCF neurons were defined as those within the last slice containing NM and the medial third of the second-to-last slice. All other neurons were defined as middle CF (MCF).

Recording arrangement

Brainstem slices were placed in a custom recording chamber on a retractable chamber shuttle system (Siskiyou), and neurons were visualized with a Nikon FN-1 Physiostation microscope using infrared differential interference contrast optics. Video images were captured using a CCD camera (Hamamatsu) coupled to a video monitor. The recording chamber was continuously superfused with aCSF at a rate of 1.5 ml/min. An inline feedback temperature controller and heated stage were used to maintain chamber temperature at 35 ± 0.50°C (Warner Instruments). Principal NM neurons were identified based on their characteristic round morphology.

Patch pipettes were pulled from thick-walled borosilicate glass capillary tubes (WPI) to a resistance of 3–7 MΩ using a two stage puller (Narishige) and back-filled. We used a potassium-based solution for current-clamp experiments containing the following (in mm): 145 K-gluconate, 5 KCl, 1 MgCl₂, 10 HEPES, and 5 EGTA, pH adjusted to 7.2 with KOH. The signal was digitized with a Digidata 1440 data acquisition board and recorded using Clampex software (Molecular Devices). Membrane voltage was recorded using a Multiclamp 700B amplifier. Junction potentials were measured at 10 mV and adjusted for data analysis. To eliminate responses to spontaneous inhibitory input from the superior olivary nucleus, aCSF included the following: 20 μm SR-95531 hydrobromide, a GABA_A receptor antagonist, and 500 nm strychnine hydrochloride, a glycine receptor antagonist.

Synaptic responses were evoked by electrical stimulation of single auditory nerve inputs, using methods described previously (Dobrunz and Stevens, 1997; Oline and Burger, 2014). Briefly, we positioned a bipolar tungsten stimulating electrode over the tissue surface with a micromanipulator (Siskiyou), in a dorsolateral position proximal to the cell of interest. Single-fiber, “unitary” evoked EPSCs were isolated using a minimum stimulation protocol, such that EPSCs were considered unitary provided that EPSC amplitude was independent of stimulus amplitude (range 5–90 V), EPSC latency and kinetics were consistent, and a reduction in the stimulus amplitude led to a complete loss of the EPSC. Synaptic inputs that did not meet these criteria were discarded.

Current-clamp protocols

Spike threshold in response to a square current (rheobase) was determined as the minimum square current amplitude required to elicit a spike in at least 50% of trials. We then injected current ramps of increasing maximum amplitude. To determine voltage slope threshold, we measured the final trace that evoked a successful spike from each of five trials. We measured the time point of spiking, required to calculate voltage slope threshold, as the point at which voltage slope changed most rapidly, as measured by the peak of the second derivative. Voltage slope threshold was then measured as the average slope of the middle 20%–80% range between ramp onset and spiking.

Chirp stimulus protocols, which are sine waves that increase in frequency linearly from 0 to 250 Hz over 5 s, were generated in MATLAB (The MathWorks) and imported into Clampex 10.2 (Molecular Devices). Current amplitude was adjusted with the gain function to maintain maximal voltage responses near 5 mV. Fourier transforms of both injected current and voltage responses were performed in MATLAB following application of a Hanning window. Impedance was calculated as the quotient of these two values.

Dynamic-clamp protocols

To model the excitatory postsynaptic conductances (EPSGs) of multiple auditory nerve synaptic inputs onto NM neurons, we accessed neurons using whole-cell patch clamp, and then acquired dynamic-clamp recordings (Kullmann et al., 2004) with the G-clamp 2.1.1 software package (Paul H.M. Kullmann and John P. Horn, Department of Neurobiology and Center for the Neural Basis of Cognition, University of Pittsburgh School of Medicine). We performed these experiments in current-clamp mode at 12 kHz with LabView 8.2 software, a PXI-1031 chassis, and a BNC-2110 connector block (National Instruments). Simulated EPSGs had a reversal potential of 0 mV, and kinetics were fit to the shape of empirically observed unitary EPSCs from previous observations (Oline and Burger, 2014), with input conductance (g_EPSG) set to the following equation with time constants τ_rise and τ_fall set to 0.20 and 0.33 ms, respectively, a normalization factor k (−5.4855), and a maximum conductance (G_max) as follows:

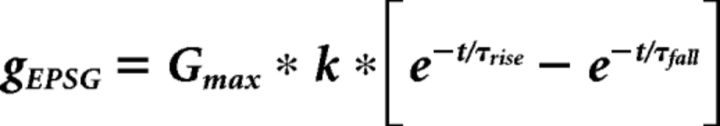We measured spike threshold in response to simulated EPSGs (henceforth referred to as conductance threshold) as the G_max required to initiate spiking in at least 50% of 15 trials. We then evaluated the temporal dynamics of threshold accommodation by pairing a subthreshold input (EPSG₁, G_max set to 70% of conductance threshold) with a second conductance after time t ranging from 0.2 to 5.0 ms (EPSG₂, G_max increased until spikes occurred in at least 50% of trials). In a second experiment, we tested predictions made by our computational model. We simulated multiple synaptic inputs that were phase-locked to a range of stimulus frequencies using the dynamic clamp to inject the same EPSG waveforms that were used in our computational model, described below in Computational modeling: AN input model. Briefly, this 85 s stimulus waveform was the sum of the EPSGs from all modeled auditory nerve synaptic inputs, and an excerpt is represented in Figure 6A, C (synaptic input). To quantify the phase-locked output of spikes from the patched NM neuron resulting from these stimuli, we identified spike times as the peaks of recorded voltage traces after applying a spline interpolation at 120 kHz.

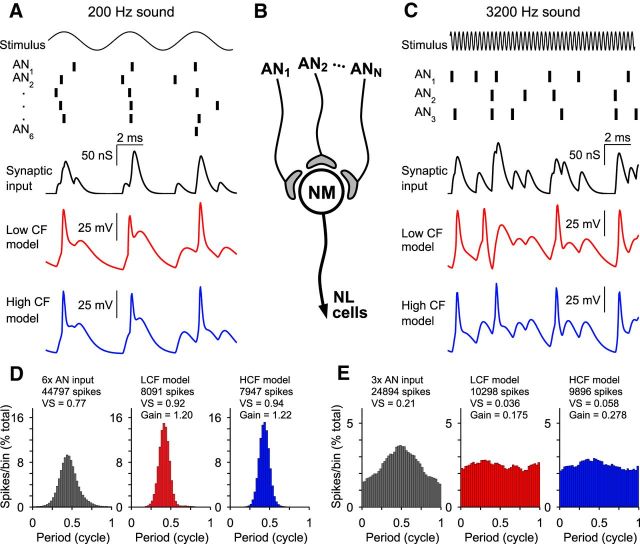
Figure 6.

Model responses to multiple phase-locked inputs. A, C, Model responses to input driven by 200 Hz and 3200 Hz stimuli, respectively. Vertical bars represent timings of inputs phase-locked to the above waveform. Synaptic input to the model is a single conductance, resulting from the summed conductances of many inputs. Responses to identical input by both LCF and HCF models are shown. Spike times are similar for both models responding to 200 Hz input, but that for 3200 Hz input, the HCF model output is less susceptible to summation of input across successive periods. B, Diagram of model synaptic input arrangement. NL, Nucleus laminaris. D, E, Period histograms of spike timing for AN inputs, LCF model, and HCF model after being driven for 40 s. SG is marked for NM model output. The HCF model improves SG to 3200 Hz input relative to the LCF model.

Computational modeling

NM neuron model.

To explore how specialized membrane properties contribute to temporal coding of NM neurons, we constructed a model of NM neurons that receives phase-locked inputs from AN fibers. Table 1 summarizes the model equations, and Table 2 lists CF-dependent parameter values. Our NM model is a single-compartment conductance-based model with leak, K_LVA, and K_HVA conductances. The K_LVA conductance was necessary to reproduce the nonlinear subthreshold dynamics of NM neurons, such as impedance, whereas the K_HVA conductance was adopted to ensure rapid repolarization after spikes. Other active currents, such as I_h (Yamada et al., 2005), are included as constant leak. Slice recording data of our own and others (Fukui and Ohmori, 2004) were used for determining these conductances (Table 2). Kinetics for K_LVA and K_HVA (Table 1) were based on slice recording results by Rathouz and Trussell (1998), after revising the curves to better reproduce our impedance, slope threshold, and dynamic-clamp data.

Table 1.

NM model equations: equations used to simulate NM membrane responses to auditory nerve fiber synaptic input

Variable	Equation
Membrane potential V	$$C\frac{dV}{dt}=I_L+I_{KLVA}+I_{KHVA}+I_{spike}+I_{syn}$$
Leak current	IL = gL(EL − V)
KLVA current	IKLVA = ḡKLVAd(V, t)(EK − V)
KHVA current	IKHVA = ḡKHVAn(V, t)(EK − V)
Spike current	Ispike(t) = A1e(−t/τ1) − A2e(−t/τ2)
Synaptic current	Isyn(t) = gsyn(t)(Esyn − V)
KLVA kinetics	$${\tau }_d\left(V\right)\frac{d}{dt}d\left(V,t\right)=d_{\infty }\left(V\right)-d\left(V,t\right)$$
KLVA time constant	τd(V) = Q10(T − 23)/10/(αd(V) + βd(V))
KLVA steady-state function	d∞(V) = αn(V)/(αn(V) + βn(V))
KLVA activation function	αd(V) = 0.20 e((V + 70)/21.8)
KLVA deactivation function	βd(V) = 0.17 e(−(V + 70)/14.0)
KHVA kinetics	$${\tau }_n\left(V\right)\frac{d}{dt}d\left(V,t\right)=n_{\infty }\left(V\right)-n\left(V,t\right)$$
KHVA time constant	τn(V) = Q10(T − 23)/10/(αd(V) + βd(V))
KHVA steady-state function	n∞(V) = αn(V)/(αn(V) + βn(V))
KHVA activation function	αn(V) = 0.11 e((V + 29)/9.1)
KHVA deactivation function	βn(V) = 0.103 e(−(V + 29)/20.0)
Threshold equation	$${\tau }_{\Theta }\frac{d}{dt}\Theta \left(V,t\right)={\Theta }_{\infty }\left(V\right)-\Theta \left(V,t\right)$$
Target threshold	Θ∞ (V) = Θ0 − KΘ log h∞(V)
Na inactivation function	h∞(V) = 1/(1 + e(V + 65)/7.0)
Unitary synaptic input	gsyn(t) = gunit ∗ kg ∗ (e−t/τR − e−t/τF)

Table 2.

NM model parameters representing LCF, MCF, and HCF neurons

Parameter	LCF model	MCF model	HCF model
Membrane capacitancea C	30 pF	30 pF	30 pF
Leak reversal potentiala EL	−59 mV	−59 mV	−59 mV
K reversal potential EK	−83 mV	−84 mV	−85 mV
Synaptic input reversal potentiala Esyn	0 mV	0 mV	0 mV
Leak conductance gL	4 nS	6 nS	8 nS
KLVA conductance ḡKLVA	4 nS	21 nS	32 nS
KHVA conductance ḡKHVA	32 nS	84 nS	128 nS
Temperature factora Q10	2.0	2.0	2.0
Temperature (in vitro)a T	35°C	35°C	35°C
Temperature (in vivo)a T	40°C	40°C	40°C
Baseline thresholda Θ0	−62 mV	−62 mV	−62 mV
Adaptation factor KΘ	9 mV	10 mV	11 mV
Adaptation time constanta tΘ	0.9 ms	0.9 ms	0.9 ms
Refractory perioda TR	2.0 ms	2.0 ms	2.0 ms
Spike current amplitude A1	55 nA	85 nA	135 nA
Spike current amplitude A2	35 nA	63 nA	110 nA
Spike current time constant τ1	0.12 ms	0.12 ms	0.11 ms
Spike current time constant τ2	0.20 ms	0.17 ms	0.14 ms
Synaptic time constanta τR	0.20 ms	0.20 ms	0.20 ms
Synaptic time constanta τF	0.33 ms	0.33 ms	0.33 ms
Normalization constanta kg	−5.4855	−5.4855	−5.4855

^aCommon to all three CF models.

Similarly to previous modeling work on owl auditory brainstem neurons (Ashida et al., 2015), we introduced a threshold-crossing detector to simulate spiking activity of NM cells. When the membrane potential reaches the threshold Θ at time T_Θ, a spike current I_spike(t − T_Θ) is initiated. We used two exponential functions to simulate the spike shapes of NM neurons (Table 1). Once the threshold is crossed, the threshold-crossing detector is in an absolute refractory period of length T_R, thus no spikes are generated for T_Θ < t < T_Θ + T_R.

To simulate effects of voltage gated sodium channel (Nav) inactivation on spike initiation, we introduced an adaptive threshold to the model (Benda et al., 2010; Platkiewicz and Brette, 2010). Leaky integrate-and-fire models with adaptive thresholds have been used for simulating mammalian (Fontaine et al., 2013) and avian (Fontaine et al., 2014) auditory brainstem neurons. Our threshold equations are summarized in Table 1. In short, the adaptive spike threshold Θ(V,t) approaches the steady-state threshold of Θ_∞(V) with a time constant τ_Θ. Parameters for the threshold adaptation were assumed to be different among LCF, MCF, and HCF neurons and were determined to reproduce results of our dynamic-clamp experiments.

AN input model.

Phase-locked synaptic inputs from AN fibers are modeled as an inhomogeneous Poisson process with a periodic intensity function as follows: λ(t) = 2πλ̄ p_k(2π ft), where t is time, λ̄ is the average intensity, p_k is a 2π-periodic function, and f is the stimulus sound frequency. We used the von Mises distribution function (Fisher, 1993) for the periodic function as follows: p_k(x) = exp(k cos(x))/(2π I₀(k)) with I_n being the modified Bessel function of order n. The degree of phase-locking, measured as vector strength (VS) (Goldberg and Brown, 1969), is related to the concentration parameter k as follows: VS = I₁(k)/I₀(k) (for more detail, see Ashida et al., 2013). We selected concentration parameters so that the VS of simulated AN spikes match previous experimental results (Fukui et al., 2006). We assumed that spiking of all AN fibers were locked to the same phase.

To simulate refractory periods of AN fibers (Avissar et al., 2013), generated spikes that are closer to the preceding spike by T_ref = 1.5 ms were discarded. Because of the refractoriness, simulated spike rates of AN fibers were generally lower than the intensity λ̄. As we are primarily interested in low-intensity stimulation, where inhibitory feedback does not play a major role, we chose values of the input intensity so that simulated AN fibers spike at 180–210 spikes/s. Table 3 summarizes the AN input parameters used for our simulations.

Table 3.

Frequency-dependent auditory nerve model input parameters^a

Sound frequency Hz	200 Hz	400 Hz	800 Hz	1600 Hz	3200 Hz
Input intensity λ̄ (spikes/s)	400	300	300	300	300
Simulated spike rates (spikes/s)	∼185	∼210	∼195	∼205	∼205
Concentration parameter k	2.8713	2.8713	2.8713	1.1593	0.4083
Simulated vector strength	∼0.77	∼0.80	∼0.80	∼0.50	∼0.20

^aParameters used for auditory nerve input to model NM neurons with a range of tested stimulus frequencies.

As in dynamic-clamp experiments, excitatory synaptic inputs from AN to NM were generated using a double exponential function (Table 1). The time constants of this model synaptic input were based on previous slice recordings (Oline and Burger, 2014). In our series of simulations, we varied the number of AN fibers converging onto one model NM neuron from 1 to 16, to compare differences between “a small number of large inputs” and “a large number of small inputs.” Hence, we assumed that the total synaptic input amplitude g_tot is unchanged with the number of inputs. In other words, the unitary synaptic input g_unit was obtained by normalizing the total input g_tot by the number N_in of converging AN fibers as follows: g_unit = g_tot/N_in.

Output measures

To test the plausibility of our NM model, we performed numerical simulations with the same inputs and procedures as we used for our slice recordings. In particular, we calculated impedance properties, integration periods, slope thresholds, and dynamic thresholds. Next, we calculated membrane responses of LCF, MCF, and HCF models using simulated AN inputs. We varied the sound stimulus frequency f, the number of AN inputs N_in, and the total synaptic conductance g_tot to examine how these parameters affect model NM responses.

The output of model NM neurons was examined using the spike rate, the degree of synchrony (in VS), and the average K⁺ current. In all panels, data points with output spike rates of >100 spikes/s are shown. Because the input VS depended on the sound frequency, we normalized output VS by the input VS to obtain a “synchronization gain” (SG). A gain exceeding 1.0 indicates that the NM output has better synchrony than input AN fibers. The average K⁺ current (in pA) was obtained by integrating the K_LVA and K_HVA currents and dividing this total by the simulated time length.

Custom-written MATLAB (The MathWorks) scripts were used for our numerical simulations. With each parameter set, model responses for 40 s (typically with 5000–10,000 spikes) were calculated with a time increment of 5 μs.

Statistics

All data in Results are expressed as percentage of control ± SD. Error bars in figures indicate SE. One-way between groups comparisons were performed using the Kruskal–Wallis H test, one-way repeated measures comparisons were performed using the Friedman test, and two-way between groups comparisons with repeated measures were performed using ANOVA. Effect size of significant results was reported with partial η². When necessary, violations of sphericity were adjusted using the Greenhouse-Geisser correction. Finally, paired-sample between-group comparisons were performed with the Wilcoxon signed-rank test. Data analysis and plotting were performed in MATLAB (The MathWorks), Adobe Illustrator CC (Adobe Systems), and Clampfit (Molecular Devices), and comparisons were calculated in SPSS Statistics (IBM).

Results

Efficacy of unitary synaptic input varies systematically along the tonotopy

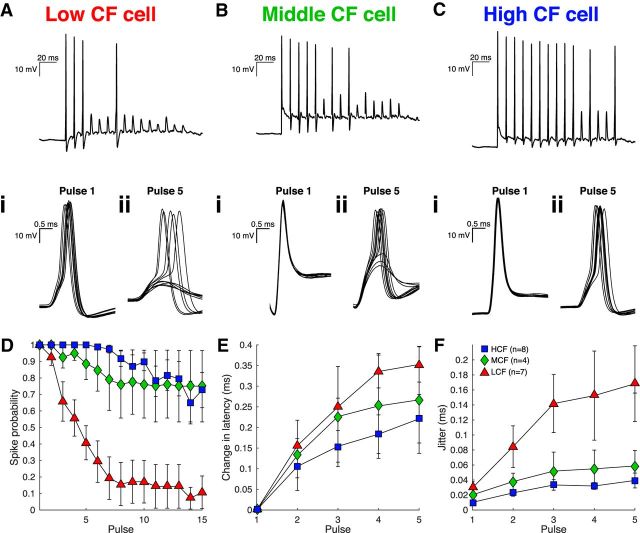
A principal feature of NM response properties is the observed improvement or preservation of phase-locked auditory nerve input (Fukui et al., 2006). Phase-locked NM output is crucial for the binaural neurons in nucleus laminaris, NM's sole postsynaptic target, to compute stimulus position in azimuth (Grothe et al., 2010; Ashida and Carr, 2011). We previously showed that unitary synaptic inputs, which ideally represent single nVIII fibers, are more effective at driving spiking and show less pronounced short-term depression in HCF NM neurons (Oline and Burger, 2014). Here, we extend these findings to evaluate temporal features of the postsynaptic responses using a minimum stimulation paradigm to evoke discharges from unitary inputs in current clamp. Figure 1A–C shows NM neuron responses from three topographically defined regions designated as LCF, MCF, and HCF (see Materials and Methods). Evoked responses from unitary inputs in LCF neurons had larger spike jitter, measured as the SD of spike time in milliseconds, than MCF and HCF neurons, and are consistent with previous observations of responses to stimuli that recruited multiple auditory nerve inputs simultaneously (Fukui and Ohmori, 2004). We additionally observed that NM spike latency and jitter increased systematically in response to repetitive stimulation at 100 Hz, which more closely represents phase-locked synaptic activity during an auditory stimulus. Average latency and spike jitter increased with successive pulses (Fig. 1E,F) (latency, χ₍₄₎² = 68.971, n = 19, p = 0.000001; jitter, χ₍₄₎² = 34.653, n = 19, p = 0.000001, Friedman tests), and jitter within pulses was different between populations (Pulse 5, χ₍₂₎² = 6.777, p = 0.034, Kruskal–Wallis H Test). However, due to the rapidly depressing EPSC amplitude of unitary inputs to LCF neurons, far fewer pulses evoke spikes. Superthreshold inputs presumably represent a subset of stronger EPSCs within the broader distribution of all EPSCs. A consequence of this phenomenon is that, although EPSC amplitude depresses more rapidly in LCF neurons, we did not observe LCF changes in spike latency and jitter to be statistically distinct from MCF or HCF cells (latency, F_(2.78,22.20) = 1.13, n = 19, p = 0.36; jitter, F_(3.95,31.58) = 1.77, n = 19, p = 0.16, 3 × 5 mixed repeated-measures ANOVAs). Although the tonotopic distribution of short-term synaptic depression may account for a portion of these effects in spike timing (Oline and Burger, 2014), tonotopic differences in postsynaptic membrane excitability may also affect spike timing. We therefore investigated the postsynaptic membrane's possible contribution to synaptic integration and, importantly, phase-locking precision.

Figure 1.

Efficacy of unitary synaptic input varies systematically along the tonotopy. A–C, Evoked responses to stimulation of unitary auditory nerve fibers at 100 Hz for LCF (triangles), MCF (diamonds), and HCF (squares) neurons. Insets, Comparison of spike timing between Pulse 1 (i) and Pulse 5 (ii) for each neuron. D, Spike probability for 15 pulses at 100 Hz over 10 trials. E, Mean change in latency relative to Pulse 1 for Pulses 1–5. F, Mean spike time jitter for Pulses 1–5.

Membrane impedance in NM neurons is dependent on both CF and steady-state potential

The magnitude and kinetics of a neuron's response to synaptic input are dependent on membrane impedance, whereby low impedance speeds voltage responses but attenuates response magnitude. To explore the membrane's filter properties in the subthreshold domain and to assess input selectivity at rest, we used a chirp protocol (also known as a ZAP) in current-clamp mode. Chirp stimuli efficiently probe membrane responses over a broad range of frequencies through injection of frequency-modulated sinusoidal current sweeps from 0 to 250 Hz (Hudspeth, 1985; Hutcheon and Yarom, 2000). We adjusted chirp amplitude so that the maximum membrane voltage response was 5 mV peak to peak. Peak impedance frequency (f_R) was then measured as the frequency of current injection that resulted in the largest voltage deflection.

Passive neural membranes, which can be electrically modeled with a resistor and capacitor in parallel, have predictable low pass responses to broadband input. Chirp stimulus current injections into NM neurons indeed evoked voltage responses that resemble low pass filter properties, whereby slowly fluctuating inputs result in large voltage deflections, and higher-frequency inputs are attenuated. For an ideal passive neuron membrane model, impedance would be maximal at zero frequency. However, in real neurons, slow depolarization evoked by low-frequency input rapidly recruits active voltage-gated conductances, such as those mediating low-threshold potassium current (K_LVA). This outward conductance has been shown to activate in NM between −75 and −65 mV (Reyes et al., 1994; Rathouz and Trussell, 1998; Fukui and Ohmori, 2004). Therefore, we predicted that HCF and MCF neurons, which have large K_LVA, would preferentially attenuate responses to low-frequency input compared with LCF neurons. Rather, we observed that f_R and maximum impedance for resting neurons were not different across the tonotopy (LCF: 11.1 ± 7.19 Hz, n = 14; MCF: 19.1 ± 18.91 Hz, n = 16; HCF: 25.16 ± 62.28 Hz, n = 15; χ₍₂₎² = 1.280, p = 0.527; LCF: 166.4 ± 40.4 MΩ; MCF: 148.1 ± 147.8 MΩ; HCF: 138.3 ± 91.4 MΩ; χ₍₂₎² = 3.926; p = 0.140, Kruskal–Wallis H Tests). This was true despite a tonotopic distribution of resting membrane potential (LCF: −64.86 ± 2.85 mV; MCF: −70.69 ± 3.74 mV; HCF: −72.67 ± 4.15 mV, χ₍₂₎² = 20.007, p = 0.000045, Kruskal–Wallis H Test), as observed previously (Fukui and Ohmori, 2004). Sample traces of LCF (Fig. 2A) and HCF (Fig. 2B) neurons exhibit similar responses at rest. These data suggest that, even though K_LVA is enriched in HCF neurons, hyperpolarization of the resting membrane potential driven by high K_LVA expression maintains this conductance at minimal activation near rest. The contribution of tonotopically distributed K_LVA to spike timing may therefore only arise when the membrane is depolarized.

Figure 2.

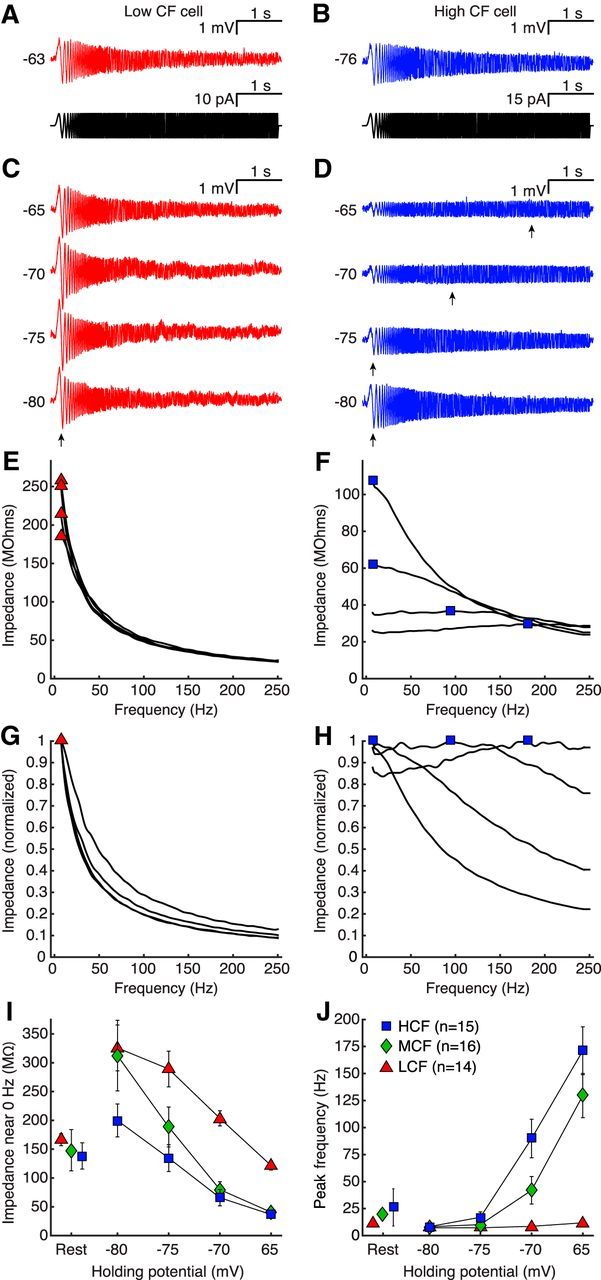
Membrane impedance in NM neurons is dependent on both CF and steady-state potential. A, B, Membrane voltage in response to chirp current injection (insets) for LCF and HCF representative cells. C, D, Membrane voltage of cells in A, B, after adjusting holding voltage (V_H) with slow current in 5 mV steps from −80 to −65 mV. Voltage deflection to slow input and peak impedance frequency (f_R) is stable for the LCF cell but attenuates and shifts, respectively, for the HCF cell (arrows). E, F, Impedance profiles for traces in C, D, with f_R marked for LCF (triangles) and HCF (squares) samples. G, H, Normalized impedance profiles for C, D, demonstrating a large shift in HCF selectivity from slow to fast input. I, Impedance near 0 Hz for LCF (triangles), MCF (diamonds), and HCF (squares) populations at rest (left) and at adjusted V_H (right). Depolarizing membrane potentials reduced impedance for all CF populations, and the magnitude was dependent on population. J, f_R for LCF, MCF, and HCF populations at rest (left) and at adjusted membrane potentials (right). LCF f_R remains stable in all conditions, whereas MCF and HCF f_R shift with depolarization.

We manipulated K_LVA activation by setting membrane voltage to specific values using a steady current injection to achieve 5 mV increments over a 15 mV range from −80 to −65 mV, encompassing most of the K_LVA activation range (Fig. 2C,D). Then we presented chirp protocols at these varied “resting” voltages. At a holding voltage (V_H) of −80 mV, all neurons exhibited low-pass characteristics, with f_R near 0 Hz (arrows), similar to the results at V_rest. However, as we adjusted V_H to more positive potentials, voltage output to the slowest part of the chip stimulus was significantly attenuated (Fig. 2E,F) (LCF: χ₍₃₎² = 29.400, p = 0.000002; MCF: χ₍₃₎² = 48.000, p = 0.000001; HCF: χ₍₃₎² = 45.000, p = 0.000001, Friedman tests). In MCF and HCF neurons, this attenuation of responses to slow input was so prominent that the filter envelope altered from low-pass to all pass (LCF: χ₍₃₎² = 8.818, p = 0.032; MCF: χ₍₃₎² = 41.107, p = 0.000001; HCF: χ₍₃₎² = 38.419, p = 0.000001, Friedman tests) (Fig. 2D). Although the response envelope in MCF and HCF neurons suggests a lack of frequency selectivity at depolarized values, there was a measurable and systematic shift in peak impedance frequency, which is observed in normalized impedance functions (Fig. 2G,H,J) (F_(2.84,59.54) = 19.42, p = 0.000001, η² = 0.48, 3 × 4 mixed repeated-measures ANOVA). This shifting phenomenon indicates that the mechanism underlying the envelope change did not saturate over the −80 to −65 mV range of resting voltages (Fig. 2J), consistent with the putative K_LVA activation range. Together, these data suggest that the response properties of NM neurons are specific to tonotopic position. LCF neurons respond maximally to slow, DC-like input, whereas MCF and HCF neurons dynamically adjust their responses conditionally, selecting for faster input when depolarized. Although these responses to chirp protocols reflect the membrane's adaptive input selectivity, it remains unclear whether threshold criteria for spiking are also adaptive. We therefore next asked whether tonotopic position affected the integration period preceding a spike.

Integration period and slope threshold of NM neurons are tonotopically distributed

The long stimulus periods encountered by low CF neurons may provide sufficient summation time for temporally jittered synaptic inputs without disruption of spike generation. In contrast, the short stimulus period at high frequencies constrains integration time for HCF neurons. Our observation that a neuron's CF is predictive of filtering properties suggests that NM neurons may prefer synaptic input with characteristics that vary with tonotopic position. It is important to consider that K_LVA and axonal sodium channels (Nav), which are both tonotopically distributed in NM, affect response properties in a number of ways (Fukui and Ohmori, 2004; Kuba and Ohmori, 2009). First, K_LVA lowers the input resistance of a cell, speeding EPSP kinetics and attenuating amplitude. This property was manifested most obviously by differences in action potential threshold to 100 ms square current injections (LCF: 281.1 ± 91.2 pA; MCF: 687.5 ± 324.8 pA; HCF: 980.0 ± 436.2 pA, χ₍₂₎² = 22.769, p = 0.000011, Kruskal–Wallis H Test), confirming previous observations (Fukui and Ohmori, 2004). Second, the latency in K_LVA activation puts a lower limit on the rate of depolarization that will initiate a spike because any currents that depolarize the membrane more slowly than that limit become shunted by K_LVA. Third, prolonged depolarization accommodates spike threshold through Nav inactivation (Monsivais and Rubel, 2001; Svirskis et al., 2004). To test whether HCF cell membranes require faster depolarization, we used a current ramp protocol to evoke depolarizing membrane potentials at varying rates (Ferragamo and Oertel, 2002; McGinley and Oertel, 2006; Kuba and Ohmori, 2009) (Fig. 3A,B, same sample cells as in Fig. 2). Spike initiation, the point where voltage slope changed most rapidly, was measured as the peak of the voltage's second derivative, and we defined integration period as the latency from onset to spike initiation (Fig. 3A,B, brackets). We then defined slope threshold as the voltage slope preceding a spike (middle 20%–80%). For each of five trials, the sweep with the most shallow ramp depolarization slope was defined as “slope threshold.”

Figure 3.

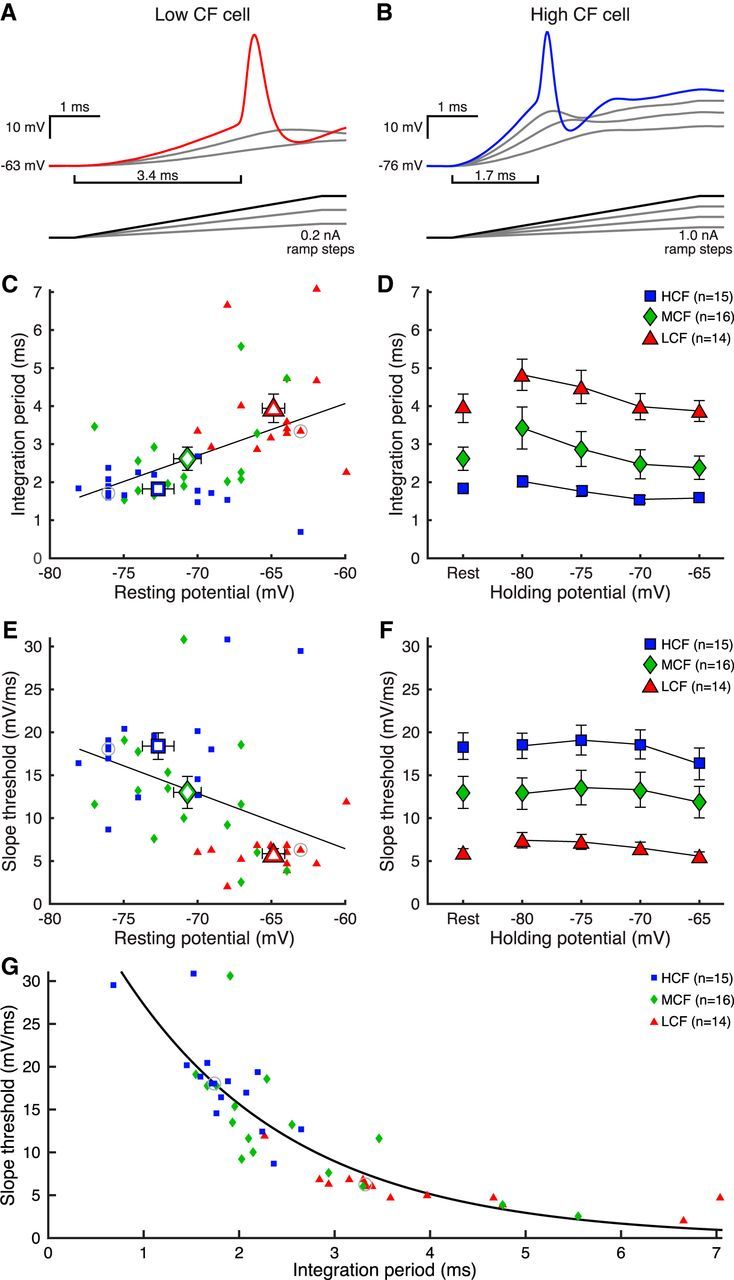
Integration period and slope threshold of NM neurons are tonotopically distributed. A, B, Membrane voltage in response to ramp current injection (insets) for LCF and HCF representative cells. Brackets represent duration of integration period. C, Resting membrane potential versus integration period for LCF (triangles), MCF (diamonds), and HCF (squares) cells. Data are fitted with a least-squares regression. White-filled centroids represent means for each population. Gray circles represent cells in A, B. D, Integration period data of cells at rest in C (left) and at adjusted V_H (right). Integration period was shortest for HCF cells and narrowed with depolarized V_H for all populations. E, Resting membrane potential versus voltage slope threshold for LCF, MCF, and HCF cells. Data are fitted with a least-squares regression. White-filled centroids represent means for each population. Gray circles represent cells in A, B. F, Slope threshold data of cells at rest in E (left), and at adjusted V_H (right). Slope threshold was steepest for HCF cells, and V_H-dependent changes were minimal and not systematic. G, Integration period versus slope threshold for data in C, E, fit with a single exponential curve. Gray circles represent cells in A, B.

We found that both integration period and slope threshold followed the tonotopic gradient. Integration period was longest for LCF cells (Fig. 3C) (LCF: 1.82 ± 0.46 ms, n = 14; MCF: 2.62 ± 1.14 ms, n = 16; HCF: 3.94 ± 1.40 ms, n = 15; χ₍₂₎² = 22.542, p = 0.000013, Kruskal–Wallis H Test) and was positively correlated with resting potential (r = 0.49, p = 0.00069, Pearson correlation). Additionally, LCF cells had the shallowest slope threshold (Fig. 3E) (LCF: 5.86 ± 2.18 mV/ms, n = 14; MCF: 13.00 ± 7.00 mV/ms, n = 16; HCF: 18.39 ± 5.80 mV/ms, n = 15; χ₍₂₎² = 23.626, p = 0.000007, Kruskal–Wallis H Test), which was negatively correlated with resting potential (r = −0.42, p = 0.0039, Pearson correlation). Considering the previous observation that membrane filter properties depend on membrane voltage, we found complementary effects on integration period during ramp stimuli, specifically that integration period decreased with depolarized V_H for all populations (Fig. 3D) (LCF: χ₍₃₎² = 23.460, p = 0.000032; MCF: χ₍₃₎² = 33.150, p = 0.000001; HCF: χ₍₃₎² = 25.640, p = 0.000011; Friedman tests). This nonsystematic effect can be observed in Figure 3F (LCF: χ₍₃₎² = 25.543, p = 0.00012; MCF: χ₍₃₎² = 8.625, p = 0.0347; HCF: χ₍₃₎² = 15.80, p = 0.00125; Friedman tests), with post hoc effects only at the most depolarized conditions. For clarity, the integration period and slope threshold of each cell at rest are presented together in Figure 3G, are highly inversely correlated (R² = 0.76), and are well described by the single exponential fit, y = 47.58 * e^−x/1.798. Because this was performed in the same cells as in Figure 2, we could then ask whether a cell's dynamic range of f_R across V_H predicts either the cell's integration period or slope threshold. We calculated f_R range as the difference in values between the −80 and −65 mV conditions, and found that a broad frequency response range predicts a narrow integration period and a steep slope threshold (integration period r = −0.57, p = 0.000051, slope threshold r = 0.44, p = 0.0024, Pearson correlations). T, responses to chirp, and ramp protocols suggest that neurons in NM have filter functions that depend on tonotopic position and are strong predictors of integration properties for spike timing. If these inherent membrane properties do modulate input-output functions, it is important to test this hypothesis with naturalistic synaptic-like inputs. We therefore used dynamic clamp to probe integration during subthreshold input.

Dynamic input threshold is more selective for HCF NM neurons

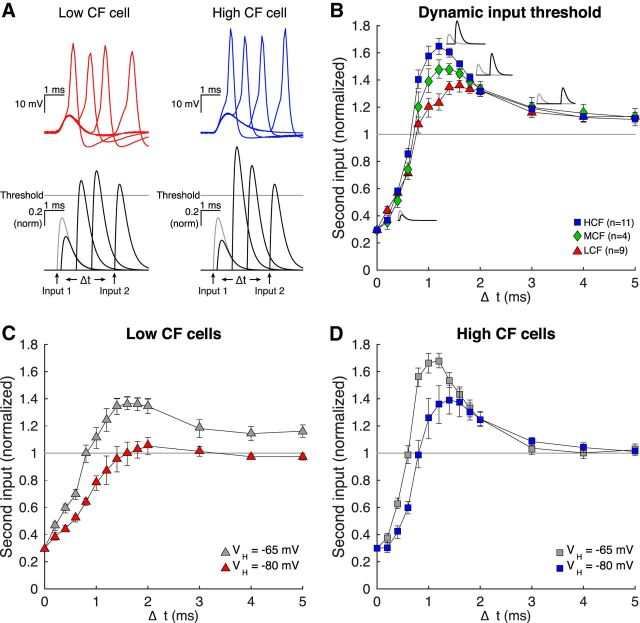
NM membrane responses to both chirp and ramp current injections demonstrate that HCF neurons reject slow input more strongly than LCF neurons. The voltage dependence of this property suggests that this selectivity is primarily regulated by the known, tonotopically distributed K_LVA gradient. Although artificial inputs, such as chirps and ramps, reveal differences in membrane filter properties, they do not provide clear predictions for how the membrane would integrate temporally distributed synaptic input. It is important to consider that K_LVA activation would follow depolarization from subthreshold synaptic input, creating a limited window of time when a second input could initiate spiking. Indeed, strong spike threshold accommodation has been observed in NM neurons following subthreshold input (Howard and Rubel, 2010). In this way, NM neurons are thought to function as monaural coincidence detectors by spiking only in response to closely timed synaptic events. To assess temporal and threshold constraints on realistic synaptic inputs, we injected synaptic-like conductances in dynamic clamp (Robinson and Kawai, 1993; Sharp et al., 1993) and evaluated shifts in spike threshold in each CF domain. EPSGs were modeled as double exponential waveforms and were fit to EPSC records from previously published voltage-clamp data (Oline and Burger, 2014). We defined conductance threshold as the amplitude of the modeled EPSG required to generate a spike in >50% of trials. As expected, unitary conductance threshold, the conductance magnitude required to trigger a spike, was larger for HCF neurons (LCF: 14.86 ± 2.98 nS, n = 9; MCF: 16.91 ± 2.23 nS, n = 4; HCF: 24.18 ± 3.63 nS, n = 11, χ₍₂₎² = 15.849, p = 0.000362, Kruskal–Wallis H Test). We then investigated the temporal dynamics of spike threshold accommodation with a protocol adapted from Howard and Rubel (2010). First, we injected a subthreshold input set at 70% of unitary conductance threshold (EPSG₁). At “synaptic input” intervals ranging from 0.2 to 5 ms, we applied a second, variable amplitude conductance (EPSG₂) until threshold magnitude was reached. This second input magnitude was then defined as the conductance threshold (Fig. 4A). In the absence of K_LVA activation and Nav inactivation, we would expect EPSG₂ threshold at t = 0 to sum with EPSG₁ (fixed at 70% unitary threshold) to be 30% of unitary threshold, and to asymptote to 100% over longer intervals as EPSG₁ decays. However, depolarization from EPSG₁ activates K_LVA in a way that lags membrane depolarization, such that subsequent inward currents are shunted and EPSG₁ + EPSG₂ must sum to greater than unitary conductance threshold to drive a spike. Second, the initial subthreshold EPSG₁ event also confers Nav inactivation, which also contributes to increased threshold. Put simply, EPSG₁ causes EPSG₂ threshold to overshoot unitary conductance threshold; and for this period of time, the neuron is refractory. Considering the known gradient in K_LVA and Nav along the tonotopic axis of NM, we predicted that HCF neurons would exhibit more accommodation and that its peak would occur with shorter latency. Indeed, HCF neurons had a more dynamic spike threshold (Fig. 4B) (3 × 14 mixed repeated-measures ANOVA, F_(3.77,32.02) = 3.91, p = 0.012, η² = 0.32) with a larger and earlier peak than MCF or LCF neurons.

Figure 4.

Dynamic input threshold is more selective for HCF NM neurons. A, Membrane voltage in response to conductance clamp injection (insets) for LCF and HCF representative cells. Threshold (gray line) was measured for a unitary synaptic conductance based on empirical recordings of synaptic input and delivered in dynamic clamp. Dynamic input threshold was measured by injecting an input at 70% threshold (Input 1, gray trace), then injecting a second input (Input 2, black trace) following a delay of Δt, and increasing the magnitude of Input 2 until spiking occurred in >50% of trials. Threshold Input 2 magnitude is depicted for several delays. B, Dynamic input threshold for LCF (triangles), MCF (diamonds), and HCF (squares) cells. Value at time 0 is mathematically determined to be 30%, and threshold was measured for Input 2 at Δt from 0.2 to 5.0 ms. Insets, Conductance waveform that elicited a spike at various Δt. C, D, Dynamic input threshold for LCF and HCF cells, respectively; V_H at of −80 (red/blue) and −65 (gray) mV. Depolarized V_H induces a more selective dynamic threshold for both populations.

We then asked how depolarization constrained temporal integration by adjusting holding voltage for each cell to −65 mV and −80 mV, and observed V_H-dependent-changes in spike threshold accommodation for both LCF (Fig. 4C) and HCF (Fig. 4D) populations (LCF: F_(2.30,23.04) = 4.45, n = 6, p = 0.019, η² = 0.0302; MCF: F_(1.47,5.88) = 0.78, n = 3, p = 0.46; HCF: F_(2.06,20.55) = 5.99, n = 6, p = 0.085, η² = 0.375, 2 × 14 mixed repeated-measures ANOVAs), demonstrating that depolarization restricts temporal integration. Interestingly, unitary conductance threshold was only different between V_H conditions for LCF neurons (LCF: 14.28 ± 2.56 nS at −65 mV and 20.57 ± 3.86 nS at −80 mV, n = 6, Z = −2.201, p = 0.028; MCF: 15.52 ± 2.16 nS at −65 mV and 19.10 ± 7.77 nS at −80 mV, n = 3, Z = −1.069, p = 0.285; HCF: 24.21 ± 2.52 nS at −65 mV, 27.46 ± 6.01 nS at −80 mV, n = 6, Z = −1.153, p = 0.25, Wilcoxon signed-rank tests), suggesting that while depolarization may bring all neurons closer to voltage threshold, the conductance requirements to initiate a spike remain unchanged for HCF and MCF neurons.

Computational modeling demonstrates distinct integration strategies

To understand whether these tonotopic membrane response properties of NM neurons confer specific strategies for synaptic integration, we next devised computational models of LCF, MCF, and HCF neurons. These single-compartment models contained leak, K_LVA, and K_HVA conductances, and a spike current with an adaptive threshold (Table 1). Parameters were adjusted for models (Table 2) so that model response properties reflected those from our slice physiology recordings (Fig. 5). Injection of chirp currents to the models resulted in membrane potentials that, like our observed recordings, shifted from low-pass to all-pass depending on V_H, with tonotopically dependent dynamic ranges (Fig. 5A–C). The model neurons also responded similarly to ramp current injection, whereby the integration period was more prolonged for the LCF model (Fig. 5D–F). Finally, when we provided asynchronous synaptic-like inputs to the models, EPSG₂ threshold increased rapidly and then returned to baseline. The peak of the dynamic threshold occurred earliest and strongest for the HCF model (Fig. 5G–I). V_H-dependent shifts in conductance threshold were also consistent with the physiological results shown in Figure 4C, D for LCF and HCF neurons, respectively (Fig. 5J,K).

Figure 5.

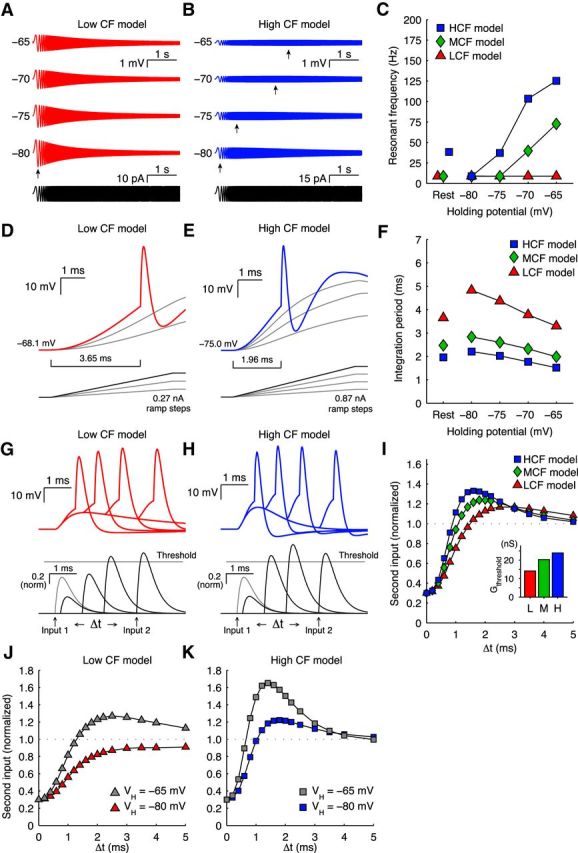
Responses of computational models to input. A, B, LCF and HCF model responses to chirp current injection (0–250 Hz) with changing V_H. C, Peak impedance (f_R) for LCF (triangles), MCF (diamonds), and HCF (squares) models to chirp current injection. D, E, LCF and HCF model responses to ramp current injection. F, Integration period for LCF (triangles), MCF (diamonds), and HCF (squares) models to chirp current injection. G, H, LCF and HCF model responses to paired, asynchronous conductances. I, Dynamic spike threshold for LCF (triangles), MCF (diamonds), and HCF (squares) models to paired, asynchronous conductances. Inset, Unitary conductance thresholds. J, K, LCF and HCF model dynamic spike threshold at V_H of −65 mV and −80 mV demonstrates a dependence on membrane potential that is similar to physiological data (Fig. 4C, D).

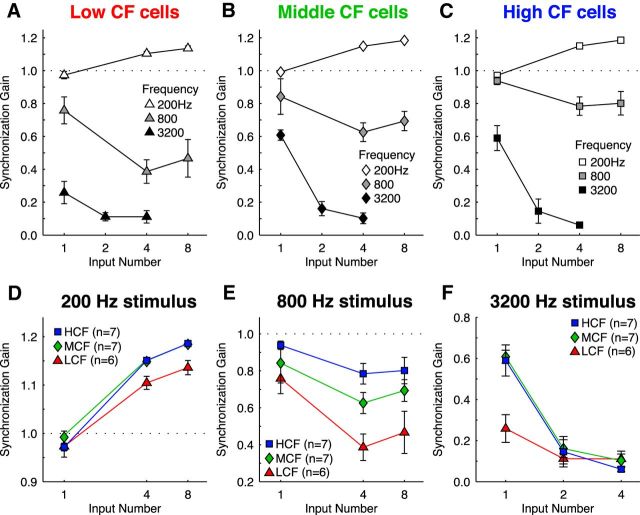
To investigate how the number and size of converging synaptic inputs interact with membrane response properties to adjust phase-locking, we then provided simulated synaptic inputs to these models (Fig. 6). We varied the number of model auditory nerve inputs from 1 to 16 while keeping total conductance fixed (Fig. 6B), so that we tested a range from many small inputs to a few large inputs. In a separate simulation (data not shown), we fixed unitary input amplitude and allowed total conductance to change. Results with these input characteristics were not qualitatively different; therefore, we did not further pursue this paradigm. Representative conditions are presented, including 200 Hz and 3200 Hz stimuli evoking inputs to both LCF and HCF models (Fig. 6A,C). Spike rate and jitter of phase-locked inputs were based on responses to pure tones from in vivo auditory nerve recordings (Fukui et al., 2006). We used our recordings from unitary synaptic responses in NM to model input kinetics (Oline and Burger, 2014). These inputs evoked phase-locked output spikes in the model neurons, which we compared with the temporal precision present in input spike trains using period histograms (Fig. 6D,E). We measured phase-locking using vector strength, where a value of 0 represents no relationship between stimulus phase and spike timing and a value of 1 represents perfect phasic synchrony (Goldberg and Brown, 1969). We then quantified the NM neuron's effect on phase-locking using SG, the ratio of output vector strength and input vector strength. Synchronization gain values >1 represent improvement in vector strength, whereas values <1 represent a degradation of phase-locking. Six inputs enhanced vector strength for a 200 Hz stimulus by ∼20% (SG = 1.20–1.22), whereas 3 inputs eliminated almost all phase information for a 3200 Hz stimulus (SG = 0.18–0.28) for both LCF and HCF models.

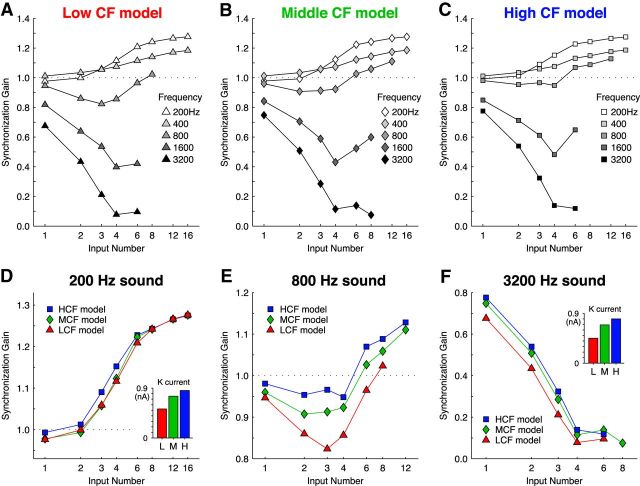
We then measured synchronization gain for a range of input number and stimulus frequency combinations (Fig. 7). All models showed synchronization gain improvements for 200 Hz stimuli with an increasing input number, but with diminishing return per input above 8 inputs (Fig. 7A–C, white symbols). Additionally, the stimulus frequency where the optimal number of inputs switched from many inputs to few was near 800 Hz, where synchronization gain was essentially flat regardless of input number. Synchronization gain for stimulus frequencies ≥1600 Hz in all models was <1 and best for just a single input, suggesting that stimulus periods were too short for the model neuron to benefit from temporal summation of multiple inputs, as implied by the dynamic-clamp data in Figure 4.

Figure 7.

Synchronization gain of computational models to a range of stimulus parameters. A–C, Responses of the LCF (triangles), MCF (diamonds), and HCF (squares) models to simulated phase-locked auditory nerve input across a range of stimulus frequencies and input number. All neuron models responded best to low stimulus frequencies with many inputs, and to high stimulus frequencies with a single input. D–F, Responses from A–C separated by stimulus frequency, expanded ordinate. D, Responses to 200 Hz input showed benefits with many inputs, but little difference between computational models. Inset, Average K⁺ current for 16 inputs. E, Responses to 800 Hz input showed relatively invariant SG with input number, with SG increases occurring only at very large input numbers, and with MCF and HCF models. F, Responses to 3200 Hz input showed highest SG for only a single input, and SG increases in the MCF and HCF models. Inset, Average K⁺ current for 1 input. A–F, Data points with output spike rates of >100 spikes/s are shown, to reflect only responses above the criterion-predicted spontaneous rate established by previous physiological studies (Warchol and Dallos, 1990; Fukui et al., 2006).

To assess the postsynaptic membrane's contribution to phase-locking, we then compared the responses of each model to 200, 800, and 3200 Hz stimuli (Fig. 7D–F). When driven by a 200 Hz stimulus, all model cells responded with remarkably similar synchronization gain, meaning that no advantage is conferred by response characteristics that are specific to CF (Fig. 7D). However, higher stimulus frequencies quickly revealed membrane-dependent differences in phase-locking. The LCF model performed substantially worse than the MCF and HCF models in response to the 800 Hz stimulus (Fig. 7E), and the apparent recovery of SG for LCF neurons at 6–8 inputs is accompanied by a steep fall in response rate (data not shown). Finally, in the 3200 Hz stimulus condition, responses were temporally dispersed relative to auditory nerve inputs in all models, but the HCF model output preserved the most phase information (Fig. 7F). Potassium current was also measured during activity and was largest in the HCF model (Fig. 7D,F, insets). In summary, the models predict that the ideal arrangement of synaptic convergence and membrane properties is specific to stimulus frequency and that a fast membrane time constant is most beneficial when representing high-frequency stimuli with a single input.

Synchronization gain of real NM neurons to a range of stimulus parameters

We then sought to test the predictions derived from our computational model in vitro using identical input timing and conductance waveforms. We simulated 1–8 synaptic inputs to NM neurons in each CF area with dynamic clamp (Fig. 8). Neurons were driven for 80 s with inputs phase-locked to 200, 800, and 3200 Hz stimuli, yielding several thousand spikes per trial. The empirically observed synchronization gain patterns were very similar to model predictions. Neurons responded best to 200 Hz stimuli with increasing input number (χ₍₂₎² = 40.0, n = 20, p = 0.000001, Friedman test), and best to 3200 Hz stimuli with only a single large input (χ₍₂₎² = 22.3, n = 20, p = 0.000014, Friedman test). In contrast, input number affected synchronization gain of responses to 800 Hz in a nonmonotonic manner (χ₍₂₎² = 20.8, n = 20, p = 0.000030, Friedman test). Between populations, HCF and MCF cells responded with statistically higher synchronization gain than LCF cells for 3200 Hz stimuli (F_(3.83,32.51) = 6.91, n = 20, p = 0.00045, η² = 0.45, mixed repeated-measures ANOVA). While LCF neurons appeared to have a lower synchronization gain at 200 Hz with 8 inputs than MCF and HCF neurons, the difference was not significant (F_(2.10,17.84) = 1.899, n = 20, p = 0.13, 3 × 3 mixed repeated-measures ANOVA). The difference between model predictions and this trend may be because the model operates at a higher temperature (40°C compared with slice recordings at 35°C) or because it has no noise sources, whereas real neurons have a variety of stochastic processes, such as channel noise. Overall, the outcomes of our computational model and in vitro recordings reveal computational advantages for fewer inputs and a more selective postsynaptic membrane as stimulus frequency increases.

Figure 8.

Synchronization gain of real NM neurons to a range of stimulus parameters. A–C, Responses of LCF, MCF, and HCF neurons to simulated auditory nerve input responding to a range of stimulus frequencies and input number. All neurons responded best to low stimulus frequencies with many inputs, and to high stimulus frequencies with a single input. D–F, Responses from A–C separated by stimulus frequency, expanded ordinate. D, Responses to 200 Hz input showed benefits with many inputs, but little difference between neurons from different tonotopic positions. E, Responses to 800 Hz input showed relatively invariant SG with increasing input number, and increased SG for MCF and HCF neurons. F, Responses to 3200 Hz input showed highest SG for only a single input, and increased SG for MCF and HCF neurons.

Discussion

In this report, we observed that unitary auditory nerve fibers drive responses in NM with systematic increases of spike latency and jitter under repetitive stimulation at physiological rates. We then demonstrated that the membrane contributes to these response patterns in several important ways. First, we showed that membrane selectivity for input features is tonotopically distributed. LCF neurons have stable, low-pass response properties with long integration periods, whereas HCF neurons strongly attenuate slow inputs when depolarized, resulting in a very short integration period. Using naturalistic EPSGs with dynamic clamp, we empirically defined the physiological constraints on temporal integration, showing that, following a subthreshold input, a depolarized HCF neuron rejects a second, asynchronous input more strongly than MCF or LCF neurons. Together, these data suggest that along NM's tonotopic gradient, asynchronous input can readily sum to threshold in LCF neurons but is progressively more strongly rejected by MCF and HCF neurons. We then probed the effect of input number on synaptic integration in each tonotopically defined category using computational models, which made two key predictions: (1) the optimal input number depends on stimulus frequency alone; and (2) the benefits accrued to the HCF model by a short integration period and enhanced spike threshold adaptation only provided a computational advantage when inputs were driven at high frequencies. Finally, dynamic-clamp recordings confirmed that tonotopically distributed membrane properties in NM confer advantages for synaptic integration that are specific to stimulus frequency. These data suggest that a low input resistance and an accommodating voltage threshold improve phase-locking by preventing summation of synaptic inputs across multiple stimulus periods for representation of high-frequency stimuli.

Neurons responding to converging phase-locked synaptic inputs must perform two tasks: integrate stimulus-driven inputs to improve phase-locked output, and simultaneously prevent summation across stimulus periods (Rothman et al., 1993). At low stimulus frequencies, the synaptic integration window is relatively unconstrained by period length, and phase-locking is improved through summation of converging, subthreshold inputs. At high stimulus frequencies, however, the brief stimulus period encroaches upon the integration window, imposing a strict cutoff between the computational benefit of summation and the costs of responding to jittered inputs. We showed that MCF and HCF neurons are competent to dynamically adapt their integration window in response to input, whereby depolarization shifted membrane selectivity toward faster depolarization and more coincident input (Figs. 2–4). At the very highest stimulus frequencies, where stimulus period is shorter than the integration window in even the lowest impedance HCF neurons (3200 Hz, 0.31 ms), distinguishing between inputs that are responding to sequential periods becomes impossible. Indeed, even when neurons received large numbers of inputs, the probability that a high-frequency stimulus would evoke two or more inputs within a single period was small. Instead, inputs dispersed over multiple periods, resulting in a depolarization block and response failure (Fig. 5C). For these reasons, the temporal characteristics of high-frequency stimuli are best maintained with fewer but stronger inputs, a classic “relay-like” arrangement.

Anatomical and physiological observations of the chick auditory brainstem directly support the conclusions that optimal synaptic convergence for phase-locking is dependent on stimulus frequency and that a selective postsynaptic membrane confers a stronger computational advantage only for higher stimulus frequencies. In the chicken, LCF neurons receive >8 subthreshold inputs and have relatively low input thresholds, whereas HCF neurons receive few (∼1–2) superthreshold endbulb synapses and are less excitable (Fukui and Ohmori, 2004). The previous observation that inputs to LCF neurons show pronounced short-term synaptic depression would magnify this optimal tonotopic gradient in input magnitude (Oline and Burger, 2014). Additionally, in vivo recordings in NM have shown that LCF neurons phase-lock more precisely than their auditory nerve inputs up to stimulus frequencies of ∼800 Hz, whereas HCF neurons actually show less temporally precise output than their inputs (Fukui et al., 2006).

In the context of functional homogeneity within NM, where all neurons provide phase-locked discharges to binaural coincidence detectors, we demonstrate that their computational strategy ranges from an integrate-and-fire summation to a simple relay in accordance with constraints imposed by stimulus frequency. For example, the very fast time constant of HCF cells obviates dendrites in the HCF region, even if a dendrite could otherwise average the arrival time of many inputs phase-locked to a high-frequency stimulus. This may explain why dendrites have only been observed for NM neurons in the LCF region, akin to the frequency-dependent dendrite length gradient in NL (Smith and Rubel, 1979; Deitch and Rubel, 1989; Agmon-Snir et al., 1998). Additionally, the large K_LVA conductances necessary for the dynamic membrane properties also incur metabolic costs because approximately half of the energy consumption of a neuron is associated with Na⁺/K⁺-pump activity (Ames, 2000; Laughlin, 2001). The cumulative cost of maintaining temporal precision with high K⁺ conductances may explain why MCF neurons have higher input resistance than their HCF counterparts, even though our experiments show increased synchronization gain for HCF cells when responding to mid-range 800 Hz stimuli.

At higher stimulus frequencies, integration of converging subthreshold inputs would only be beneficial if the integration window is shorter than the stimulus period. Therefore, our observation that depolarization shortened integration periods and required more synchronous subthreshold input led us to predict that, under certain input conditions, neurons would switch from relaying a single input to integrating multiple subthreshold inputs. When we presented neurons with phase-locked inputs, we saw little evidence of such a “mode switch.” Rather, high-frequency stimuli were always best represented with a single input. This may be because the rise in the membrane's dynamic threshold was coupled to a narrowing of the integration window for shorter stimulus periods, rendering coincident input even less likely. Alternatively, it is possible that a switch does occur, but in conditions that we did not evaluate. One such condition is during high stimulus intensities, where elevated auditory nerve spike rates would increase the probability of coincident input within a stimulus period while simultaneously subjecting each unitary input to pronounced short-term synaptic depression. NM neurons also receive depolarizing GABAergic inhibition from the SON during intense stimulation (Fukui et al., 2010), which would act to narrow the integration period at the same time that NM neurons would be receiving a greater number of depressed inputs per period. Indeed, Fukui et al. (2010) demonstrated that GABA block degraded phase-locking precision in NM. Together, synaptic depression and recruitment of inhibition could dynamically adjust the optimal integration strategy from relay to integrate and fire.

The cochlear nucleus has been observed to improve phase-locking precision to low-frequency sounds in other species as well, including barn owls at frequencies <1000 Hz (Sullivan and Konishi, 1984; Köppl, 1997) and mammals; cats <700 Hz (Joris et al., 1994), chinchillas <600 Hz (Recio-Spinoso, 2012), and rats <1000 Hz (Paolini et al., 2001). In spherical bushy cells of the mammalian cochlear nucleus, analogs of NM neurons, convergence of multiple subthreshold inputs, and a fast membrane time constant have been previously proposed as mechanisms for improving phase-locking to low-frequency stimuli, whereas a single input would provide stronger phase-locking to higher stimulus frequencies (Rothman et al., 1993; Joris et al., 1994; Burkitt and Clark, 1999; Xu-Friedman and Regehr, 2005a). Recruitment of inhibitory input to bushy cells attenuates spike rates (Caspary et al., 1994; Paolini and Clark, 1998; Kopp-Scheinpflug et al., 2002; Kuenzel et al., 2015) and has been shown to improve phase-locking precision (Englitz et al., 2009; Keine and Rübsamen, 2015). Finally, whole-cell recordings in mouse spherical bushy cells demonstrated that inhibition can mediate a mode switch from relay of single superthreshold enbulb inputs to integration of two subthreshold inputs through both presynaptic and postsynaptic mechanisms, potentially improving spike timing in the process (Xu-Friedman and Regehr, 2005b; Chanda and Xu-Friedman, 2010). Inhibition's influence on mammalian spherical bushy cells, together with the in vivo results from the chick NM described by Fukui et al. (2010), strongly suggest that inhibition may provide a similar computational function in NM. Biophysical evidence from whole-cell recordings to test this prediction in NM will require further investigation.

In conclusion, we engaged the chicken's tonotopic map in the cochlear nucleus to systematically investigate optimal input-output characteristics of neurons across the frequency domain. We demonstrated that the gradients of progressively lower input resistances and higher spike thresholds across the tonotopy underlie two differential computational processes across the tonotopic axis. Our modeling and empirical data showed that the optimum input number is specified by stimulus frequency, such that phase-locking to low-stimulus frequencies was always improved by integration of many inputs, whereas high frequencies were always best represented with a single input. Postsynaptically, expression of K_LVA does not confer added precision to LCF processing but primarily allows MCF and HCF neurons to reject poorly timed inputs that occur across stimulus periods. These data, together, identify specific synaptic and postsynaptic characteristics that allow auditory neurons to compute with temporal precision. Although our findings benefit from the experimentally advantageous tonotopic arrangement in the chick cochlear nucleus, these principles are likely to apply to all neurons that compute with temporal precision across a similar frequency range.