Computational nanomedicine: modeling of nanoparticle-mediated hyperthermal cancer therapy

Abstract

Nanoparticle-mediated hyperthermia for cancer therapy is a growing area of cancer nanomedicine because of the potential for localized and targeted destruction of cancer cells. Localized hyperthermal effects are dependent on many factors, including nanoparticle size and shape, excitation wavelength and power, and tissue properties. Computational modeling is an important tool for investigating and optimizing these parameters. In this review, we focus on computational modeling of magnetic and gold nanoparticle-mediated hyperthermia, followed by a discussion of new opportunities and challenges.

Nanoparticles are desirable for biomedical applications because of their distinctive chemical and physical properties, which facilitate the targeting of specific cell types, improve pharmacokinetics and bioavailability, and enhance signal detection [1,2]. Numerous nanoparticle drugs for different diseases are currently in the drug development pipeline [3], and US FDA approval has been granted to several nanoparticle drugs, including nanoparticle albumin-bound paclitaxel (Abraxane®), and liposomal formulations of doxorubicin (Doxil®), daunorubicin (DaunoXome®) and cytarabine (DepoCyt®), for treatment of different cancers [4]. Nanoparticle-based therapeutics are not restricted to nanoparticle drug formulations; a growing area of research in cancer therapy is nanoparticle-based hyperthermia [5], in which nanoparticles administered to a tumor are heated in order to kill cancer cells.

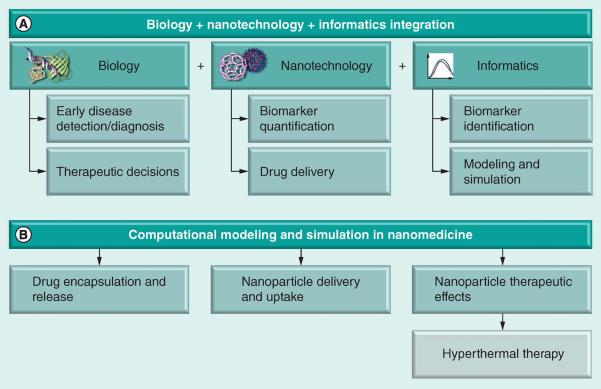
These advances demonstrate that there has been considerable progress in nano- and biotechnology over the last several years. However, several key challenges have also become apparent, including the need for a better understanding of nanoparticle behavior in vivo and the development of more effective nanoparticle therapeutics [6]. Computational efforts are becoming an important tool in addressing both of these challenges, as well as in generally facilitating and accelerating nanotechnology-based translational research. For example, ‘nanoinformatics’ has arisen as a new research area that covers raw data management (i.e., nomenclatures and classification of nanomaterials, such as quantum dots), analysis of the data derived from biomedical applications (i.e., processing and data mining of nanoparticle-based imaging) and simulation of nanoparticle interactions with biological systems [7]. Figure 1 depicts the integration of biology, nanotechnology and informatics to form the basis for computational nanomedicine.

Figure 1.

Computational methods for nanomedicine

Informatics methods are critical in the application of nanotechnology to solve biological problems. In order to effectively detect and treat disease, the identification of specific biomarkers or nanodrug targets that minimize adverse reactions and side effects while also maximizing therapeutic efficacy is required [4]. Bioinformatics methods of drug target discovery vary from indirect genomic screening to direct proteomic assays and from simple data mining to complex network and system modeling. Many genomic biomarker identification methods have been developed for specific technologies, including microarrays [8] and, more recently, next-generation sequencing [9]. Network modeling has also been used to identify potential drug– biomarker interactions [10], as well as systems-level approaches to elucidate the therapeutic and adverse effects of drugs [11]. Quantification of nanoparticle activity via enhanced imaging techniques is necessary both during experimental development of a treatment (to assess targeting specificity) and during application (to monitor drug efficacy) [12]. Multispectral or hyperspectral image processing techniques are applicable to a variety of nanoparticle-enhanced imaging data [13]. Innovative algorithms have emerged for tracking particles, such as quantum dots, within cells [14–16].

This review describes recent developments in computational modeling and simulation (one component of informatics) in nanomedicine (Figure 1B). The nanoparticle therapeutics pipeline is a complex process involving multiple steps. Computational modeling has become an essential tool for understanding complex biological processes. Indeed, modeling has been considered to be among seven key priorities for enabling translation of nanomedicine from the laboratory to the clinic [17,18]. Numerous computational models have been developed to study the key steps in the nanomedicine pipeline, such as drug encapsulation and release [19,20], nanoparticle targeting, delivery and uptake [17,21–25], and nanoparticle effects on cells and tissues [26–27]. In particular, this article reviews recent progress in the development of computational models for a specific class of nanoparticle-based therapies: nanoparticle-mediated hyperthermia. This is a form of cancer therapy in which the nanoparticle, rather than a nanoparticle-encapsulated drug, is the basis for treatment.

Nanoparticle-based hyperthermia for cancer treatment

Hyperthermia, or thermal therapy, is a form of cancer therapy in which the tumor is heated, causing damage and cell death. Typical temperature ranges for therapeutic hyperthermia are between 40 and 45°C. As a result of heating, a number of molecular effects take place, including protein denaturation and the induction of apoptosis [28–31]. Cancer cells are not intrinsically more vulnerable to hyperthermia than normal cells; however, in vivo, the low pH and hypoxic microenvironment associated with tumors increase the sensitivity of cancer cells to hyperthermia [32]. In addition, hyperthermia is usually applied in combination with either chemotherapy or radiation therapy. Numerous studies have demonstrated thermal sensitization, where the combination of hyperthermia and chemotherapy, or hyperthermia and radiation is more effective than either chemotherapy or radiation alone; detailed reviews on this topic are available elsewhere [28,33].

Depending on the tumor type, size and location, hyperthermia may be applied locally, regionally or over the whole body [5,34]. Heat can be delivered via different mechanisms depending on the extent of application; for example, energy sources may include ultrasound, thermal chambers or laser light [34,35]. Nanoparticles provide an interesting mode of application for hyperthermia, because by concentrating the local heat source (the nanoparticles) within the tumor, heat-induced damage to healthy cells can, in theory, be minimized. In addition, nanoparticles provide a vehicle for delivering chemotherapeutic drugs to the tumor at the same time that hyperthermia is induced [36]; such composite nanoparticles could take direct advantage of chemosensitization effects.

The primary types of nanoparticles being studied in computational models of hyperthermal therapy are magnetic nanoparticles – specifically the biocompatible iron oxides, magnetite (Fe3O4) and maghemite (γ-Fe2O3) – and gold nanomaterials of various shapes [35,37,38]. Laurent and colleagues provide an in-depth review of superparamagnetic iron oxide nanoparticles for hyperthermia [39]. Carbon nanotubes are also being investigated for hyperthermal therapy [40,41]. The feasibility of magnetic nanoparticle-based hyperthermia is being evaluated in patient studies for several types of tumors, including prostate cancer and glioblastoma multiforme [42–48]. A clinical pilot study of commercialized gold nanoshells, AuroShell®, is currently recruiting patients [49, 101].

In magnetic fluid hyperthermia, magnetic nanoparticles are introduced to the tumor via arterial or direct injection, in situ implants or active targeting [39]. The patient is then exposed to an alternating magnetic field. Heat is generated as a consequence of the rotation of magnetic moments of the nanoparticles to align with the magnetic field by a combination of Brownian and Néel relaxations. A limiting factor observed in an early patient trial is irregular intratumoral heating [45]. In gold nanomaterial-based hyperthermia, the nanoparticle excitation is typically done through a near-infrared laser light source [35,49]. Heat is generated as the particles absorb the light and increase in temperature. Gold nanoparticles are capable of generating high temperatures, but a limiting factor for this method is the penetration depth of near-infrared light into tissue [50]. The key challenge for both magnetic and gold nanoparticle-mediated hyperthermia is identifying the best nanoparticle concentrations, spatial distributions and excitation source parameters to inflict fatal thermal damage to cancerous tissues, while minimizing the damage to surrounding healthy tissues. Computational modeling studies for nanoparticle-mediated hyperthermia have focused on addressing these questions.

Computational modeling of nanoparticle-based hyperthermia

In this section, we first provide an overview of hyperthermia modeling, including the key nanoparticle, excitation source and tissue properties studied. Next, we use two recently published models of nanoparticle-mediated hyperthermia as case studies to illustrate the modeling process in greater depth. Finally, we summarize and discuss recent progress in modeling magnetic and gold nanoparticle-mediated hyperthermia.

Key aspects of modeling nanoparticle-mediated hyperthermia

Box 1 provides an overview of the variables and parameters that have been examined in many recent models of nanoparticle-mediated hyperthermia. Some models focus more on the physics of the process, investigating the behavior of a certain type of nanoparticle under different degrees of excitation and the resulting heating effects on the surrounding media. Others are more focused on the therapeutic aspect of hyperthermia, and explicitly describe the effects of nanoparticle heating on biological tissues. In studies that model the heating of tumor tissue, Pennes’ bioheat equation is typically applied. This is a partial differential equation that relates tissue temperature to several physiological and environmental factors such as externally applied heat, metabolically generated heat and blood perfusion.

Case study: comparison of two nanoparticle-mediated hyperthermia models

In this section, we describe in detail two different models that highlight different aspects of hyperthermia modeling in a complementary manner. One model describes magnetic fluid hyperthermia in vivo, at the tissue-level, while the other describes gold nanorod-based hyperthermia in vitro, and describes nanorod-cell interactions. Both models have been evaluated using experimental temperature measurements over time, and the model predictions showed good agreement with experimental results. Key mathematical formulations shown in this case study, such as those for Brownian and Néel relaxations and the Pennes’ bioheat equation, are widely used in many nanoparticle-mediated hyperthermia models.

First, we examine the components of the model for magnetic nanoparticle-mediated hyperthermia published by [51]. Key model equations (Equations 1–6) are listed with a description of the terms and variables in Table 1.

Table 1.

Description of terms and variables in model of Liangruksa et al.

Equation no.	Equation	Description	Variables	Description of variables
1	${\tau }_B=\frac{3\eta V_H}{k_{B}T}$	Brownian relaxation	T	Temperature (degrees)
			η	Viscosity (pressure · time)
			VH	Hydrodynamic particle volume (volume)
			kB	Boltzmann's constant (energy · degrees−1)
2	${\tau }_N=\sqrt{\pi }{\tau }_0\frac{e^{\left[\frac{K_{\alpha }{V}_m}{k_{B}T}\right]}}{2\sqrt{\frac{K_{\alpha }{V}_m}{k_{B}T}}}$	Néel relaxation	VM	Magnetic particle volume (volume)
			Kα	Magnetic anisotropy constant (energy · volume−1)
			τ 0	Larmor time constant (time)
3	$\tau =\frac{{\tau }_B{\tau }_N}{({\tau }_B+{\tau }_N)}$	Overall relaxation time
4	$P=\pi {\mu }_0{H}_0^2{x}^{″}f$	Magnetic heating (energy dissipation)	μ 0	Magnetic permeability of vacuum (force · current −2)
			H0	Amplitude of alternating magnetic field (current · length−1)
			f	Frequency (time−1)
			χ · ·	Imaginary part of magnetic susceptibility (unitless)
5	${\chi }^{″}=\frac{\omega \tau {\chi }_0}{1+{\left(\omega \tau \right)}^2}$	Imaginary part of magnetic susceptibility	ω	Rotational frequency of magnetic field (rad · time−1)
			τ	Relaxation time (time)
			χ 0	Static magnetic susceptibility of ferrofluid-dosed tumor (unitless)
6	${\rho }_{\tau }{c}_{\tau }\frac{\partial T_t}{\partial t}=\left(\frac{k_t}{r^2}\right)\frac{\partial }{\partial r}\left(r^2\frac{\partial T_t}{\partial r}\right)-m_b{c}_b(T_t-T_b)+P$	Temperature in tumor tissue (Pennes’ bioheat transfer equation)
6A	${\rho }_{\tau }{c}_{\tau }\frac{\partial T_t}{\partial t}$	Weighted change in tissue temperature	Tt	Tissue temperature (degrees)
			ρ t	Tissue mass density (mass · volume−1)
			cτ	Specific heat of tissue (energy · mass−1 · degrees−1)
6B	$\left(\frac{k_t}{r^2}\right)\frac{\partial }{\partial r}\left(r^2\frac{\partial T_t}{\partial r}\right)$	Heat conduction	kt	Tumor thermal conductivity (power · length−1 · degree−1)
			r	Radius (length)
6C	mbcb(Tt – Tb)	Advection by blood perfusion	Tb	Basal temperature (degrees)
			cb	Specific heat of blood (energy · mass−1 · degrees−1)
mb	Blood perfusion (mass · volume−1 · time−1)

Equations are taken from the model by Liangruksa et al. [51].

The change in magnetization of magnetic nanoparticles causes heat generation; different aspects of this process are described by Equations 1–5. For magnetic particles, hysteresis losses and relaxation losses can contribute to heat generation. The effects of these mechanisms are a function of parameters of the alternating magnetic field and the nanoparticle size [36]. For alternating magnetic field frequencies applied to clinical applications, relaxation is predominant. Two types of relaxation can occur: Néel relaxation τN, in which the magnetic moment of the nanoparticle rotates to align with the applied magnetic field, or Brownian relaxation τB, in which the nanoparticle physically rotates to align with the field. The equations for these two processes are given in Equations 1 & 2. Both processes occur in parallel, thus, the overall relaxation time is given by Equation 3.

The relaxation time is a variable in the overall magnetic heating, which is described by the Debye model in Equations 4 & 5. This model, which describes volumetric power dissipation, is also a function of parameters of the alternating magnetic field and the magnetic ferrofluid. Magnetic heating is related to tumor tissue heating by Equation 6, which describes the Pennes’ bioheat transfer equation in spherical coordinates. This equation relates the change in tumor tissue temperature to heat conduction (diffusion) in the tissue, advection by blood perfusion and heat generation by nanoparticles. Heat conduction and advection are a function of tissue properties – thermal conductivity, blood perfusion, specific heats of blood and tissue, and tissue density – and the nanoparticle heat generation from Equation 4.

Next, we examine the components of the model for gold nanorod-mediated hyperthermia published by Huang et al. [37]. Key model equations (Equations 7–11) are listed with a description of the terms and variables in Table 2.

Table 2.

Description of terms and variables in model by Huang et al.

Equation no.	Equation	Description	Variables	Description of variables
7	$\frac{\partial T}{\partial t}=\alpha {\nabla }^{2}T+\frac{Q}{\rho C_D}(1-{10}^{-OD})$	Heat transport
7A	α ∇ 2 T	Heat conduction	T	Temperature (degrees)
			α	Tissue or fluid thermal diffusivity (area · time−1)
7B	$\frac{Q}{\rho C_p}(1-{10}^{-OD})$	Heat from laser-irradiated gold nanorods	Q	Laser energy (power · volume−1)
			ρ	Tissue or fluid density (mass · volume−1)
			Cp	Tissue or fluid heat capacity (energy · mass−1 · degrees−1)
			OD	Optical density (unitless)
8	$k\frac{\partial T}{\partial n}=U(T-T_0)$	Boundary condition for temperature of surroundings	U	Heat transfer coefficient for region neighboring boundary (power · area−1 · degrees−1)
			T0	Bulk temperature of surroundings (degrees)
			k	Scaling constant (power · length−1 · degrees−1)
9	$k=A{e}^{-\frac{E_{\alpha }}{RT}}$	Heat-induced cell injury	A	Scaling factor (time−1)
			Eα	Activation energy (energy · mol−1)
			R	Gas constant (energy · degree−1 · mol−1)
10	$F_D=1-e^{-{\int }_0^{t}kdt}$	Tissue injury as an aggregate of cell injury	k	Cell injury rate (time−1)
11	$\frac{\partial C_b}{\partial t}=k_{\alpha }{C}_{bs}C-k_d{C}_b$	Cell–nanorod interactions
11A	kαCbsC	Binding of free nanorods to open binding sites	kα	Binding association rate (time−1)
			Cbs	Open binding sites (concentration)
			C	Free nanorods (concentration)
11B	kdCb	Dissociation of nanorods from binding sites	kd	Binding dissociation rate (time−1)
			Cb	Nanoparticles bound to binding sites (concentration)

Equations are taken from the model by Huang et al. [37].

Heat transfer is described by Equations 7 & 8. Equation 7 describes the change in tissue temperature over time as a function of heat diffusion and the heat contributed by laser-irradiated gold nanorods. Equation 7A describes the contribution of heat diffusion to the change in temperature; as Huang and colleagues note, this is based on the Pennes’ bioheat equation. However, the complete Pennes’ equation, which also considers terms such as blood perfusion and metabolic heat generation, was not used in this model because the experimental system is in vitro. Equation 7B describes the contribution of heat from the laser-irradiated gold nanorods to the change in temperature. This is a function of the laser energy, the thermal properties of the medium and the concentration (in terms of optical density) of the nanorods.

Cell and tissue injury due to hyperthermia is described by Equations 9 & 10. These equations describe the Arrhenius injury model, which is a commonly used model for describing heat-induced cell injury. Equation 9 describes how both environmental (temperature and the gas constant), and cell- and tissue-specific (activation energy and scaling factor) variables are considered to describe the rate of cell injury. Equation 10 integrates the cell injury rate over time to describe the overall fraction of injured tissue FD, such that FD = 0 for healthy and FD = 1 for dead tissue, respectively. The distribution of nanorods between bound and unbound states is described by Equation 11. Huang and colleagues argue that because the nanorods exhibit low diffusivity in water and tissue, and because the internalization rate of nanorods into cells after binding is considerably lower than the rate of unbinding, the distribution of nanorod states can be described only in terms of bound and free nanorods. As such, Equation 11 describes the change in the concentration of nanorods bound to the cell surface as a mass action model. In this description, the rate of change equals the difference between the binding of free nanorods to open binding sites and the dissociation of already bound nanorods from the cell.

The goal of these case studies is to highlight some practicalities of the modeling process by illustrating how different models describe related, but distinct, processes. For example, both the magnetic and gold nanoparticle models use Pennes’ bioheat transfer equation, but they use different variations of it. The model by Liangruksa et al. describes the physics behind magnetic nanoparticle heating in detail, but does not describe cell–nanoparticle interactions, and assumes a spherical tumor in vivo [51]. The model by Huang et al. describes laser excitation of gold nanorods in only a single equation, but incorporates the Arrhenius cell injury model and cell–nanoparticle interactions for an in vitro cell population [37]. As the field of nanoparticle-mediated hyperthermia modeling grows and develops, it is feasible that more comprehensive models will be developed for specific nanoparticle types, which incorporate both details about the nanoparticle excitation process and details of cell–nanoparticle interactions, and of cell and tissue damage. It is possible that such comprehensive models, specific to a particular experimental or clinical scenario, could be assembled from model ‘libraries’ containing well-accepted mathematical modules for different aspects of nanoparticle hyperthermal therapies.

Recent progress in modeling magnetic fluid hyperthermia

Recent modeling studies have investigated the properties of both magnetic nanoparticles and the applied magnetic field, with different models considering different combinations of properties. The properties include the magnetic field strength and frequency [36,52,53], eddy current generation [54], nanoparticle mass and size [36,52,55], concentration [52], nanoparticle agglomerates [56] and nanoparticle spatial distributions [38,57,58].

Notably, several recent modeling studies for magnetic nanoparticle-mediated hyperthermia have focused on optimization. Salloum and colleagues considered two irregular tumor shapes embedded in a block of normal tissue, and multiple nanoparticle injection sites [38]. The nanoparticle efficiency of heat generation in hyperthermia is often described by the specific absorption rate (SAR), and this study modeled the SAR as a function of A, the maximum value at the injection site, and r 0, the distance from the injection site that the tissue is heated. This study presented a method for identifying the values of A and r 0 that optimize the SAR and achieve appropriate temperatures in both the tumor and normal tissue by considering the nanoparticle injection locations, the thermal properties of both tissue types and blood perfusion rates.

Mital and Tafreshi focused on optimizing two parameters that govern the externally applied heat: r 0 and the time constant τ of its exponential decay function [59]. While the study used concentric spheres to represent the tumor and normal tissue, the model used a finite element solution to Pennes’ bioheat equation, which could be extended to more realistic tumor morphologies. Sensitivity analysis for the model indicated that the blood volumetric heat capacity, perfusion and thermal conductivity were key parameters, while metabolic heat generation was less important.

Notably, Cervadoro et al. performed a combined experimental and modeling study to compare commercially available superparamagnetic iron oxide nanoparticles and identified the properties needed – nanoparticle concentrations, alternating magnetic field parameters and blood perfusion levels – to achieve hyperthermia or tissue ablation [50]. Such optimization studies, particularly if integrated with clinical imaging data, could provide valuable insight for magnetic nanoparticle-mediated hyperthermia therapy planning.

Recent progress in modeling gold nanomaterial-based hyperthermia

Different models have considered different types of gold nanomaterials: spherical nanoparticles [60–62], nanorods [37] and nanoshells [62,63]. As with magnetic nanoparticles, recent studies for gold nanomaterials have investigated the effects of different experimental and biological conditions. These include laser pulse duration and frequency [61,64], irradiation time and nanoparticle concentration [37], differentiation between heating resulting from the laser versus the nanoparticles [63] and the effects of heating on different organelles within the cells [61].

The results of a recent modeling study for gold nanoparticles have shown that the effect of vapor formation, and changes in the thermal conductivity and dielectric properties of the surrounding medium are important experimental factors [62]. This particular study also noted that, if the dielectric and thermal changes are not considered, the estimated temperature of the nanoparticle surroundings will be much higher – an observation that has clear implications for treatment planning.

In the model described previously, Huang et al. investigated how the increased susceptibility of cancerous cells to hyperthermia could be combined with targeted gold nanoparticle binding in order to increase the selective killing of cancer cells [37]. By simulating increased heat sensitivity for cancer cells compared with normal cells, and increasing the gold nanoparticle concentration near cancer cells, the authors predicted that relatively small changes in both parameters would yield a multiplicative effect in terms of the percentage of cancer cells killed compared with the percentage of healthy cells.

A third modeling study demonstrated that, owing to their specific heat and the thermal conductivity of the medium, cellular organelles undergo accumulative heating in the presence of gold nanoparticles excited by multipulse lasers, while the nanoparticles themselves do not [61]. This observation could provide a practical advantage because laser energy density can be lowered in the multipulse mode. Another prediction of this study was that the nuclei of healthy cells would become heated to a damaging temperature before cancerous nuclei. The results of these studies emphasize the relevance and potential of nanoparticle targeting in hyperthermia [37,61], which is also discussed by Letfullin et al. [65].

Conclusion & future perspective

We have highlighted several challenges and opportunities related to the computational modeling of nanoparticle-based hyperthermia (Box 2). An important challenge is the development of models that consider the effects of tumor structure and heterogeneity. Some modeling studies focus solely on nanoparticle effects and do not explicitly model tissue heating [62]. Among those that do model the tumor, many assume a spherical tumor for simplicity of computation [36,51,57,59,60]. Real tumors, however, may have highly irregular shapes. One recent study addresses this spatial aspect by developing a mathematical model for magnetic nanoparticle hyperthermia treatment planning targeted at tumors with irregular morphologies [38].

Modeling nanoparticle distribution within the tumor is a related issue. For example, several studies assume a homogeneous tumor with nanoparticles spread uniformly throughout the region [36,53,60]. In practice, nanoparticle distribution may be uneven; this has been observed in vivo in human patients and attributed to administration methods [48]. In addition, tumor heterogeneity presents an obstacle to targeted nanoparticle delivery [66]. Moreover, high interstitial pressure in tumors and the extracellular matrix may also contribute to uneven nanoparticle distribution by providing a barrier to diffusion [67]. An important related issue is the targeting of nanoparticles; computational models of this process have been discussed in detail in a recent review [17].

Another notable challenge is the modeling of combination effects between hyperthermia and chemotherapy, and between hyperthermia and radiation. Purushotham and Ramanujan touch upon this issue by modeling drug release from doxorubicin-loaded magnetic nanoparticles during hyperthermia [36]. However, different drugs are associated with different extents and mechanisms of effects from hyperthermia [32,33]. Integrating models of hyperthermia with multiscale models of drug response [68] could be a useful direction for research, as is the development of mechanistic models of heat-induced cell death and thermotolerance [69,70].

The development of commercial modeling tools is also an important step for advancing nanoparticle-mediated hyperthermia, because it would make computational modeling more accessible to a larger clinical audience. However, to the authors’ knowledge, there is currently only one such tool that specifically targets nanoparticle-mediated hyperthermia: NanoPlan® (MagForce AG, Berlin, Germany) can predict tissue temperatures given the nanoparticle distribution. This tool has been used in several clinical feasibility studies for magnetic nanoparticle-mediated hyperthermia at the Charité-University Medicine in Berlin (Germany) [39].

On a broader level, an important challenge is the integration of modeling and experimental studies for the purpose of translational research. Many of the papers described in this review are purely in silico studies, without tandem experimental verification. In order for mathematical models to be effectively used in experimental and clinical settings, it is necessary that model development, verification and validation occur in a feedback cycle with respect to in vitro and in vivo observations.

While notable progress has been made towards the application of nanoparticles in medicine, many complexities remain to be understood [71]. As recent research has shown, computational modeling can predict how different properties affect nanoparticle behavior and tissue response in a complex environment, and can thereby guide experimental research. We speculate that over the next 5–10 years, the combination of clinical image analysis and modeling [19,52,72] will be incorporated into nanoparticle-mediated hyperthermia models, enabling more personalized treatment strategies. In addition, tools and techniques that have been established for conventional hyperthermia, such as commercial treatment planning software and control theory-based models [73], will be extended to nanoparticle-based hyperthermia. Such computational developments, in parallel with experimental advancements and clinical studies for different types of nanoparticles, will help to realize the clinical potential of nanoparticle-mediated hyperthermia cancer therapy.

Executive summary.

Nanoparticle-based hyperthermia for cancer treatment

• ■ Nanoparticles are being investigated as a heat source for hyperthermal cancer therapy. The advantage of this method compared with conventional hyperthermia is the potential of localized heating of cancer cells, minimizing the effects on the surrounding healthy tissue.

Computational modeling for nanoparticle-mediated hyperthermia

• ■ Computational models are used to investigate how nanoparticle physical characteristics, excitation sources and biological tissue properties affect therapeutic performance.

• ■ Numerous models have been developed in recent years for investigating these factors for magnetic nanoparticles and gold nanospheres, nanorods and nanoshells.

• ■ Challenges and opportunities include models integrating personalized patient imaging data, and models of combined nanoparticle-based hyperthermia and chemotherapy.

Box 1.

Notable variables and parameters in computational models of nanoparticle-mediated hyperthermia.

Nanoparticle physical properties

■ Material

– Iron (magnetic and superparamagnetic)

– Gold

■ Size

■ Shape

– Nanospheres

– Nanorods

– Nanoshells

– Agglomerates

Excitation source properties

■ Alternating magnetic fields

– Strength

– Frequency

– Eddy currents

■ Laser sources

– Strength

– Duration

– Frequency

Tissue properties

■ Intrinsic

– Bioheat transfer

– Specific heat of tissue and blood

– Tissue and blood density, tissue thermal conductivity and blood perfusion

– Arterial temperature

– Metabolic heat generation and applied heat

– Shape and heterogeneity

■ Nanoparticles in tissue

– Concentration

– Spatial distribution

Box 2.

Challenges, progress and opportunities in the computational modeling of nanoparticle-mediated hyperthermia.

Challenges

■ Model-guided experimental design

■ Optimization of nanoparticle properties and excitation

■ Development of personalized therapeutic strategies

Progress

■ Models investigating how the efficacy of hyperthermia for cancer treatment is affected by variations in:

– Nanoparticle properties

– Excitation sources

– Biological tissue properties

Opportunities

■ Models describing tumor heterogeneity

■ Models investigating combination therapies and resistance

■ Greater integration of experimental and theoretical studies

■ Adoption of clinical molecular imaging to personalize treatment