Figure 3. Experimental determination of perturbation‐induced stepping threshold .
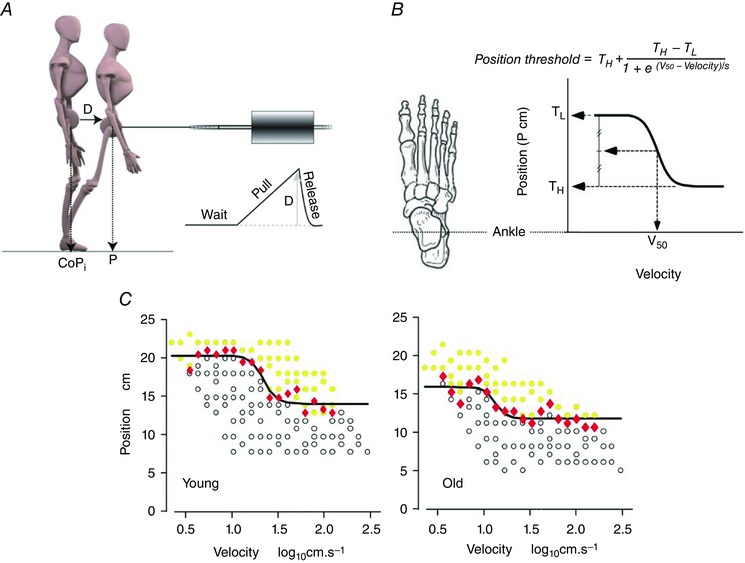
Younger and older adults received 124 randomly applied displacement‐velocity forward waist‐pull perturbations to determine the threshold for triggering induced stepping. A, the threshold for forward‐induced stepping was determined using a linear‐motor pulling the subject forward via a flexible cable attached around the upper pelvis. The pulls started at an unexpected time and proceeded at the test velocity until, on reaching the test displacement (D), the cable tension is released and the subject can lean back if a step has not already been initiated. This is illustrated in the pull displacement profile (D) as a function of time. The initial position of the subject was estimated from the initial location of the centre of pressure (CoPi) relative to the ankle joint centre. D was added to the CoPi to estimate the final position of the pelvis at the end of the pull relative to the ankle (P). This reflected how far in front of the axis of the ankles the pelvis moved at the end of the pull. B, the threshold boundary was then described using a modified Boltzmann function, which is a negative, inverse exponential of velocity. Four parameters, represented in the graph, described the low‐velocity plateau (T L) and the high‐velocity plateau (T H) levels, the velocity that produces the mid‐range response (V 50), and the slope (S). The inverse of the slope is directly proportional to the maximal steepness of the function, which occurs at mid‐range. C, typical stepping records for a young and an older subject. Each circle corresponds to a pull trial, marked as either a step (yellow) or no step (white). At each velocity, a threshold position (red diamond) was identified half way between the most anterior position (largest value) that did not produce a step and the most posterior position (smallest value) that produced a step. The Boltzmann function was fitted (Gauss–Newton non‐linear least‐mean‐squares algorithm) to these threshold position points to describe the threshold boundary (continuous line). (Adapted from Mille et al. 2003.)
