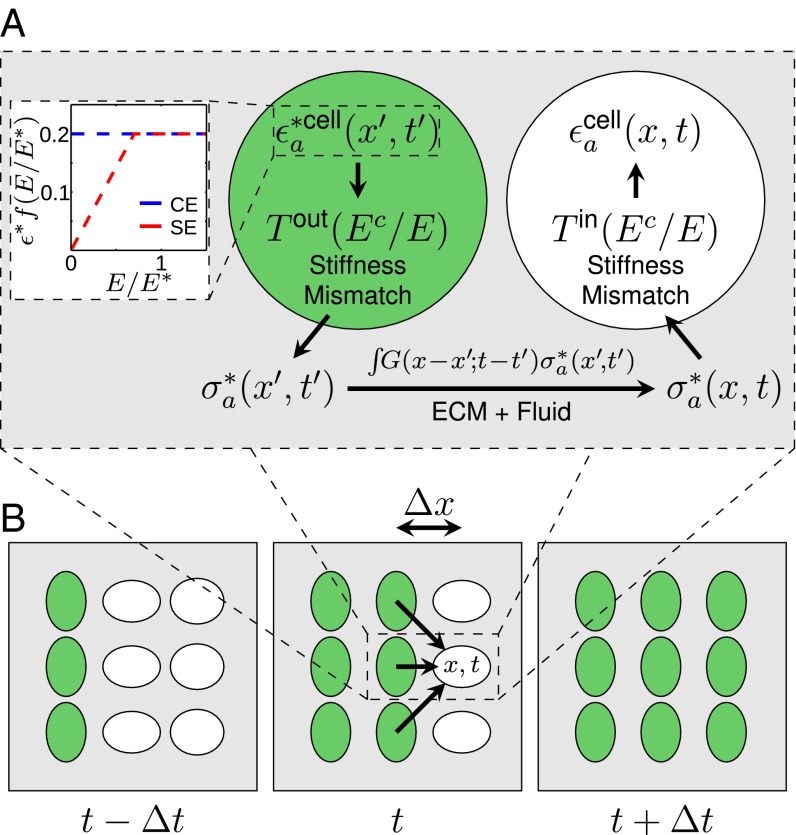
Fig. 1.

Model for stress propagation in the myocardium. (A, Inset) CE and SE models as a function of ECM Young’s modulus, which determines the strength of contraction (Eq. 1). (Main) The contracting CM (green) acts as a stress source for a quiescent CM (white). An activated cell a contracts with an eigenstrain ${\mathit{ϵ}\ast }_{a,ij}^{\text{cell}}\left(x\prime ,t\prime \right)$, locally inducing a stress ${\sigma \ast }_{a,ij}\left(x\prime ,t\prime \right)$ in the ECM that depends on the relative stiffness between the ECM and CMs. We capture these physics via the tensor $T_{ijkl}^{\text{out}}$ in accordance with the Eshelby theory of elastic inclusions (Supporting Information). This stress propagates according to the ECM response function $G_{ijkl}\left(x-x\prime ,t-t\prime \right)$ (Supporting Information). The matrix stress at $\left(x,t\right)$ due to cell a is ${\sigma }_{a,ij}\left(x,t\right)={\displaystyle \int d^{3}x\prime dt\prime G_{ijkl}\left(x-x\prime ,t-t\prime \right){\sigma \ast }_{a,kl}\left(x\prime ,t\prime \right)}$. This creates ${\mathit{ϵ}}_{a,ij}^{\text{cell}}\left(x,t\right)$, the strain induced in the quiescent CM due to the contraction of a (modified by $T_{ijkl}^{\text{in}}$). (B) Sketch depicting quiescent (white) and activated (green) CMs in a traveling mechanical wave front at subsequent activation times separated by $\mathrm{\Delta }t$. Arrows represent stresses propagated through the ECM (not all shown) to a quiescent CM, which activates when ${\mathit{ϵ}}_{ii}^{\text{cell}}\left(x,t\right)\ge \alpha$.