Noninvasive Failure Load Prediction of Vertebrae with Simulated Lytic Defects and Biomaterial Augmentation

Abstract

The spine is the most common site for secondary bone metastases, and clinical management for fractures is based on size and geometry of the defect. About 75% of the bone needs to be damaged before lesions are detectable, so clinical tools should measure changes in both geometry and material properties. We have developed an automated, user-friendly, Spine Cancer Assessment (SCA) image-based analysis method that builds on a platform designed for clinical practice providing failure characteristics of vertebrae. The objectives of this study were to (1) validate SCA predictions with experimental failure load outcomes; (2) evaluate the planning capabilities for prophylactic vertebroplasty procedures; and (3) investigate the effect of computed tomography (CT) protocols on predicted failure loads. Twenty-one vertebrae were randomly divided into two groups: (1) simulated defect without treatment (negative control) [n = 9] and (2) with treatment [n = 12]. Defects were created and a polymeric biomaterial was injected into the vertebrae in the treated-defect group. Spines were scanned, reconstructed with two algorithms, and analyzed for fracture loads. To virtually plan for prophylactic intervention, vertebrae with empty lesions were simulated to be augmented with either poly(methyl methacrylate) (PMMA) or a novel bone replacement copolymer, poly(propylene fumarate-co-caprolactone) [P(PF-co-CL)]. Axial rigidities were calculated from the CT images. Failure loads, determined from the cross section with the lowest axial rigidity, were compared with experimental values. Predicted loads correlated well with experimental outcomes (R² = 0.73, p < 0.0001). Predictions from negative control specimens highly correlated with measured values (R² = 0.90, p < 0.0001). Although a similar correlation was obtained using both algorithms, the smooth reconstruction (B30) tended to underestimate predicted failure loads by ∼50% compared with the ∼10% underestimate of the sharp reconstruction (B70). Percent increase in failure loads after virtual vertebroplasty showed a higher increase in samples with PMMA compared with those with copolymer. The SCA method developed in this study calculated failure loads from quantitative computed tomography scans in vertebrae with simulated metastatic lytic defects, with or without treatment, facilitating clinical applicability and providing more reliable guidelines for physicians to select appropriate treatment options. Furthermore, the analysis could accommodate augmentation planning procedures that aimed to determine the optimum material that would increase vertebral body failure load.

Introduction

In 2014, cancer affected an estimated 14.5 million persons in the United States, and 1.6 million new cancer cases are anticipated in 2016.¹ About half of these patients will have secondary bone metastases,^2,3 with the marrow-rich vertebral column being the most common site of tumor deposition.⁴ The spine is a load-bearing structure and failure of its structural integrity as a consequence of metastatic vertebrae, large lesion size, and vertebral body collapse can lead to narrowing of the spinal canal, spine curvature changes, pulmonary compromise, pain, and additional decrements in quality of life (e.g., depression, insomnia).^5,6

Of the cancers that metastasize to the spine, the most common is breast cancer (prevalence, 21%), and 17% to 50% of affected patients sustain a vertebral body fracture.⁷ With patient longevity increasing through advances in medical treatment, in conjunction with the existing demographic shift toward an elderly population, vertebral fractures after metastasis will be a significant challenge to current healthcare systems.

Plain radiographs, which are used to detect the size and geometry of the osteolytic defect, can often predict vertebral fracture after metastasis. However, 50% to 75% of the bone needs to be damaged before the defect is detectable.⁸ The paucity of accurate and objective criteria has motivated development of several scoring systems to evaluate the structure of vertebrae with metastatic tumors. Taneichi et al.⁹ used a multivariate logistic regression model to suggest a scheme for determining risk factors for structural vertebral collapse. However, the analysis is of limited use in clinical practice because it is time-consuming and does not account for the geometry or quality of the remaining bone. Mirels¹⁰ proposed a scoring system that quantified the risk of sustaining a fracture in a long bone by combining four roentgenographic and clinical risk factors into a single score. Although these scoring systems provide some clinical guidance regarding a surgical decision, they are still inherently qualitative assessments.

To provide a more accurate determination of fracture risk in the setting of metastatic vertebral disease, clinical tools should measure changes in bone mineral density (BMD) and load-bearing capacity of the vertebral body. One possible method incorporates quantitative computed tomography (QCT), which can delineate the geometry of the lesion in the vertebrae and quantitatively estimate BMD. Axial rigidity analysis is a method based on previously published empirical bone material property equations and on composite beam theory, which considers the elemental material composition of the vertebra and the geometry of the structure. Quantitative assessment of vertebral volumetric BMD through QCT, together with size, location, and geometry of the vertebral defect caused by the metastatic tumor, can more accurately predict, through composite beam theory, the vertebra's failure load.^7,11–13

We have developed an automated and user-friendly Spine Cancer Assessment (SCA) image-based analysis method that builds on a platform designed for clinical practice, with a workflow format that allows for rapid selection of patient computed tomography (CT) scans. The image-based analysis method implements composite beam theory and QCT and provides a report of the predicted failure load of the selected vertebral body. In addition, it facilitates prophylactic planning and analysis of treated vertebrae.

The aims of this study were to (1) validate the SCA image-based analysis method by correlating predictive fracture loads with experimentally measured values on fresh-frozen human cadaveric metastatic spine models and (2) evaluate the planning capabilities of the image analysis for vertebroplasty procedures. A previous study by Dragomir-Daescu et al.¹⁴ showed strength estimations obtained from quantitative computed tomography-based finite element models (QCT/FEA) to be dependent on CT scanner settings. For this purpose, we also aimed to (3) evaluate the effect of CT acquisition protocols on predicted failure loads.

Materials and Methods

Specimen selection

Three fresh-frozen cadavers were obtained from the anatomy department of Mayo Clinic after receiving study approval from the Mayo Clinic Research Biospecimens Subcommittee. The spines were dissected and wrapped in saline-soaked gauze, sealed in plastic bags, and stored at −20°C until further use.

Metastatic lytic defect model

Twenty-one vertebral bodies from three cadaveric thoracolumbar spines (T2-L5) were randomly divided into two groups: (1) simulated defect without treatment (negative control, n = 9) and (2) simulated defect with treatment (copolymer, n = 12). Metastatic models were created as previously described.¹⁵ Briefly, for the negative control and copolymer groups, ∼25% of the volume of the vertebral trabecular body was removed from the center core of the vertebrae. An in situ polymerizing formulation, consisting of poly(propylene fumarate) and poly(caprolactone) in a 1:1 ratio, was injected into the vertebrae in the treated defect (copolymer) group. The copolymer mix [P(PF-co-CL)] was synthesized as previously described.¹⁶ After defects were filled, the cadaveric spines were wrapped in saline-soaked gauze, sealed in a plastic bag, and stored at 4°C for 24 h to allow further polymerization without significant specimen degradation.

QCT scanning and biomechanical testing

After defect filling, cadaveric spines were scanned using a Siemens Somatom Definition CT scanner (Siemens, Malvern, PA) at 120 kVp and 400 mA. The spines were scanned over a calibration phantom (Midways, Inc., San Francisco, CA) containing five rods of reference materials, facilitating conversion of Hounsfield unit (HU) values from the CT images to K₂HPO₄ density (g/cm³) as a surrogate for BMD. Table 1 shows the specifications of the calibration phantom as specified by the manufacturer. Conversion of HU to BMD has been previously described in detail.¹⁷ To test the effect of imaging protocols on the predicted results, the scans were reconstructed with two different algorithms (B30 and B70, commonly used in clinical settings) with an in-plane resolution of 0.43 mm and a slice thickness of 0.6 mm.

Table 1.

Composition of Solid Reference Material in Calibration Phantom

Reference rod	H2O density	K2HPO4 density
1	1012.2 ± 2.3	−51.8 ± 0.1
2	1057.0 ± 1.9	−53.4 ± 0.1
3	1103.6 ± 1.7	58.9 ± 0.1
4	1119.5 ± 1.8	157.0 ± 0.3
5	923.2 ± 2.1	375.8 ± 0.9

After imaging, individual vertebrae were dissected from the cadaveric spines and stripped of soft tissue to prepare for mechanical testing as previously described.¹⁵ Briefly, posterior processes and intervertebral discs were removed, and the top and bottom regions of each vertebra were embedded in poly(methyl methacrylate) (PMMA) to ensure uniform loading during compression testing. Vertebral bodies were compressed to failure between aluminum platens using a material testing system (MTS 858 Mini Bionix, Eden Prairie, MN) at a rate of 5 mm/min. Force–displacement data were recorded at a rate of 102.4 Hz.^15,18 Failure was signaled by a sudden drop in the force–displacement curve, and failure load was measured as the first decrease in the force versus displacement curve.

Failure load prediction and prophylactic intervention

Digital Imaging and Communications in Medicine (DICOM) images obtained during the scanning process were saved to a local image database and imported into the SCA image-based method for analysis. The method for failure load prediction is discussed below, and a flow chart with an overview of the process is shown in Figure 1.

FIG. 1.

Overview of the failure load prediction process. DICOM images were imported to the SCA image-based analysis method. Vertebrae were selected and defined in the sagittal and coronal planes to cover the entire vertebral body height. An ROI was defined on the lytic lesion and a Young's modulus value was assigned based on the material within the defect (negative control or copolymer). After defining the lesion, an oval mask was placed on the vertebra of interest and analyzed for fracture characteristics. DICOM, digital imaging and communications in medicine; ROI, region of interest; SCA, spine cancer assessment.

Vertebra and lesion definition

The vertebra of interest was selected, identified in the CT image, and manipulated in all three CT scanning planes (Fig. 2). Briefly, identifiers were placed on the vertebra. In the sagittal plane, identifiers were placed on the top and bottom of the vertebral endplates. An additional identifier was then placed in the coronal plane to cover the entire vertebral body. This process was repeated for all vertebrae of interest. The phantom used during scanning was selected as the input parameter for the analysis.

FIG. 2.

(A) Vertebral bodies were selected for analysis (green highlight shows the selected vertebral body; blue highlight shows an already defined vertebral body). (B) Two lines were placed on the sagittal and coronal planes to define the vertebral body range and size. (C) A three-dimensional ROI was delineated that corresponded to the lytic lesion. The ROI can be visualized in all three planes. Color images available online at www.liebertpub.com/tec

A region of interest (ROI) was placed at the lytic region by outlining the defect on CT slices and assigning specific material properties (i.e., negative control or copolymer). Depending on the augmentation material used, a lesion could be assigned different Young's modulus values to represent various prophylactic interventions. In many cases, the selected vertebrae in the CT images were adequately aligned, but in some with abnormal spine curvature and vertebral axial rotation, these vertebrae in the images were realigned to improve visualization.

Mask placement and surgical planning

To prepare each vertebra for analysis, an elliptical ROI was placed to cover the entire vertebral body while excluding the posterior processes. The images were visualized in the axial plane to assure that the placement of the ellipse was adequate and covered the entire vertebra. The process of lesion definition and mask placement was repeated for surgical planning.

To virtually plan for prophylactic intervention, the vertebrae in the negative control group, with an empty lesion, were selected for failure load prediction using two different augmentation procedures, PMMA and copolymer. The ROIs previously established around the lytic defect were assigned simulated Young's modulus values corresponding to PMMA (2500 MPa) or copolymer (70 MPa).¹⁸ The ratio of increased failure loads for each condition was calculated as follows:

Failure analysis

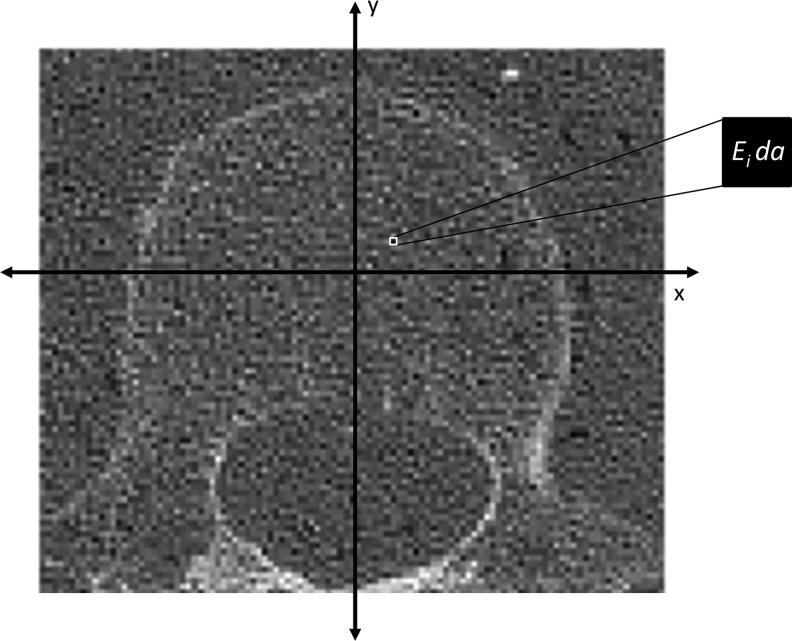
Axial rigidity (EA) was defined by the product of the material modulus (E) ([Pa]), obtained from the conversion of HU values to BMD, and from the cross-sectional area of the bone, as described in Equation (2):

where da corresponds to the pixel area (Fig. 3). Young's modulus was related to BMD according to Equation (3)¹⁹:

FIG. 3.

Schematic of analysis used in the SCA image-based analysis method. Hounsfield unit values in the image were converted to BMD based on a linear relationship obtained from the calibration phantom. A Young's modulus value (E [MPa]) was assigned to each voxel based on a density-dependent elastic modulus relationship previously established [Eq. (3)]. da corresponds to the pixel dimensions. BMD, bone mineral density.

Each vertebra was automatically processed in a slice-by-slice manner from the superior endplate to the inferior endplate. Aggregate data were generated for each vertebra, with single measurements taken at 0% to 100% of the vertebra height in 5% increments. Failure load of the vertebra was determined from the cross section with the lowest axial rigidity and was calculated as follows²⁰:

Statistical analysis

Pearson correlation analysis was used to assess the strength and directionality between predicted and experimentally measured failure loads. Significance was set at p ≤ 0.05.

Results

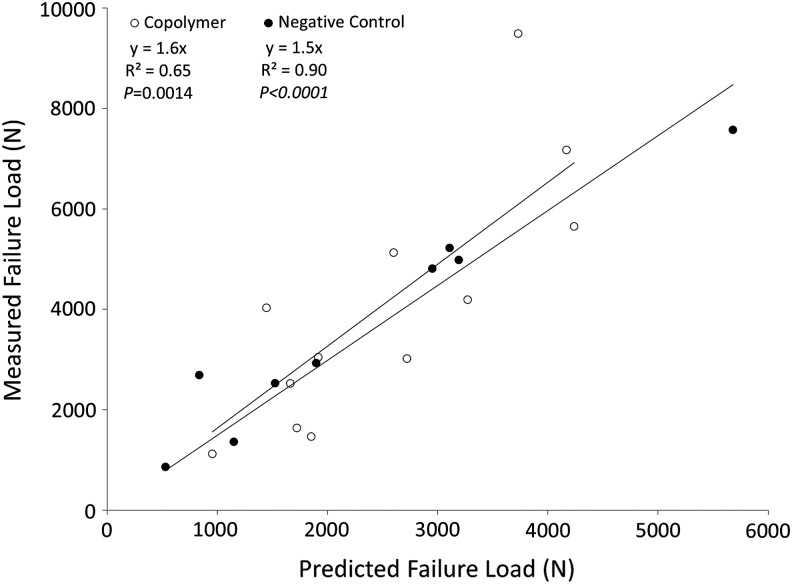
Simulated lytic defects were successfully created in the cadaveric spines. Measured versus predicted failure loads for all specimens are shown in Figure 4. The predicted loads correlated well with the outcomes observed experimentally (R² = 0.73, p < 0.0001; y = 1.6x). Predicted outcomes for the copolymer and negative control groups are shown in Figure 5. The copolymer predictions had a correlation of R² = 0.65 (p = 0.0014), whereas the predictions from the negative control specimens were highly correlated with the measured values (R² = 0.90, p < 0.0001).

FIG. 4.

Measured versus predicted failure load for all data (negative control and copolymer vertebrae).

FIG. 5.

Measured versus predicted failure load for the copolymer and negative control samples.

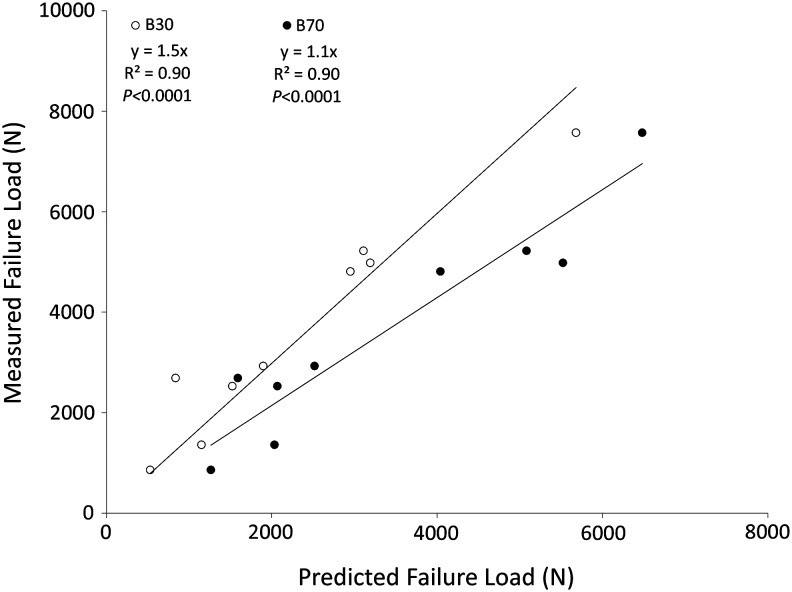
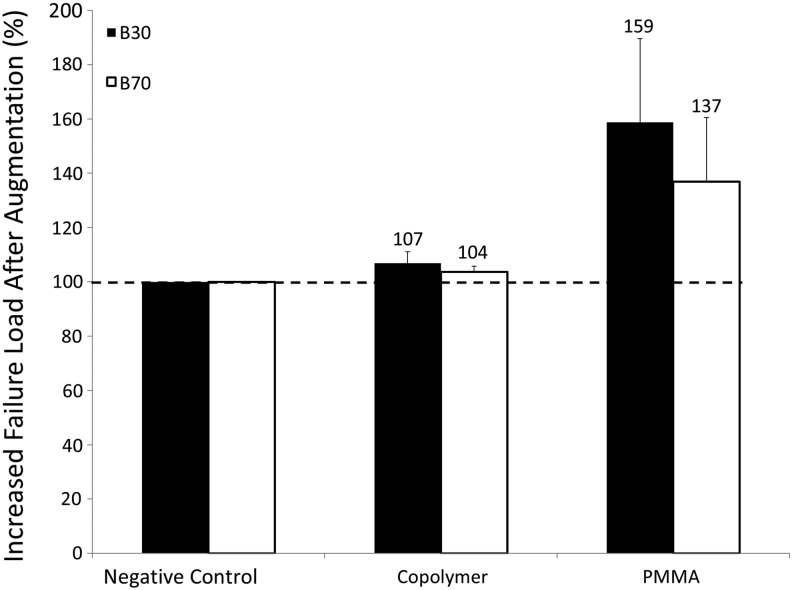
To test the effect of scanning protocols on the predictive power of the process, the negative control specimens were analyzed using two reconstruction algorithms. A similar correlation was obtained for both reconstruction algorithms (R² = 0.9 (p < 0.0001), y = 1.5x, smooth kernel [B30]; R² = 0.9 (p < 0.0001), y = 1.1x, sharp kernel [B70]). However, the smooth algorithm tended to underestimate predicted failure loads by ∼50% compared with the ∼10% underestimate of the sharp kernel (Fig. 6). The percent increase in failure loads after prophylactic vertebroplasty is shown in Figure 7. Because of the lower Young's modulus value used for the copolymer in virtual planning, the PMMA showed a higher increase in predicted failure loads.

FIG. 6.

Measured versus predicted failure load for the negative control samples analyzed with two different computed tomographic reconstruction algorithms (B30 [smooth kernel] and B70 [sharp kernel]).

FIG. 7.

The spine cancer assessment image-based analysis method was used to calculate failure loads after virtually augmenting the negative control samples with two polymers, a copolymer or PMMA. Failure loads of the augmented vertebrae were analyzed using two computed tomographic reconstruction algorithms (B30 [smooth kernel] and B70 [sharp kernel]). PMMA, poly(methyl methacrylate).

Discussion

We have developed a method that allows noninvasive prediction of the vertebrae's failure load as well as surgical planning of prophylactic vertebroplasty procedures. The study showed good correlation between the predicted loads and the outcomes observed experimentally. The predicted outcomes for the copolymer group showed good correlation (R² = 0.65) with experimentally observed values, whereas predictions from the negative control specimens were highly correlated with measured outcomes (R² = 0.90). Furthermore, the type of scanning protocol used strongly affected the predictive power of the process, although the correlation was not affected. Scanning protocols were previously shown to affect estimated BMD values obtained from HUs from CT images.¹⁷ Because the empirical material equation used in the study relates HUs to BMD to Young's modulus, any differences in the estimation of BMD values from CT scanning protocols will highly influence the predicted fracture loads of the vertebrae.

The skeleton is the third most common site of metastatic cancer, accounting for almost half of all cancer metastases.⁴ Cancers such as lymphoma, melanoma, carcinoma of the breast, and those affecting the prostate, kidney, and lung account for 75% of spinal metastases.²¹ Currently, patients with cancer who present with spine metastasis undergo subjective fracture risk assessment by the clinician. However, these assessments, which might eventually lead to reconstructive surgery or other conservative treatment, are based on clinical and radiographic guidelines that are not validated and have been demonstrated to lead to an incorrect prediction of fracture.²²

Traditionally, lesion size and geometry (determined by plain radiographs) have been used as predictors of vertebral fracture risk, but lesion size accounts for ∼50% of the variation in vertebral failure load.^23,24 To visually detect a lesion on a radiograph, a defect must affect 50% to 75% of the vertebral body, which reduces vertebral strength by ∼50% to 90%.⁷ Furthermore, defect size is not an adequate parameter for predicting vertebral failure because structural behavior also depends on the cross-sectional geometry, microarchitecture, and material properties of the bone.

In this report, we describe a noninvasive tool that characterizes and predicts failure load of vertebral bodies with lytic defects and vertebral bodies treated with prophylactic procedures. Furthermore, the process used can facilitate analysis of vertebrae with defects and planning of various treatment options for fracture prevention. In addition, we investigated the effect of different CT scanning protocols on failure load predictions. As shown, the reconstruction algorithms (B30 vs. B70) used in the scanning acquisition protocol will affect predicted fracture load values. This is due to the HU values in the CT reconstructed images associated with both reconstruction algorithms, eventually yielding different Young's modulus [E] values and predicted failure loads. Although the linear relationship between measured versus predicted failure loads differs in both reconstructions, we have shown good correlations with both. However, this shows the importance of the image scanning parameters in the predicted outcomes and demonstrates that patient failure loads predicted using this process will be dependent on the reconstruction method. If a fracture risk analysis is to be performed, a specific set of validated scanning parameters needs to be implemented during imaging. However, if images are obtained with a different set of scanning and reconstruction inputs (other than the ones specified in this study), a validation would have to be performed to obtain a correlation between measured and predicted values.

Several studies have investigated the potential of axial rigidity analysis on the estimation and prediction of failure loads of bones from CT images.^{7,11,12,21,25,26} Windhagen et al.²⁶ calculated the axial rigidity of thoracic vertebrae and showed a high correlation between predicted and measured failure loads. Hong et al.¹² conducted an ex vivo study analyzing QCT images of trabecular bone obtained from whale vertebrae. Their findings indicated that the load-bearing capacity of the trabecular core was directly proportional to the axial rigidity at the weakest cross section. Similarly, Damron et al.¹¹ and Snyder et al.⁷ evaluated the performance of axial rigidity analysis on pathologic femoral fractures and on vertebrae of women with breast cancer and spinal metastasis, respectively. The results showed that CT-based structural rigidity analysis was better than current guidelines for predicting femoral fractures and it was as sensitive as and more specific than current radiographic criteria for predicting vertebral failure in patients with spine metastasis. However, the image-based method of structural analysis developed by those researchers requires an experienced biomedical engineer for the analysis. In addition, the process currently used for QCT or axial rigidity analysis includes additional data visualization software, and such software might be poorly suited for translation to a clinical setting.

We strongly believe that the validated and quantitative results obtained from the analysis described in the current study could help improve fracture prediction in the clinical setting. The SCA program is a robust image-based analysis method that is built on a platform designed for clinical practice and is able to appropriately accommodate current clinical CT images and files. It allows rapid selection of patient CT exams, followed by guided image analysis predicting failure characteristics of the vertebrae. In addition, our SCA image-based analysis method allowed for planning of prophylactic procedures and visualization of the predicted fracture characteristics of the vertebrae upon augmentation.

We note several limitations to the current study. First, although the analysis appropriately predicted failure loads of the vertebrae, further studies should be conducted to increase the number of specimens with lytic lesions. Second, vertebrae augmented with copolymer showed a lower correlation when compared with the negative control samples. Although the procedure was able to account for the analysis of experimentally augmented vertebrae, the process is user dependent because the ROI outlining the defect is defined by the operator. The spreading of the polymer into the trabecular structure adds uncertainties to the analysis and selection of the ROI. Consequently, an incorrect material property (Young's modulus) value might be assigned to the polymer not chosen in the ROI or to the cancellous bone defined within the ROI. Results of this process will eventually lead to a lower correlation coefficient, as we observed in the copolymer group and the pooled data. Future sensitivity studies should also be performed to investigate user dependency and input in each step of the process. Furthermore, incomplete filling of the lesion in the cadaveric vertebrae with the polymer can lead to air bubbles in the ROI compared with the image model (which is always perfectly filled). With uncontrolled delivery and distribution of augmentation materials in the vertebrae, although the planning process allows for varying materials to be evaluated, the filling process might potentially lead to different results than those predicted. However, the process showed high correlation between the failure loads of vertebrae with lytic lesions and the measured experimental values.

Although the image-based method allows for bending rigidity analysis, an additional validation procedure should be conducted to determine the correlation between predicted and observed outcomes. Fourth, this process does not consider the effect of the posterior processes and the intervertebral discs. In vivo situations might differ from the predicted scenario because of the fracture-preventing compensatory mechanisms imposed by the posterior bones and soft tissues such as ligaments, discs, and muscle. However, contrary to current qualitative predictive tools and methods, which also do not account for the effect of soft tissue on fracture, we believe that the proposed image-based method for fracture load prediction, providing a quantitative measure of fracture load, together with planning for varying augmentation procedures, can provide a more reliable guideline for fracture risk in the clinical setting. Finally, the predicted loads obtained in this process are dependent on the material equation used, relating HU values from the CT images to Young's modulus (E) [Eq. (3)]. There exist several equations relating HU to E, depending on the type of bone (tibia, femur, vertebra) and investigators.^9,27 Equation (3) is a widely used and accepted empirical linear equation associating HU and E for vertebra. Its implementation in our CT-based image analysis yielded good correlations for the pooled and individual group data. It is important to note that the application of a different equation relating HU and E from vertebra in our methodology would have potentially yielded different predicted failure loads to the ones observed in this study, requiring an additional validation of the process.

Conclusion

The SCA image-based analysis method was able to calculate the failure loads from QCT scans in vertebrae with simulated metastatic lytic defects, with or without treatment, facilitating clinical applicability and providing more reliable guidelines for physicians to select appropriate treatment options. It was validated by experimental methods showing high correlations for all pooled specimens and a higher correlation for the untreated vertebrae with lytic defects. Differences in predicted outcomes were also observed with varying CT acquisition protocols. Furthermore, the process could accommodate augmentation planning procedures that aim to determine the optimum biomaterial that would increase the vertebral body failure load while not increasing it to the level of a lytic vertebra augmented with PMMA, which creates a stiffness mismatch in the spine potentially leading to adjacent vertebral fracture and disc degeneration.

Acknowledgments

This work was supported by the National Institutes of Health grant R01 AR056212. The authors also acknowledge the National Institute of Arthritis and Musculoskeletal and Skin Diseases for the Musculoskeletal Research Training Program T32-AR56950. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Disclosure Statement

No competing financial interests exist.