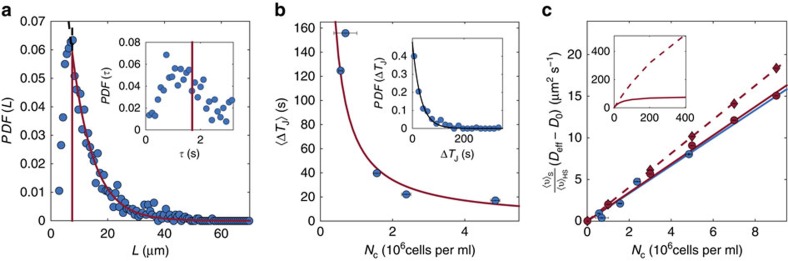
Figure 3. Microscopic characterization of particle dynamics.

(a) Probability distribution function (PDF) of the end-to-end length L of the jumps. Above L_T=7.5 μm, the distribution is well fitted by an exponential function with characteristic length L_J=7.5 μm (solid red line). Inset: PDF of the duration 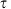of the jumps. The average is 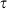=1.7 s when considering only jumps of length L≥L_T (solid red line). (b) Mean time interval between consecutive jumps, 〈ΔT_J〉, as a function of N_c. The red solid line is the hyperbolic fit used in the simulations, 〈ΔT_J〉=((68.2±8)/N_c)s (N_c in units of 10⁶cells ml⁻¹). Horizontal error bars are the standard deviations of cell concentrations. Inset: PDF of the time interval ΔT_J between consecutive jumps at N_c=(1.56±0.10) × 10⁶ cells ml⁻¹. Black solid line: exponential fit with characteristic time (31.9±4)s. Note that these distributions provide a biased measure of the mean waiting time 〈ΔT_J〉, which should be estimated instead from the average number of jump events as discussed in Supplementary Methods 4. (c) Effective diffusivities, D_eff−D₀, from the Hele–Shaw experiment (blue circles) and from the simulations: red circles/solid red line for 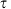=1.7 s (slope 1.03 × α_HS); red diamonds/dashed red line for 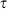=0.1 s (slope 1.22 × α_HS). Vertical error bars represent the uncertainty on the fits to obtain the effective diffusivities. Horizontal error bars are the standard deviations of the cell concentrations. Inset: continuation of the simulated D_eff−D₀ curves to very high cell concentrations shows saturation to a 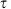-dependent value.