Identifying a maximum tolerated contour in two-dimensional dose-finding

Abstract

The majority of Phase I methods for multi-agent trials have focused on identifying a single maximum tolerated dose combination (MTDC) among those being investigated. Some published methods in the area have been based on the notion that there is no unique MTDC, and that the set of dose combinations with acceptable toxicity forms an equivalence contour in two dimensions. Therefore, it may be of interest to find multiple MTDC's for further testing for efficacy in a Phase II setting. In this paper, we present a new dose-finding method that extends the continual reassessment method to account for the location of multiple MTDC's. Operating characteristics are demonstrated through simulation studies, and are compared to existing methodology. Some brief discussion of implementation and available software is also provided.

1. Motivation

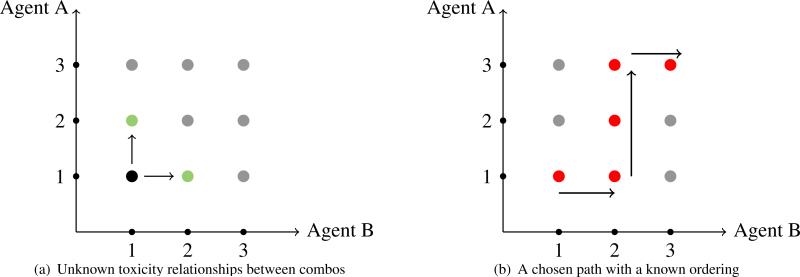
In oncology drug development, there has been an increasing interest in investigating the potential of drug combinations for patient treatment. The motivation to treat with drug combinations stems from the desire to improve the response of the patient, especially those who have been resistant to traditional treatment. Multi-agent dose-finding trials present the significant challenge of finding a maximum tolerated dose combination (MTDC), or combinations, of the agents being tested with the typically small sample sizes involved in phase I studies. The complexity of combining more than one agent renders many single-agent dose-finding methods useless. A key assumption to phase I methods for single-agent trials is the monotonicity of the dose-toxicity curve, which lends itself to escalation along a single line of doses. Given the severity of a toxic response (dose-limiting toxicity; DLT yes/no) for a particular patient, we either recommend the same dose for the next patient or move to one of two adjacent doses (i.e. either escalate one dose higher or de-escalate to one dose lower). In studies testing combinations, there will most likely be more than one possible dose pair to consider when deciding on which combination to enroll the next patient cohort. For instance, suppose a cohort of patients receives a combination consisting of the lowest dose of each drug and it is well-tolerated. It is not clear which dose pair should be assigned to the next cohort of patients, as illustrated in Figure 1 (a). The toxicity ordering is usually unknown between combinations located on the same diagonal of the drug combination matrix.

Figure 1.

Illustration of a drug combination matrix and the unknown toxicity relationships between off-diagonal elements. Often a single path with a known ordering is chosen to explore.

A traditional approach to this problem is to pre-select combinations with a known toxicity order, and apply a single-agent design by escalating and de-escalating along a chosen path as in Figure 1 (b). This approach transforms the two-dimensional dose-finding space into a one-dimensional space, and was the approach taken in much of the early work done in combinations. Korn and Simon [1] present a graphical method, called the “tolerable dose diagram,” based on single agent toxicity profiles, for guiding the escalation strategy in combination. Kramar, Lebecq and Candahl [2] also lay out an a priori ordering for the combinations, and estimate the MTDC using a parametric model for the probability of a DLT as a function of the doses of the two agents in combination. The disadvantage of this approach is that it limits the number of combinations that can be considered and it can potentially miss promising dose combinations located outside of the chosen path.

More recent methods have moved away from reducing the two-dimensional dose-finding space to a single dimension, a thorough review of which is given in Harrington et al. [3]. Since the publication of Harrington et al. [3], several new methods have been proposed [4, 5, 6, 7, 8]. The primary focus of these methods has been to find a single MTDC for recommendation in Phase II studies. However, another significant challenge of combination studies is that multiple “equivalent” MTDC's may exist, forming a maximum tolerated contour (MTC) in the two-dimensional space. To this end, Thall et al. [9] proposed a six-parameter model for the toxicity probabilities in identifying a toxicity equivalence contour for the combinations. Ivanova and Wang [10] applied bivariate istonic regression to estimate the MTC in drug combination studies. A recent editorial in Journal of Clinical Oncology by Mandrekar [11] described the use of the method of Ivanova and Wang [10] in a real Phase I study aiming to identify multiple MTDC's [12]. Wang and Ivanova [13] proposed a logistic-type regression that used the doses of the two agents as the covariates. A sequential continual reassessment method (CRM; [14]) for selecting multple MTDC's was described by Yuan and Yin [15]. Tighiouart, Piantidosi, and Rogatko [16] proposed a Bayesian adaptive dose-finding method that extends escalation with overdose control (EWOC,[17]) in order to estimate the MTC with continuous dose levels. Mander and Sweeting [18] published a curve-free method that relies on the product of independent beta probabilities for determining a MTC.

In this paper, we describe a new method for identifying a MTC in two-dimensional dose-finding studies. The manuscript is organized as follows. In Section 2, the general considerations and overall strategy in estimating the MTC are discussed. In Sections 3 and 4, proposed methodology and a dose-finding algorithm for identifying an equivalence contour are described. Operating characteristics, including a single-trial illustration and simulation results, are provided in Section 5. Finally, Section 6 contains some concluding remarks and discussion.

2. General considerations

2.1. Example with two rows

In general, we consider two-agent combination trials to be testing agents A and B with dose levels i = 1, . . . , I for A and j = 1, . . . , J for B, resulting in a I × J dose combination matrix. Let d_ij denote the combination consisting of dose level i of agent A and dose level j of agent B, and denote the probability of dose-limiting toxicity (DLT) at d_ij with π(d_ij) and the target toxicity rate (TTR) specified by physicians by ϕ. As in Ivanova and Wang [10], we focus on the most common cases in which A has a small number of levels, with I typically being equal to 2 or 3. As a motivating example, consider a phase I trial that is currently open to accrual at the University of Virginia Cancer Center. The trial is testing the combination of two oral targeted inhibitors (Agents A and B) in patients with relapsed or refractory mantle cell lymphoma. The study is investigating the combination of 2 doses (200 and 400 mg) of Agent A; A₁ < A₂, and 4 doses (140, 280, 420, 560 mg) of Agent B; B₁ < B₂ < B₃ < B₄. Based on initial discussions with clinicians, the primary objective of the study was to determine an MTDC for each of the 2 doses (200 and 400 mg) of Agent A. We use this 2 × 4 example to illustrate the proposed method, which can easily be generalized to problems of other dimensions (i.e. number of dose levels).

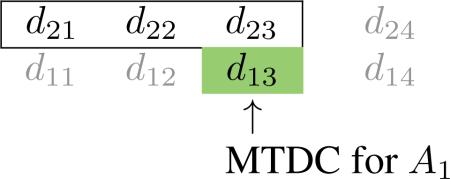
A reasonable assumption to be made is that toxicity increases monotonically with the dose of each agent, if the dose of the other agent is held fixed (i.e., across rows and up columns of Table 1). If Agent B is fixed at dose level j, then we assume that π(d_ij) < π(d_i′j) whenever i < i′. In other words, for each level, j, of Agent B (i.e. within each column), the probability of DLT is monotonically increasing so that π(d_1j) < π(d_2j) < · · · < π(d_Ij). Similarly, for each level, i, of Agent A (i.e. within each row), the probability of DLT is monotonically increasing so that π(d_i1) < π(d_i2) < · · · < π(d_iJ). It is expected that doses in each row of the drug combination matrix will have DLT probabilities at least as high as those in rows below. Therefore, the estimated MTDC for row i should be the same as or lower than the estimated MTDC for row i′ whenever i > i′. The goal is to find an MTDC for each dose of Agent A by locating j* ∈ {1, . . ., 4} such that d_ij* has DLT probability closest to the rate ϕ for each i(i = 1,2); i.e. find an MTDC in each row i such that

$$d_{i{j}^{\ast }}=\arg \underset{j}{\min }\mid \pi \left(d_{ij}\right)-\varphi \mid .$$

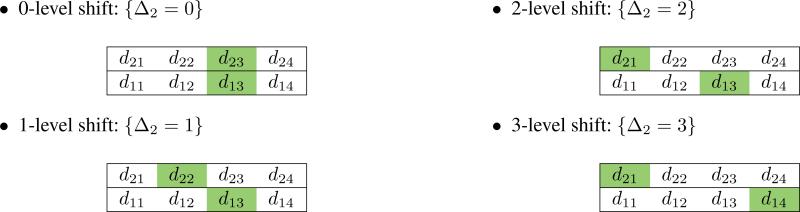
If the MTDC in row i = 1 is estimated to be d_1j*, then the estimated MTDC in row i = 2 will be shifted Δ₂ levels away from d_1j* so that the MTDC in row 2 is d_2j* – Δ₂; Δ₂ ∈ {0, 1, 2, 3} with the restriction j* > Δ₂. Row 1 has at least the most toxic MTDC the MTDC in row 1 will contain at least the largest dose of Agent B). For instance, suppose MTDC in row 1 is estimated to be d₁₃. If dose of A is fixed at A₂, the estimated MTDC of drug B must be lower than or equal to 3 (i.e. B₁, B₂, or B₃), as illustrated in the following.

Table 1.

Treatment labels for a 2 × 4 drug-combination matrix

		Doses of B (mg)
		140	280	420	560
Doses of A (mg)	400	d 21	d 22	d 23	d 24
	200	d 11	d 12	d 13	d 14

The truth could be any one of the four possible values for Δ₂, and we want to account for this uncertainty in the design by using the data to estimate the relative location of the MTDC between rows. A similar strategy has been implemented in designs that account for patient heterogeneity [19, 20]. The relative location of the MTDC between rows can be illustrated as follows.

2.2. Extension to more than two rows

The expressions above can easily be extended to drug combination matrices with more than two rows and more than four dose levels. If the estimated MTDC for A₁ is d_1j*, then the estimated MTDC for A_i is d_ij* – Δ_i. The possible shifts between rows is now represented by multiple Δ values {Δ₂, Δ₃, . . . , Δ_I}, where Δ₂ ≤ Δ₃ ≤ · · · ≤ Δ_I. For instance,

• 2-level shift between rows 1 and 2; 3-level shift between rows 1 and 3: {Δ₂ = 2, Δ₃ = 3}.

The possible row relationships illustrated in this section can be more formally expressed in probability models to be utilized in estimating the combination-toxicity curve.

3. Proposed method

3.1. Working probability models

The proposed method is based on utilizing a class of working models that correspond to relative locations (shifts) of the MTDC in each row of the matrix. Let M_k denote the working probability model associated with kth set of Δ values. Throughout the trial of N patients, we sequentially observe {(X_n, Y_n); n = 1, . . . , N}, where X_n = x_n denotes the combination assigned to patient n and Y_n = y_n is a binary toxicity indicator (DLT; yes/no) for the nth patient. The combination x_n takes values from the discrete set {d_ij; i = 1, . . . , I; j = 1 . . . , J}. Under working model M_k, the true toxicity probability at combination x_n = d_ij is approximated by a class of one-parameter models, F, so that

$$\pi \left(x_n\right)=\mathrm{Pr}(Y_n=1\mid X_n=x_n)=\mathbb{E}(Y_n\mid x_n)\approx F_k(x_n,\theta )$$

for some parameter θ ∈ Θ common to all working models. We could choose from a number of working models that are common to the CRM class of models [21], such as power model, hyperbolic tangent function, or a one-parameter logistic model. As an illustration, consider the 2 × 4 grid from the example in Section 2.1. Each of the K = 4 possible Δ₂ ∈ {0, 1, 2, 3} values above correspond to a candidate model M_k. Suppose that we choose the power model

$$F_k(d_{ij},\theta )={\left[p_k\left(d_{ij}\right)\right]}^{\exp \left(\theta \right)},$$

such that Θ = (−∞, ∞) and suppose that the target toxicity rate is ϕ = 0.30. For each of the contending models, we begin by choosing skeleton values, p_k(d_1j), in row 1, and proceed by “shifting” the skeleton in row 2 to correspond to the Δ₂ value of that particular model.

The overall strategy is to use model selection techniques to sequentially choose the working model most consistent with the data in order to guide allocation decisions throughout the trial. Of course the skeletons above can be chosen in a number of ways that respect the structure of the shift model described in Section 2. In the Supporting Web Materials, we investigate the impact of various skeletons on the performance of our method.

3.2. Likelihood and inference

We let the plausibility of each working model be expressed through a set of prior weights P = {P(M₁), . . . , P(M_K)}, where P(M_k) ≥ 0 and Σ P(M_k) = 1; k = 1, . . . , K. Even when there is no prior information available on the contending working models, we can formally proceed in the same manner by specifying a discrete uniform prior for P. Using the accumulated data, {(x₁, y₁), . . . , (x_n, y_n)}, from the first n accrued patients, we derive maximum likelihood estimates (MLE's) under each of the contending models by maximizing the likelihood

$$L_{nk}\left(\theta \right)=\prod _{\ell =1}^n{\left\{F_k(x_{\ell },\theta )\right\}}^{y_{\ell }}{\{1-F_k(x_{\ell },\theta )\}}^{(1-y_{\ell })}$$

under each working model M_k. We rely on model selection techniques to identify the best-fitting model among the candidates. For instance, we implement the commonly used Akaike [22] information criterion for model k, which takes the form

$${\mathrm{AIC}}_{nk}=-2\log L_{nk}\left({\widehat{\theta }}_{nk}\right)+2\nu ,$$

where $L_{nk}\left({\widehat{\theta }}_{nk}\right)$ is the value of the likelihood function evaluated at its MLE of the parameter θ, and ν is the number of model parameters, which, in the particular case considered here, takes a value of ν = 1 for every model. We seek weights that can be associated with each model, and implement the smoothed AIC estimator [23]

$$w_{nk}=\frac{P\left(M_k\right)\exp (-{\mathrm{AIC}}_{nk}∕2)}{\sum _{k=1}^{K}P\left(M_k\right)\exp (-{\mathrm{AIC}}_{nk}∕2)}.$$

We appeal to sequential model choice to inform our decision making. The model weights are adaptively updated by the data after each cohort inclusion, which is indicated by the subscript n in the preceding expressions. When a new cohort of patients is to be accrued to the study, we choose a single model, M_h, with the largest model weight such that

$$h=\arg \underset{k}{\max }{w}_{nk},k=1,\dots ,K.$$

We then utilize the h th working model, F_h(d_ij, θ), to generate DLT probability estimates at each combination such that

$$\widehat{\pi }\left(d_{ij}\right)=F_h(d_{ij},{\widehat{\theta }}_{nh});{\widehat{\theta }}_{nh}=\arg \underset{\theta }{\max }{L}_{nh}\left(\theta \right),$$

which we use to direct allocation decisions reflected in the following dose-finding algorithm.

4. Dose-finding algorithm

4.1. Initial design

Within the framework of sequential likelihood estimation, an initial escalation scheme is needed, since the likelihood fails to have a solution on the interior of the parameter space unless some heterogeneity (i.e. at least one DLT and one non-DLT) in the responses has been observed. This is done by specifying an initial design of a predetermined combination sequence, {x_1,0, . . . , x_N,0}, to follow until the occurrence of the first DLT, before switching to the modeling stage. The initial design essentially amounts to pre-specifying a path within the drug combination matrix to adhere to in order to get the trial underway. This could, of course, be done in several ways, and could possibly include some randomization if more than one combination could be considered for escalation, as is often the case in drug combination studies. In this work, we choose to begin the trial by allocating along the bottom row, and, in the absence of DLT along a row, continuing to escalate moving up the rows of the grid. This would create an initial sequence of x = {x_1,0 = d₁₁, x_2,0 = d₁₂, x_3,0 = d₁₃, . . . , x_N,0 = d_IJ}. The other component to the initial design that must be specified is the initial cohort size, c = {c_1,0, . . . , C_N,0}, at each combination. Based on the recommendations of Jia, Lee, and Cheung [24], we want to avoid an overly conservative initial design that treats too many patients at sub-optimal combinations. Therefore, we specify an initial cohort size of c_n,0 = 1 for all combinations in x. Allocation continues according to {x_1,0, c_1,0), . . . , (x_N0, c_N,0)} until a DLT is observed or until the maximum sample size N has been reached. Subsequent to a DLT being observed, the design proceeds to model-based allocation.

4.2. Model-based allocation

After each single patient cohort inclusion,

1. Based on the accumulated data from n patients {(x₁, y₁), . . . ,(x_n, y_n)}, use sequential model selection to choose working model most consistent with data

2. According to chosen working model, update the estimated DLT probabilities $\widehat{\pi }\left(d_{ij}\right)$ for all combinations

3. In each row, i, locate j* ∈ {1, . . . , J} such that d_ij* has estimated DLT probability, $\widehat{\pi }\left(d_{ij}\right)$, closest to target rate ϕ so that.

   $$d_{i{j}^{\ast }}=\arg \underset{j}{\min }\mid \widehat{\pi }\left(d_{ij}\right)-\varphi \mid$$

4. Create a set, $S=\{d_{1j_1^{\ast }},\dots ,d_{I{j}_I^{\ast }}\}$, of recommended combinations in each row i, and randomize next patient to treatment in S with equal probability.

5. The MTC is formed by the set S after the inclusion of the prespecified, maximum sample size of N patients.

5. Operating characteristics

5.1. Illustration

In this section, we illustrate the behavior of the method described in this article under a set of true DLT probabilities for the 2 × 4 example described in Section 2.1. The TTR is set to ϕ = 0.30, and the total sample size is N = 30 patients. The true DLT probabilities, π(d_1j), for row 1 are {0.07, 0.14, 0.22, 0.31} , indicating that dose level 4 (i.e. d₁₄) is MTDC in row 1. For row 2, the true probabilities are {0.11, 0.20, 0.29, 0.40}, indicating that dose level 3 (d₂₃) is the MTDC in row 2. The set S = {d₁₄, d₂₃} form the MTC, indicating that the model M₂ is most consistent with the true underlying DLT probabilities, coinciding with a true shift of Δ₂ = 1 level between the two rows. The method embodies characteristics of the CRM, so we appeal to its features in specifying design parameters. For instance, the skeleton values, p_k(d_ij), were chosen according to the algorithm of Lee and Cheung [25], and are reflected in the working models given in Section 3.1. We assumed that each model was equally likely at the beginning of the trial and set P(M_k) = 1/4; k = 1, . . . , 4.

The data from the entire simulated trial are provided in Table 2. The first 3 eligible patients are administered escalating combinations along row 1, and 0 DLT's are observed on d₁₁, d₁₂, and d₁₃. The first DLT occurs in patient 4 on combinations d₁₄, at which point the modeling stage begins. With this limited amount of data, M₄ is estimated to be the true shift model, and ${\widehat{\theta }}_{4,4=-0.305}$. These values are used to calculate DLT probability estimates in each row via $\widehat{\pi }\left(d_{ij}\right)\approx p_4{\left(d_{ij}\right)}^{\exp (-0.305)}$, yielding {0.03, 0.13, 0.26, 0.41} in row 1 and {0.41, 0.56, 0.68, 0.78} in row 2. Combinations S = {d₁₃ , d₂₁} are indicated to have an estimated toxicity rate closest to the TTR. Patient 5 is randomized with probability 1/2 to either d₁₃ or d₂₁, which yields a recommendation of d₁₃ for patient 7, on which he/she does not experience a DLT. The toxicity data are then updated, from which M₄ is estimated to be the true shift model, and ${\widehat{\theta }}_{5,4}=-0.111$. The updated DLT estimates become {0.02, 0.08, 0.19, 0.34} in row 1 and {0.34, 0.49, 0.62, 0.74} in row 2, indicating that a combination in S = {d₁₃, d₂₁} should be recommended. It is important to note that the DLT probabilities are updated in row 2, even though we have yet to observe a patient in this row, illustrating the formal borrowing of information across rows afforded by the model. This notion is also reflected towards the end of the trial when the last patient (pt # 29) treated in row 1 is recommended d₁₃, yet the final recommendation for this group is d₁₄ due to the data accumulated on the final patient in row 2. Overall, in this simulated trial (Table 2), N = 30 patients are treated, yielding MTDC recommendations S = {d₁₄, d₂₃} forming the equivalence contour.

Table 2.

Simulated sequential trial of N = 30 patients illustrating the proposed approach.

n	dij	yij	h	${\widehat{\theta }}_{nh}$	n	dij	yij	h	${\widehat{\theta }}_{nh}$
1	d 11	0	-	-	16	d 22	0	1	−0.234
2	d 12	0	-	-	17	d 22	0	1	−0.189
3	d 13	0	-	-	18	d 13	0	1	−0.134
4	d 14	1	4	−0.305	19	d 23	1	1	−0.226
5	d 13	0	4	−0.111	20	d 22	0	1	−0.188
6	d 21	1	4	−0.436	21	d 13	0	1	−0.141
7	d 21	0	4	−0.248	22	d 13	1	1	−0.220
8	d 13	1	4	−0.557	23	d 12	0	1	−0.187
9	d 21	0	3	−0.117	24	d 13	0	1	−0.145
10	d 21	0	2	−0.198	25	d 13	0	1	−0.107
11	d 13	1	2	−0.351	26	d 13	0	2	0.116
12	d 21	0	1	−0.478	27	d 22	0	1	−0.048
13	d 22	0	1	−0.404	28	d 13	0	2	0.172
14	d 22	0	1	−0.340	29	d 13	0	2	0.198
15	d 12	0	1	−0.284	30	d 23	1	2	0.222

Maximum tolerated contour (MTC): S = {d₁₄, d₂₃}

5.2. Simulation comparison with alternative method

We assessed performance of the proposed method based on 3 evaluation indices, and compared it to the method of Ivanova and Wang [10]. The operating characteristics among the two methods were compared by simulating 4000 trials under 6 toxicity scenarios (I–VI) of 3 × 6 and 2 × 6 dose combination matrices with varying positions of true MTDCs, as shown in Table 3. The TTR is set to ϕ = 0.20 in all scenarios, and the sample size is N = 54 in Scenarios I–III, and N = 36 in Scenarios IV–VI. We also investigated additional scenarios in which MTDC's were located at the far left and far right of the drug combination matrix. These additional results are reported in Supplemental Web Material Tables 11–13. Throughout the simulations studies, a cohort of size 1 is used for the proposed method. All true scenarios and results for the Ivanova and Wang method were taken from their paper. User friendly R code for simulating the proposed method can be found at http://www.faculty.virginia.edu/model-based_dose-finding/. In the specification our working models, we restrict Δ_i to be an element of the set {0, 1, 2, 3}, indicating that we don't allow for more than a 3 dose level shift between two adjacent rows of the matrix. We feel that these shifts represent the most common cases in practice. However, shifts of 4 or more are possible of course, and the proposed method has the ability to handle such possibilities by including more working models. We investigate the impact of allowing larger shifts and including more working models in Supporting Web Materials Tables 1 and 2. The candidate working models (skeletons) used in simulation are provided in Supplemental Web Material Tables 3–5.

Table 3.

Six scenarios of true toxicity probabilities for 3 × 6 (Scenarios I–III) and 2 × 6 (Scenarios IV–VI) drug combination matrices. The target toxicity rate is ϕ = 0.20 in each scenario. True maximum tolerated dose combinations are indicated in bold-type, and the set of maximum tolerated dose combinations forms a maximum tolerated contour. These scenarios orginally appeared in Ivanova and Wang [10]

Scenario		1	2	3	4	5	6
I	3	0.11	0.22	0.32	0.45	0.52	0.66
	2	0.07	0.12	0.23	0.40	0.48	0.58
	1	0.05	0.08	0.13	0.15	0.23	0.34
II	3	0.05	0.08	0.11	0.15	0.21	0.29
	2	0.04	0.06	0.09	0.13	0.18	0.25
	1	0.04	0.05	0.08	0.11	0.15	0.21
III	3	0.20	0.30	0.41	0.53	0.65	0.70
	2	0.10	0.20	0.25	0.32	0.41	0.50
	1	0.03	0.05	0.13	0.20	0.27	0.35
IV	2	0.08	0.13	0.20	0.29	0.40	0.52
	1	0.06	0.09	0.14	0.22	0.31	0.43
V	2	0.10	0.16	0.22	0.34	0.46	0.59
	1	0.04	0.06	0.10	0.15	0.22	0.32
VI	2	0.20	0.29	0.40	0.53	0.65	0.75
	1	0.13	0.20	0.29	0.40	0.53	0.65

In general, our goal is to evaluate (1) how well each method locates true MTDC's at and around the TTR in each row (percentage of correct recommendation; PCR), and (2) how well each method allocates patients to combinations at and around the TTR in each row (percentage of correct allocation; PCA). Of course, there will always be certain scenarios in which some methods perform better than others. Therefore, a useful tool in comparing dose-finding designs can be average performance over a broad range of scenarios. While traditional evaluation measures, such as the percentage of recommendation and allocation for true MTDC's are useful in assessing performance, it is also beneficial to consider the entire distribution of selected dose combination, as it provides more detailed information as to what combinations are being recommended if a true acceptable MTDC is missed. Cheung [26] proposes to use the accuracy index, after N patients, defined for each row i as

$${\mathcal{A}}_i=1-J\times \frac{\sum _{j=1}^J\mid \pi \left(d_{ij}\right)-\varphi \mid \times {\rho }_{ij}}{\sum _{j=1}^J\mid \pi \left(d_{ij}\right)-\varphi \mid },$$

where π(d_ij) is the true toxicity probability and ρ_ij is the probability of selecting dose combination d_ij as the MTDC in row i. The maximum value of A_i is 1 with larger values (close to 1) indicating that the method possesses high accuracy.

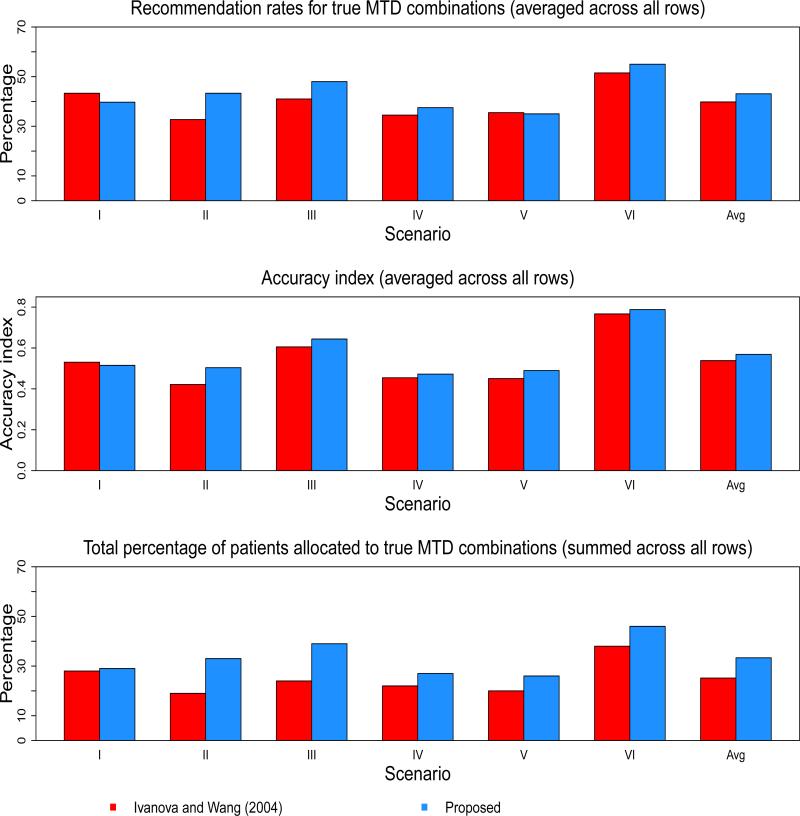
Tables 4 and 5, as well as Figure 2, show the operating characteristics of the two methods under the 6 scenarios. Table 6 reports the proportion of trials that correctly identified 0, 1, 2, and 3 MTDC's. The results contained in Table 6 are not compared to Ivanova and Wang due to the fact that their paper does not report these results. In Scenario 1, the method of Ivanova and Wang yields a higher PCR in two of the three rows and an average PCR of 43.3% across all rows, compared with 39.7% for the proposed approach. These findings are also reflected in the average accuracy index across all rows (0.5304 for Ivanova and Wang vs. 0.5151 for proposed). For patient experimentation, the proposed method allocates a higher percentage of patients to true MTDC's in two of the three rows in Scenario 1, and yields a slightly higher average PCA (29%) than Ivanova and Wang (28%). In Scenario 2, the proposed method outperforms Ivanova and Wang in each row in terms of accuracy index. The methods perform equally in PCR in row 2, while Ivanova and Wang has better performance with regards to PCA in row 2. For the proposed method, the average PCR, PCA, and ${\mathcal{A}}_i$ across all rows of Scenario 2 are 43.3%, 33%, and 0.5036, respectively. These values are 32.7%, 19%, and 0.4213, respectively, for Ivanova and Wang, indicating improved performance with the proposed approach. The relative performance of the methods in Scenario 2 appears to hold for Scenario 3 as well. The proposed method has better PCR and PCA in two of the three rows, and a higher overall average across all rows of the three indices. The most striking difference among the methods seems to be in patient experimentation. In Scenario 3, the average PCA across the rows is 39% for the proposed method, compared to 24% for Ivanova and Wang.

Table 4.

Proportion of recommendation for a combination as the maximum tolerated dose combination within each dose level of agent B. The target toxicity rate is ϕ = 0.20. The total sample size is N = 54 in Scenarios I–III, and N = 36 in Scenarios IV–VI.

		Ivanova and Wang (2004)						Avg ${\mathcal{A}}_n$	Proposed Method						Avg ${\mathcal{A}}_n$
Scenario		1	2	3	4	5	6		1	2	3	4	5	6
I	3	0.30	0.48	0.20	0.02	0.00	0.00	0.530	0.38	0.40	0.20	0.02	0.00	0.00	0.515
	2	0.02	0.29	0.55	0.12	0.01	0.01		0.05	0.32	0.47	0.14	0.02	0.00
	1	0.00	0.08	0.26	0.28	0.27	0.11		0.00	0.05	0.17	0.30	0.32	0.15
II	3	0.03	0.08	0.21	0.32	0.25	0.11	0.421	0.02	0.06	0.17	0.29	0.31	0.15	0.504
	2	0.00	0.01	0.07	0.22	0.36	0.35		0.00	0.01	0.06	0.20	0.36	0.36
	1	0.00	0.01	0.05	0.16	0.41	0.37		0.00	0.00	0.02	0.09	0.26	0.63
III	3	0.55	0.34	0.09	0.01	0.00	0.00	0.605	0.71	0.23	0.05	0.01	0.00	0.00	0.644
	2	0.11	0.37	0.34	0.15	0.02	0.01		0.18	0.35	0.30	0.14	0.02	0.01
	1	0.00	0.05	0.32	0.31	0.24	0.07		0.00	0.04	0.22	0.38	0.27	0.08
IV	2	0.08	0.25	0.39	0.22	0.06	0.00	0.455	0.10	0.27	0.38	0.21	0.05	0.00	0.472
	1	0.01	0.11	0.33	0.30	0.19	0.05		0.01	0.07	0.30	0.37	0.19	0.05
V	2	0.10	0.26	0.40	0.20	0.04	0.00	0.451	0.12	0.30	0.36	0.17	0.03	0.00	0.490
	1	0.01	0.05	0.21	0.28	0.31	0.14		0.00	0.03	0.15	0.30	0.34	0.17
VI	2	0.62	0.30	0.07	0.01	0.00	0.00	0.767	0.69	0.24	0.06	0.00	0.00	0.00	0.789
	1	0.24	0.41	0.26	0.07	0.01	0.00		0.26	0.41	0.26	0.06	0.01	0.00

Table 5.

Proportion of experimentation at each dose combination. The target toxicity rate is ϕ = 0.20. The total sample size is N = 54 in Scenarios I–III, and N = 36 in Scenarios IV–VI.

		Ivanova and Wang (2004)						% > MTDC	Proposed Method						% > MTDC
Scenario		1	2	3	4	5	6		1	2	3	4	5	6
I	3	0.05	0.07	0.04	0.01	0.00	0.00	0.22	0.12	0.09	0.06	0.02	0.01	0.00	0.23
	2	0.05	0.11	0.17	0.11	0.04	0.01		0.04	0.09	0.11	0.05	0.02	0.01
	1	0.07	0.08	0.08	0.06	0.04	0.01		0.03	0.04	0.07	0.09	0.09	0.06
II	3	0.02	0.03	0.04	0.06	0.05	0.05	0.12	0.02	0.03	0.05	0.07	0.07	0.05	0.14
	2	0.02	0.04	0.06	0.10	0.12	0.07		0.02	0.02	0.04	0.07	0.09	0.09
	1	0.06	0.06	0.07	0.07	0.06	0.02		0.02	0.02	0.03	0.05	0.08	0.17
III	3	0.06	0.05	0.03	0.01	0.00	0.00	0.45	0.19	0.06	0.03	0.01	0.00	0.00	0.39
	2	0.08	0.12	0.14	0.11	0.06	0.01		0.07	0.09	0.08	0.05	0.02	0.01
	1	0.06	0.07	0.09	0.06	0.03	0.01		0.03	0.04	0.08	0.11	0.08	0.05
IV	2	0.07	0.11	0.14	0.11	0.06	0.01	0.23	0.09	0.11	0.13	0.08	0.03	0.01	0.27
	1	0.11	0.12	0.13	0.08	0.04	0.01		0.06	0.07	0.13	0.14	0.10	0.05
V	2	0.06	0.09	0.14	0.13	0.07	0.01	0.23	0.09	0.11	0.13	0.08	0.03	0.01	0.21
	1	0.10	0.11	0.12	0.09	0.06	0.02		0.04	0.06	0.09	0.13	0.13	0.09
VI	2	0.22	0.16	0.09	0.02	0.01	0.00	0.42	0.30	0.10	0.04	0.01	0.00	0.00	0.37
	1	0.20	0.16	0.10	0.03	0.01	0.00		0.17	0.16	0.13	0.06	0.02	0.01

Figure 2.

Summary of the operating characteristics of the 2 methods in all scenarios.

Table 6.

Proportion of trials that correctly recommend 0, 1, 2, and 3 maximum tolerated dose combinations.

Scenario	0	1	2	3
I	0.17	0.46	0.32	0.05
II	0.18	0.43	0.29	0.10
III	0.11	0.41	0.40	0.08
IV	0.38	0.52	0.10	-
V	0.41	0.49	0.10	-
VI	0.15	0.62	0.23	-

In Scenarios IV and V, the methods split better performance across each row, with Ivanova and Wang yielding higher PCR in row 2 of each scenario and the proposed method having higher PCR in row 1 of each scenario. An interesting finding in Scenario V relates to ${\mathcal{A}}_i$, in that the proposed method demonstrates a higher average ${\mathcal{A}}_i$ value, even though Ivanova and Wang has a slightly higher average PCR. Recall that the accuracy index accounts for the entire distribution of MTDC recommendation. In this case, the ${\mathcal{A}}_i$ for Ivanova and Wang is penalized in row 2 because it recommends dose d₂₄ with true probability 0.40 more often than the proposed method, while the proposed method recommends d₂₂ with true probability 0.16 more often than Ivanova and Wang. This illustrates the fact that it is important to take into consideration the dose combinations that are being recommended when the true MTDC is not selected. If a method misses the true MTDC, we should hope that it would recommend the dose combination with a true probability next closest to the TTR as the MTDC. Finally, in Scenario 6, the methods perform equally in row 1, with a slight edge given to the proposed method in row 2 for all performance indices. In summary, across all scenarios, Ivanova and Wang and the proposed method yielded average PCR across all rows of 39.8% and 43.1%, respectively. The average ${\mathcal{A}}_i$ across all rows was 0.5381 for Ivanova and Wang, and 0.5687 for the proposed approach. Finally, the largest disparity occurred in overall average PCA, with the proposed method resulting in 33.3% and Ivanova and Wang 25.2%. In assessing safety, the proposed method yielded average DLT rates close to the TTR in each scenario {20.9%, 16.3%, 22.2%, 19.8%, 19.7%, 24.2%}. Also with regards to safety, we compared the proportion of patients treated at combinations above the MTDC for each method. In Scenarios I, II, and IV, the Ivanova and Wang method allocated less patients to overly toxic combinations, while the proposed method did so in Scenarios III, V, and VI.

6. Conclusions

Many of the existing Phase I methods for combination studies are designed to locate a single MTDC from a two-dimensional grid of treatments. In this paper, we have introduced a new method for Phase I combinations studies that identifies a MTDC in each row of a drug combination matrix. This set of recommended MTDC's forms an equivalence contour in two dimensions. We have compared the operating characteristics of the proposed method with existing methodology, and the proposed approach compares favoraby. We recognize that measures such as average PCR and average accuracy index are difficult measures to interpret in this setting, in which recommended combinations are vectors. This has previously been discussed in multiple MTD dose finding in the case of multiple risk groups [27], and currently there is no consensus about how best to assess performance and compare competing methods. In the simulation results, we restricted the possible values for the shift between the MTDC of two adjacent rows to {0, 1, 2, 3}, meaning that the working models do allow for shifts larger than 3 from one row to the next. Results in Supplemental Web Materials investigate the impact of allowing for larger shifts, which equates to including more working models. Specifically, 2 more working models (i.e. shifts of 4 and 5) would be needed in the 2 × 6 case, and 6 more models would be needed in the 3 × 6 case. The results indicate that the performance is very similar to the original results for 2 × 6 grids, and diminishes only slightly for the 3 × 6 grids. These results can be seen in Supplemental Web Material Tables 1 and 2. The method also demonstrated robustness to skeleton choice for three 2 × 6 scenarios (see Supplemental Web Material Tables 6–10). While we have provided a link to access user friendly R code for simulating the operating characteristics of this work, we intend to make functions available for both implementing and simulating the design in an R library. The methods outlined in this manuscript can also be applied to other two-dimensional dose-finding problems, such as those aiming to estimate an MTC under multiple treatment schedules [28, 29].