Fig. 1.

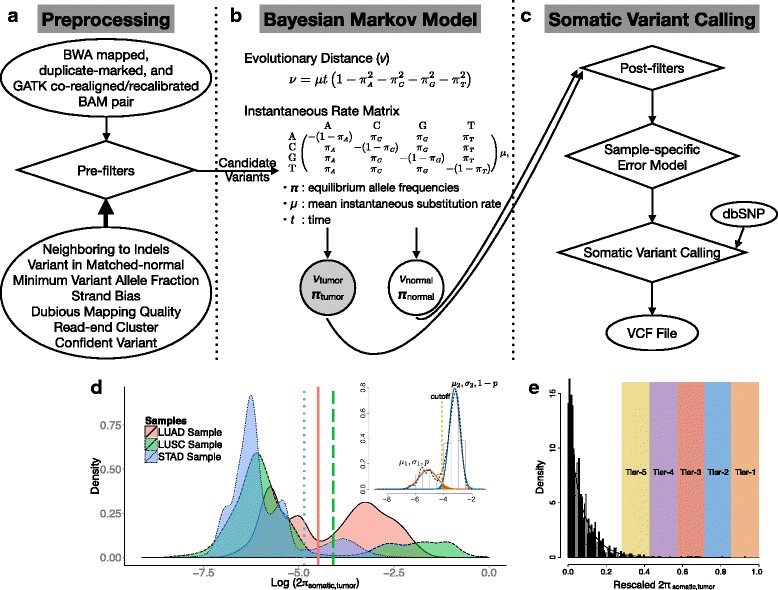
Flowchart of the somatic point mutation caller MuSE. a MuSE takes as input the Burrows-Wheeler Aligner-aligned BAM sequence data from the pair of tumor and normal DNA samples. The BAM sequence data are processed by following the Genome Analysis Toolkit Best Practices. Next, at each genomic locus, MuSE applies seven heuristic pre-filters to screen out false positives resulting from correlated sequencing artifacts. b MuSE employs the F81 Markov substitution model of DNA sequence evolution to describe the evolution from the reference allele to the tumor and the normal allelic composition. It writes to an output file the MAP estimates of four allele equilibrium frequencies (π) and the evolutionary distance (ν). c MuSE uses the MAP estimates of π to compute the tier-based cutoffs by building a sample-specific error model. MuSE deploys two different methods of building the sample-specific error model for the respective WES data and WGS data. Besides using the sample-specific error model, MuSE takes into account the dbSNP information by requiring a more stringent cutoff for a dbSNP position than for a non-dbSNP position. The final output is a Variant Call Format file that lists all the identified somatic variants. d Illustration of the sample-specific error model for WGS data. Tumor heterogeneity is illustrated using TCGA lung adenocarcinoma (LUAD), lung squamous cell carcinoma (LUSC), and stomach adenocarcinoma (STAD) WGS data. All π _somatic selected for building the sample-specific error models are used to draw the densities that are on the logarithmic scale. At the top right, we show a two-component Gaussian mixture distribution with means μ ₁ and μ ₂, standard deviations σ ₁ and σ ₂, and weights p and 1−p, for true negative and true positive, respectively. The expected false positive probability caused by the identified cutoff is the area labeled in red (on the right side of the cutoff), and the false negative probability is the area labeled in blue (on the left side of the cutoff). We first identify a cutoff that minimizes the sum of the two probabilities and add tiered cutoffs that are less stringent than the first one. e Illustration of the sample-specific error model for WES data. Selected π _somatic are rescaled to fit a beta distribution. Tiers 1 to 5 are labeled for illustration purposes, but not in equal proportion to those in the real data