Figure 1. Method summary.

(a) Equivalence between Ecopath and Lotka–Volterra models: simplified diagram of trophic flows between one consumer C and one resource R parameterized with Ecopath model (in blue) and Lotka–Volterra model (in green). B is biomass (t km⁻²), (P/B)_c and (Q/B)_c are the production/biomass and consumption/biomass ratios of C respectively (per year), DC_cr is the proportion of resource R in the diet of consumer C, e_rc expresses the efficiency of a consumer to convert resource energy into biomass with e_rc=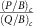. (b) Community matrix construction: derivation of community matrix elements for the simplified food web presented in diagram A, and an example of community matrix structure observed in real food webs. (c) Measure of stability: the eigenvalues of a large community matrix are uniformly distributed on a circle on the complex plane (axes cross at the origin). On the real axis, the dominant eigenvalue Re(λ_max)=R−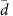, where the centre of the circle 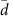is equal to the mean of intraspecific interaction terms 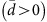, and the radius R is related to interspecific interaction terms (that is, off-diagonal elements of the community matrix) and is equal to 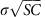in random matrices. For predator-prey communities, the eigenvalues are uniformly distributed on an ellipse with a horizontal half axis 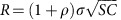(ref. ¹¹).