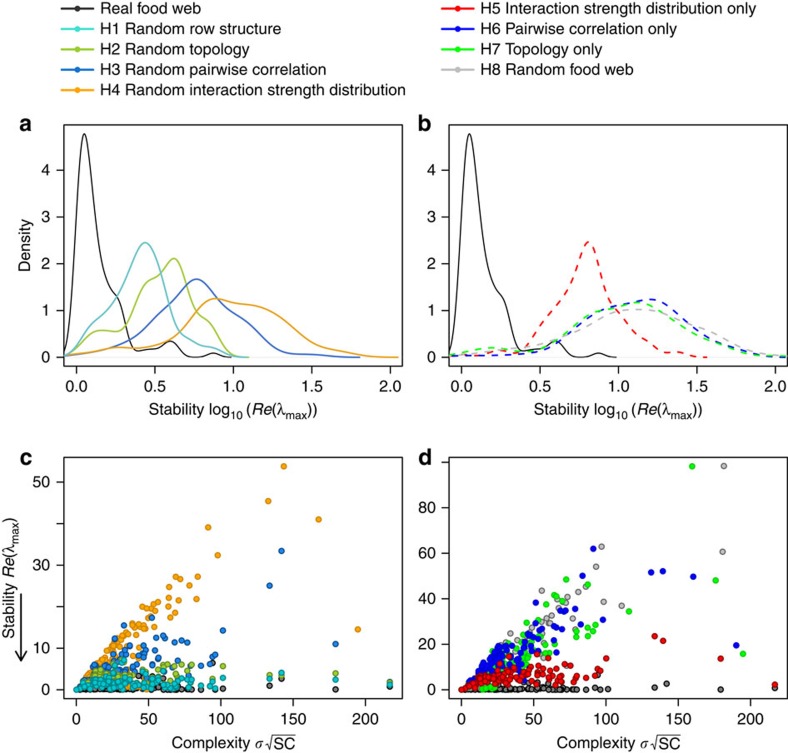
Figure 4. Complexity–stability relationship in empirical and permuted food webs.
Frequency distributions of eigenvalues of real and permuted food webs : (a) permutation tests H1 to H4, (b) permutation tests H5 to H8. Eigenvalues are on a logarithmic scale and dimensionless. Permutation tests were carried out 1,000 times for each food web. Eigenvalue distributions were smoothed using a kernel density estimate of 0.28. (c) Stability of real and permuted food webs related to complexity (permutation tests H1–H4). Stability is measured as Re(λmax) and 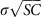 corresponds to complexity. Statistics of the linear regression between complexity and stability: real food webs (slope=0.005, P=0.02, R2=0.04), H1: random row structure (slope=0.003, P=0.38, R2=0.002), H2: random topology (slope=0.006, P=0.2, R2=0.006), H3: random pairwise correlation (slope=0.06, P=10−7, R2=0.2), H4: random interaction strength distribution (slope=0.24, P<10−16, R2=0.65). (d) Stability of permuted food webs related to complexity (permutation tests H5–H8). Statistics of the linear regression between complexity and stability: H5: empirical distribution of interaction strengths only (slope=0.06, P=10−9, R2=0.25). H6: pairwise correlation only (slope=0.3, P<10−16, R2=0.63). H7: topology only (slope=0.32, P<10−16, R2=0.6). H8: random food webs (slope=0.33, P<10−16, R2=0.66).
corresponds to complexity. Statistics of the linear regression between complexity and stability: real food webs (slope=0.005, P=0.02, R2=0.04), H1: random row structure (slope=0.003, P=0.38, R2=0.002), H2: random topology (slope=0.006, P=0.2, R2=0.006), H3: random pairwise correlation (slope=0.06, P=10−7, R2=0.2), H4: random interaction strength distribution (slope=0.24, P<10−16, R2=0.65). (d) Stability of permuted food webs related to complexity (permutation tests H5–H8). Statistics of the linear regression between complexity and stability: H5: empirical distribution of interaction strengths only (slope=0.06, P=10−9, R2=0.25). H6: pairwise correlation only (slope=0.3, P<10−16, R2=0.63). H7: topology only (slope=0.32, P<10−16, R2=0.6). H8: random food webs (slope=0.33, P<10−16, R2=0.66).