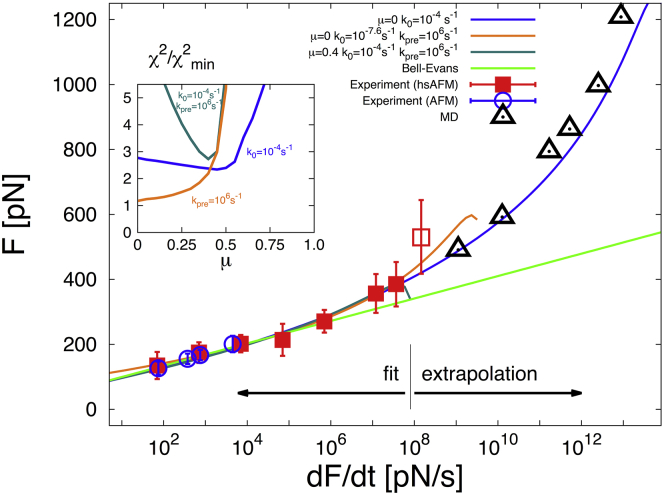
Figure 4.
Titin unfolding. Mean rupture force of the titin I91 domain, when pulled from its two termini, as a function of the logarithm of the force loading rate from hsAFM (red squares) (20) and regular AFM experiments (blue circles) (19), and from MD simulations (black triangles) (21). Error bars indicate SDs. The analytic expression for in Eq. 5 was fitted only to hsAFM data (solid squares) (19). The point at the highest loading rate (open square) was not included in the fit because it proved difficult to estimate all the relevant correction factors (in particular the very large viscous drag correction, and the linker correction (see Cossio et al. (23) and the Supporting Material) required to determine the effective force loading rate). However, if these estimates are correct and the data value is proper, the overlap of experiment and MD would be poor. Least-square fits are shown for μ → 0 with fixed close to the bulk unfolding rate (blue line), and fixed kinetic prefactor (orange), and for μ = 0.4 with both and fixed (dark green). (Inset) The error relative to the best fit as a function of brittleness μ. A fit of the perfectly brittle Bell-Evans model (3, 6) for is shown as a light-green line. For the best fits , the distance to the transition state and the activation barrier are in the ranges and , respectively. To see this figure in color, go online.