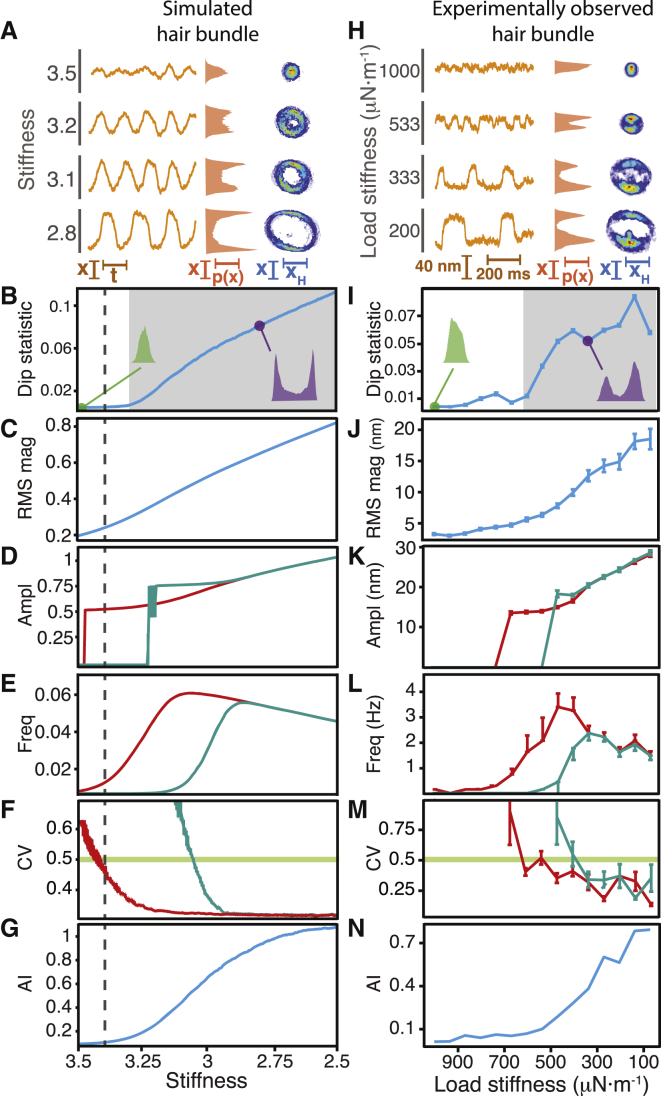
Figure 3.

Traversing a supercritical Hopf bifurcation by altering the load stiffness. (A–N) Over a range of load stiffnesses, we compared the behavior of a model hair bundle crossing a supercritical Hopf bifurcation (A–G) with that of an experimentally observed hair bundle (H–N). All of the panels depicted here display the same metrics as shown in Fig. 2. (A and H) As the stiffness declined, the amplitude of spontaneous oscillation rose (left), the position histogram became bimodal (middle), and the diameter of the limit cycle increased (right). (B and I) The dip statistic rose as the stiffness decreased, signaling the emergence of bimodal position histograms and the onset of spontaneous oscillations (shaded; p < 10⁻³). The estimated boundary of the oscillatory regime occurred on the oscillatory side of the deterministic bifurcation (dashed line). (C and J) The RMS magnitude rose gradually as the stiffness decreased. (D and K) The amplitude increased with a decrease in stiffness. For these and subsequent panels, we used peak-detection thresholds of (D–F) 1 (red) and 1.5 (cyan) or (K–M) 26 nm (red) and 34 nm (cyan). (E and L) The stiffness at which the frequency rose depended on the value of the peak-detection threshold. Spontaneous oscillations emerged with a frequency that first rose and subsequently fell with decreases in stiffness. (F and M) The stiffness at which the coefficient of variation exceeded 0.5 depended on the threshold value. (G and N) The analytic information rose gradually as the stiffness decreased. For all panels, the constant force was zero with a gain of 0.1. The stiffness and drag coefficient of the stimulus fiber were 109 μN⋅m⁻¹ and 142 nN⋅s⋅m⁻¹, respectively. Dashed lines correspond to the location of the supercritical Hopf bifurcation in the absence of noise. Stochastic simulations employed noise with standard deviations of σ_x = σ_f = 0.1. The error bars represent the standard errors of the means.