A non-negative matrix factorization method for detecting modules in heterogeneous omics multi-modal data

Abstract

Motivation: Recent advances in high-throughput omics technologies have enabled biomedical researchers to collect large-scale genomic data. As a consequence, there has been growing interest in developing methods to integrate such data to obtain deeper insights regarding the underlying biological system. A key challenge for integrative studies is the heterogeneity present in the different omics data sources, which makes it difficult to discern the coordinated signal of interest from source-specific noise or extraneous effects.

Results: We introduce a novel method of multi-modal data analysis that is designed for heterogeneous data based on non-negative matrix factorization. We provide an algorithm for jointly decomposing the data matrices involved that also includes a sparsity option for high-dimensional settings. The performance of the proposed method is evaluated on synthetic data and on real DNA methylation, gene expression and miRNA expression data from ovarian cancer samples obtained from The Cancer Genome Atlas. The results show the presence of common modules across patient samples linked to cancer-related pathways, as well as previously established ovarian cancer subtypes.

Availability and implementation: The source code repository is publicly available at https://github.com/yangzi4/iNMF.

Contact: gmichail@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Technological advances allow biomedical researchers to collect a wide variety of omics data on a common set of samples. Data repositories such as The Cancer Genome Atlas (TCGA) provide multiple types of omics data, thus enabling in-depth investigation of molecular events at different stages of biology and for different tumor types. However, the latter task requires developing methods for data integration, a topic that has received increased attention in the literature.

In genomic studies, the integration of multifaceted data is becoming increasingly viable and insightful (Gehlenborg et al., 2010; Imielinski et al., 2012; Jörnsten et al., 2011; Mo et al., 2013). Cellular signals and processes depend on the coordinated interaction and communication among a wide variety of biomolecules including genes, proteins, metabolites and epigenetic regulators. There are multiple layers in which regulation takes place and therefore multiple vantage points from which to observe biological activity. A joint analysis of data on the same set of samples from multiple omics sources has potential to achieve more perceptive results over separate analyses, as well as provide a more comprehensive global view of the biological system.

A key challenge for integration methods is dealing with heterogeneous data. Data from different sources are difficult to compare due to inherent discrepancies. Different genomic variables are measured and collected in different ways, and they are associated with different types of noise and confounding effects. Most importantly, they represent different aspects of the biological system. The discrepancy among data sources contributes to a useful multifaceted view of the system, but it also brings forth a new level of complexity that makes it hard to distinguish the coordinated signal.

There are many integration techniques that deal with the complexity of multiple sources by relying on prior knowledge of the relationships that connect them. Some procedures seek to map different experimental data types, such as gene expression (GE), miRNA expression (ME) and copy number variation to a common space of known biological pathways or sets (Khatri et al., 2012; Mitrea et al., 2013 and references therein). Others select features or assign weights to features based on prior knowledge, possibly using such information in a linear-based model (Jauhiainen et al., 2012; Jensen et al., 2007; Stingo et al., 2011) or in a framework for identifying modules (Li et al., 2012; Srihari and Ragan, 2013). All these approaches require the consultation of an external resource, such as signaling pathways or gene interaction networks. While this supervised approach is convenient (and sensible in certain respects), it relies heavily on the external information being valid and representative, which is not always guaranteed, even in the modern era of data availability. In addition, relating variables based on previously established findings can introduce an element of bias and subjectivity that hinders the discovery of new associations.

In contrast to such supervised approaches, our objective is to develop an integration method that directly leverages the advantage of multiple data sources to deal with heterogeneity. In multiple datasets, the signal of interest is typically common among all sources (homogeneous), while extraneous effects tend to differ across sources (heterogeneous). The main principle of our approach is to separate the homogeneous and heterogeneous effects among the sources to extract the coordinated signal from extraneous noise. Many existing integration techniques similarly make the distinction between common and distinct effects across sources, such as those extending the Dirichlet mixture model (Lock and Dunson, 2013) and principal component analysis (PCA, Lock et al., 2013).

Our proposed method extends an integrative non-negative matrix factorization (NMF) framework (Zhang et al., 2012) via a partitioned factorization structure that captures homogeneous and heterogeneous effects. A novel tuning selection procedure allows the model to adapt to the level of heterogeneity among the datasets. We apply our approach to an integrated study of ovarian cancer involving three types of genomic variables and discover multi-dimensional modules exhibiting topological patterns of expression across known cancer-related pathways.

2 Methods

2.1 NMF

NMF is a powerful tool for data reduction and exploration that has seen popular use in analyzing high-throughput genomic data (Brunet et al., 2004; Devarajan, 2008; Tamayo et al., 2007). The method is related to PCA, except that it employs the constraint of non-negativity in lieu of orthogonality. As a result, NMF solutions are less uniquely defined but are more interpretable.

Given non-negative data matrix X_N×M, NMF finds a non-negative factorization WH of rank D that best approximates X, typically in terms of the Frobenius norm (Lee and Seung, 1999):

$$\begin{array}{l}{\min }_{W,H}||X-WH|{|}_F^2\\ \text{s}.\text{t}.W\ge 0,H\ge 0.\end{array}$$

While Euclidean distance assumes a Gaussian distribution of values, alternative formulations of NMF using Bregman divergences have been proposed (Sra and Dhillon, 2005). Bregman divergences, which bear a strong connection with exponential families (Banerjee et al., 2005), emcompass a wide range of distributional assumptions (e.g. Poisson, Exponential and probabilistic distributions). Although we use Euclidean distance in the formulation of our method later, alternative loss functions may be accommodated via adjustments to the algorithm.

The factor $H_{D\times M}$ contains the basic components of the data, while the elements of $W_{N\times D}$ can be thought of as latent factors associated with these components. Thus, each observation (row of X) is approximated by a linear combination of components (rows of H) with weights given by each row of W. The full data are explained by a sum of additive parts. In biological contexts, this is intuitive because biological entities and mechanisms can be naturally described with a signal that is either present or absent.

Because of the constraint of non-negativity of the approximation elements, solutions to NMF are only unique up to scalings and rotations. Specifically, scaling and rotating the columns of W and rows of H appropriately will not alter the overall matrix product WH. For this reason, what is of interest in practice is not the values of the matrix elements, but their relative magnitudes in each column of W or row of H.

At its core, NMF views the data from a different vantage point (the origin) than orthogonality-based approaches (center of mass) such as PCA, partial least squares regression and canonical correlation analysis. Besides being more intuitive, this also offers certain advantages such as the ability to capture context-dependent patterns (Devarajan, 2008). Meanwhile, for our purposes, the flexibility of the factorization is also convenient for dealing with heterogeneous data.

2.2 Joint NMF

Joint NMF (jNMF) was developed as an extension to NMF for integrating multiple datasets with a common set of observations (Zhang et al., 2012). For K data matrices ${(X_1)}_{N\times M_1},\dots ,{(X_K)}_{N\times M_K}$, the formal problem is:

$$\begin{array}{l}{\displaystyle \underset{W,H_1,\dots ,H_K}{\min }}{\displaystyle \sum _{k=1}^K||}{X}_k-W{H}_k|{|}_F^2\\ \text{s}.\text{t}.\hspace{0.17em}W\ge 0,H_k\ge 0,k=1,\dots ,K,\end{array}$$

with $W_{N\times D},{(H_k)}_{D\times M_k}$ producing K rank D approximations. The method can be described as multiple NMF problems subject to a shared factor matrix. Other decomposition-based integration methods have been proposed, including multiple canonical correlation analysis (Witten et al., 2009), multi-block partial least squares (Li et al., 2012) and Joint and Individual Variation Explained (Lock et al., 2013). Such approaches use the orthogonality constraint, whereas jNMF and our proposed method employ non-negativity.

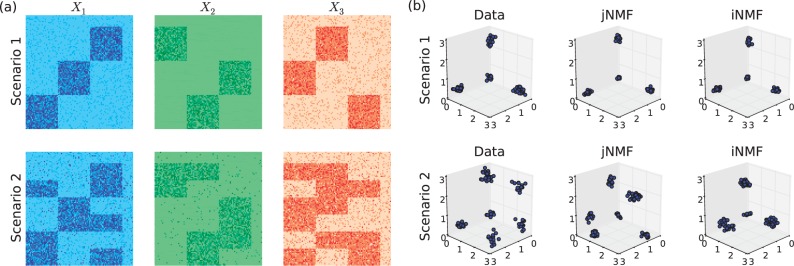
The method was shown to be able to detect coordinated activity across multiple genomic variables in the form of multi-dimensional modules. The exact definition of modules slightly differs across studies (Jin and Lee, 2015; Li et al., 2012; Roy et al., 2013), but their general purpose is to group variables based on common function or association. This serves as a useful preliminary step to reduce the dimensionality of the problem. Multi-dimensional modules capture common signals across multiple sources of data (Fig. 1a). In jNMF, as well as in our method, each module represents a biclustering of both observations and variables, which can be visualized as a block in the data matrix after appropriate rotation.

Fig. 1.

(a) An example of multi-dimensional modules across three different data sources. Three modules are distinguishable in Scenario 1 as strong associations between subsets of variables across sources and a common subset of observations. Scenario 2 contains the same data with added random noise and confounding effects. (b) Low-dimensional representations of the data (X₂), jNMF approximations (W) and iNMF approximations (W). The modules are clearly detected by both methods in Scenario 1 but only by iNMF in Scenario 2 (Color version of this figure is available at Bioinformatics online.)

A limitation of jNMF is that it is not methodologically different from standard NMF. In fact, it is easy to show that the problems are equivalent by setting $\tilde{X}=(X_1,\dots ,X_K)$ and $\tilde{H}=(H_1,\dots ,H_K)$. As a consequence, the optimization step of jNMF does not distinguish between different variable sources when integrating, which is problematic for heterogeneous data.

The toy example in Figure 1 illustrates this. The heatmaps (Fig. 1a) depict two scenarios of a three-source integration problem. In Scenario 1, three modules are easily distinguishable in all sources as blocks, which associate different subsets of variables with the common observation groups. Scenario 2 contains the same data, except with added noise (generated as discussed in Section 3.1). In particular, the additional block structures that are misaligned with the underlying modules represent confounding effects that vary from source to source.

Figure 1b plots (in low-dimensional space) the data and the corresponding solutions of jNMF and our proposed method (iNMF). Both methods clearly distinguish the signal when the signal is clean (Scenario 1), but jNMF is less robust to heterogeneous noise across the sources (Scenario 2). While jNMF is very effective for detecting homogeneous effects, its factorization structure WH_k leaves no room for heterogeneous approximations. As a result, jNMF is sensitive to random noise and confounding effects, because they typically differ in structure across sources. We seek to remedy this via expanding the factorization structure.

2.3 Integrative NMF

Our proposed method, integrative NMF (iNMF), leverages the advantage of multiple data sources to gain robustness to heterogeneous perturbations. While jNMF considers homogeneous effects WH_k, iNMF additionally considers heterogeneous effects $V_k{H}_k$. Formally, for non-negative observationally-linked datasets $X_1,\dots ,X_K$ as defined previously, the optimization problem is the following:

$$\begin{array}{l}{\displaystyle \underset{V_1,\dots ,V_K}{\underset{W,H_1,\dots ,H_K,}{\min }}}{\displaystyle \sum _{k=1}^K||}{X}_k-(W+V_k)H_k|{|}_F^2+\lambda {\displaystyle \sum _{k=1}^K||}{V}_k{H}_k|{|}_F^2\\ \text{s}.\text{t}.\hspace{0.17em}W\ge 0,H_k\ge 0,V_k\ge 0,k=1,\dots ,K.\end{array}$$

To retain identifiability, we penalize the Frobenius norm of the heterogeneous effects $V_k{H}_k$, as WH_k can always be expressed in terms of $V_k{H}_k$ but not vice-versa. Rewriting $V_k{H}_k=(W+V_k)H_k-W{H}_k$, we see that the objective function is simply a partitioned version of the jNMF objective, which penalizes $X_k-W{H}_k$.

The idea of combining homogeneous and heterogeneous parts across sources is reminiscent of the one-way analysis of variance model, in which the total variation is explained by joint and individual effects across groups: $y_i=\mu +{\alpha }_j+{ϵ}_{ij}$. However, while the analysis of variance common effect μ is estimated to be the sample mean, the iNMF homogeneous effect W is actually the element-wise minimum of the approximated latent factors $W+V_k$, since $V_k\ge 0$. For this reason, $W,V_k$ cannot be directly used to infer the level of joint and individual effects among the sources, since W will be overestimated (and V_k underestimated) when parts of the individual effects are homogeneous. Thus, it is more appropriate to refer to $W,V_k$ as approximations of the true joint and individual effects rather than their estimates.

Interestingly, restricting $W\ge 0,V_k\ge 0$ is methodologically equivalent to restricting $W+V_k\ge 0,V_k\le 0$. In the latter, the approximated common factor W represents the element-wise maximum of $W+V_k$, rather than the element-wise minimum. Therefore, imposing non-negativity on V_k does not lead to bias issues but instead a particular perspective on the joint effects. It is also possible to allow for both positive and negative values for V_k if we set $W=\text{mean}(V_k)$, for instance.

The parameter λ can be viewed as the homogeneity parameter, since larger values induce smaller $V_k{H}_k$. When datasets from multiple sources contain homogeneous elements, performing separate analyses (λ = 0) sacrifices power; when datasets contain heterogeneous elements, a purely joint analysis ($\lambda =+\infty$) is sensitive to extraneous noise. Real data consists of a mixture of homogeneous and heterogeneous elements, and likewise iNMF functions as a mixture of jNMF and NMF.

2.4 Algorithm

The classical algorithm for NMF was introduced by Lee and Seung (2001) and consists of simple multiplicative updates derived from auxiliary functions. Over the years, new approaches based on gradient descent and alternating least squares have been proposed (Berry et al., 2007; Lin, 2007), which offer faster convergence and better convergence guarantees. However, these alternatives generally involve an explicit projection step to ensure non-negativity of solutions, whereas with multiplicative updates non-negativity is implicitly guaranteed. We base our algorithm for iNMF on the original method of Lee and Seung (2001), as it provides a more natural and flexible foundation from which to develop extensions.

Beginning with random positive initializations, we perform the following element-wise updates at each iteration until convergence:

$$\begin{array}{l}{W}_{ij}\leftarrow W_{ij}\frac{{({\displaystyle \sum _k{X}_k}{H}_k^T)}_{ij}}{{({\displaystyle \sum _k(W+V_k)}{H}_k{H}_k^T)}_{ij}}\\ {(H_k)}_{ij}\leftarrow {(H_k)}_{ij}\frac{{({(W+V_k)}^T{X}_k)}_{ij}}{{({(W+V_k)}^T(W+V_k)H_k+\lambda V_k^T{V}_k{H}_k)}_{ij}}\\ {(V_k)}_{ij}\leftarrow {(V_k)}_{ij}\frac{{(X_k{H}_k^T)}_{ij}}{{((W+V_k)H_k{H}_k^T+\lambda V_k{H}_k{H}_k^T)}_{ij}}.\end{array}$$

Since the iNMF objective function is non-convex, one should perform many repetitions and choose the minimizer of the objective function as the final solution. The proof of monotonicity of the objective function under these updates is provided in Supplementary Section S1.

2.5 Sparse formulation

Although NMF naturally gives rise to parsimonious solutions (Lee and Seung, 1999), sparsity can be further induced via penalization. We adopt a method similar to the one used in Mankad and Michailidis (2013), which applies the L1-norm to elements of H_k. This produces a slightly different objective function:

$${\displaystyle \sum _{k=1}^K||}{X}_k-(W+V_k)H_k|{|}_F^2+\lambda {\displaystyle \sum _{k=1}^K||}{V}_k{H}_k|{|}_F^2+{\lambda }_s{\displaystyle \sum _{k=1}^K||}{H}_k|{|}_1,$$

and algorithm:

$$\begin{array}{l}{W}_{ij}\leftarrow W_{ij}\frac{{({\displaystyle \sum _k{X}_k}{H}_k^T)}_{ij}}{{({\displaystyle \sum _k(W+V_k)}{H}_k{H}_k^T)}_{ij}}\\ {(H_k)}_{ij}\leftarrow {(H_k)}_{ij}\frac{{({(W+V_k)}^T{X}_k)}_{ij}}{{({(W+V_k)}^T(W+V_k)H_k+\lambda V_k^T{V}_k{H}_k)}_{ij}+{\lambda }_s}\\ {(V_k)}_{ij}\leftarrow {(V_k)}_{ij}\frac{{(X_k{H}_k^T)}_{ij}}{{((W+V_k)H_k{H}_k^T+\lambda V_k{H}_k{H}_k^T)}_{ij}}.\end{array}$$

A similar sparsity formulation involving the same penalization term can be derived for jNMF.

2.6 Tuning selection

As with other sparse NMF formulations (Gao and Church, 2005; Kim and Park, 2007; Mankad and Michailidis, 2013), the sparsity parameter λ_s is best left to be chosen manually to adjust for interpretability, although too large of a choice leads to degenerate solutions. For selecting the number of modules D, a common method is to use a consensus-based approach (Brunet et al., 2004), which determines the credibility of each tuning choice based on the stability of the corresponding solutions. From basic intuition, given the most appropriate ranks $D_k,k=1,\dots ,K$ for individual datasets, the integrated rank should lie somewhere between ${\max }_k{D}_k$ and ${\sum }_k{D}_k$. However, it is sometimes preferable to choose a smaller rank for a simpler representation consisting of the top D modules.

Although a consensus-based strategy may be used for the homogeneity parameter λ, the nature of the iNMF framework allows a simpler procedure. To separate the homogeneous and heterogeneous parts, we rely on measuring the level of heterogeneity across the sources. We do this by comparing the objective values of jNMF, which represent complete homogeneity, and separate NMFs (sNMF), which represent complete heterogeneity.

Given a decreasing sequence of λ, the procedure is as follows:

• 1. Perform jNMF and sNMF on the datasets and store the unsquared residual quantities:

  $$R_J={\displaystyle \sum _k||}{X}_k-W^{(J)}{H}_k^{(J)}|{|}_F,R_S={\displaystyle \sum _k||}{X}_k-W_k^{(S)}{H}_k^{(S)}|{|}_F.$$
• 2. For each λ in the decreasing sequence:

  • a. Perform iNMF with homogeneity parameter λ and store:

    $$R_I^{(\lambda )}={\displaystyle \sum _k||}{X}_k-W^{(I,\lambda )}{H}_k^{(I,\lambda )}|{|}_F.$$
  • b. If $R_I^{(\lambda )}-R_J>2(R_J-R_S)$, then stop and select the previous λ.

By selecting the smallest λ for which the threshold is not exceeded, we seek to attribute as much of the data as possible to heterogeneous effects ($V_k{H}_k$) before overfitting. Here, overfitting is detected when the difference between the iNMF and jNMF residuals, $R_I^{(\lambda )}-R_J$, becomes significantly large, as typically we would expect jNMF to detect some of the joint signal. More discussion on this procedure can be found in Supplementary Section S2.

3 Results

3.1 Simulation study

We compare jNMF and iNMF based on their abilities to identify the structure of the true modules, which amounts to identifying the correct biclusters of observations and variables. We generated data based on a joint block diagonal structure representing the modules (or joint effects) of interest. We then perturbed the data using three different methods, as follows. To simulate heterogeneous effects from extraneous factors, we randomly add blocks with probability σ_h to the base structures. These blocks are aligned with the columns of the modules but not their rows so as to be heterogeneous with respect to variable sources. To simulate random noise, we applied two types of error (scattered and uniform) independently to each data cell. Scattered error switches each entry value between zero and nonzero with probability σ_s, while uniform error adds a random $\text{Unif}(-{\sigma }_u,{\sigma }_u)$ variable to the entry and takes the absolute magnitude. Further details on the data generation process can be found in Supplementary Section S3. The final generated data matrices resemble those in the bottom row of Figure 1a.

The Frobenius norm error of the approximation is not useful here as a performance measure, since the goal is to identify the true modules rather than to approximate the data. Instead, we measure the level of signal detected relative to noise by considering the matrices WH_k, which represent the approximated homogeneous effects. For each dataset X_k, the module detection score S is defined as:

$$S={({\mu }_{\text{signal}}-{\mu }_{\text{noise}})}_{+}/{\mu }_{\text{signal}},$$

where ${\mu }_{\text{signal}},{\mu }_{\text{noise}}$ are the averages of the values of WH_k that lie inside and outside of the true modules, respectively. This score is invariant to rotations and scalings of $W,H_k$, and it measures how well observations and variables are grouped according to the true modules. We take the average score S over all K data sources as the final module detection score.

We compared the performance of jNMF and iNMF (200 repetitions used in each) under four different data scenarios: baseline (i), large number of modules (ii), large size of modules (iii) and large number of datasets (iv). Figure 2 plots the average ratios between the iNMF and jNMF detection scores. Under high levels of scattered and heterogeneous error, iNMF significantly outperforms jNMF in identifying the true modules. Higher levels of uniform error do not seem to lead to significant differences. The two methods are only comparable under homogeneous and noise-free settings. This adaptivity of iNMF allows for robustness to heterogeneous noise.

Fig. 2.

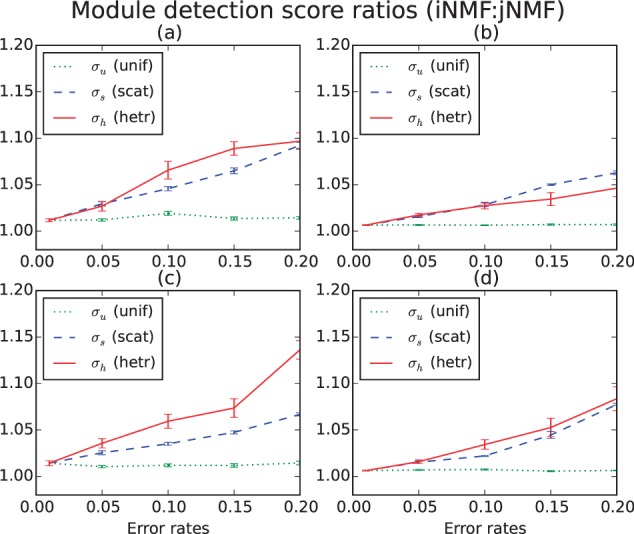
Average ratios (iNMF:jNMF) of detection performance (S) over 25 trials (with standard errors) under four data and module dimensions, with three types of perturbations (uniform, scattered, heterogeneous). The leftmost common point in each subplot represents the error scenario ${\sigma }_u={\sigma }_s={\sigma }_h=0.01$, while each trajectory represents raising the level of a single type of error. (a) Two sources of 40 × 40, four modules of 8 × 8; (b) two sources of 80 × 80, eight modules of 8 × 8; (c) two sources of 72 × 72, four modules of 16 × 16 and (d) four sources of 40 × 40, four modules of 8 × 8 (Color version of this figure is available at Bioinformatics online.)

3.2 Data preparation and preprocessing

We conduct a joint analysis of genetic and epigenetic variables to study biomarkers associated with ovarian cancer. The data were downloaded from TCGA on August 28, 2014, from the platforms Illumina 27K [DNA methylation (DM)], Agilent G4502A-07-2, Agilent G4502A-07-3 (GE) and Agilent H-miRNA 8x15K v2 (ME). All variables were Level 3 processed. The full data consist of 15 661 DM, 14 821 GE and 799 ME variables from a common set of 592 ovarian cancer samples.

Variables with missing observations were omitted. Variance stabilization and non-negativity transformations were applied as follows. GE data were randomly truncated at $-4+\text{ϵ}$ and $4-\text{ϵ}$ where $\text{ϵ}\sim \text{i}.\text{i}.\text{d}.\hspace{0.17em}\text{Unif}(0,{10}^{-3})$ and then shifted +4 units. This is equivalent to applying the function $f(x)=\min \left\{\max \right\{x,-4+\text{ϵ}\},4-\text{ϵ}\}+4$ to each entry. Random truncations serve to prevent data singularity issues. ME data were log 2 transformed, truncated at $2+\text{ϵ}$ and $6-\text{ϵ}$ with the same method and shifted −2 units. Each dataset (DM, GE and ME) was then normalized according to its within-source standard deviation. Other normalization strategies are discussed in Supplementary Section S4. Next, we removed DM variables with means below the 15th percentile, and then DM and GE variables with variances below the 15th percentile, which produced the final datasets described above. This filtering procedure is similar to the one used in Zhang et al. (2011).

3.3 Module discovery and validation

We performed the sparse versions of jNMF and iNMF (200 repetitions each) on the post-processed TCGA data with $\lambda =0.1$ (as chosen by our selection procedure) for a range of sparsity parameter choices ${\lambda }_s={10}^{-4},{10}^{-3},0.01,0.1,1$. We first evaluated the validity of the findings based on concordance with reference DM, GE and ME variables clusters from relevant literature. These reference clusters consist of either two or four groups of variables each, and so we chose D = 2, 4 to allow for appropriate comparisons. Our own empirical variable clusters were computed from the factor matrices H_k. We normalized each row of H_k by its mean and assigned each variable to a cluster $1,\dots ,D$ based on the maximum in each column.

Our first two reference clusters were derived from an integrative study of ovarian cancer by Bell et al. (2011) using DM, GE, ME and DNA copy number variation data from TCGA. Consensus NMF (csNMF) clustering established four disease subtypes based on prominent gene markers in each cluster. These four groups of genes, and their associated DM variables (information provided by TCGA), comprised our reference GE and DM clusters. Another integrated analysis by Creighton et al. (2012) identified sets of miRNAs significantly associated with better or worse survival rates for ovarian cancer patients. We used these two groups of variables as our ME reference. A full list of these reference clusters is provided in Supplementary Section S5.

We assessed concordance between our empirical results and the reference using two metrics, the Gini impurity index (Hastie et al., 2009) and the cluster purity Kim and Park (2008). The Gini index for empirical cluster i is defined as:

$$I_i={\displaystyle \sum _{d=1}^D{\widehat{p}}_{d,i}}(1-{\widehat{p}}_{d,i}),$$

where ${\widehat{p}}_{d,i}$ is the proportion of elements in empirical cluster i belonging to reference cluster d. For each data source, we compute this quantity for each empirical cluster $i=1,\dots ,D$ and take the average as the impurity score I. The cluster purity is defined as:

$$P=\frac{1}{n}{\displaystyle \sum _{i=1}^D\underset{1\le d\le D}{\max }\hspace{0.17em}}n(d,i),$$

where n is the total number of members in all empirical clusters and n(d, i) is the number of members of empirical cluster i belonging to reference cluster d. I measures the level of disagreement within each empirical cluster, and P measures the level of agreement between the empirical and reference clusters.

For each of these statistics, we simulated null distributions (1000 samples) by randomizing cluster assignments. Table 1 compares the impurity and purity scores with respect to all three reference clusters, applied to modules obtained by jNMF and iNMF (as well as from the null distribution) for a range of sparsity parameter choices. We see that the iNMF clusters are generally more concordant with established findings as well as more stable, as evidenced by the scores corresponding to the GE reference. This reflects iNMFs ability to more clearly distinguish the joint signals in the midst of heterogeneous confounders that are likely present among the DM, GE and ME variables.

Table 1.

Impurity (I) and purity (P) scores (in percentages) of empirical clusters obtained from jNMF and iNMF with respect to three reference clusters

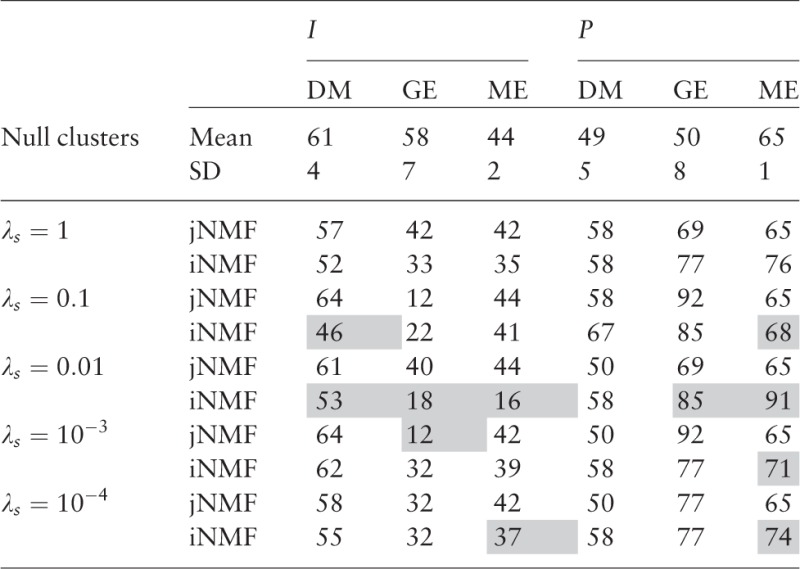Shading indicates significantly ($\ge 2$ SD) higher concordance compared with both the alternative method and the null distribution.

The second step of our validation involves assessing the observational clusters generated by our modules (using the results for $\lambda =0.1,D=4$). Similar to before, we partitioned our 592 observations into four groups based on the maximum value within each row of the column-mean normalized W matrix. We compared these clusters with results from Bell et al. (2011) [results obtained from Verhaak et al. (2013)] and Hofree et al. (2013) who analyzed samples overlapping with ours. The first group used csNMF clustering, while the second applied a network-regularized NMF (netNMF) based on networks from public databases. Concordance tables are presented in Table 2.

Table 2.

Overlap in membership between observational clusters

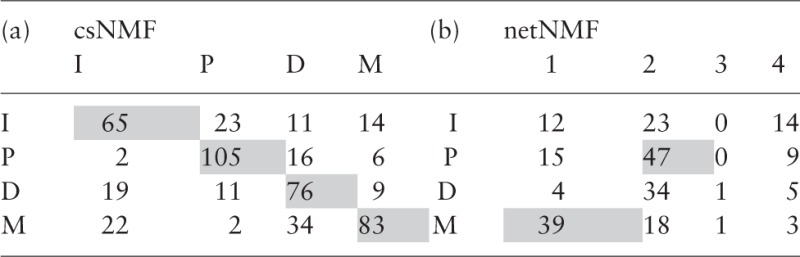Our results from iNMF are concordant with (a) csNMF clusters (498 samples) but not with (b) netNMF clusters (225 samples). Shading indicates maxima in both rows and columns.

Our empirical clusters largely coincide with those of csNMF, indicating that the underlying true signal among DM, GE and ME variables is strong. However, there are some discrepancies, particularly among the modules (I) and (M). This suggests that the samples from these modules contain higher levels of heterogeneous noise. Because iNMF is able to adjust to this type of noise, its clusters are likely a more accurate reflection of the true clusters. Meanwhile, there is not as strong concordance between iNMF and netNMF clusters, which is likely due to the influence of external network information in the latter method. While the incorporation of such information brings in new perspectives, the reliability of the procedure is heavily dependent on the accuracy and relevance of the information. In addition, tuning selection is a delicate issue, as it is difficult to determine where exactly the underlying truth lies between what are suggested by observed patterns and prior input.

Although relying on external information can be useful in guiding the analysis, there are a few disadvantages. One is that such information may be unreliable. Although public databases are becoming increasingly extensive and well-curated, their results are nevertheless aggregated from many studies with different designs and objectives and are thus prone to accumulated errors and oversimplification. Incorporating additional information can be misleading if the information is messy or incongruous with the research question, as demonstrated in our validation step with observational clusters.

Furthermore, when the procedure is supervised, findings will naturally tend toward the reference. This is somewhat favorable, since results that largely deviate from well-established findings are less credible. However, for the purpose of discovery, there is limited utility in selecting new candidates based solely on existing results. It is less subjective to withhold external information until after the analysis. We address both of these concerns by performing integration independently of enrichment, thereby allowing our module discovery step to be data-driven rather than input-driven.

3.4 Follow-up module analysis

Current methods of attaching biological relevance to discovered modules frequently involve enrichment according to either pathways gathered from various gene or interaction databases or experimental results (Jin and Lee, 2015; Li et al., 2012; Roy et al., 2013; Zhang et al., 2012). In such studies, the number of modules being considered is very high, which is suitable for associating with large collections of biological pathways and interactions. In contrast, our study deals with substantially fewer modules, which represent broader effects that are more appropriately associated with disease subtypes. Our analysis will span multiple cancer-related pathways extracted from BioCarta and relevant literature. Based on the distribution of module expression among these pathways, we will observe topological patterns of genomic expression and connect them with ovarian cancer subtypes.

For the rest of this section, we will focus on the modules discovered by iNMF at ${\lambda }_s=0.01$, as they appear to be most concordant with the reference variable clusters, in particular the GE cluster that is associated with four subtypes of ovarian cancer: immunoreactive, proliferative, differentiated and mesenchymal (Bell et al., 2011). These subtypes were defined based on high expression of gene markers associated with responsiveness to antigens (I), proliferation (P), cell differentiation (D) and stromal cell development (M).

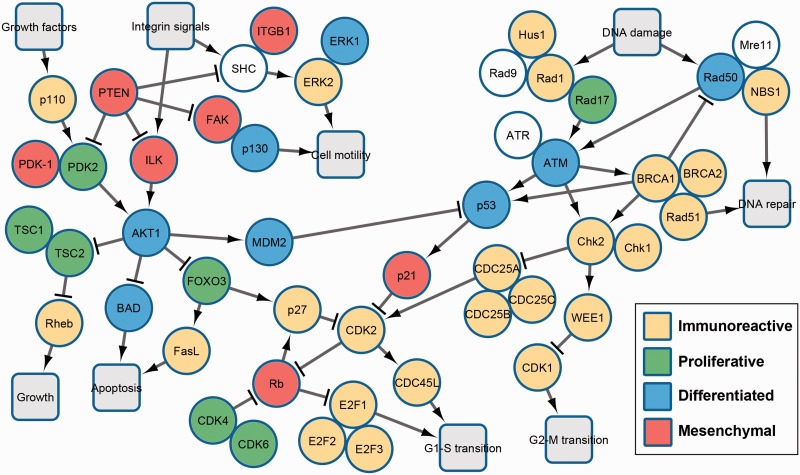
As in our validation step, we assigned genes to modules (I/P/D/M) based on the maximum value within each column of the normalized H_k matrix. Thus, membership to a module means that a gene is most highly expressed in that module relative to other modules. Figure 3 shows the distribution of the modules across multiple cancer-related processes, which include DNA repair (top right), cell cycle regulation (bottom), cell survival and proliferation (left) and cell migration (top left). Visualization was performed with Cytoscape (Cline et al., 2007).

Fig. 3.

Module memberships of genes (from iNMF) arranged according to pathways derived from BioCarta and relevant literature and include processes of DNA repair (top right), cell cycle regulation (bottom), cell survival and proliferation (left) and cell migration (top left) (Color version of this figure is available at Bioinformatics online.)

The DNA repair pathway begins with the Rad9/Hus1/Rad1 and Rad50/Mre11/NBS1 complexes, which sense DNA damage. The signal is transduced via the protein kinases ATM and ATR to checkpoint regulators p53, Chk1 and Chk2 that delay cell cycle progression, as well as to inducers of homologous repair BRCA1, BRCA2 and Rad51 (Houtgraaf et al., 2006; Yoshida and Miki, 2004). Cell cycle progression is managed by CDK2-activated CDC45 (initiates DNA replication), transcription factors E2F (activate S phase progression) and CDK1 (promotes G2-M transition). Also, Rb1 is a tumor suppressor involved in regulating many cellular processes, including G1-S transition, proliferation and differentiation (Giacinti and Giordano, 2006).

In the PI3-Kinase pathway, growth factors activate PI3K, of which p110 is a catalytic subunit and directly opposes PTEN in phosphorylating PIP₂ into the lipid messenger PIP₃. PIP₃ recruits the kinase AKT, which begins a variety of signaling cascades that lead to growth, survival and proliferation. AKT inhibits proapoptotic BAD and growth-inhibiting TSC, as well as activates MCM2, which degrades the cell cycle regulator p53. Phosphorylation of FOXO by AKT retains it in the cytoplasm and prevents its transcriptional activation of cell cycle regulation (via p21) and apoptosis (via FASLG), thus promoting proliferation and survival (Chalhoub and Baker, 2009). Lastly, transmembrane integrin signals activate FAK and SHC, which initiate cell migratory pathways involved in directional migration and random motility, respectively (Yamada and Araki, 2001). Both of these pathways are inhibited by PTEN via dephosphorylation.

By viewing the collection of pathways in light of the module memberships, we see several interesting patterns and connections. Members of module (I) are the most common and are mainly distributed among the DNA repair and cell cycle regulation pathways. This may represent a baseline biomarker signature that is persistent throughout a cell’s life cycle. Members of module (P) are associated, appropriately, with proliferation and survival pathways. Genes in module (D) are more dispersed and participate in a number of processes including checkpoint regulation, survival and cell migration. Finally, genes in module (M) seem to be involved in upstream regulation of cell migration as well as tumor suppression, indicating late stages of tumor development.

It is important to note that our discovered modules do not necessarily equate to subtypes of observations or variables. Although the modules can certainly be used to characterize subtypes as we have shown, there is not necessarily a one-to-one correspondence between the two. For instance, in our above analysis (Fig. 3), module (I) was most highly expressed among many variables, but the distribution of the other modules (P/D/M) may reveal alternative ways to subtype these variables. The modules discovered here describe genomic and observational patterns that additively construct the observed data most efficiently. In this sense, they represent the underlying latent mechanisms that give rise to both observation and variable subtypes but not necessarily the subtypes themselves.

4 Conclusion

As data collection technologies improve and data repositories expand, the quality and accessibility of data from multiple biological sources will continue to grow. As a result, the combined perspectives from internal signatures (e.g. genes, proteins and metabolites) as well as external information (e.g. clinical status, patient history and environmental factors) are contributing to an increasingly rich and complex model of the biological system. However, the abundance and diversity of data is accompanied by the problem of heterogeneity, both in the nature of data sources and in the data collection processes. It is important for strategies of data integration to evolve alongside these new challenges.

We have introduced a novel method of data integration based on a classical matrix decomposition technique. Our method was applied to an integrative study of ovarian cancer, in which we discovered multi-dimensional modules consistent with previously established variable-based subtypes as well as observational clusters. These modules express notable topological patterns among cancer-related pathways, suggesting a connection with underlying biomarker signatures associated with disease subtypes.

The key merits of our approach are as follows. As with jNMF, iNMF is able to detect coordinated signals across multiple datasets. However, iNMF is also equipped to deal with issues arising from heterogeneous data. With its more flexible factorization structure, iNMF is able to adapt to the level of disparity between the datasets, to extract the joint signal of interest from heterogeneous confounders. To distinguish between common patterns spanning multiple sources and distinct patterns unique to individual sources is the first step for developing a proper integration procedure.

The basic framework of iNMF leaves room for further regularization beyond sparsity. One possibility is to consider relationships between individual variables from the same data source (gene-gene interactions) or from different sources (miRNA-gene or DM-gene regulations) (Li and Li, 2008; Zhang et al., 2011). Another approach is to induce adherence to known biological networks or observational relations by means of network statistics. The main challenges are adapting the penalties to the NMF framework and finding effective strategies for tuning selection.

Although our analysis examined several types of genomic variables, our results capture only a snapshot of cancer biology. For future investigations, it may be fruitful to explore more types of genomic data, such as DNA copy number variation and mutation status or even clinical information. It may also be worthwhile to expand the analysis to multiple types of cancers. With the right tools, having a wider selection of data sources will only help in understanding complex disease mechanisms.

Funding

This work was supported in part by the National Institute of Health grants 1R21GM101719-01A1 and U01 CA167234, and the National Science Foundation grants DMS-1161759 and DMS-12-28164.

Conflict of Interest: none declared.