ScaffoldScaffolder: solving contig orientation via bidirected to directed graph reduction

Abstract

Motivation: The contig orientation problem, which we formally define as the MAX-DIR problem, has at times been addressed cursorily and at times using various heuristics. In setting forth a linear-time reduction from the MAX-CUT problem to the MAX-DIR problem, we prove the latter is NP-complete. We compare the relative performance of a novel greedy approach with several other heuristic solutions.

Results: Our results suggest that our greedy heuristic algorithm not only works well but also outperforms the other algorithms due to the nature of scaffold graphs. Our results also demonstrate a novel method for identifying inverted repeats and inversion variants, both of which contradict the basic single-orientation assumption. Such inversions have previously been noted as being difficult to detect and are directly involved in the genetic mechanisms of several diseases.

Availability and implementation: http://bioresearch.byu.edu/scaffoldscaffolder.

Contact: paulmbodily@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Accurate and efficient genome assembly algorithms are essential to unlocking solutions to challenges posed by genetic disease. Insufficient molecular sampling and repetitive regions in the DNA prevent full chromosomal assembly from next-generation sequencing reads, causing assembly algorithms to produce a large set of partially reconstructed chromosomes termed contigs. Contigs must be oriented and positioned to reconstruct full chromosomes using paired-read data to infer positional and orientational relationships between contigs. We define a scaffolding of two contigs as the relative positioning and orientation of contigs weighted by the multiplicity of supporting paired reads.

The problem of scaffolding is often modeled as a graph where vertices are contigs and weighted edges indicate scaffoldings of contigs. The goal in scaffolding is to find a Hamiltonian path that incorporates each non-repeat contig sequence once. As a subtask of scaffolding, the contig orientation problem describes the challenge of assigning each contig a single orientation (as per the single-orientation assumption) so as to minimize conflicting orientation evidence. More specifically, the goal is to remove the minimum number of edges from the scaffold graph, so that the remaining subgraph suggests a single consistent orientation of all vertices (Pop et al., 2004). Solving the contig orientation problem is one step to reducing erroneous linking evidence in the scaffold data.

The contig orientation problem has been equated to the weighted MAX-CUT problem (Dayarian et al., 2010), the bipartite graph problem (Pop et al., 2004) and the odd cycle transferal problem (Donmez and Brudno, 2013). Solutions have included energy cost minimization (Dayarian et al., 2010), a fixed-parameter algorithm (Donmez and Brudno, 2013), mixed integer programming (Salmela et al., 2011), depth-first search (Nijkamp et al., 2010) and greedy bipartite graph coloring (Pop et al., 2004). Several solutions to the more general problem of scaffolding do not explicitly solve the contig orientation problem but provide implicit contig orientation solutions as a result of completing walks through the scaffold graph (Batzoglou et al., 2002; Butler et al., 2008; Li et al., 2010; Zerbino and Birney, 2008).

Formal bidirected graph notation [as first laid out by Edmonds and Johnson (1970)] has a long history in both computer science and bioinformatics research (Edmonds and Johnson, 1970; Jackson and Aluru, 2008; Medvedev et al., 2007; Myers, 2005) but has rarely been employed to represent scaffold graphs (Salmela et al., 2011). Commonly used is a notation in which directed nodes are depicted using some sort of biterminal distinction: one node terminal represents the biological 5^′-end of the contig sequence and the other terminal represents the 3^′-end (Nijkamp et al., 2010; Pop et al., 2004; Zerbino and Birney, 2008). Edges are then connected between the terminals or ends of a node. In this notation, a valid reconstruction or walk through a node requires entering and exiting the node via opposite terminals. The bidirected graph paradigm when applied to scaffold graphs enables new approaches to scaffolding problems, as will be shown.

Research on the MAX-CUT problem has yielded a number of effective approximation algorithms including a min-max cut algorithm (Ding et al., 2001), a randomized linear-time 1/2-approximation (Sahni and Gonzalez, 1976) and branch-and-bound methods (Rendl et al., 2010). Goemans and Williamson (1994) present what is commonly accepted as the best MAX-CUT approximation algorithm (a 0.878-approximation) by randomly rounding the solution to a nonlinear-programming relaxation. Khot et al. (2007) demonstrate that if the unique games conjecture is true, the Goemans–Williamson algorithm is the best possible approximation algorithm for MAX-CUT.

The NP-completeness of the contig orientation problem has not hitherto been formally proven. We provide such a proof, demonstrating the many-one polynomial-time equivalence of the contig orientation and weighted MAX-CUT problems. We present a novel greedy solution and demonstrate its effectiveness compared with several MAX-CUT solutions.

1.1 Contig orientation problem defined

We provide a novel formulation of the contig orientation problem using bidirected graph constructs as a prerequisite to outlining the proof of equivalence with MAX-CUT. A bidirected graph is formally defined as an undirected multigraph G with a set of vertices V and a set of bidirected edges E (Edmonds and Johnson, 1970). A bidirected edge e is a five-tuple $(v_i,o_i,v_j,o_j,w)$ consisting of two vertices, v_i and v_j, the weight of the edge, w, and two endpoint orientations, o_i and o_j, one with respect to each vertex. An endpoint orientation may be either positive or negative, defining e as either positive-incident or negative-incident to the corresponding endpoint.

In the graphical representation of a bidirected edge e, we represent positive-incidence with an arrow pointing out of the vertex and negative-incidence with an arrow pointing in toward the vertex. We thus say that e is directed if it is positive-incident to one endpoint and negative-incident to the other; introverted if positive-incident to both endpoints and extraverted if negative-incident to both endpoints. A directed graph is a special case of a bidirected graph in which all edges are directed edges.

A valid (v₁,v_k)-walk is a sequence v₁,e_1,$\dots ,\hspace{0.17em}{v}_{k-1},\hspace{0.17em}{e}_{k-1}$,v_k where e_i is an edge incident to v_i and v_i + 1 and for all 2 ≤ i ≤ k – 1, $e_{i-1}$ and e_i have opposite endpoint orientations incident to v_i (Fig. 1a and b). Each valid walk through a vertex v_i represents a possible scaffold reconstruction for contig c_i. The contig orientation solution allows for a contig to be included multiple times or in multiple reconstructions while maintaining a consistent orientation (e.g. repetitive sequence).

Fig. 1.

Walks in bidirected graphs. (a) A valid walk enters and exits a node through opposite edge-orientations. (b) An invalid walk enters and exits a node through identical edge-orientations. (c) Reversing all edge-orientations adjacent to a node results in the same valid and invalid walks

We thus define a bidirected scaffold graph for a set of contigs C and a set of weighted scaffoldings F as a bidirected graph $G=$(V,E) in which vertex v_i$\in$ V represents contig c_i$\in$ C and a weighted bidirected edge e = $(v_i,o_i,v_j,o_j,w)$ represents the scaffolding f $\in$ F of contigs c_i and c_j, weighted by the number of supporting paired reads. The endpoint orientations, o_i and o_j, are determined by the relative orientation of the forward strands of c_i and c_j in f—if the forward strands of c_i and c_j are oriented in the same direction, then e is a directed edge that is positive-incident to the vertex representing the upstream contig; if the forward strands are oriented away from one another (i.e. 5′-ends are proximal), then e is an extraverted edge and if the forward strands are oriented toward one another (i.e. 3′-ends are proximal), then e is an introverted edge.

The 5′–3′ directionality of a DNA molecule must ultimately be consistent along the entire length of the sequence. This means that introverted and extraverted edges, both of which represent internally inconsistent 5′–3′ directionality of the forward strand, violate a biological constraint. As per this definition, only directed edges are considered valid in the final scaffold reconstruction. A graph which retains the most weight in directed edges will retain the most internally consistent supporting evidence.

Directed edges can be formed from introverted and extraverted edges by reversing one of the edge’s endpoint orientations. This is essentially what is accomplished when we consider inclusion of the opposite strand of a contig in place of the strand currently being considered for inclusion: all endpoint orientations adjacent to the contig are reversed (Fig. 1c).

The notion of contig orientation is used to more simply refer to which contig strands (relative to the initial forward strands) are being considered in a scaffolding. Thus, in our graph, we will say that for any vertex v_i$\in$ V, we can arbitrarily select between the forward-orientation assignment $v_i^{+}$ and the reverse-orientation assignment $v_i^{-}$. We will refer to this selection as the contig-orientation assignment of c_i or vertex-orientation assignment for v_i. Furthermore, we refer to a contig-orientation assignment for all contigs in C (or vertices in G) as a contig-orientation assignment of C (or vertex-orientation assignment of G). We will refer to a vertex v_i with possible vertex-orientation assignments $v_i^{+}$ and $v_i^{-}$ as an orientable vertex. As the forward strand $c_i^{+}$ of each assembled contig c_i is arbitrarily given as input, each corresponding vertex v_i is initially assumed to be assigned the vertex-orientation $v_i^{+}$.

1.1.1 MAX-DIR problem

We formally state the corresponding decision problem as follows:

MAX-DIR = {(G,k) | G is a bidirected graph with orientable vertices, and there exists a vertex-orientation assignment for G resulting in a subgraph containing at least k directed edges}

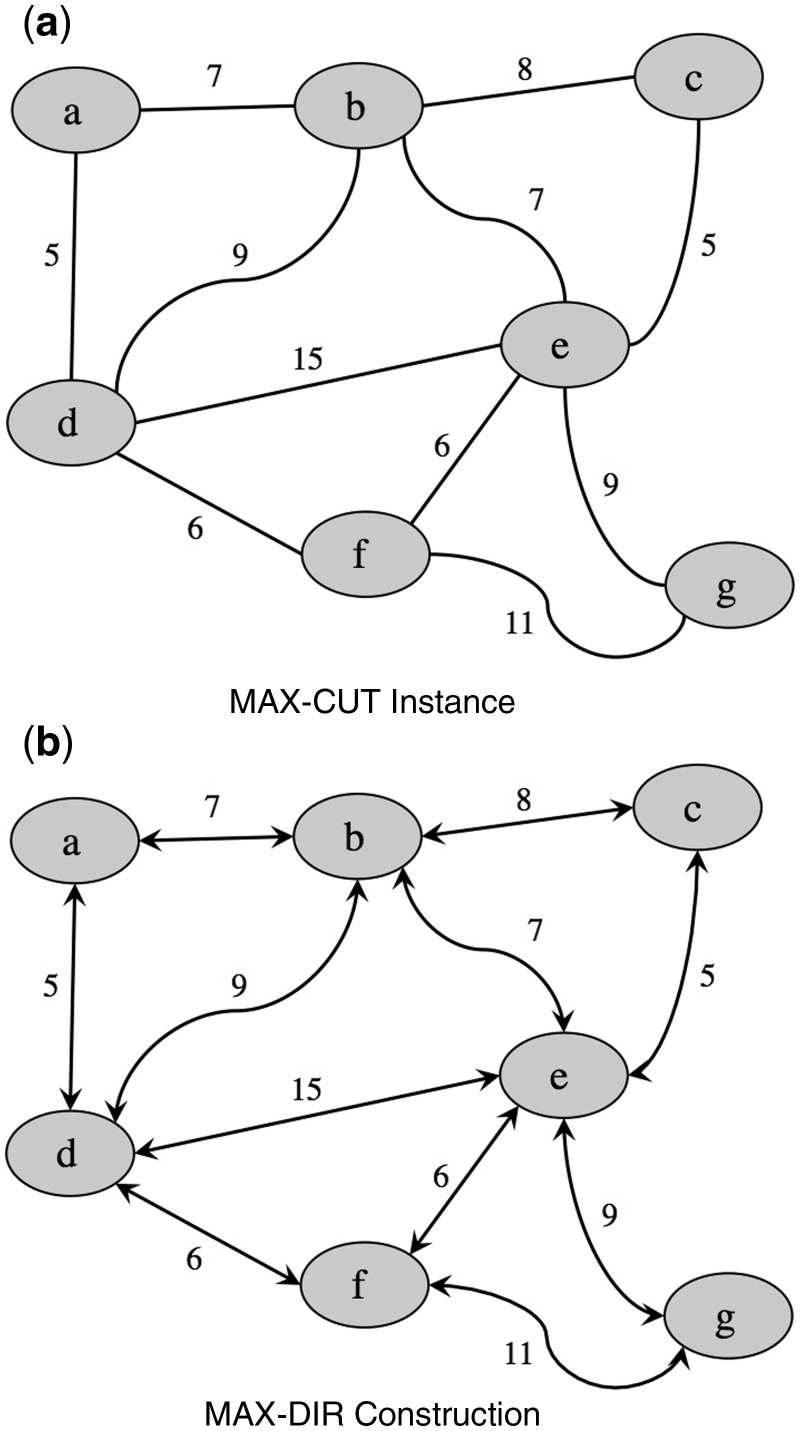
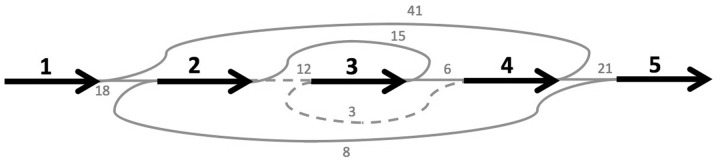
Depending on whether the preferred bias is toward more evidence or more edges, the weighted and unweighted versions of this problem (respectively) become important. In the following equivalence proof of the MAX-DIR and MAX-CUT decision problems, we will consider the unweighted version and assume that the weighted version is readily deducible from the unweighted. The example in Figures 2 and 3 demonstrates the weighted versions of each problem.

Fig. 2.

Fig. 2. An instance of the MAX-CUT problem shown with the reduction to MAX-DIR

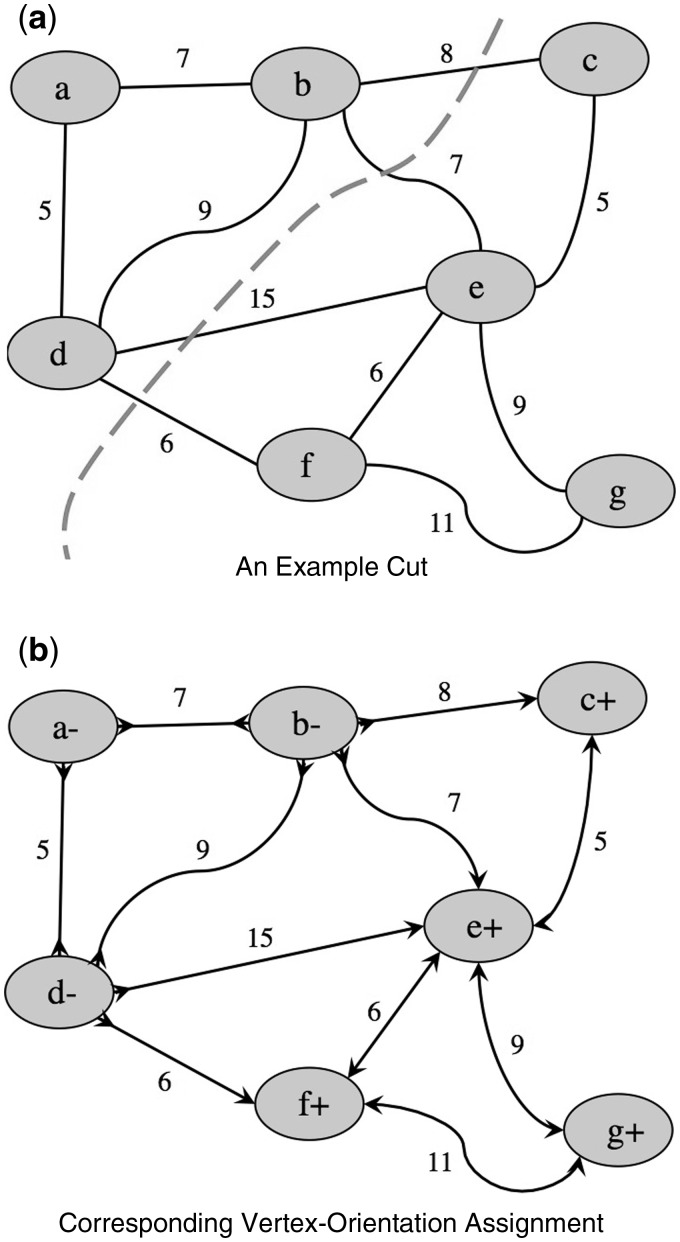
Fig. 3.

A possible cut of the graph in Figure 2a and the corresponding vertex-orientation assignment for the bidirected graph in Figure 2b. Both the weight of the cut and the sum weight of the directed edges are the same. In the subgraph of nodes and directed edges resulting from the vertex-orientation assignment, each contig in any valid walk will be consistently oriented

1.2 Proof of equivalence with MAX-CUT

The proof that MAX-DIR is NP-complete is useful because it signals that a heuristic will likely be required to solve an instance of the contig orientation problem (i.e. the MAX-DIR problem) on any reasonably large input. Because MAX-CUT is NP-complete and MAX-DIR $\in$ NP, it follows immediately that MAX-DIR ${\le }_m^P$ MAX-CUT. The many-one equivalence in polynomial time is useful because it allows us to reduce any MAX-DIR problem to a MAX-CUT problem and then solve it using existing MAX-CUT heuristics (see Supplementary Materials for details of reduction). Thus, rather than ‘reinventing the wheel’ to solve instances of the MAX-DIR problem, one could reasonably apply existing MAX-CUT heuristics to obtain MAX-DIR solutions.

1.2.1 MAX-DIR is NP-complete

Proof —

To prove this statement, we must demonstrate that

1. MAX-DIR $\in$ NP and

2. $\forall L\in$ NP, $L{\le }_m^P$ MAX-DIR.

We prove that MAX-DIR is in NP by noting that given a vertex-orientation assignment to a bidirected graph with orientable vertices and an integer k, we can check in polynomial time whether the assignment yields k directed edges.

To prove that $\forall L\in$ NP, $L{\le }_m^P$ MAX-DIR, we must show that some other NP-complete problem is many-one reducible in polynomial time to MAX-DIR. We demonstrate that MAX-CUT has such a reduction to MAX-DIR.

Recall that the decision problem corresponding to the MAX-CUT problem is as follows:

$$\text{MAX}-\text{CUT}=\left\{\left(M,k\right)|M\hspace{0.17em}\text{is}\hspace{0.17em}\text{a}\hspace{0.17em}\text{multigraph}\hspace{0.17em}\text{with}\hspace{0.17em}\text{a}\hspace{0.17em}\text{cut}\hspace{0.17em}\text{of}\hspace{0.17em}\text{size}\hspace{0.17em}k\right\}$$

where a multigraph M = (V,E) is a graph allowing multiple edges between two nodes and a cut in a graph is a partition of V into two distinct subsets S and T. The size of the cut is the number of edges e $\in$ E which have an endpoint in S and an endpoint in T.

We will describe a polynomial-time-bounded construction that maps an instance (M,k) of MAX-CUT to some bidirected graph with orientable vertices G and positive integer k such that M has a cut of size at least k if and only if G has a vertex-orientation assignment yielding k directed edges. Let V and E be the vertex and edge sets of M and let $V\prime$ and $E\prime$ be the vertex and edge sets of G which we will create. The construction of G from M consists of the following steps (Fig. 2):

1. Let $V\prime$ = V.

2. For each edge e $\in$ E linking vertices v_i,v_j$\in$ V, we create a bidirected edge $e\prime$ linking $v_i\prime$ and $v_j\prime$ (in $V\prime$) where e is negative-incident to both $v_i\prime$ and $v_j\prime$.

Clearly the construction takes polynomial time.

First we show that if M has a cut of size k, then G has a vertex-orientation assignment yielding k directed edges (Fig. 3). If M has a cut of size k, then there is a partition of V into two distinct subsets S and T such that there are k edges which have an endpoint in S and an endpoint in T. By partitioning $V\prime$ into the same subsets, S and T, and assigning forward-orientation to all vertices in S and reverse-orientation to all vertices in T, k bidirected edges (those analogous to the cut edges of M) are rendered directed edges. All others remain either introverted or extraverted edges. It follows from the same line of reasoning that if G has a vertex-orientation assignment yielding k directed edges, then M has a cut of size k.

This completes the proof that MAX-DIR is NP-complete.

2 Systems and methods

Results were collected for nine different algorithms on six different datasets using multiple assessment criteria.

Though several published scaffolding algorithms address the contig orientation problem (Donmez and Brudno, 2013; Pop et al., 2004), none provide sufficient metadata to easily recover their exact contig orientation solution. We thus measure the relative performance of two novel MAX-DIR heuristics (Greedy and RandEdge) and seven other MAX-CUT heuristics as applied to instances of the contig orientation problem:

1. Greedy: Our novel greedy heuristic (see Algorithm 1).

2. RandEdge: Considers edges in a random order and greedily assigns an orientation to adjacent contigs that is consistent with previous orientation assignments (similar to Algorithm 1 except edge e at line 5 is random).

3. BiqMac: A Branch-and-Bound heuristic algorithm for solving weighted MAX-CUT problems which uses SDP relaxation and a relative bound precision criterion (Rendl et al., 2010).

4. LPSolve: lp_solve, a mixed integer linear programming heuristic used by MIP Scaffolder (Salmela et al., 2011).

5. SCIP: A linear-optimization Branch-and-Bound MAX-CUT solver (Achterberg, 2007).

6. GLPK: GNU Linear Programming Kit, a linear/mixed integer programming solver (Makhorin, 2001).

7. SDP: A dual-scaling interior-point algorithm for solving sparse semidefinite MAX-CUT programs (Benson et al., 2000).

8. Sahni: A 1/2-approximation algorithm for MAX-CUT, which adds vertices in random order to maximize the weight of the cut (Sahni and Gonzalez, 1976).

9. Random: randomly orients contigs, retaining edges consistent with assigned orientations (averaged over ten iterations).

Algorithm 1. MAX-DIR Greedy Heuristic

Input: Weighted bidirected graph, G, and min edge weight, w_min

1: Create a forest, F

2: For each vertex $v_i\in G$, add tree t_i to F containing v_i

3: Create a set S of all edges in G with weight w_e > w_min

4: while S is not empty do

5:   Remove an edge e with maximum weight from S

6:   if e connects two different trees, t₁ and t₂, then

7:     add e to F, combining t₁ and t₂ into one tree

8:     if e is not a directed edge then

9:      for all vertices v₂ in t₂ do

10:        Flip orientation assignment of v₂

11:   else if e is a directed edge then

12:     add e to F

13:   else

14:     discard e

15: return F, a weighted directed subgraph

The algorithms were assessed on six scaffold graphs: two synthetic genome scaffold graphs and four real scaffold graphs (see Supplementary Material for details). ScaffoldScaffolder (Bodily et al., 2012) was used to generate scaffold graphs.

1. Synthetic Genome (w/o Errors): A 1.25 Mb diploid genome was synthesized from the zebra finch using HapMaker (Okuda et al., 2013). The following were generated using ART v1.3.1 (Huang et al., 2012): a set of 250 bp reads; a 4 kb paired-end library and a 20 kb paired-end library. Newbler 2.6 was used to assemble contigs. Only 4 kb libraries were used in scaffolding.

2. Synthetic Genome (w/ Errors): Using the 1.25 Mb genome reference, a 200-bp paired-read library was generated from ART. Contig assembly was performed using Newbler.

3. Raspberry Genome: Contigs for the Rubus idaeus cultivar heritage genome were assembled by Newbler using reads from a combination of Illumina HiSeq and 454 sequencing technologies. HiSeq reads were used for scaffolding.

4. Strawberry Genome: Contigs were assembled for Fragaria vesca using Newbler on eleven 454 runs. Two 3-kb paired-end libraries were used to scaffold.

5. Oyster Genome: Contigs for the Pacific oyster Crassostrea gigas were assembled using SOAPdenovo2 (Luo et al., 2012). Paired Illumina reads from 170 bp inserts were used to scaffold.

6. Human Genome: Contigs for HapMap individual NA19240 chromosome X were assembled using SOAPdenovo2. Paired Illumina reads from 550 bp inserts were used to scaffold.

Solutions were assessed on five metrics: the total count of edges retained; the total weight of edges retained; the total count of edges excluded; the total weight of edges excluded and (for real datasets) the computation time required. A contig orientation solution does not produce linear scaffolds. Thus, our evaluative metrics do not include typical scaffold evaluation metrics such as scaffold N50.

3 Algorithm

We developed a greedy heuristic algorithm to solve the weighted MAX-DIR problem (see Algorithm 1). As a heavier-weighted edge generally reflects greater confidence for the scaffolding which it represents, such an edge is likely to be valid, and therefore included in the optimal solution. Thus a greedy algorithm, which maximally favors heavier-weighted edges, approximates an ideal solution for the contig orientation problem.

This algorithm starts by making each vertex in the graph its own tree and then adds edges which combine distinct trees to form larger trees. In combining trees t_i and t_j via edge e, we flip vertex orientations for all vertices in t_j when needed, so that e is always directed. Edges are considered in order of decreasing weight. Any edge e linking vertices v_i and v_j within the same tree t_i is added if and only if, given the current vertex-orientation assignment of v_i and v_j in t_i, e is a directed edge. Additionally, we define a minimum edge weight threshold, w_min, to avoid the risk of determining contig orientation based on erroneous edges with very low support. We ensure that the final subgraph contains solely directed edges by only adding directed edges and ensuring that directed edges remain directed as a result of vertex orientation changes. In cases where two conflicting edges have significant but marginally different weights, there is the danger of discarding biologically significant information. Such cases represent violations of the single-orientation assumption. We consider two such scenarios and their implications below in Section 5.

4 Implementation

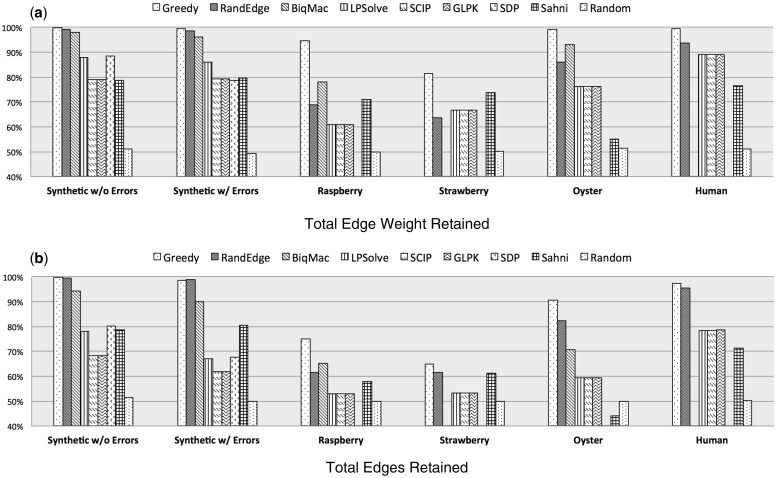
A summary of the total retained edge weight and edge count is shown in Figure 4a and b, respectively (complete results are available in Supplementary Material).

Fig. 4.

Comparative performance of weighted MAX-DIR solutions. In all graphs, the greedy algorithm retained the most total edge support. In general the Greedy algorithm also retained the most edges. The second chart also demonstrates that the RandEdge algorithm’s failure to retain as much total weight as the Greedy algorithm on the real datasets comes (at least in part) as a result of retaining fewer edges. Missing data reflects a failure of the particular algorithm to provide a valid solution for the given dataset

In the synthetic genome graphs, the Greedy and RandEdge algorithms performed best of the compared solutions. The Greedy heuristic retained the greatest number of edges and the greatest total edge weight. We believe that the superior performance of the Greedy and RandEdge algorithms is because these algorithms are designed to greedily include each edge as it is considered, without any concern for solutions that are excluded by its inclusion. Heuristic algorithms generally employ a heuristic function to determine (with some degree of caution) whether or not to include any given edge. In a scaffold graph, the greedy addition of edges (whether considered randomly or ordered by weight) often performs well because most edges are valid and should be included. Therefore, the majority of the supportive evidence should be internally consistent with relatively few spurious edges requiring exclusion.

In many real-world instances of NP-complete problems, the trivial solution is often the wrong solution, thus creating a need for more complex heuristics which bypass the trivial solution. A scaffold graph is quite sparse (i.e. average in- and out-edge degrees are between 1 and 2) and linear by nature, thus rendering the contig orientation problem far more simple than would require a complex heuristic solution. In such a graph, a local optimum will often be part of the global optimum. This serves as a reminder that simply because the complexity of a biological problem can be classified by theoretical computer science does not imply that existing solutions for that class of problem are well-suited to the particular biological application. Domain-specific knowledge is critical to developing algorithms that will work faster and better than existing heuristics.

The Greedy algorithm also outperformed the other algorithms in the scaffold graphs from real datasets. In the raspberry genome graph, the Greedy algorithm retained 17% more total edge weight than the next best algorithm (BiqMac). Likewise in the strawberry, oyster and human graphs, the Greedy algorithm reported margins of 6% and 7%, respectively, above competitors.

On the real datasets, the RandEdge algorithm retained between 13% and 16% less overall weight than the Greedy approach. Despite its average performance, RandEdge is notably faster than algorithms with similar results (see Supplementary Material).

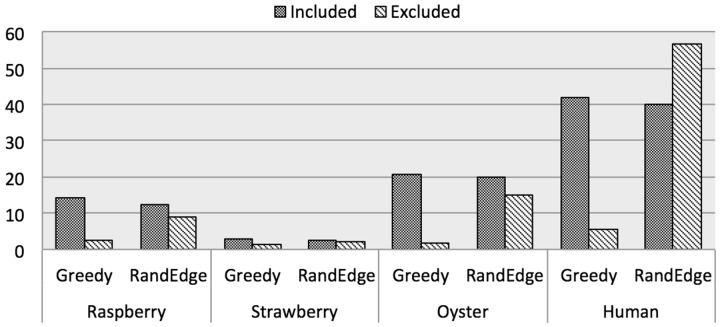
The discrepancy between the Greedy and RandEdge algorithms on real data is largely explained by Figures 4b and 5. The relative decrease in edge weight retention by RandEdge is mirrored in a relative decrease in the number of edges retained. We also find that RandEdge is generally including lighter edges and conversely excluding heavier ones than the Greedy algorithm is. Thus biasing toward the heavy edges not only results in more weight retained but also in more total edges retained. We might expect this result given that the heavy edges are more likely to represent the set of internally consistent edges in the scaffold graph.

Figure 5 also confirms that the greedy algorithm is correctly removing the erroneous edges. Regardless of the overall average weight (i.e. sequencing depth) for a real dataset, the weights of spurious edges tend to maintain a consistent distribution clustered close to 0. The average weights of included and excluded edges, however, vary as a function of the overall average edge weight per dataset. Thus, the penalty for adding erroneous edges in place of valid edges grows larger with an increase in overall average edge weight. (Note in Fig. 4a that though the average retained edge weight increases as a function of the overall edge weight average per dataset, it is most largely affected by the choice of algorithm.)

Fig. 5.

Average weight of included/excluded edges. Although the average weights of included/excluded edges vary as a function of the overall average edge weight, the weight of edges excluded by the Greedy algorithm remains close to 0. This suggests that the Greedy algorithm is excluding primarily erroneous edges

The superior performance of the greedy heuristic algorithm is thus likely due to this key observation about the nature of scaffold graphs—heavily weighted retained edges not only contribute more to total edge support than do lowly weighted edges; they are more likely to be part of the optimal solution. The greedy algorithm thus maximally favors edges which are likely to belong in the optimal solution, which helps to explain why it retains far more edge weight (and many more edges) than other solutions.

5 Discussion

We noted a peculiarity in the subgraph produced using our Greedy heuristic on the synthetic genome without errors—the two excluded edges were both adjacent to contig 591. We also noted that contig 591 has an average sequence depth (a value indicative of the number of nucleotides contributing to the assembly at a given locus) of roughly twice the normal diploid depth, making it a likely candidate for being a two-copy repeat. We used BLAST (Altschul et al., 1997) to find where contig 591 aligned to the known reference. We discovered that it aligned perfectly at two locations and that the two matching sequences were inversions (see Supplementary Material).

This case illustrates that if repeats are not screened, they can present exceptions to the contig-orientation problem and more specifically to the single-orientation assumption. The single-orientation assumption will hold only if the contig represents a sequence which repeats in the same orientation in a scaffold (e.g. tandem repeats).

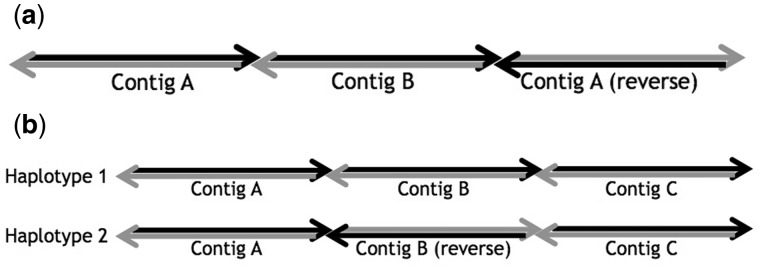
Inverted repeats, like contig 591, represent identical sequences with opposite orientations from two distinct places in a scaffold (Fig. 6a). Among their several biological roles, inverted repeats are used to detect the boundaries of transposons (Rio and Rubin, 1988) and are instrumental in transcriptional regulation (Muskens et al., 2000). Assigning a single orientation to such a contig prevents a viable scaffold reconstruction from occurring, prematurely fragmenting the assembly. This scenario can be resolved prior to assigning contig-orientations by special handling or screening of repeat contigs (Li et al., 2010; Pop et al., 2004). This example shows that in addition to removing erroneous linkages from a scaffold graph, the contig orientation assignment will remove any viable biological scenario that is an exception to the single-orientation assumption. Thus, if the erroneous linkages can be filtered via other means (e.g. minimum support threshold and next-generation error correction), the contig orientation assignment can be used to identify (via exclusion) biologically viable exceptions to the single-orientation assumption.

Fig. 6.

Violations of the single-orientation assumption. (a) In an inverted repeat, a sequence (contig A) is included in the reconstruction twice in opposite orientations. (b) In a polyploid genome, an inverted haplotype is a sequence (contig B) included in opposite orientations on different haplotypes

One other such exception is the case of inverted haplotypes. Many genomes exist as diploid or polyploid organisms, meaning there are two or more versions (termed haplotypes) of the genome in each cell. An inverted haplotype is a sequence, which is identical but oppositely oriented at corresponding locations on analogous chromosomes (Fig. 6b). Such inversions are often biologically significant and have been specifically shown to be associated at times with mental retardation, microdeletion syndrome, renal cysts and diabetes syndrome, epilepsy, schizophrenia and autism (Antonacci et al., 2009; Zody et al., 2008). Most assembly algorithms have not been specifically designed for diploid genome assembly and assume that where multiple haplotypes do exist, they can be readily merged to form a single ‘reference’ sequence. In doing so, inverted haplotype differences are metaphorically ‘swept under the rug’, which is perhaps why biologists have lamented that ‘unlike other types of structural variation, little is known about inversion variants within normal individuals because such events are typically balanced and are difficult to detect and analyze by standard molecular approaches’ (Antonacci et al., 2009).

Just as a contig orientation solution is able to identify inverted repeats, it is also able to identify inverted haplotypes. We developed a module in ScaffoldScaffolder to automatically generate a detailed report of potential inverted repeats and inverted haplotypes. In the module, candidates are internally identified as any contig (i) having at least two connecting edges from at least one end and (ii) which is connected to two or more excluded edges. The candidates can be classified as inverted repeats or inverted haplotypes based on the location of each candidate contig in a probability density function of contig coverage. A special case is a monocontig inversion candidate, which requires that each of two adjacent contigs be linked via edges from both ends of the candidate.

We tested our new predictive module on both synthetic and real data. We first synthesized a diploid genome (heterozygosity rate ≈ 0.2%) containing an inverted haplotype from the zebra finch chromosome 25. We generated error-free reads for assembly with Newbler, and a graph was created using ScaffoldScaffolder. Using our greedy heuristic algorithm, we assigned orientations to the contigs which resulted in a subgraph which excluded 12 edges. The potential inversion report listed three inversions (two with sequencing depth to suggest inverted repeats). We verified that all three inversions were accurate using BLAST and verified that the (non-repeat) inverted haplotype aligned at the expected location in the reference haplotype sequences (see Supplementary Material).

To confirm our ability to predict inverted haplotypes in real data, we identified a 18.7 kb inverted haplotype (HsInv0393) from the Human Polymorphic Inversion DataBase (Martínez-Fundichely et al., 2014) that has been found to be heterozygous in human HapMap individual NA19240 (Aguado et al., 2014). From this individual, we assembled paired Illumina reads mapping to a 64 kb segment of chromosome X in the region of HsInv0393. We created a small graph of the assembled region with ScaffoldScaffolder using the same paired reads. The greedy heuristic algorithm assigned contig orientations, excluding two well-supported edges. The algorithm identified a 9.4 kb inversion, contig 3, that when mapped to the hg19 reference aligned in the region defined for HsInv0393. In addition, the two 4.65 kb contigs scaffolded on either side of this inversion (contigs 2 and 4) were also identified as inverted repeats. This arrangement in the scaffold graph (summarized in Fig. 7) suggests not only that contig 3 is inverted but that possibly some or all of contigs 2 and 4 are also part of the inversion (hence why many inversion breakpoints are reported as ranges). We observe that distinguishing between an inverted haplotype and a non-inverted sequence flanked by inverted repeats is impossible by this approach without pairs that span beyond the inverted repeats (which in the case of NA19240 were unavailable).

Fig. 7.

Scaffold graph of heterozygous HsInv0393 inversion in NA19240. Black arrows are contigs, pointing 5′–3′. Solid lines are putative scaffoldings weighted by paired evidence. Dotted lines are scaffoldings which were excluded by the greedy heuristic. Contig 3 is a potential inversion. Because contigs 2 and 4 are inverted repeats, the exact breakpoints of an inverted haplotype are undetectable

Ongoing development and testing will help to assess the efficacy of this inversion detection method on a larger scale. However, both the theory and our small tests confirm that edges which are excluded in solving the contig orientation problem are suggestive of inverted repeats and inverted haplotypes in de novo assemblies, particularly when such sequences are adjacent to multiple or heavily supported excluded edges.

The contig orientation problem, which we have formally framed as the MAX-DIR problem, has at times been addressed (somewhat apologetically) only cursorily and at times using various heuristics. In setting forth a linear-time reduction from the MAX-CUT problem to the MAX-DIR problem, we have proven that the latter is NP-complete. We have compared the relative performance of our novel greedy approach with several other heuristic solutions. Our results suggest that the greedy heuristic algorithm not only works well, but outperforms the other algorithms due to the nature of scaffold graphs. In such graphs, heavier-weighted edges are more likely to be valid and therefore included in the optimal solution. A greedy algorithm, which maximally favors such edges, approximates an ideal solution. One unanticipated outcome of this study has been the discovery of a novel method for identifying inverted repeats and inversion variants, both of which contradict the basic single-orientation assumption. Such inversions have previously been noted as being difficult to detect and are directly involved in the genetic mechanisms of several diseases. Thus, this method, which we have implemented as a module of ScaffoldScaffolder, has the potential to assist in the automated discovery of biologically significant features in de novo genome assembly.