Table 1. Parameter values for the fit of the displacement distribution with a truncated power law found in previous studies.
| Data source | Trajectories | β | κ | Δr0 |
|---|---|---|---|---|
| Dollar bills33 | 464 K | 1.59 | ∞ | 0 |
| Mobile phones11 | 100 K | 1.75 | 400 km | 1.5 km |
| Mobile phones11 | 206 | 1.75 | 80 km | 1.5 km |
| Mobile phones12 | 3 M | 1.55 | 100 km | 0 |
| Location sharing14 | 220 K | 1.88 | ∞ | 0 |
| GPS tracks27 | 101 | [1.16,1.82] | ∞ | 0 |
| Location sharing15 | 900 K | 1.50 | ∞ | 2.87 km |
| Location sharing15 | 900 K | 4.67 | ∞ | 18.42 km |
| Taxis19 | 12 K | 0 | 4.29 km | — |
| Taxis20 | 7 K | 1.2 | 10 km | 0.31 km |
| Mobile phones13 | 3 M | 0 | [2, 5.8] km | — |
| Travel diaries9 | 230 | 1.05 | 50 km | 0 |
| Tweets17 | 13 M | 1.62 | ∞ | 0 |
| Location sharing16 | 521 K | 0 | 300 km | — |
| Taxis21 | 34 K | 0 | [2, 4.6] km | — |
| Taxis23 | 1,100 | [0.50, 1.17] | [4.5, 6.5] km | 0 |
This list includes studies on different data sources and spatial or temporal scales. Only fits consistent with the function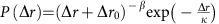 
proposed in ref. 11 are presented here. The case κ=∞ is associated to non-truncated power laws, while β=0 to exponential distributions. When Δr0=0 this parameter was omitted in the fit, and we set β=0 when this value is not defined. Further studies propose: (i) a polynomial form close to an exponential behaviour for private cars24; (ii) two different behaviours for urban and inter-urban trajectories for cars and taxis22,25; and (iii) a lognormal distribution for individual GPS tracks28.