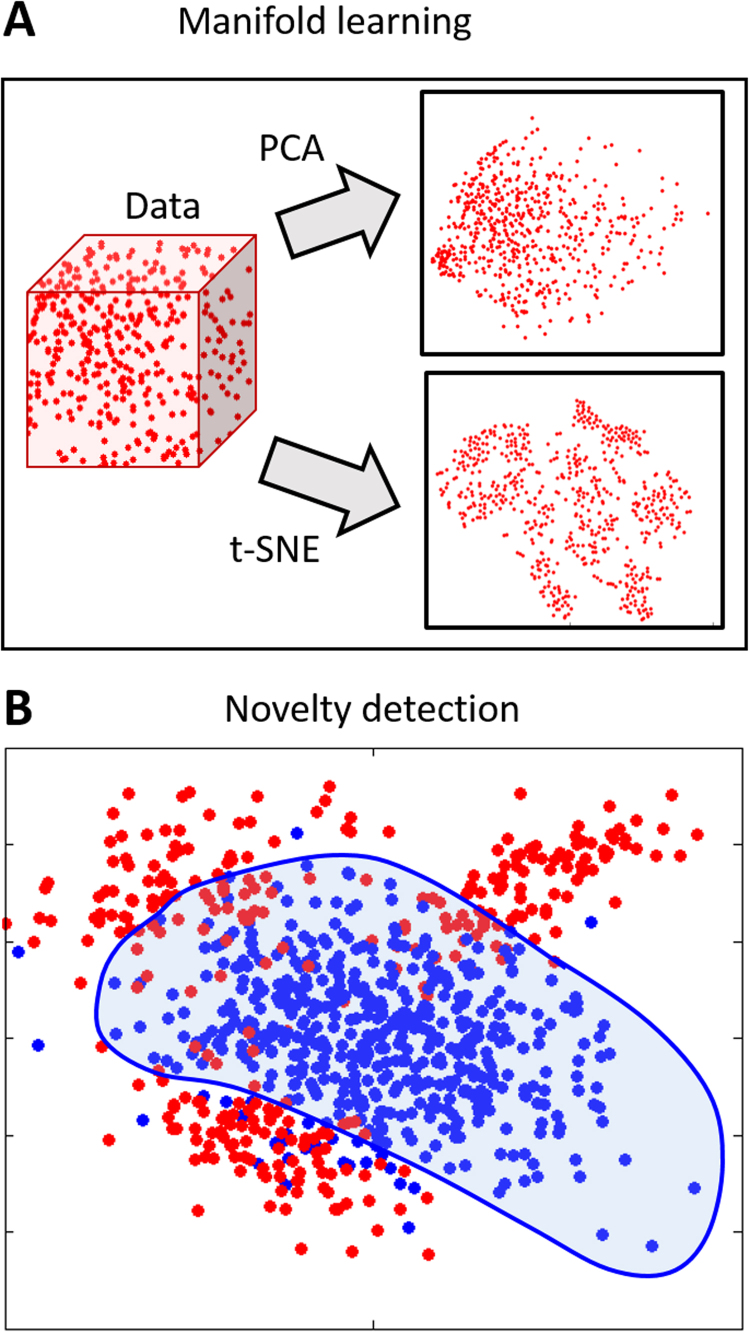
Figure 2.

Schematic examples of alternative approaches to clustering and finite mixture models based on unsupervised learning. (A) Manifold learning techniques aim to find some low-dimensional manifold (right panels) that represent the data more efficiently than the original high-dimensional data (depicted by the cube on the right). Basic dimensionality reduction techniques, such as principal components analysis (PCA), find a single subspace for the data based on maximizing variance. This may not efficiently show structure in high-dimensional data. In contrast, approaches that preserve local distances, such as t-stochastic neighbor (t-SNE) embedding (80), may highlight intrinsic structure more effectively. (B) Novelty detection algorithms, such as the one-class support vector machine (83), aim to find a decision boundary that encloses a set of healthy subjects (blue points), allowing disease profiles to be detected as outliers (red points). Note that this approach does not provide an estimate of the probability density at each point.