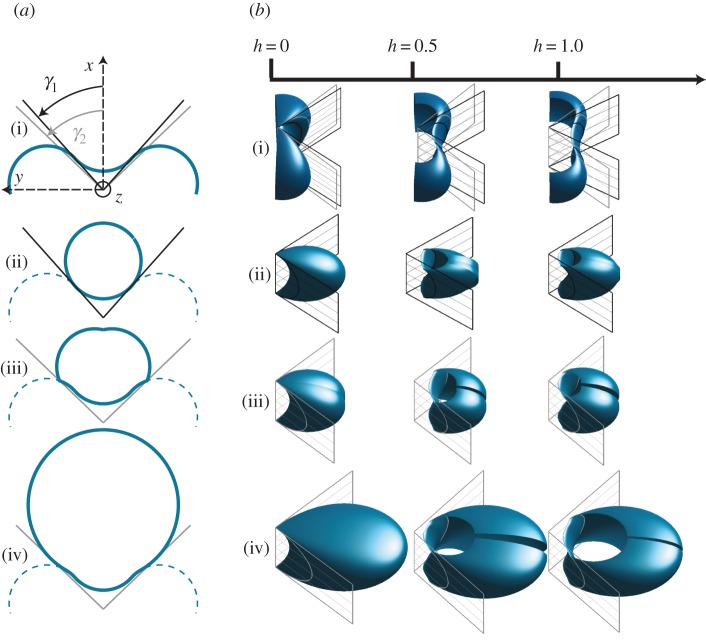
Figure 2.

(a) Each panel (i–iv) represents the z=0-trace, or intersection between the horizontal plane z=0 and a surface of the family at rest state (h=0). Some of the parameters are shared by all the surfaces: R₁=1, α₁=0.7752 and b=1. In each case, we choose $u_{max}=u_{\mathrm{cl},0}$ to close the contour. The trace of the Goursat surface (ϵ=1) is represented by a full-blue line in (i) and by a dashed-blue line in (iii–iv). The black (resp. grey)straight line forming an angle γ₁ (resp. γ₂) with the x-axis correspond to the trace of the black (resp. grey) mirror-plane in the plane z=0: (i) α₁=α₂ and ϵ=1, it is a Goursat surface without fold; (ii) α₁=α₂, γ₁=θ^ϵ(u_fo,1,0)=θ^ϵ(u_jun,1,0), there is no fold as the mirror-plane is tangent to the surface; (iii) α₁=α₂, γ₂=θ^ϵ(u_fo,1,0)> θ^ϵ(u_jun,1,0), there is two folds (located at the intersection between the grey straight lines and the blue contour) as the mirror-plane is not tangent to the surface; (iv) α₁>α₂, γ₂=θ^ϵ(u_fo,1,0)=θ^ϵ(u_jun,2,0), there is no fold as the mirror-plane is tangent to the surface. (b) Family of isometric deformations corresponding to the traces in (a) with c=10 and d=10. The deformation increases from left to right (h=0, 0.5, 1). The black (resp. grey) plane corresponds to the mirror-plane containing the z-axis and making an angle γ₁ (resp. γ₂) with the x-axis. The curves in black (resp. grey) are the intersections of the banana-shaped surface with the mirror-planes. (i) The surface opens with increasing h. (ii) The presence of the fold counteracts the opening at the saddle point. The surface closes on itself while increasing its longitudinal deformation. (iii) As the fold is further away along the surface, the opening dominates the closing effect of the fold. (iv) As the fold is further away along the surface, the opening dominates the closing effect of the fold. (Online version in colour.)