Genetic Structure of Phenotypic Robustness in the Collaborative Cross Mouse Diallel Panel

Abstract

Developmental stability and canalization describe the ability of developmental systems to minimize phenotypic variation in the face of stochastic micro-environmental effects, genetic variation and environmental influences. Canalization is the ability to minimize the effects of genetic or environmental effects, while developmental stability is the ability to minimize the effects of micro-environmental effects within individuals. Despite much attention, the mechanisms that underlie these two components of phenotypic robustness remain unknown. We investigated the genetic structure of phenotypic robustness in the Collaborative Cross (CC) mouse reference population. We analyzed the magnitude of fluctuating asymmetry (FA) and among-individual variation of cranial shape in reciprocal crosses among the eight parental strains, by using geometric morphometrics and a diallel analysis based on a Bayesian approach. Significant differences among genotypes were found for both measures, though they were poorly correlated at the level of individuals. An overall positive effect of inbreeding was found for both components of variation. The strain CAST/EiJ exerted a positive additive effect on FA and, to a lesser extent, among-individual variance. Sex and other strain specific effects were not significant. Neither FA nor among-individual variation was associated with phenotypic extremeness. Our results support the existence of genetic variation for both developmental stability and canalization. This finding is important because robustness is a key feature of developmental systems. Our finding that robustness is not related to phenotypic extremeness is consistent with theoretical work that suggests that its relationship to stabilizing selection is not straightforward.

Phenotypic robustness is generally broken down into developmental stability and canalization, but it is not clear how this distinction maps to the underlying developmental determinants of robustness (Réale & Roff, 2003; Willmore et al., 2005; Pélabon et al., 2010; Breno et al., 2011). Developmental stability refers to insensitivity to internal stochastic perturbations, while canalization is buffering of genetic or environmental variation (Hallgrímsson et al., 2002; De Visser et al., 2003). Canalization thus deals with the extent to which a trait is sensitive to genetic or environmental effects while developmental stability addresses the extent to which a trait is sensitive to internal or micro-environmental noise (Wagner et al., 1997; Hallgrímsson, 1998; Hallgrímsson et al., 2002; Willmore, 2007). In Wagner et al’s (1997) population genetic definition of canalization, the genetic variance of a complex trait is composed of the number and frequency of the genes that influence it as well as the distribution of the magnitudes of effects of those genes. In this model, genetic factors that alter phenotypic variance by the magnitudes of effects at other genes influence genetic canalization. Similarly, genetic factors that alter the magnitudes of environmental phenotypic effects influence environmental canalization (Wagner et al., 1997). An important question that remains poorly addressed is the extent to which these aspects of robustness map to common or diverse underlying developmental determinants (Meiklejohn & Hartl, 2002).

Developmental stability is usually measured using phenotypic deviations from symmetry that are random in direction and normally distributed in magnitude (Van Valen, 1962). In bilaterally symmetric organisms, internal perturbations can be asymmetric, affecting one side and not the other. Such influences can also influence processes that affect both sides. By contrast, genetic effects are more likely to influence developmental processes that affect both sides, although there are certainly examples of asymmetric processes for which there is heritable variation (Palmer, 2004). Environmental effects can produce both symmetric and asymmetric influences, depending on their nature and the scale at which they act (Scharloo, 1991; Hallgrímsson, 1998). Factors affecting the whole organism such as temperature or nutrition are most likely to influence processes that affect both sides equally. Thus, although the among and within-individual phenotypic variances do not cleanly demarcate canalization and developmental stability, understanding the extent to which these two components of phenotypic variance share genetic architecture is important for understanding the developmental basis for variation in phenotypic robustness.

Finally, it is not well understood how phenotypic robustness evolves (Pélabon et al., 2010; Pavlicev & Hansen, 2011; Rouzic et al., 2013). Phenotypic robustness is thought to contribute to tolerating mutational loads, which in turn contributes to the accumulation of hidden genetic variation that can be revealed to selection under changed environmental conditions or mutations with large effects, leading to episodes of rapid evolution and divergence (Hermisson & Wagner, 2004; Flatt, 2005; Rohner et al., 2013). Schmalhausen (1949) suggested that natural selection favours mechanisms that allow organisms to resist the effects of environmental insults while maintaining the capacity to respond to environmental change. Previous studies have associated aspects of robustness with heterozygosity (Lerner, 1954: Leary et al., 1983; Mitton, 1995; Messier & Mitton, 1996) and with phenotypic extremeness (Soulé, 1982; Clarke, 1995), although these relationships have been difficult to disentangle in natural populations. If robustness evolves by stabilizing selection, then genotypic values further from the mean must be associated with lower robustness.

The Collaborative Cross (CC) mouse reference population (Churchill et al., 2004), which is specifically designed to represent variation occurring in natural populations, provides an opportunity to study the genetic structure of phenotypic robustness in a system that maximizes controlled genetic variation. The Collaborative Cross project creates new lines of mice derived from eight genetically and phenotypically diverse founder strains (five inbred and three wild-derived) that represent three Mus musculus subspecies (Svenson et al., 2012). These derived lines provide high resolution for quantitative trait locus (QTL) mapping, and have been used to study a variety of complex phenotypic traits (Durrant et al., 2011; Shusterman et al., 2013). Despite the potential of the CC mice for exploring the developmental genetic structure of phenotypic robustness, the buffering capacity of the CC founders remains largely unexplored.

The CC founder strains and their reciprocal crosses form a nearly full diallel design (Jinks & Hayman, 1953; Lenarcic et al., 2012) consisting of 62 crosses (54 heterozygous and 8 homozygous). This design allows characterization of the average contribution of each parental group to the phenotype, as well as the effect of specific combinations of alleles and sex on FA and among-individual phenotypic variation. Individuals within CC parental lines and their F1 crosses are genetically identical (apart from spontaneous mutations), and all strains were bred under uniform conditions. For this reason, we assume that the phenotypic variation within groups reflects only environmental variation (associated with uncontrolled factors such as the position in the uterine horns, litter size, etc.), while variation among strains is genetic. This allows us to obtain both a measure of developmental stability, via fluctuating asymmetry, and canalization, via relative magnitudes of within-group variance, for each of the 8 parental strains and 54 heterozygous crosses.

We use the CC diallel to study developmental stability and canalization of skull morphology. The skull has been widely used in studies of phenotypic robustness because it provides a relatively simple system for assessing developmental stability and canalization through their effects on morphology. Specifically, we test four related hypotheses about the genetic architecture of phenotypic robustness:

1. That there is genetic variation for both canalization and developmental stability in the CC panel.

2. That the genetic variation in these two components of robustness correspond across the diallel panel.

3. That parental strains and F1 crosses differ in FA and within-group variance.

4. That FA and within-group variance increase away from the mean genotypic values for craniofacial shape across the diallel panel.

Together, these four hypothesis tests are significant for understanding the genetic architecture of robustness. Hypothesis 1 and 2 address the extent to which there is genetic variation in robustness and to what extent developmental stability and canalization map onto the same or different processes. Hypotheses 3 and 4 uniquely disentangle the extent to which robustness varies with heterozygosity versus phenotypic extremeness, thus testing a critical prediction of the larger hypothesis that robustness evolves via stabilizing selection.

Material and Methods

Animals

This study was performed on a reciprocal diallel cross consisting of eight inbred strains and an almost complete set of their F1 crosses (see below). The parental strains are the founders of the Collaborative Cross (Chesler et al., 2008; Threadgill & Churchill, 2012), and include five inbred strains (A/J, C57BL/6J, 129S1/SvImJ, NOD/ShiLtJ, and NZO/HlLtJ) and three wild-derived (CAST/EiJ, PWK/PhJ, and WSB/EiJ), which are representative of the three major Mus musculus subspecies (Mus musculus castaneus, Mus musculus domesticus and Mus musculus musculus). Overall, they capture 90% of genetic variation of laboratory mice (Threadgill & Churchill, 2012). The parental strains will be denoted here by letters A-H for simplicity (Table 1). Mice of F1 generation were housed 2–5 animals per cage and had unlimited access to standard laboratory chow (LabDiet 5K52) and acidified drinking water. Individuals were sacrificed at an average age of 72 days. The sample analyzed comprises 15 to 25 animals of both sexes per group with a total sample size of 1211 animals (Table S1). Due to breeding incompatibility, the EF and EG crosses are not represented in the sample.

Table 1.

List of strains used as parentals in the diallel crosses.

Code	Short Name
A	A/J
B	C57/BL6
C	129S1/SvImJ
D	NOD/ShiLtJ
E	NZO/HILtJ
F	CAST/EiJ
G	PWK/PhJ
H	WSB/Ei

Morphometric analysis

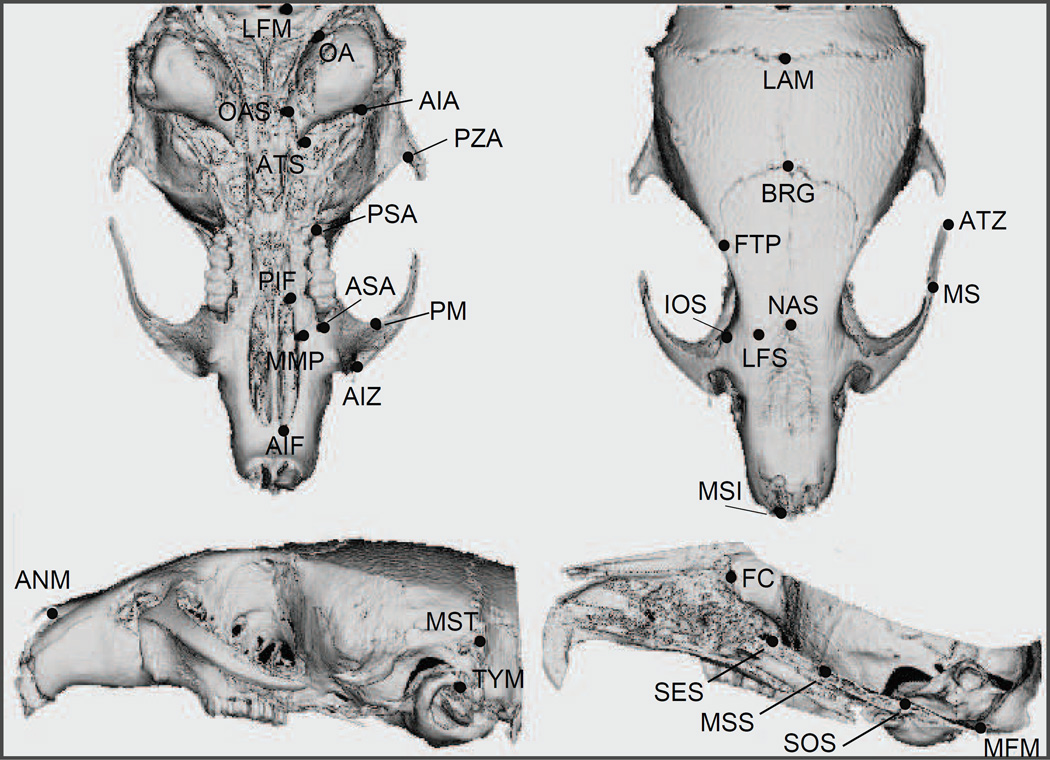
All crania were scanned by micro CT (Scanco V iva-CT40, Scanco Medical AG, Basserdorf, Switzerland) at 35-µm resolution (70 kv, 160 mA, 500 projections). Fifty-four three-dimensional landmarks, shown in Figure 1, were digitized from the 3D reconstructions using Analyze 3D (http://www.mayo.edu/bir/); a detailed definition of the landmarks used is given in Table 2 of Supplementary Material. Paired landmarks were digitized on both sides of the skull to obtain the symmetric and asymmetric components of shape. All skulls were digitized by the same operator to avoid inter-observer error.

Figure 1.

Landmarks digitized on the skull.

The landmark configurations of all specimens from the parental groups and F1 groups were aligned to a common coordinate system by a generalized Procrustes analysis. This procedure translates the specimens to a common origin, scales them to unit centroid size (CS), and rotates the landmark configurations by minimizing the total sum of squared deviations of every landmark configuration from the mean configuration (Rohlf & Slice, 1990). The coordinates of the superimposed landmark configurations are referred to as shape coordinates as they only contain information on the shape of the configurations.

Measurement Error

To estimate the repeatability of the landmarks, we collected two repeated measurements on 16 mice from different groups (including parentals and F1). We then performed a two-way MANOVA on the superimposed landmark configurations (referred to as Procrustes ANOVA) with the individual and the side as factors. Shape variation is thus decomposed into variation across individuals, variation among sides (directional asymmetry) and variation due to an individual-side interaction (fluctuating asymmetry). When repeated measures are taken this test allows evaluation of whether FA is larger than the measurement error, which is estimated as the residual variance. The Procrustes superimposition and the Procrustes ANOVA were performed in MorphoJ 1.05 (Klingenberg, 2011). In addition, we used a two-way ANOVA to test for the effect of side and the side*individuals interaction on cranial size. We used centroid size, or the square root of the summed squared distances of each landmark from the mean of the x,y,z coordinates for each configuration, as a measure of size for the left and right sides. Only paired landmarks were included for these estimation of centroid size.

Fluctuating asymmetry

The asymmetry in the shape of configurations of landmarks was used as an estimation of developmental instability in skull shape. The procedure for extracting the asymmetric component of skull shape of each specimen involves the following steps: 1) each landmark configuration is reflected and the labels of corresponding paired landmarks are exchanged; 2) all the original and reflected configurations are superimposed by a Procrustes analysis. The Procrustes fit produces an average shape between the original and reflected configuration which is perfectly symmetric; 3) for each configuration, the difference between the original and the symmetric consensus is taken as a measure of individual total asymmetry. The sample mean of these differences, i.e., the average pattern of total asymmetry, is referred to as directional asymmetry, and the individual variation of total asymmetry around this mean is referred to as fluctuating asymmetry (Mardia et al., 2000).

To test for differences in FA between parental groups and evaluate the effect of heterozygosity on FA, we quantified asymmetry of skull shape for each specimen as the deviation of an individual´s total asymmetry in skull shape from the average asymmetry in units of Procrustes distance (Klingenberg & McIntyre, 1998; Klingenberg & Monteiro, 2005). This landmark based index (called here FA shape score) is calculated as the square root of the sum of squared distances between each pair of corresponding landmarks in the individual and mean a symmetric configurations. Because systematic variation in directional asymmetry can bias the estimations of FA (Stige et al., 2006), we first tested between-group differences in directional asymmetry by applying a MANOVA on the principal component scores of the asymmetric component with genotype as the predictive variable. The PC scores were obtained using the function procSym in the package Morpho for R (Schlager, 2015). If significant differences were detected, the FA scores were estimated as the square root of the sum of squared residuals from the asymmetric configuration of each specimen and its group asymmetric mean (Stige et al., 2006). Then, differences in FA between groups were evaluated using a one-way ANOVA test on the FA shape scores using genotype as the main factor.

The magnitude of size FA was assessed by computing separately the centroid sizes of the left and right sides of the skull. Then, an index of asymmetry (called here FAcs) was calculated for each specimen as the absolute value of the difference between the sizes of both sides of the skull. This index provides an individual estimate of the magnitude of asymmetry, and the mean of absolute differences provides an estimate of the variance of R – L in a group of specimens (Palmer & Strobeck, 2003; Zachos et al., 2007). Consequently, the homogeneity of variance among samples can be assessed by an ANOVA on the absolute deviations (i.e., Levene’s test for differences in variance). In this sense, this univariate index is similar to the multivariate FA shape score used here (Klingenberg & McIntyre, 1998). Moreover, in one dimension the distance between two points is the absolute value of their numerical difference, which is the same as estimating the square root of the squared difference between the two points. Because significant directional asymmetry (DA) in size was detected (i.e., the average of the signed difference between sides (L-R) for each skull across specimens within parental and F1 groups was non-zero) the FAcs index was calculated as |(L-R)-DA|. We chose this FA index for comparability to previous studies (Hutchinson & Cheverud, 1995; Carter & Houle, 2005). The scores of asymmetry in cranial size (FAcs) were then compared among groups by an ANOVA test in which genotype was the main fixed factor.

Among-individual phenotypic variation

The magnitude of phenotypic variation of the symmetric component among specimens was used as a measure of canalization. The average of a landmark configuration and its superimposed reflection has a perfectly symmetric shape, and symmetric shape variation can thus be computed as the sample variance of these symmetric configurations (Mardia et al., 2000; Klingenberg et al., 2002). Here, the square root of the sum of squared distances between corresponding landmarks of each symmetric configuration and the symmetric group mean (i.e, an estimate of the Procrustes distance) was used to quantify the individual symmetric deviations from the group mean. To test whether the amounts of variation differed among groups, we calculated an ANOVA of the individual deviations from the respective group averages, an extension of Levene's test for multivariate data (Van Valen, 2005).

To assess the association between measures of developmental stability and canalization, we computed the product-moment correlations between the FA shape scores and the magnitude of within-group variation. These correlations were computed using both the scores for each specimen and the values averaged by group.

The direction of main shape variation in FA and within-group variation were compared among the 8 parental groups by estimating the angle between the first eigenvector of either the covariance matrices of individual*side effects obtained from ANOVA Procrustes tests for each parental group or the within-group covariance matrices on the symmetric component. The angles were assessed by comparing them to angles between pairs of random vectors using the procedure implemented in Klingenberg & Marugán-Lobon (2013). The null hypothesis to be tested is that vectors have random directions. If the hypothesis is rejected, the patterns of FA are more similar than expected from random variation. To visualize both patterns of variation in shape, landmark configurations displaying the shape changes along the first PCs were used to morph a consensus skull surface into the positive extreme of variation (Wiley et al., 2005) using Landmark (http://www.idav.ucdavis.edu/research/EvoMorph). Both surfaces were kept aligned with their original axes and their differences were computed using Hausdorff distances, implemented as a filter in MeshLab (Visual Computing Lab -ISTI-CNR, http://meshlab.source.forge/). A colormap representing the differences between shapes was then constructed using the Color filter in MeshLab.

Genetic structure of among-individual variation in symmetric component and FA

To assess whether the differences in phenotypic variability between lines can be assigned to the additive effects of alleles, or whether they are context-dependent effects modified by the particular genetic background, sex, or parent, we performed diallel analysis using the R package BayesDiallel (version .851 (Lenarcic et al., 2012); (http://valdarlab.unc.edu/software.html). This univariate Bayesian approach provides a framework to estimate standard additive genetic effects on a trait in diallel data, as well as non-additive effects such as dominance, maternal, strain and sex-specific effects. Each effect corresponds to a parameter in the diallel model, and the method applies MCMC Gibbs sampling procedure to estimate posterior distributions for the following parameters: 1) general effects: include the inbreeding penalty (“inbreed.overall”), strain-specific effects of additive genetics (“additive”), inbreeding (“inbreed”), and parent-of-origin effects (“maternal”); 2) strain pair-specific effects: include effects peculiar to specific strain pairs; 3) sex-specific effects: include sex-specific deviations of the general effects; and 4) sex/strain pair specific effects: comprehend sex-specific deviations from the strain pair-specific effects.. This approach was specifically developed to analyze diallel crosses of inbred lines (Lenarcic et al. 2012). The individual phenotypes analyzed were the FA scores and the scores for the symmetric deviation from the mean (Réale & Roff, 2003). The corresponding genetic effects on the mean values of the cranial traits are described in Percival et al. (2015).

Results

Fluctuating asymmetry

Given that differences between left and right sides of the same specimen are expected to be small, it is important to compare them against measurement error. The results of the Procrustes ANOVA in a subsample of 16 skulls showed that measurement error was lower than shape differences between sides within individuals, as shown by the significant value found for the individual-side interaction (Table 2). This means that true FA can be detected, although the effect of ME increasing the estimated FA values cannot be completely discarded. Because all specimens were scanned with the same protocol and landmarked by a single trained observer, the main source of measurement error is attributed to random variation due to intra-observer error. Consequently, the ME can be assumed to be equal across strains. This test also revealed the presence of directional asymmetry for skull shape as shown by the significant values found for the side effect. Similar results were obtained for skull size, for which individual differences between sides were larger than measurement error (Table 2). The presence of directional asymmetry in size was also detected as displayed by the significant side effect.

Table 2.

Analysis of measurement error for shape variables and centroid size.

Effect	SS	MS	df	F	P
Shape
Individual	0.049720	0.000041	1215	8.77	<.0001
Side	0.003495	0.000047	74	10.13	<.0001
Individual × Side	0.005178	0.000005	1110	3.18	<.0001
Measurement Error	0.003638	0.000001	2480
Size
Individual	172701	11513	15	3037.76	<.0001
Side	997	997	1	263.08	<.0001
Individual × Side	334	22	15	5.88	<.0001
Measurement Error	121	4	32

Significant departures from symmetry were detected for cranial size in most of parental and F1 groups, being the left side larger than the right. Thus, the effect of directional asymmetry was taken into account in the estimation of FA scores for size. Because directional asymmetry in size was similar across groups, FA scores for each specimen were estimated as the departure of individual asymmetries from the mean sample asymmetry. The comparison of the FAcs scores corrected by directional asymmetry showed no significant differences (P=0.108) across all groups (including parentals and F1). Therefore, no further analyses were performed for skull size.

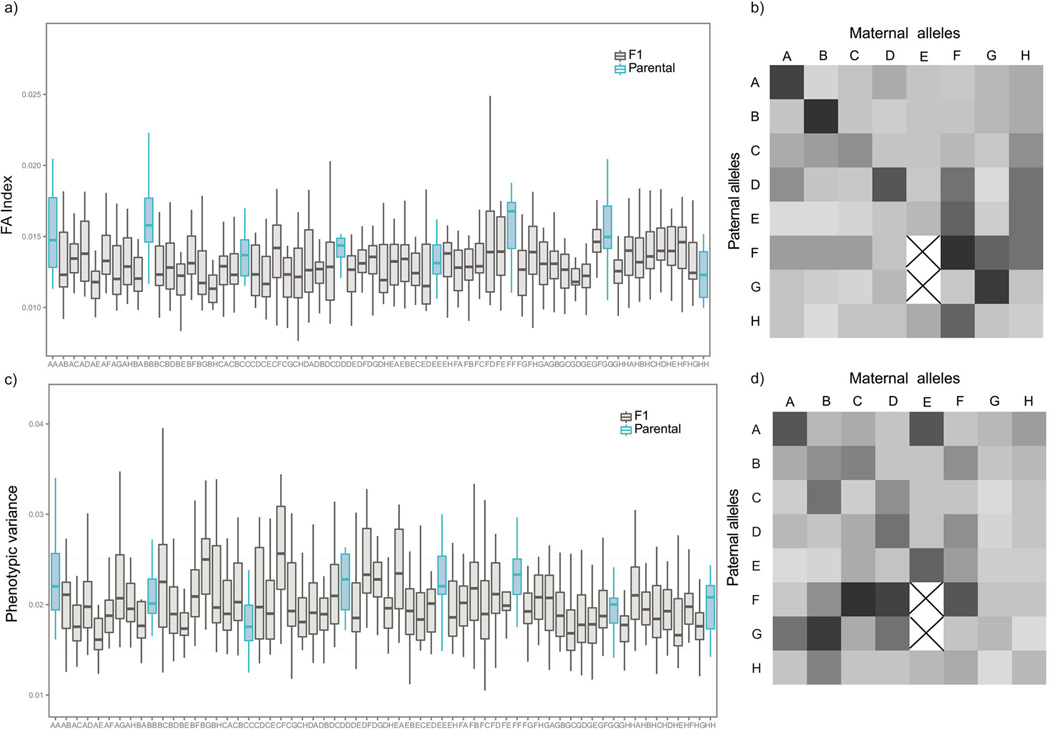
Conversely, the results of the MANOVA on the PC scores of the asymmetric component showed significant differences among groups (Pillai's Trace = 1.66, F_61,1149 = 2.18, P=2.2e-16) indicating variation in directional asymmetry. The FA scores for shape corrected by directional asymmetry displayed differences in the amount of FA among parental strains (F_7,132=5.39, P=1.85e-05). Particularly noticeable was the increase in FA values in AA (A/J), BB (C57BL/6J) and FF (CAST/EiJ) groups, and the low value observed in the HH (WSB/EiJ) group (Figure 2a). Significant differences were also found among F1 groups (F_53,1017= 1.893, P=0.000166).

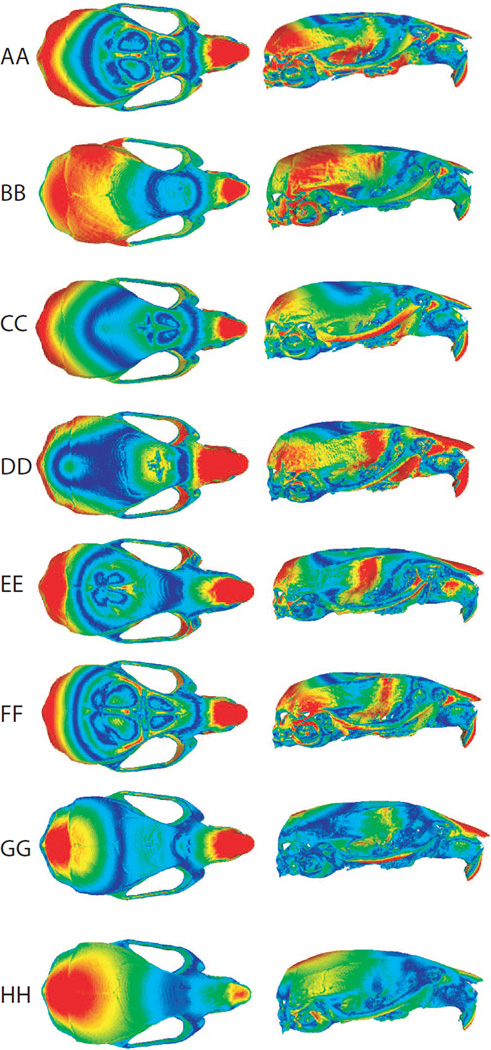
Figure 2.

Box plots and heatmaps showing average scores of shape fluctuating asymmetry (a, b) and within-group variation (c, d) for the parentals and the diallel crosses. The intensity of color in the heatmap represents the magnitude of average asymmetry (b) and the mean of the distances of each specimen to the group mean (d) for each group.

Parental groups not only differed in the magnitude but also in the pattern of fluctuating asymmetry, as shown by the angles between the first eigenvectors of the covariance matrices of individual*side interaction effects obtained from ANOVA Procrustes tests for each parental group (Table 3). The pattern of asymmetry in each parental group is visualized in Figure 3. In most groups, the asymmetry is mainly localized at the superior and lateral views of the maxillary bone, as well as the inter-parietal and temporal bones, while the cranial base displays the lowest asymmetry. The results of the angular comparison suggest that even though the fluctuating asymmetry of the skull is similarly localized in the eight parental groups, there are differences in the specific patterns of shape variation associated to FA.

Table 3.

Angles between first eigenvectors of covariance matrices of individual-side interaction (upper diagonal) and within-group variation (lower diagonal).

	AA	BB	CC	DD	EE	FF	GG	HH
AA	0	82.064	61.033*	65.495*	63.804*	85.014	57.069*	69.357*
BB	53.339*	0	69.807	77.642	77.633	81.933	64.786*	83.485
CC	33.995*	41.497*	0	61.535*	86.169	80.99	36.874*	88.298
DD	41.46*	48.123*	39.832*	0	69.678*	88.188	58.676*	80.794
EE	59.907*	48.84*	52.755*	55.121*	0	89.253	82.358	68.494*
FF	37.827*	50.904*	34.42*	41.28*	52.929*	0	87.431	77.168
GG	50.213*	55.303*	53.365*	43.768*	52.358*	53.808*	0	89.261
HH	45.781*	48.34*	46.968*	47.107*	51.895*	50.128*	48.33*	0

^*P < 0.05 angles significantly different from expected by random vectors.

Figure 3.

Visualization of shape changes toward the positive scores of the first principal component analysis from the covariance matrix of the individual-side effect. The colorbar represents the magnitude of asymmetry, reddish colors indicate higher differences between the symmetric mean shape and the asymmetric shape along PC1. Note that the colormaps were obtained by interpolating to the entire surface the shape changes captured by 54 landmarks.

The association between FA and centroid size between groups was explored using the mean values of FA scores and centroid size of each group. The analysis was performed for parental and F1 groups separately because there are significant differences in size, with the heterozygous groups being larger than homozygous (Percival et al., 2015). Due to the covariation between these two variables (size and heterozygosity), the effect of size can not be evaluated independently in an analysis that combines parental and F1 groups. Mean FA and mean centroid size had a negative and low association between crosses in both parental and F1 strains (r= −0.103 and r= −0.109, respectively). Low values of association were consistently found when the association was investigated among individuals for each strain separately (results not shown).

To test whether there is a relationship between FA and phenotypic extremeness across the F1 crosses, we computed the correlation between mean FA shape scores by group and the Procrustes distance between the symmetric mean of each F1 group and the grand mean. The association between these two variables was low and non-significant (r=−0.037).

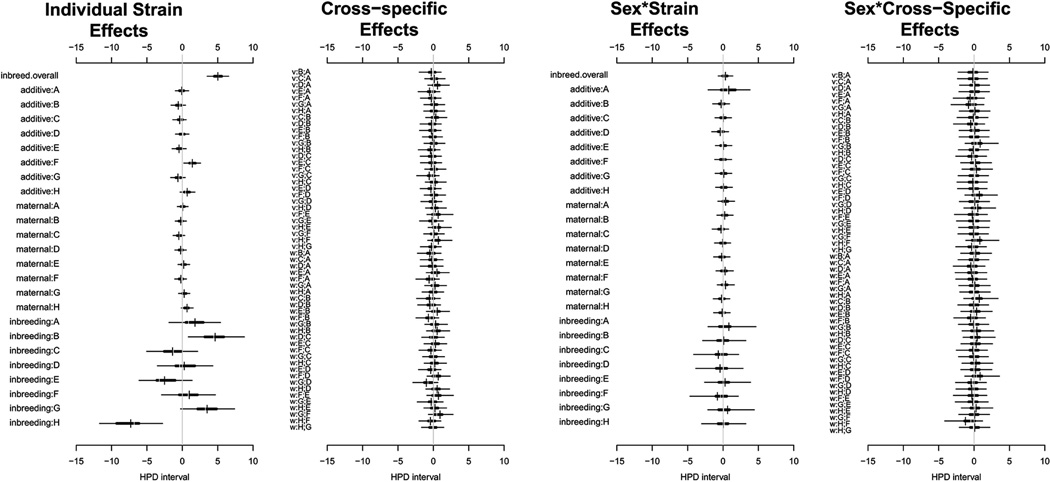
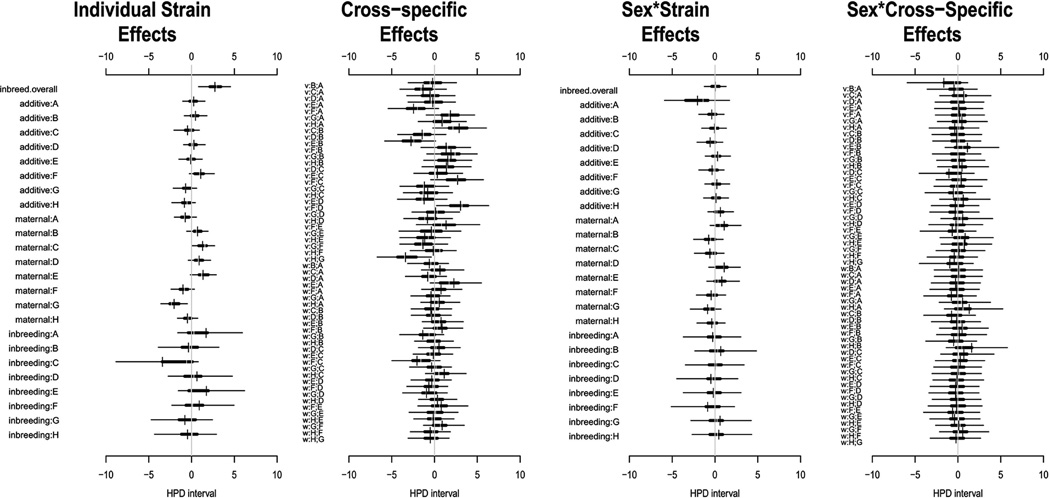
We found significantly higher levels of fluctuating asymmetry in the inbred parental strains (Figure 4), suggesting the overall positive effect of inbreeding on FA. The positive effect of inbreeding in a particular strain is detected as a stronger than expected reduction in FA relative to parental strain. Our expectation is that the F1 manifests an intermediate level of FA between the parental strains. Conversely, a negative effect of inbreeding would manifest as increased FA in the F1. Consistent increase or decrease of FA across different haplotype combinations allows attributing such effects to a particular haplotype. These effects are most notable in strain B (strain C57BL/6J) with increased FA (i.e. reduction in most combinations), and conversely in strain H (WSB/Ei) with low FA, as seen in the lower part of this plot. There is a positive additive effect of the allele F on FA (from the strain CAST/EiJ). The effects of allele combinations on asymmetric deviations from the mean values are shown in the second plot and are effectively absent. The third and fourth plots of the panel are equivalent to the first two plots but show the effects of sex on the additive, inbreeding and epistatic effects. These non-additive effects do not affect the degree of FA in this diallel.

Figure 4.

Highest posterior density (HPD) intervals for effects parameters fitted to the scores of fluctuating asymmetry in skull shape. Horizontal bars show for each parameter the region of highest posterior density that covers 50% (thick line) and 95% (thin line) of the posterior probability. The first panel includes general effects (inbreed overall, strain-specific effects of additive genetics and inbreeding, and maternal effect), the second panel includes effects peculiar to specific strain pairs, the third panel accounts for sex-specific deviations of the general effects, and the fourth panel encompasses sex-specific deviations from the strain pair-specific effects. The “v” and “w” labels in the second and fourth graphs refer to symmetric and asymmetric effects.

Among-individual phenotypic variation

Parental strains and F1 groups differ in the magnitude of phenotypic variation of symmetric component of shape, measured as the average Procrustes distances between specimens and the symmetric consensus of their respective groups (Figure 2b). The ANOVA test showed significant differences among the eight parental strains (F_7,132= 3.681, P= 0.00115) as well as the F1 groups (F_53,1017=3.106, P= 3.91e-12). Among parental strains, the CC (129S1/SvImJ), GG (PWK/PkJ) and HH (WSB/EiJ) groups exhibited the lowest internal variation for the symmetric component of skull shape. The average distance of the symmetric configurations to the mean was not associated with mean centroid size for each group.

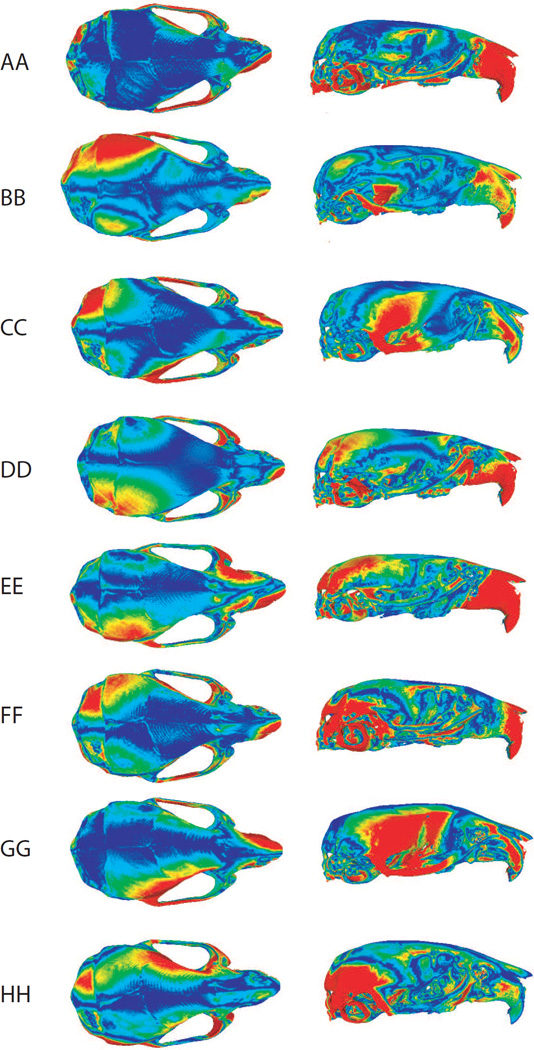
The angles among the first eigenvectors of the within-group covariance matrices of the symmetric component of shape for the parental groups were significantly smaller than between pairs of random vectors (Table 3). This suggests that the patterns of shape variation among individuals captured by the first component are significantly correlated among the 8 parental strains. The covariance matrices were also pooled by sex to account for differences among individuals related to sexual dimorphism. Figure 5 depicts the pattern of shape changes in the within-group variation of the symmetric component as obtained from the principal component analyses of the within-strain covariance matrices. The areas that display the largest symmetric shape changes are the nasal and interparietal bones. This pattern overlaps only partially with the regions that displayed more asymmetry.

Figure 5.

Visualization of shape changes toward the positive scores of the first principal component analysis from the within-group covariance matrices of the 8 parental strains. The colorbar represents the magnitude of differences between the mean shape and the surface that represents the shape changes on PC1. Reddish colors indicate higher differences. Note that the colormaps were obtained by interpolating to the entire surface the shape changes captured by 54 landmarks.

The genetic components of among-individual phenotypic variance in the diallel is visualized in Figure 6. Plot 1 of this figure reveals an overall positive effect of inbreeding on variation. However, the inbreeding effects due to single alleles are less consistent, as seen in the lower part of this plot. Additive effects of single alleles on this measure of phenotypic robustness are moderate. The second plot shows effects of allele combinations; i.e., the epistatic effects on the magnitude of variance. The magnitude of these effects is similar to dominance effects; however, the broad confidence intervals indicate low consistency or power to detect these effects. The lower portion of the second plot furthermore integrates the asymmetric effect of epistasis, delineating whether the effect of allele combination differs between the reciprocal crosses (maternal/paternal effect). The last two plots add the effect of sex of the animals on the effects in the previous two plots. For example, negative inbreeding effect on the variance in females means that the variance tends to be less increased in females of the inbred lines than in males.

Figure 6.

Highest posterior density (HPD) intervals for effects parameters fitted to the Procrustes distance from each specimen to the group mean. Horizontal bars show for each parameter the region of highest posterior density that covers 5 0% (thick line) and 95% (thin line) of the posterior probability. The first panel includes general effects (inbreed overall, strain-specific effects of additive genetics and inbreeding, and maternal effect), the second panel includes effects peculiar to specific strain pairs, the third panel accounts for sex-specific deviations of the general effects, and the fourth panel encompasses sex-specific deviations from the strain pair-specific effects. The “v” and “w” labels in the second and fourth graphs refer to symmetric and asymmetric effects.

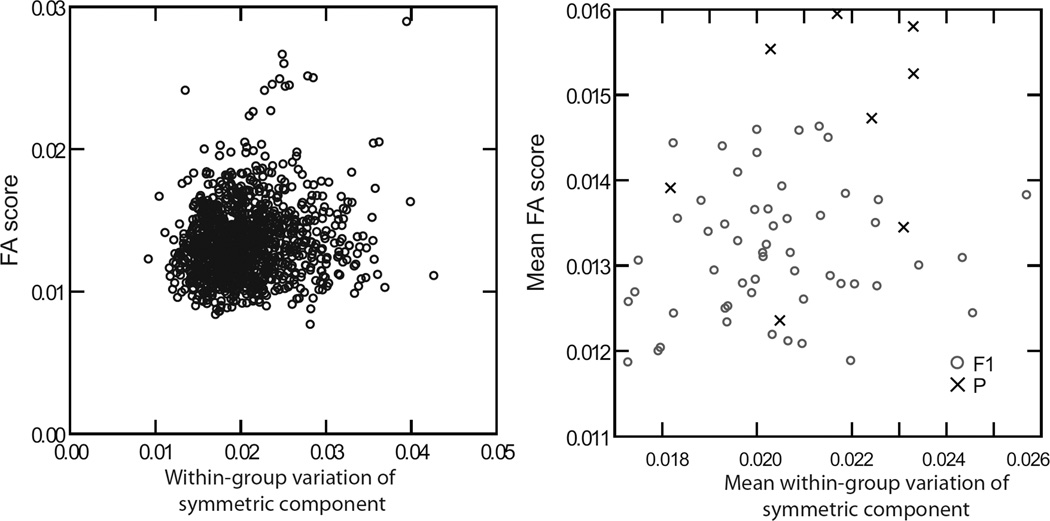
Despite detecting higher phenotypic variation as well as higher fluctuating asymmetry in the inbred lines compared to the heterozygotes, we found no association between the amounts of among-individual phenotypic variation and the degree of FA across the strains, neither when comparing the individual values nor the mean values for each group (Figure 7). Additionally, the averaged distances within groups were not associated with their distances to the grand mean (r= −0.336).

Figure 7.

Scatterplot of the individual values (a) and the group means (b) of the Procrustes distances from each specimen to the group mean and the FA scores.

Discussion

We show that the CC parental strains and their crosses, all of which are isogenic, exhibit variation in both canalization and developmental noise, as measured by within-genotype variation and fluctuating asymmetry. This supports the hypothesis that there is genetic variation among strains in phenotypic robustness. Robustness is thought to be necessary for complex and evolvable developmental systems (Schmalhausen, 1949; Waddington, 1957; Garfield et al., 2013). It is essential for complex systems because it suppresses the effects of mutations or environmental perturbations. Robustness is thought to enhance evolvability because this suppression of mutational and environmental effects can produce “cryptic variation” that is not usually expressed but that can, under the right conditions, become expressed and acted upon by selection (de Visser et al., 2003; Palmer, 2012). Our finding of genetic variation in robustness suggests that there is heritable variation in the extent to which this can occur.

Our results show that FA and among-individual variances are not concordant across strains. The localization of FA and among-individual variation is also different. Cranial regions with higher FA overlap only partially with those displaying larger differences among individuals within each strain. These results suggest etiologic heterogeneity between canalization and developmental stability. Previous studies have reported both lack of concordance between developmental stability and canalization (Debat et al., 2000; Meiklejohn & Hartl, 2002; Takahashi et al., 2010, Breno et al., 2011) as well as significant correlations between these variance components (Clarke, 1998; Willmore et al., 2002; Santos et al., 2005; Breuker et al, 2006; Padró et al., 2014). These inconsistent results may relate to differences among model organisms, phenotypic traits, or sampling strategies. The eight strains analysed here cover 90% of genetic variation found in laboratory mice and three subspecies of Mus musculus. Accordingly, our results suggests strongly that, at least for craniofacial variation, canalization and developmental stability are etiologically distinct.

Our study compares environmental canalization across strains. Environmental conditions are fairly constant across strains, all strains are isogenic, but there is heritable variation in the among-individual variance. Interestingly, a recent study of 19 mouse strains (5 of them corresponding to strains studied here) documented a lack of overlap between QTLs associated with environmental and genetic robustness in gene expression, reinforcing the hypothesis that factors buffering environmental variation do not fully overlap with those buffering genetic variation (Fraser & Schadt, 2010). The diallel design is not well suited to measure genetic canalization as each cross involves the combined effects of entire genomes. Further study of this sample combined with more advanced generations of the Collaborative Cross will allow comparison of the genetic basis for genetic and environmental canalization.

We report a significant positive inbreeding effect for FA and among-individual variance in shape. This supports a relationship between heterozygosity and robustness (Thoday, 1955, 1958; Mather, 1953; Alibert et al., 1994, 1997; Debat et al., 2000). We sought to determine whether this relationship is due to stabilizing selection versus some other benefit of heterozygosity. If stabilizing selection promotes robustness, then robustness should decrease away from the mean, whereas if this does not occur, then stabilizing selection alone cannot influence robustness. Accordingly, we predicted an association between phenotypic extremeness and both among-individual variance and FA among the F1 crosses. All crosses are identical in levels of heterozygosity, but vary in their divergence from overall phenotypic mean. Our results show that neither measure of robustness (FA or among-individual variance) is related to phenotypic extremeness. This result is not consistent with the hypothesis that stabilizing acts on robustness, and provides confirmation for theoretical studies (Hermisson et al., 2003; Hansen et al., 2006; Pavlicev & Wagner, 2012) indicating that stabilizing selection on trait values is unlikely to influence robustness.

The heterosis effect on measurements of developmental stability has previously been documented in laboratory mice with low levels of genetic differentiation (Bader, 1965; Leamy, 1984). However, interbreeding between genetically differentiated lineages can also produce the opposite effect. In this case, hybridization can disrupt epistatic interactions, resulting in increased variance and reduced fitness (Ackermann, 2010). In hybridization among subspecies of mice, the disruption of co-adapted genes increases developmental instability (Auffray et al., 1996; Alibert & Auffray, 2003). This could be the case for the CC mice, since M. m. castaneus and M. m. domesticus are sister subspecies that diverged from M. m. musculus around 435,000–557,000 years ago (Yang et al., 2011; Zheng et al., 2014). Moreover, wild-derived inbred strains have large genetic differences as indicated by a large number of SNPs, structural variants, and indels compared with the reference mouse genome (Keane et al., 2011). However, with the exception of CAST/EiJ, we did not find a consistent decrease of robustness for cranial shape in the crosses between founder groups corresponding to different subspecies (see discussion below). In contrast, mean litter size was lower for crosses involving one or two wild-derived lines in the CC panel, suggesting a reduction in fitness (Philip et al., 2011).

The finding of heritable variation in phenotypic robustness raises the question of the developmental and genetic basis of this variation. One alternative is that particular genes buffer the effects of internal and external perturbations in development (Mitton, 1993; Rutherford, 2000). This view is supported by experiments showing that modulations of HSP90 protein and CyclinG gene activity decrease canalization (Queitsch et al., 2012; Debat & Peronnet, 2013; Rohner et al., 2013) and by reports of QTLs that affect developmental stability of a trait separately from the trait value (Hall et al., 2007). However, other studies have failed to replicate these findings in other systems, which is probably related to a background dependent effect (Milton et al., 2003; Debat et al., 2006, Leamy & Klingenberg, 2005).

The alternative view is that phenotypic robustness is produced by more general properties of developmental architecture (Soulé, 1982; Soulé & Cuzin-Roudy, 1982; Hallgrímsson, 1998; Siegal & Bergman, 2002; Bergman & Siegal, 2003; Proulx & Phillips, 2005). These studies have focused on how aspects of developmental-genetic architecture such as nonlinearities of processes during development (Klingenberg & Nijhout, 1999; Hallgrímsson et al., 2006, 2009; Mitteroecker, 2009), redundancies among pathways (Krakauer & Plotkin), epistatic interactions (Leamy & Klingenberg, 2005), and the averaging effects of multiple independent sources of variation (Soulé & Cuzin-Roudy, 1982; Hallgrímsson, 1998; Hallgrimsson et al., 2002) contribute to canalization and developmental stability. Our results do not definitively distinguish between these two alternative explanations. However, the complex pattern of genetic variation we report for both canalization and developmental stability, combined with the strong heterosis effect is more consistent with this latter view than it is with the former.

Heritability does not equate to evolvability (Hansen et al. 2011) and so the presence of genetic variation for robustness need not imply that it is evolvable. Early selection experiments managed to alter environmental variance in both wildtypes and mutant strains of Drosophila and mice (Dun & Fraser, 1958; Rendel et al., 1966; Rendel, 1967). The results of such experiments have been interpreted to mean the effects of “modifier genes” can be modulated by selection to alter the amount of phenotypic variance expressed in the face of a particular range of environmental or genetic influences (Scharloo, 1991). The extent to which robustness can respond to selection depends on the developmental mechanisms that underlie canalization. If, for instance, canalization occurs not because of epistatic effects but rather as a side-effect of nonlinearities that are deeply embedded in multiple mechanisms, the apparent additive variance for robustness may actually reflect some form of averaging out of disparate non-additive effects. Recent quantitative genetics work has shown that in fluctuating environments, stabilizing selection on epistatic effects can actually reduce canalization (Le Rouzic et al., 2013). Improved understanding of the quantitative genetics of epistasis is critical to explaining how phenotypic robustness evolves (Hansen & Wagner, 2001; Hansen et al., 2006; Hansen 2013).

Developmental stability may evolve by selection against asymmetry (Thornhill & Møller, 1997). The presence of additive genetic variance for FA should allow developmental instability to respond to natural selection on asymmetry (Fuller & Houle, 2003; Carter & Houle, 2011). However, the expected correlation between phenotypic asymmetry and developmental instability is not strong. For a single trait, developmental stability produces a potential variance for both sides, meaning that most individuals with low developmental stability will actually be quite symmetrical. The expected correlation between phenotypic asymmetry and developmental stability increases as the number of independent traits increases. Craniofacial shape is a highly complex trait and it would be difficult to estimate an expected relationship between developmental stability and phenotypic asymmetry. Accordingly, a small amount of additive genetic variance in FA might reflect a larger underlying genetic variance for developmental instability (Fuller & Houle, 2003). Selection may also acts on other consequences of variation in developmental stability rather than directly on morphological asymmetry.

Finally, genetic variation for phenotypic robustness has biomedical implications. Phenotypic heterogeneity is a common feature of structural birth defects where patients often exhibit a range of expression for a specific mutation (Heussler et al., 2002). This may be because of genetic background effects, because of maternal effects on gene regulation (Wolf & Cheverud, 2009), or because the mutation itself influences system-wide robustness in some way (Flatt, 2005). The existence of genetic variation in robustness among the CC founder strains and crosses suggests that genetic backgrounds vary in their degree of buffering to environmental variation. We know that increased variance or fluctuating asymmetry is a common feature of mutations with large phenotypic effects (Soulé & Cuzin-Roudy, 1982; Hallgrímsson et al., 2006, 2009). It is also known that mutations in mice often vary in phenotypic effect depending on the background (Threadgill et al., 1995; Van Bogaert et al., 2006; Rustay et al., 2010; Navarro et al., 2012; Mulvey et al., 2014) and this is also true in other systems (Chandler et al., 2014). Variation in canalization is a largely unexplored explanation for phenotypic heterogeneity in structural birth defects and other genetic diseases.

Conclusions

This paper provides a comprehensive analysis of phenotypic robustness of skull shape in a nearer full diallel panel of the reciprocal crosses between the 8 founder strains of the Collaborative Cross. The breeding design and the methodological approach followed here allowed us to evaluate properties of developmental instability and canalization of complex morphologies that have been controversial. Our central conclusions are: a) there is genetic variation in both components of phenotypic robustness for skull shape among the CC strains, and that a moderate additive effect on these components is detectable; 2) the variances that reflect developmental instability and environmental canalization do not covary among genotypes; 3) heterozygosity has a significant effect in reducing the magnitude of phenotypic variation compared to homozygous parental strains, which is not related to phenotypic extremeness. Mechanisms that determine variation in developmental robustness are relevant to understanding the genetics of complex traits, the variability of expression in human birth defects, and the evolvability of morphology. Our results suggest the need for further work on the quantitative genetics of phenotypic robustness in mice. To yield mechanistic insight, however, such studies must be mirrored by investigation of the developmental basis for variation in robustness. Here, we contribute to the groundwork for such integrated developmental and quantitative genetic studies.