Feature-based attention and spatial selection in frontal eye fields during natural scene search

Feature-based attention helps us to locate objects efficiently during visual search, but how the brain implements FBA in natural scenes remains an open question. We trained macaque monkeys to search for targets in natural scenes while recording from the frontal eye field (FEF). Although the monkeys performed the task well, we found that task-relevant visual features were weak predictors of gaze behavior. Furthermore, we found that task-relevant visual features did not modulate FEF activity.

Abstract

When we search for visual objects, the features of those objects bias our attention across the visual landscape (feature-based attention). The brain uses these top-down cues to select eye movement targets (spatial selection). The frontal eye field (FEF) is a prefrontal brain region implicated in selecting eye movements and is thought to reflect feature-based attention and spatial selection. Here, we study how FEF facilitates attention and selection in complex natural scenes. We ask whether FEF neurons facilitate feature-based attention by representing search-relevant visual features or whether they are primarily involved in selecting eye movement targets in space. We show that search-relevant visual features are weakly predictive of gaze in natural scenes and additionally have no significant influence on FEF activity. Instead, FEF activity appears to primarily correlate with the direction of the upcoming eye movement. Our result demonstrates a concrete need for better models of natural scene search and suggests that FEF activity during natural scene search is explained primarily by spatial selection.

NEW & NOTEWORTHY

Feature-based attention helps us to locate objects efficiently during visual search, but how the brain implements FBA in natural scenes remains an open question. We trained macaque monkeys to search for targets in natural scenes while recording from the frontal eye field (FEF). Although the monkeys performed the task well, we found that task-relevant visual features were weak predictors of gaze behavior. Furthermore, we found that task-relevant visual features did not modulate FEF activity.

a central question in neuroscience is how the brain selects eye movement targets. Eye movements align objects with the high-acuity fovea of the retina, making it possible to gather detailed information about the world. In this way, eye movements inform critical everyday behaviors, including gathering food and avoiding danger. However, from among a torrent of visual stimuli, only some are important for the task at hand. How does the brain prioritize information for eye movement selection?

Prioritizing visual information becomes easier when we search for a target object known in advance. This allows us to use target features such as shape and color to guide our search and filter irrelevant information (Malcolm and Henderson 2009). How exactly the brain performs this computation remains unclear. A leading hypothesis posits that feature-based attention guides the deployment of spatial selection (Wolfe 1994). During fixation, parts of the visual periphery similar to the search target are assigned high priority. We refer to this as feature-based attention. This spatial priority map may then be used to select a part of the visual field to make an eye movement to. We refer to this as spatial selection. In this way, feature-based attention and spatial selection cooperate to influence eye movements.

One brain region thought to be important for selecting eye movements is the frontal eye field (FEF), a prefrontal area on the anterior bank and fundus of the arcuate sulcus (Ferrier 1875; Bruce and Goldberg 1985; Bruce et al. 1985). Extensive literature has highlighted the FEF's role in attention and eye movement planning (Zhou and Desimone 2011; Moore and Fallah 2004; Thompson et al. 2005; Schall 2004; Schafer and Moore 2007; Buschman and Miller 2009). One central finding is that the FEF appears to be selective for both bottom-up saliency (Thompson and Bichot 2005; Schall et al. 1995) and task-relevant visual features (Bichot et al. 1996; Bichot and Schall 1999; Zhou and Desimone 2011). Crucially, distractors that share a greater number of features with the target (e.g., shape, color) lead to higher firing rates. These results implicate the FEF in feature-based attention because they demonstrate selectivity to target-relevant features in FEF independent of eye movement selection.

However, many of these studies have been conducted in artificial settings that lack the richness of a more naturalistic environment. First, typical artificial stimuli contain only a handful of distracting objects, whereas natural scenes contain hundreds or thousands. Second, conventional tasks used to study eye movements require a small number of task-instructed saccades, whereas in the natural world we often make tens of self-guided saccades to explore a scene. Therefore, it is important to ask how FEF's selectivity for bottom-up saliency and task relevance generalizes to tasks in more complicated natural scenes. Recent work by our laboratory has shown that the apparent encoding of bottom-up saliency by the FEF can be explained away by the direction of spatial selection as defined by the upcoming eye movement (Fernandes et al. 2014). This discrepancy in findings between studies using artificial and natural stimuli suggests that the way the brain selects targets for eye movements during natural vision remains an open question.

Here we investigated the role of the FEF in feature-based attention and spatial selection during natural scene search. In particular, we asked if FEF activity is driven by visual features of the search target, by the upcoming eye movement (as a result of spatial selection), or by both. To this end, we recorded from FEF neurons while macaque monkeys searched for known targets embedded in naturalistic stimuli. We then modeled neural activity as a function of target features and the direction of upcoming eye movements. We found that the direction of the upcoming eye movement explained a considerable amount of neural variability, whereas task-relevant visual features did not. Therefore, the reflection of feature-based attention in FEF activity appears to be explained by spatial selection.

METHODS

Animals and Surgery

We used three adult female rhesus monkeys (Macaca mulatta), ages 14–17 yr, and weight 5–6 kg. We refer to them as M14, M15, and M16. Northwestern University's Animal Care and Use Committee approved all procedures for training, surgery, and experiments. Each monkey received preoperative training followed by an aseptic surgery to implant a recording cylinder above the FEF, as well as a titanium receptacle to allow head fixation. Surgical anesthesia was induced with thiopental (5–7 mg/kg iv) or propofol (2–6 mg/kg iv) and maintained using isoflurane (1.0%-2.5%) inhaled through an endotracheal tube. For single electrode recordings performed in M14 and M15, an FEF cylinder was centered over the left hemisphere at stereotaxic coordinates anterior 25 mm and lateral 20 mm. Chronic recording with a recording microdrive was used to record from multiple units in monkeys M15 and M16. The recording chambers for these microdrives were centered and mounted at stereotaxic coordinates anterior 24 mm and lateral 20 mm (M15 left hemisphere; M16 right hemisphere).

Behavioral Tasks

We analyzed data from two different experiments involving visual search in natural scenes: the fly search task and the Gabor search task (Fig. 1). Importantly, both tasks were designed to generate large numbers of purposeful, self-guided saccades. Across all sessions and tasks, monkeys performed ∼300–1,500 trials per session. Thus, for a typical task comprising ∼20 sessions, ∼6,000–30,000 images were shown.

Fig. 1.

Example stimuli used in natural scene search tasks. Targets were blended into the natural scenes and monkeys were given a water reward for finding the target within a fixed number of saccades. For the sake of illustration, targets are encircled in red; the fly is shown unblended since it is difficult to see at this resolution.

To control experimental stimuli and data collection, we used the PC-based REX system (Hays et al. 1982), running under the QNX operating system (QNX Software Systems, Ottawa, ON, Canada). Visual stimuli were generated by a second, independent graphics process (QNX-Photon) and rear-projected onto a tangent screen in front of the monkey by a CRT video projector (Sony VPH-D50, 75-Hz noninterlaced vertical scan rate 1,024 × 768 resolution). The distance between the front of the monkey's eye and the screen was 109 cm (43 in.). Each natural scene spanned 48 × 36° of the monkey's visual field.

Fly search task.

In this task, monkeys (M14 and M15) were trained to locate a picture of a small fly embedded in photographs of natural scenes. Monkeys initiated each trial by fixating a central red dot for 500-1,000 ms, after which the scene and fly target appeared on the screen, and the fixation dot disappeared. The fly target was placed pseudorandomly so that its location was balanced across eight 45° sectors. Within these sectors, the fly target was pseudorandomly placed between 3 and 30° of visual angle from the center of the screen. The trial ended when either the monkey fixated a 2°-window around the target for 300 ms or failed to find the target after 25 saccades. When the target was found and successfully fixated, the monkey was rewarded with water (for details see Fernandes et al. 2014; Phillips and Segraves 2010).

The natural scene images used for this task were drawn from a library of over 500 images, originally used for Phillips and Segraves (2010). Photographs were taken with a digital camera and included scenes with animals, people, plants, or food. Image order was chosen pseudorandomly so that images were repeated only after all others had been shown. Although each unique scene was repeated ∼10 times over the course of the search task, since the locations of the targets were randomized, memorization was not likely to be useful and the monkey had to search visually on each trial to successfully find the target.

Since the monkeys quickly learned to perform the task using only a small number of saccades, we made the task more difficult by blending the fly image with the background photographs. We did this using a standard alpha-blending technique (see Fernandes et al. 2014 for details). Even for targets with a transparency of ∼65%, the average success rate across animals and sessions approached ∼85%.

Gabor search task.

In this task, monkeys (M15 and M16) were trained to locate a Gabor wavelet embedded in photographs of natural scenes. Gabor wavelets are oriented gratings convolved with a local Gaussian and have been used extensively in studies of visual search (Najemnik and Geisler 2005). Here, we used Gabor wavelets because their properties can be easily manipulated (e.g., orientation) and because natural scenes often contain oriented textures. Taken together, this made it possible to quantify “relevant” features in the environment in the sense that image patches sharing features (e.g., orientation) with the Gabor wavelet could be expected to draw the monkey's gaze. In these experiments, we used Gabor wavelets with the same orientation (either vertical or horizontal) within each session. Task parameters and background images were similar to those used in the fly search task. This task was significantly more difficult than the fly search task and both monkeys did not exceed an average success rate of ∼50%.

Data Acquisition and Preliminary Characterizations

Eye tracking.

To track eye gaze behavior, we recorded monkeys' eye position with a precision of up to 0.1° resolution. M14 and M15 received an aseptic surgery to implant a subconjunctival wire-search coil to record eye movements for the fly search task. The coil was sampled at 1 kHz. Eye movements of M15 and M16 were measured using an infra-red eye tracker for the Gabor search tasks (ISCAN, Woburn, MA, http://www.iscaninc.com/), which samples eye position at 60 Hz.

Saccade detection.

We detected saccade onsets and offsets from the kinematics of recorded eye position. We used a threshold of 80°/s for start velocity and marked a saccade starting time when the velocity increased above this threshold. Likewise, saccade-ending times were marked when the velocity fell below 100°/s at the end of this period of decrease. Saccades longer than 80° or with duration longer than 150 ms were discarded as eye-blinks or other artifacts. Fixation locations were computed as the median (x, y) gaze coordinate in the intersaccadic interval.

Neural recording.

We analyzed experiments that used two different electrophysiological recording setups. One set of experiments (the fly search task) used single-electrode recordings, whereas the other sets of experiments (Gabor search tasks) used chronic microdrives to simultaneously record multiple units.

Single-electrode recording.

For monkeys M14 and M15 in the fly search task, single-electrode activity was recorded using tungsten microelectrodes (A-M Systems, Carlsborg, WA). Electrode penetrations were made through stainless steel guide tubes that just pierced the dura. Guide tubes were positioned using a Crist grid system (Crist et al. 1988; Crist Instruments, Hagerstown, MD). Recordings were made using a single electrode advanced by a hydraulic microdrive (Narashige Scientific Instrument Lab, Tokyo, Japan). The interelectrode distance was 1.0 mm. Online spike discrimination and the generation of pulses marking action potentials were accomplished using a multichannel spike acquisition system (Plexon, Dallas, TX). This system isolated a maximum of two neuron waveforms from a single electrode. Pulses marking the time of isolated spikes were transferred to and stored by the REX system. During the experiment, a real-time display generated by the REX system showed the timing of spike pulses in relation to selected behavioral events.

Recordings were confirmed to be in the FEF by the ability to evoke saccades with current intensities of ≤50 μA (Bruce et al. 1985). To stimulate electrically, we generated 70-ms trains of biphasic pulses, negative first, 0.2 ms width per pulse phase, delivered at a frequency of 330 Hz.

Chronic recording.

For monkeys M15 and M16 in the Gabor search tasks, recordings were performed using a 32-channel chronically implanted electrode microdrives (Gray Matter Research, Bozeman, MT). The depth of each individual tungsten electrode (Alpha-Omega, Alpharetta, GA) was independently adjustable over a range of 20 mm. The interelectrode distance was 1.5 mm.

All electrodes were initially lowered to pierce the dura. Individual electrodes were then gradually lowered until a well-isolated unit was located. In general, only a subset of electrodes was moved on any given day, and electrodes were left in place for at least 3 days before further lowering.

Both spikes and local field potentials (LFPs) were recorded with a multichannel acquisition system (Plexon, Dallas, TX) based on a separate PC. Spike waveforms, sampled at 40 kHz were stored for offline sorting. In addition, a continuous analog record of electrode signals sampled at 20 kHz was saved for offline LFP analysis. Automatic spike sorting was performed offline using the Plexon Offline Sorter (Plexon).

Since any given electrode was often left in place for multiple days, we likely recorded from the same neuron across sessions. Therefore, we combined data from units that persisted across recording sessions on different days by manually comparing spike waveforms from units recorded at the same site on different days. Generally, we merged units sharing waveform shape (rise/fall characteristics, concavity/convexity, etc.) and time course. Ambiguous cases were not combined, and waveforms that did not have a single characteristic shape were considered to represent multiunit activity (multiple single units), which were also included for analysis. See Table 1 for the entire set of animals, tasks, and units analyzed.

Table 1.

List of units characterized by cell type and list of modeled units

Animal	Task	Sessions	Characterized Units	V	M	VM	Undetermined	Modeled Units
M14	Fly	19	19	10	1	9	7	15
M15	Fly	27	27	11	3	4	1	25
M15	Gabor (H)	27	93	13	24	56		81
M16	Gabor (H)	36	76	18	21	37	—	57
M16	Gabor (V)	11	49	18	7	24	—	49

The H or V in brackets indicates the orientation of the target for the Gabor search tasks. V, M, and VM are visual, movement, and visuo-movement cell types. We could not determine cell types for a small fraction of the cells in the fly task (undetermined cells). We were able to model the majority of characterized units (modeled units), although certain units needed to be discarded due to low firing rates.

To verify that our recording sites were in the FEF, we used microstimulation to evoke saccades in two of three monkeys (M14 and M16) for both tasks and M15 for the fly search task. For the single-electrode recordings in the fly search task (M14, M15) we stimulated at the end of each recording session and only used data from sessions that reliably evoked saccades with thresholds of ≤50 μA (Bruce et al. 1985). For the implanted electrode microdrives (M16), we only used units isolated from electrodes for which saccades could be evoked with thresholds of ≤50 μA. Since M15 was required for future experiments and stimulation quickly degrades the recording fidelity of the tungsten electrodes, we were unable to stimulate to verify the location of our recording sites for the Gabor search tasks in this monkey. As a result, we were able to verify FEF location with stimulation in only one (M16) of the two chronically implanted monkeys. However, in M15 the chronic microdrive was centered at the stereotaxic location matching maximum FEF evoked saccade sites in M16 and 3 other monkeys used in previous studies. Furthermore, we limited our analyses to units that had properties (receptive field structure and response characteristics) expected in the FEF (see FEF cell characterization below). This decreased the chance of analyzing units from nearby brain regions that were not part of the FEF.

FEF cell characterization.

In the fly search task experiments, cell type characterization was performed for all cells using a standard battery of tests (memory-guided delayed saccade task and visually guided delayed saccade task; for details see Phillips and Segraves 2010; Fernandes et al. 2014). We excluded cells not meeting criteria for having either visual-related activity or movement-related activity. From this dataset, we analyzed 46 neurons (21 visual cells, 4 movement cells, 13 visuomovement cells, and 8 other cells that did not pass any of these criteria; see Table 1).

For the Gabor search task experiments, we did not use the standard battery due to the large number of simultaneously recorded cells resulting from chronic recordings. Instead, we used activity from the natural scene search to estimate the degree of visual and motor activity. In particular, we labeled cells as having visual activity (visual cells) if the firing rate changed significantly from baseline when the natural scene flashed on (baseline interval: 100-0 ms before scene onset; test interval: 5–150 ms after scene onset; Wilcoxon rank-sum test, P < 0.005). Similarly, we labeled cells as having movement activity (movement cells) if the firing rate at saccade initiation exceeded that at baseline in any of 8 (45°) binned directions (baseline interval: 300-200 ms before saccade initiation; test interval: 50 ms before to 50 after saccade; Wilcoxon rank-sum test, P < 0.005). If they passed both tests, we considered them as visuomovement cells. From these datasets, we analyzed a total of 218 cells (49 cells that passed the visual test only, 52 cells that passed the movement test only, and 117 cells that passed both the visual and movement tests; see Table 1).

Behavioral Data Analysis

Relevance map.

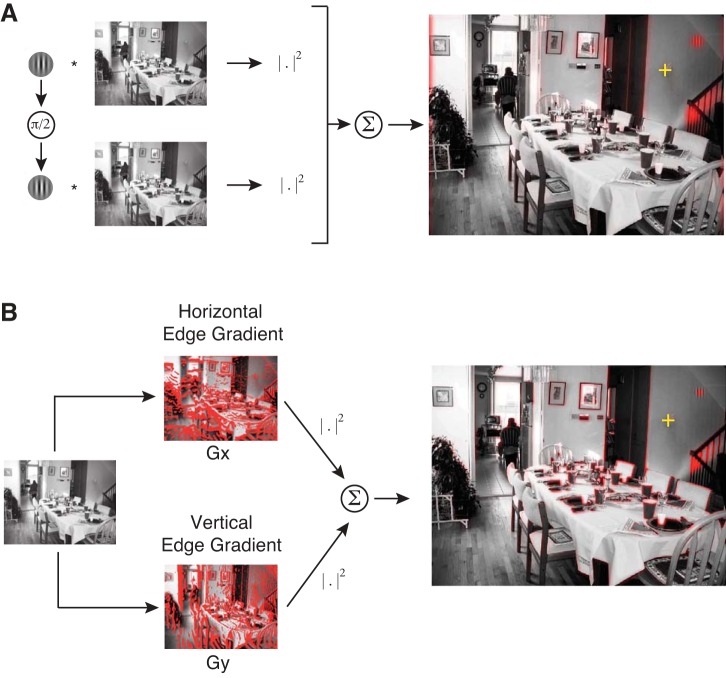
This study asks whether FEF activity reflects feature-based attention as a means to select eye movements. In our visual search tasks, we operationalized feature-based attention as a bias for visual features similar to the search target. We therefore define these target-similar visual features as “relevant” for the search task. To examine whether relevance influences search behavior and FEF activity, we needed to precisely define relevance. We generated relevance “maps” by performing a two-dimensional convolution of the visual scene with the search target. If an image patch is similar to the target, their convolution will yield a large value. In practice, to avoid sensitivity to the precise phase of the Gabor, we convolved the target as well as its 90° phase-shifted version with the scene. We then took the sum of squares of the convolutions (Ramkumar et al. 2015; see Fig. 2A). This operation effectively measures the low-level visual feature overlap between image regions and the search target. Because our search tasks used different search targets (horizontal Gabor wavelet, vertical Gabor wavelet, fly image), we generated relevance maps separately for each task. For the fly search task, which used color images, we summed the relevance map over the three color channels (RGB).

Fig. 2.

Operational definition of relevance (target similarity) and edge energy. A: relevance maps were obtained by convolving the target and its quadrature phase shift with the natural scene and then taking the sum of their squares. B: edge-energy maps were computed by taking the sum of squares of horizontal and vertical edge gradients. Before computing the relevance and energy maps, the image was degraded in accordance with decreasing visual acuity in the periphery, with respect to an example fixation location shown as a yellow crosshair [adapted from Ramkumar et al. 2015].

Edge-energy map.

Edge energy of natural scenes is known to influence the fixation choice of both humans and monkeys in visual search (Ramkumar et al. 2015; Rajashekar et al. 2003; Ganguli et al. 2010). Therefore, we also computed edge energy as a potential feature that may influence fixation choice, defined as the sum of squares of the vertical and horizontal edge gradients (Fig. 2B; for details, see Ramkumar et al. 2015). For the fly search task, we calculated the energy maps for each of the RGB color channels and summed them.

Itti-Koch saliency map.

Although this study emphasizes the effect of feature-based attention (relevance) on behavior and FEF activity, we also analyzed bottom-up saliency, as it has been influential in eye movement behavior and FEF electrophysiology (Fernandes et al. 2014). We operationally defined bottom-up saliency using the Itti-Koch model (Walther and Koch 2006). This model defines saliency in terms of contrast of luminance, color, and orientation at multiple spatial scales.

Analysis of the effect of visual features on fixation selection.

Before examining the electrophysiological data, we asked whether visual features (relevance, energy, and saliency) did indeed guide eye movements in behavior. More specifically, we asked whether the visual features predicted eye movements to those locations. To do this, we performed a receiver operator characteristic (ROC) analysis. To construct the ROC curves, we used the experimentally measured locations of saccade endpoints (fixations), in conjunction with the model-based feature maps (described above) for each image viewed by the monkeys. If feature maps indeed predict fixation locations, saccade endpoints should fall on image patches with higher values of the respective maps than those not drawing saccades.

To control for center bias in our scenes, we used a shuffle control approach. We did this because human-photographed scenes often include interesting objects (those likely to be relevant) in the center of the image (Kanan et al. 2009; Tseng et al. 2009). This makes it possible, for example, to misattribute fixation selection to a certain visual feature when the better explanation is simply that the observer tends to look towards the center of the image/screen. To control for this possibility, we asked whether the predictive power of visual features at fixated patches (for a given image) was greater than that of the features of the same patches (same fixation locations) superimposed on a randomly chosen image. If the predictive power of feature maps was only due to center bias, the visual features at fixated patches in true images should not be more predictive of saccades than the features of image patches in randomly chosen images on average.

Although it is well known that visual acuity is strongest at the fovea and falls off with eccentricity, predictive models of gaze behavior have not taken it into account. Indeed, we have recently shown that modeling visual acuity has enabled the discovery of gaze strategies at different time scales during visual search (Ramkumar et al. 2015). Therefore, to model decreasing visual acuity with peripheral distance, we processed the stimuli before computing the feature maps. More specifically, we applied a peripheral degradation filter with respect to the previous fixation location (see Ramkumar et al. 2015 for details).

To compare the distribution of feature (relevance, edge energy, or salience) values for fixated patches in the true images and shuffled-control images, we generated the feature probability distribution functions (PDFs) by aggregating behavioral data across days for each monkey. We then generated the cumulative distribution function (CDF) of these PDFs for true and shuffled fixation patterns. To compare these two distributions, we plotted the true CDF vs. the shuffled CDF, effectively yielding an ROC curve. We then computed the area under the ROC curve for each behavioral session from the Gabor search tasks.

Neural Data Analysis

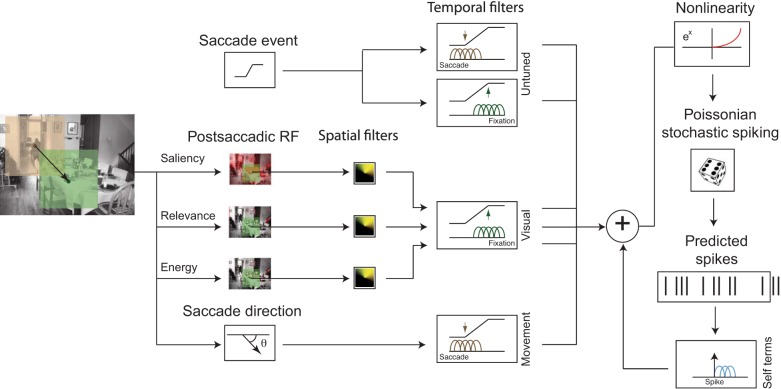
The goal of this study is to ask what factors influence FEF activity during natural scene search. Because there may be multiple such factors, we used a multiple-regression approach: the Poisson generalized linear model (GLM). We modeled neural activity using factors that potentially influence FEF spiking: upcoming saccade direction (as a proxy for saccadic motor command) and visual features (relevance and saliency). To quantify the extent to which each of these factors explains FEF activity, we fit the model to the experimental data.

Generalized linear modeling.

Here we model extracellularly recorded spiking activity in the FEF as a Poisson process with a time-varying firing rate. The spiking activity of most cortical neurons follow Poisson statistics and we specifically verified that this was a reasonable assumption by checking that the variance was equal to the mean spike count over a wide range of spike counts across tasks, animals, and neurons. In general, it is reasonable to assume that the variability around the mean spike count is Poisson distributed for sufficiently narrow time bins within which the neuron's firing rate can be assumed to be constant (homogeneous). We used 10-ms time bins in our models. To model nonnegative, time-varying firing rates, explanatory features are linearly combined and then passed through an exponential nonlinearity (the Poisson inverse link function) (Fig. 3). The number of spikes in each 10-ms time bin is then drawn randomly from a Poisson distribution with the mean given by the estimated firing rate in that bin.

Fig. 3.

Schematic illustration of the comprehensive generative model of neural spikes using a generalized linear model (GLM) framework. The model comprises visual features: saliency, relevance, and energy from a neighborhood around fixation location after the saccade, untuned responses aligned to saccade and fixation onsets, and the direction of the saccade. The features are passed through parameterized spatial filters (representing the receptive field) and temporal filters. The model also comprises spike history terms (or self terms). All these features are linearly combined followed by an exponential nonlinearity, which gives the conditional intensity function of spike rate, given model parameters. Spikes are generated from this model by sampling from a Poisson distribution with mean equal to the conditional intensity function. Brown: basis functions modeling temporal activity around the saccade onset; green: basis functions modeling temporal responses around the fixation onset; blue: basis functions modeling temporal responses after spike onset.

To accurately model FEF neurons, we included the known characteristics of FEF receptive fields (RFs). FEF cells are typically influenced by movement and/or visual features in a particular part of retinocentric space and have a stereotypical temporal response. In particular, firing rates of classical visually tuned neurons are typically modulated by visual features within the RF. Likewise, classical movement-tuned neurons are modulated by upcoming/current eye movements in the direction of the preferred movement direction (movement field). Thus FEF RFs have both spatial and temporal components. We jointly estimated the spatial visual receptive field, the movement receptive field, as well as the temporal response to visual and movement features.

For mathematical tractability, we also assume that the spatial and temporal parts of the RF are multiplicatively separable. Details of the parameterization and fitting process are provided below.

Spatial receptive field parameterization.

Spatially, FEF RFs are retinocentric in nature, with centers ranging from foveal to eccentric (Bruce and Goldberg 1985). This is true for classically defined movement, visual, and visuomovement cells. For both movement and visual features, we parameterize space using polar coordinates (angle and eccentricity). More specifically, we use cosine tuning for the angular coordinate and flat tuning for the eccentric coordinate. We chose flat eccentric tuning for mathematical tractability, but this assumption is realistic for many FEF neurons, which tend to have large RFs (Bruce and Goldberg 1985).

Temporal receptive field parameterization.

Because of the unconstrained nature of visual search, modeling the temporal responses of FEF neurons is complex. To simplify the problem, we chose to model only the neural activity in a fixed temporal window surrounding each eye movement (200 ms both before and after saccade initiation, as well as fixation onset) rather than all neural activity in each trial. This interval is large enough to contain both presaccadic activity and postsaccadic fixation-related activity.

The temporal responses of FEF neurons are heterogeneous, so we allowed for sufficient variability in their shape. To do this, we allowed both saccadic motor activity and visual responses to be explained by a range of temporal scales spanning the 400-ms temporal window. More specifically, we convolved the spatial receptive field features with a temporal basis set, {g_i}, consisting of five fixed-width (w_i = 40 ms) raised cosine functions (Eq. 1) centered at times t_i = {−140, −70, 0, 70, 140} ms with respect to saccade onset (for upcoming eye movement-related activity) or fixation onset (for visual activity). Ultimately, these temporal basis functions allow us to explain a wide range of neural response templates related to both saccades and fixation.

$$g_i=\left(1+\cos \frac{t_i-c_i}{2w_i}\right)/2$$ (1)

Generative model.

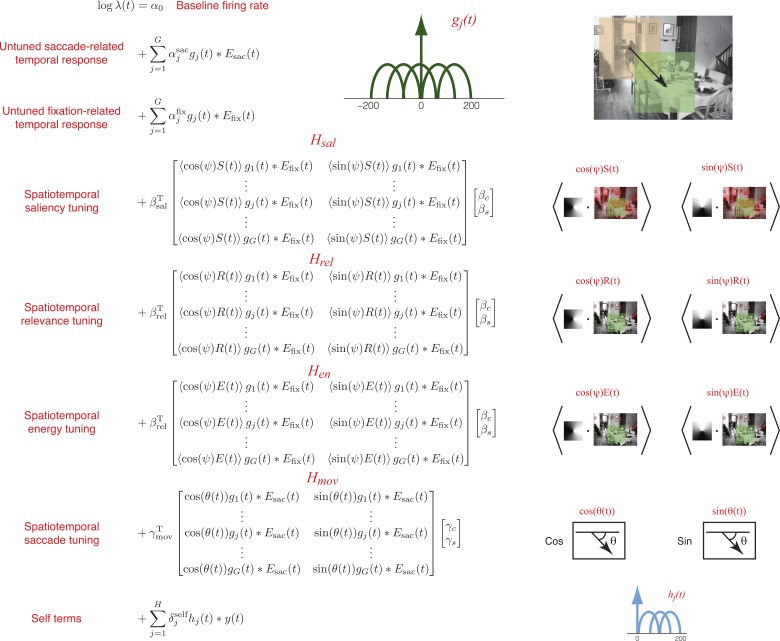
With the use of the above parametric structure, the entire generative model of spike activity is built using the following components (Fig. 4).

Fig. 4.

Parameterization of the generative model. Untuned saccade- and fixation-related temporal responses were modeled using linear combinations of raised-cosine temporal basis functions. Spatiotemporal tuning to saliency, relevance, energy, and saccade direction were modeled using bilinear models with left multipliers representing temporal basis function loadings, and right multipliers representing spatial basis function (cosine and sine) loadings. Additionally, a spike-history (self) term was modeled using a linear combination of temporal basis functions causally aligned to spike events. Parameters of the model were fit using maximum-likelihood with elastic net regularization.

BASELINE FIRING RATE.

We use a scalar term α₀ to model a constant baseline firing rate.

UNTUNED TEMPORAL RESPONSES.

Neurons may have temporal responses to saccade and fixation events that do not depend on direction. We account for this possibility using separate untuned temporal responses aligned to both saccade onset and fixation onset. The untuned saccade-related response is given by ∑_j=1^Gα_j^sacg_j(t) × E_sac(t), where α_j^sac are the free parameters, g_j(t) are the basis functions, and E_sac(t) is an event function (a delta function) specifying saccade onsets. Similarly, the untuned fixation-related response is given by ∑_j=1^Gα_j^fixg_j(t) × E_fix(t). Each untuned response is specified by five free parameters.

SPATIOTEMPORAL VISUAL (SALIENCY, RELEVANCE, AND ENERGY) TUNING.

We modeled the neural activity around a fixation event as a function of the visual features (relevance and saliency) in the RF with respect to that fixation location. For each fixation, we began by extracting the visual features from an image patch (400 × 400 pixels; or ∼13° × 13°) centered on the fixation location. The values for each visual feature were taken from their respective feature maps (see above). To simulate the effect of resolution decreasing with eccentricity, we then applied a blurring transform using image pyramids (Geisler and Perry 1998; see Ramkumar et al. 2015 for details).

We do not know the visual RF a priori; it has to be estimated from the data. To do this, we first constructed the x and y components for each visual feature by applying a spatial cosine and sine mask, respectively, to the visual feature maps of the extracted image patch (Fig. 4). The RF center (preferred angle, Ψ*) can then be inferred from the data by fitting the corresponding weights for the sine and cosine masked images and using the trigonometric identity:

$$\cos \left(\mathrm{\psi }-{\mathrm{\psi }}^{*}\right)=\cos \hspace{0.17em}{\mathrm{\psi }}^{*}\cos \hspace{0.17em}\mathrm{\psi }+\sin {\hspace{0.17em}\mathrm{\psi }}^{*}\sin \hspace{0.17em}\mathrm{\psi },\text{and}$$ (2)

$${\hspace{0.17em}\mathrm{\psi }}^{*}={\text{tan}}^{-1}\left(\frac{\sin \hspace{0.17em}{\mathrm{\psi }}^{*}}{\cos \hspace{0.17em}{\mathrm{\psi }}^{*}}\right)$$

where cosΨ* and sineΨ* are linear model parameters of the GLM.

Along with estimating a spatial RF (via the above parametrization), we also wanted to model the temporal response around the fixation event. To this end, we convolved each spatial covariate (sine and cosine) with each of the five allowed raised-cosine temporal basis functions. Combining all of these parts, the complete spatiotemporal visual response can be succinctly specified by two bilinear models as:

$${\beta }_{\text{sal}}^T{H}_{\text{sal}}\left[\begin{array}{c}{\beta }_{\text{C}}\\ {\beta }_{\text{S}}\end{array}\right]+{\beta }_{\text{rel}}^T{H}_{\text{rel}}\left[\begin{array}{c}{\beta }_{\text{C}}\\ {\beta }_{\text{S}}\end{array}\right]+{\beta }_{\text{en}}^T{H}_{\text{en}}\left[\begin{array}{c}{\beta }_{\text{C}}\\ {\beta }_{\text{S}}\end{array}\right]$$ (3)

where β_sal, β_rel, and β_en are free parameters specifying the temporal response to saliency, relevance, and energy, β_C and β_S specify the angular position of the visual RF; and H_sal, H_rel, and H_en are matrices representing spatial sine and cosine covariates convolved with the temporal basis functions (Fig. 4). Note that we assume the same spatial RF for both saliency and relevance. (i.e., β_C and β_S are the same for saliency, relevance, and energy). Thus we have 5 free parameters each for the saliency, relevance, and energy temporal response, and 2 free parameters for the spatial RF, resulting in a total of 17 free parameters.

SPATIOTEMPORAL SACCADE TUNING.

We modeled the neural activity around a saccade event as a function of the upcoming saccade direction (upcoming “saccadic motor command”). To do this, we constructed the movement covariates as the sine and cosine projections of the upcoming eye movement direction. Note that we do not incorporate previous knowledge of the neuron's RF from RF mapping tasks. As with the visual RF estimation, the angular position of the neuron's movement field can be inferred from the data by fitting the model parameters corresponding to sine and cosine covariates.

As with the visual response, to simultaneously estimate a temporal movement response along with the movement field, we can specify a bilinear model as:

$${\gamma }_{\text{mov}}^T{H}_{\text{mov}}\left[\begin{array}{c}{\gamma }_{\text{C}}\\ {\gamma }_{\text{S}}\end{array}\right]$$ (4)

Altogether, this response is specified by five temporal and two spatial parameters, resulting in seven free parameters.

SPIKE HISTORY TERMS.

To further explain variability in neural activity, we included a spike history term. This feature is not central to the logic of our argument, but serves to improve our model of neural activity. To model the effect of spike history, we simply convolve the spike train with three raised-cosine temporal basis functions, h_j(t) spanning a range of [0 200] ms with respect to each spike event. The basis functions were centered at 60, 100, and 140 ms.

The temporal response for the spike history term is not coupled to any external events (i.e., fixation or saccade onset), and is given by ∑_j=1^Hδ_j^selfh_j(t) × y(t), where y(t) is the spike train that we are modeling with the GLM. This response is specified by three free parameters, δ_j^self, j = 1 2, 3.

Spatiotemporal RF fitting algorithm.

To summarize our model parameterization: we model space with polar coordinates but dispense with eccentricity for mathematical tractability. We model time using raised-cosine temporal basis functions.

For the spatiotemporal model terms, each model feature (saliency, relevance, energy, and upcoming movement direction) is initially parameterized by two covariates: the sine and cosine projections of that feature. We then model temporal responses of each spatial feature with five raised cosine functions. Thus the sine and cosine projection of each spatial feature is convolved with five temporal basis functions. This leads to a total of 40 covariates for the model of saccadic motor and visual activity (4 × 2 × 5 = 40, four features, two spatial coordinates for each feature, five temporal basis functions for each spatial covariate).

For the temporal model terms, the untuned temporal responses aligned to saccade and fixation onsets have five covariates each, and the spike history term provide three covariates. Including the baseline term with all of these gives us a total of 53 covariates.

Using all 53 convolved covariates as an independent variable would make the maximum-likelihood estimation problem linear and convex but could lead to different temporal responses for the sine and cosine terms, making the estimate hard to interpret. For example, it would be difficult to rationalize differing time courses for horizontal and vertical saccades.

To keep the model interpretable, we adopted the bilinear formulations of the spatiotemporal terms given in Eqs. 3 and 4, resulting in a total of 37 (17 for saliency, relevance, and energy, 7 for movement, 10 for untuned, and 3 for spike history terms) free parameters. However, since the log-likelihood of this bilinear formulation is no longer convex, estimating it could result in local minima and would in general suffer from the difficulties of optimizing nonconvex functions.

Therefore, to estimate the parameters of this model, we adopted an iterative algorithm in which we alternatively held the spatial parameters (β_C, β_S, γ_C, γ_S) or the temporal parameters (β_sal, β_rel, β_en, γ_mov) fixed while fitting all the others. In this approach, each iteration step is a convex optimization problem. This method guarantees that the temporal response of each spatial covariate will be the same. We alternated between fitting stages until the model parameters converged.

Model fitting.

We trained and tested our model using nonoverlapping twofold cross validation. To avoid overfitting, we estimated model parameters using elastic net regularization (Hastie et al. 2009; Qian et al. 2013; Friedman et al. 2010) (Glmnet implemented in Matlab). Regularization helps to select for simpler models by penalizing models with large or many parameter values. Elastic net regularization includes two free parameters: α, which determines the strength of L1 relative to L2 penalization, and λ, which determines the strength of regularization. We selected the values of these parameters (α = 0.01, λ = 0.05) on a different data set using cross validation.

Model comparison.

The main goal of modeling spike trains using GLMs was to determine whether FEF activity significantly encodes visual or movement features. To address the main scientific question of whether the FEF encodes task relevant visual features, we fit partial models to the data using relevance covariates only or movement covariates only, and compared them against joint models comprising both relevance and movement covariates. To maximally explain variance and address possible confounding factors, we also fit a more comprehensive and more complex model including saliency, energy and spike history terms. The partial models fell into two categories: leave-out models, and leave-in models. Leave-out models leave out the main feature of interest; the idea is that by comparing a leave-out model against a full model, we can quantify the marginal predictive power of the left out feature. Leave-in models only include the features of interest; the idea is to characterize the apparent encoding of these features by neural activity when other features are not considered. We used leave-out models to assess statistical significance and leave-in models as an interpretive tool for apparent encoding.

To measure the quality of our model fits, we used two metrics: pseudo-R², and conventional-R². Pseudo-R² is related to the likelihood ratio and extends the idea of linear R² to non-Gaussian target variables. The idea of the pseudo-R² metric is to map the likelihood ratio into a [0, 1] range, thus offering an intuition similar to the conventional R² used with normally distributed data. Many definitions exist for the pseudo-R², but we used McFadden's formula (McFadden 1974).

$$R_{\mathrm{D}}{{\displaystyle }}^2\left(\text{model}\right)=1-\frac{\log L\left(\mathrm{n}\right)-\log L\left(\stackrel{}{\hat{\lambda }}\right)}{\log L\left(n\right)-\log L\left(\overline{n}\right)}$$

where logL(n) is the log likelihood of a perfect model, logL$\left(\widehat{\lambda }\right)$ is the log likelihood of the model in question, and logL(n̄) is the log likelihood of a model using only the average firing rate. More specifically, it can be interpreted as the relative improvement that a given model offers above and beyond the simplest possible model (constant firing rate).

We also use a variant of pseudo-R², relative pseudo-R², to compare nested models (e.g., a partial model with the full model). The relative pseudo-R² quantifies the increase in model likelihood as a result of adding back the left-out features from the partial model (also maps to the [0, 1] range). A relative pseudo-R² significantly greater than zero indicates that the left-out feature is a statistically significant explanatory feature.

$$R_D{{\displaystyle }}^2\left(\mathit{\text{model 1, model 2}}\right)=1-\frac{\log L\left(n\right)-\log L\left({\stackrel{}{\hat{\lambda }}}_2\right)}{\log L\left(n\right)-\log L\left({\hat{\lambda }}_1\right)}$$

where logL$\left({\hat{\lambda }}_2\right)$ is the log likelihood of the full model, and logL$\left({\hat{\lambda }}_1\right)$ is the log likelihood of the nested, partial model. It can be interpreted as the relative improvement due to the model components left out by model 1.

We computed pseudo-R² for all models and relative pseudo-R² for all partial models on test sets of both cross-validation folds. We obtained 95% confidence intervals on these metrics using bootstrapping. A left-out feature was deemed significant at four-sigma (P < 0.006; uncorrected for multiple comparisons) if the minimum of the lower bounds of the relative pseudo-R²s was greater than zero (a conservative measure).

Pseudo-R² values are not directly comparable to (are much smaller than) conventional R² and are thus more difficult to interpret. We also computed conventional R² values by calculating the correlation coefficient between 1) the saccade- and fixation-averaged perisaccade time histograms (PSTHs) and 2) the saccade- and fixation-averaged model predictions. Averaging across hundreds of fixations renders Poisson spiking into a smooth curve, which can be compared with the smooth firing rate predictions of the model.

Explaining away.

By using a multivariate modeling approach, we are able to compare the relative contributions of different model components (e.g., visual features and upcoming eye movements). In this section, we elaborate on the nuances of interpreting the results of a multivariate analysis.

Even if two model components are both individually correlated with neural activity, multiple situations related to marginal explanatory power can arise in theory:

If two components explain the “same” neural variability, then they will have overlapping explanatory power. In this case, a multivariate model with both components is unlikely to be significantly better than the single best univariate model.

If two components explain “different” neural variability, then they will have nonoverlapping explanatory power. In this case, a multivariate model with both components is likely to be significantly better than both univariate models.

If two components explain neural variability that is similar but is neither completely identical nor distinct, then an intermediate situation arises. In this case, a multivariate model is likely to be significantly better than both univariate models as the overlap between the two decreases.

Perisaccade time histograms analysis.

In addition to modeling individual neurons using GLMs, we also analyzed them in a conventional way using perisaccade time histograms (PSTHs). We chose to perform this analysis for one set of sessions for which relevance and energy were maximally predictive of fixation choice (i.e., for animal M16, vertical Gabor search task). We computed these PSTHs for two different sets of saccades as follows.

First, we selectively analyzed saccades into the movement RF as follows. We categorized each saccade into one of eight directional bins with bin centers at 0, π/4, π/2, 3π/4, −3π/4, −π/2, and −π/4, and averaged the firing rates in 10-ms time bins across saccades, separately within each directional bin. We then considered the movement-field (movement RF) to be along the directional bin having highest peak firing rate around the saccade. We took this within-RF PSTH for each neuron and max-normalized it, i.e., set the peak firing rate within this bin to 1. We then averaged these normalized PSTHs across neurons to produce a population-averaged PSTH. We separately calculated such a population-averaged PSTH for saccades categorized according to high and low relevance (top 50% of saccades to high- and low-relevance locations) at saccade landings, as well as high and low edge energy.

Second, we selectively analyzed saccades out of the movement RF as follows. As before, we categorized saccades into one of eight directional bins and computed the PSTHs for each directional bin within 10-ms time bins. We then defined saccades out of the RF to be those that were not into the directional bin defined by the maximum peak firing rate (i.e., the movement RF) as well as the two neighboring directional bins. We averaged the PSTHs across these five out-of-RF directional bins. As before, we max-normalized the traces before averaging them across neurons. Crucially, we calculated these out-of-RF PSTHs separately for high and low relevance (top and bottom 50% of saccades) within the presaccadic RFs (not those at saccade landings). We also calculated these PSTHs separately for high and low edge energy, again within presaccadic RFs, not saccade landings.

Power analysis.

Since we found that relevant visual features did not explain FEF activity, we wanted to ask whether our approach had sufficient power to detect such an effect. To do this, we simulated neural data with known parameters (e.g., a weak relevance representation) and attempted to detect the effects of those parameters. We used behavioral data from a single experimental session (eye movements and image features) and simulated spiking activity according to our Poisson model.

To ask whether we could detect a weak effect of relevance, we first simulated neural activity with a range of representation strengths for relevance. As a measure of representation strength, we defined modulation depth as the relative change in firing rate due to a 1 SD change in the given feature. For example, if a fixated image patch had a relevance value that was 1 SD above average, and led to a 10% increase in firing rate from baseline, we would say the modulation depth was 10% (alternatively, 1.1). We explored 10 modulation depths that were evenly spaced between 1.05 and 1.30. We used a baseline firing rate of 20 spikes/s and ensured that average firing rates were the same across modulation depths. To do this, we randomly removed spikes to achieve an average of 20 spikes/s in each condition. A given representation was said to be detectable if the marginal predictive power of relevance was statistically greater than zero (if its 95% confidence interval did not overlap zero).

To explore the consequences of using noisy or inaccurate relevance models, we performed two additional analyses. In the first, we simulated neural data according to our relevance model as above. We then corrupted the relevance model covariates with Gaussian noise before fitting the model.

$$x_{\text{fitted}}=x_{\text{simulated}}+\alpha N$$

where x_simulated is the covariate used for data simulation with μ = 1, σ = 1, x_fitted is the covariate used for fitting, N is Gaussian noise with μ = 1, σ = 1, and α tunes the degree of noise added. In addition to the uncorrupted covariates, we used three levels of noise. These corrupted model covariates used for fitting were correlated with the model covariates used for simulation with r = 0.8, 0.5, 0.2. This procedure allowed us to explore when the effect of relevance was detectable, even if the definition of relevance used for fitting was a noisy version of the “correct” definition.

In the second analysis, we characterized the consequences of simulating and fitting the model with qualitatively different definitions of relevance. Specifically, we simulated the data using edge energy, a visual feature that is correlated with relevance (r = 0.61) and fit the model using relevance (Ramkumar et al. 2015). This allowed us to characterize the effects of fitting the model with an inaccurate version of the “correct” definition of relevance.

RESULTS

When we search for a known target, we can use properties of that target to guide our search. In this study, we ask whether the FEF, a region heavily implicated in eye movement selection, facilitates feature-based attention by biasing gaze towards target features, or whether it reflects spatial selection of subsequent eye movement targets. We recorded a heterogeneous population of FEF neurons from three macaques while they performed several variations of a natural scene search task. In each task, a target known to the monkeys ahead of time was embedded in natural scenes, and the monkeys were rewarded for successfully fixating this target (see methods for details). Since the spatial distribution of targets in the scene was extremely broad and there was no contextual information about their location in the scene, spatial attention would not help them find the target. Furthermore, since the targets are blended into the scene, they do not stand out with respect to their local background. Thus looking for salient objects was not a viable strategy either. However, because the targets were known ahead of time, the monkeys could use target features, task-relevant features, to guide their search. To disentangle possible influences of feature-based attention and spatial selection on FEF activity, we then analyzed the data with a multiple-regression approach.

First, we found that monkeys were able to perform the tasks to varying levels of success (see Table 2 for the search performance of individual monkeys averaged across sessions). The fly task was relatively easier because it was a large, mostly black and white target blended into a colored natural scene and because its position was restricted to a 3–30° range around the center. By comparison, the Gabor task with a grayscale background and a grayscale target uniformly distributed around the scene was significantly harder.

Table 2.

Statistics of search behavior for each monkey and task summarized across sessions

Animal	Task	Trial Duration, s	Success Rate, %	No. Saccades to Locate Target	Fixation Duration in Successful Trials, ms	Fixation Duration in Failed Trials, ms
M14	Fly	1.4 ± 0.3	72.8 ± 7.5	4.7 ± 0.3	185 ± 17	221 ± 47
M15	Fly	1.4 ± 0.4	98.8 ± 6.0	3.3 ± 0.6	302 ± 38	465 ± 317
M15	Gabor (H)	6.1 ± 0.7	49.0 ± 13.1	5.1 ± 0.7	351 ± 45	321 ± 81
M16	Gabor (H)	7.8 ± 1.1	38.8 ± 15.8	7.2 ± 0.9	297 ± 19	303 ± 34
M16	Gabor (V)	6.1 ± 1.2	75.2 ± 19.0	5.4 ± 0.8	316 ± 11	275 ± 49

Values are mean ± SE. The trial duration is the entire duration from scene onset to scene offset. The success rate is the percentage of trials in which the monkey successfully located the target. The number of saccades to find the target is given only for successful trials and includes the last, target-finding saccade. The fixation duration is averaged across all saccades in successful and failed trials.

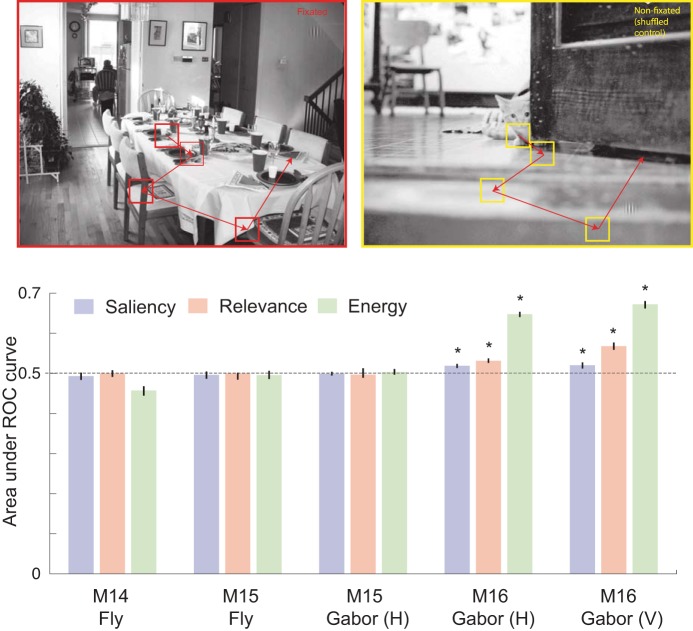
Next, we asked if monkeys indeed use visual features to guide their search. To do this, we performed ROC analysis to examine whether image patches with higher task relevance predicted fixations. Since human-photographed natural scenes are known to have a center bias, we compared the feature distribution of fixated image patches to the feature distribution of the same fixation pattern superimposed on a randomly chosen image (see methods for details). None of the visual features were able to predict fixation choice significantly above chance [area under the curve (AUC) of 0.5] for the fly search task (Fig. 5). For the Gabor task, both relevance and energy predicted fixations only for monkey M16 (Fig. 5). The overall predictive power of relevance was weak (AUC < 0.55) but energy was more strongly predictive of fixations than relevance for the same subset of tasks (Fig. 5; AUC > 0.6). Although the effect size of relevance appears modest, it is reasonable in the context of most predictive models of gaze behavior (for a recent survey, see Borji et al. 2013; the best performing models have an AUC of under 0.6). Thus, at the very least, correlates of task relevance and energy may be encoded by brain regions responsible for saccade selection.

Fig. 5.

Prediction of gaze using visual features at fixation. We compared bottom-up IK-saliency, top-down relevance, and energy at fixated (top left) and nonfixated, i.e., shuffled control (top right) targets by computing the area under the receiver operator characteristic (ROC) curves (bottom). *Statistically significant difference from a chance level of 0.5 at a significance level of P < 0.05.

The ROC analysis only provides us with a session-by-session summary statistic of the influence of search-target related features on fixation selection. To ask if the influence of these features on fixation choice was modulated by search performance, we performed three different analyses.

First, we separately analyzed the fixations from successful and unsuccessful trials. However, we found no significant differences between the AUCs across these two types of trials (not shown). We did not analyze the fly search task in this way because we did not have a sufficient number of failed trials for reliable estimation of ROC curves.

Second, we asked whether the predictive power of visual features (AUC) in a given session was correlated with search performance (percentage of trials in which the monkey found the target). We found a strong correlation between relevance and search performance but only for the vertical Gabor search task performed by M16, for which relevance was significantly predictive of fixation choice (Table 3). Surprisingly, we did not find such a correlation between energy and search performance even though energy was predictive of fixation choice (Table 3). This strongly suggests that whenever relevance has an effect on fixation choice, it also has an effect on search performance. Unlike relevance, energy predicts fixations but not search performance. Thus, although energy is predictive of saccade targets, it may be a bottom-up feature and therefore not an important factor in feature-based attention.

Table 3.

Correlation between success rate and ROC values across sessions

Animal	Task	Relevance vs. Success Rate	Energy vs. Success Rate
M14	Fly	−0.18 (0.52)	−0.49 (0.06)
M15	Fly	r = 0.21, P = 0.31	r = 0.32, P = 0.11
M15	Gabor (H)	r = 0.14, P = 0.49	r = −0.02, P = 0.90
M16	Gabor (H)	r = 0.20, P = 0.25	r = 0.21, P = 0.22
M16	Gabor (V)	r = 0.96, P < 0.0001	r = 0.18, P = 0.60

ROC, receiver operating characteristics.

Third, the natural distribution of saccade velocities is likely to reflect the distribution of urgency with which the animal selects fixations. If the peak velocities of saccades were correlated with relevance or energy, it would suggest that these features influence the conscious choice of fixations. However, we did not find any correlation between peak saccade velocity and relevance or energy (on average across sessions and animals, these correlations did not exceed 0.05; −0.05 ≤ Pearson's r ≤ 0.05).

Taken together, these behavioral analyses suggest that saliency is not predictive, relevance is weakly but significantly predictive, and energy is strongly predictive of fixation locations for a subset of animals and tasks. There appears to be no correlation between behavioral parameters such as peak saccadic velocity and visual features of saccade landings. Importantly, even though relevance was weakly predictive, when it was predictive of saccade choice, its predictive power was correlated with success rate of search behavior.

Based on the weak behavioral effect alone, it is still very possible that the FEF could represent feature-based attention as operationally defined by relevance. Indeed, cortical area V1 represents information such as visual contrast regardless of whether such information directly informs behavioral choices. Although prefrontal regions often relate to behavior (Miller et al. 1996), it is possible that the FEF represents relevance to consider and reject potential saccades to locations that are similar to the target but not sufficiently similar as to warrant a saccade. In such a circumstance, feature-based attention would inform saccadic decisions but would not manifest in measurable fixation behavior, since saccades would only be made to locations that have a very high target similarity. Therefore, it is important to examine neural activity no matter the result of the behavioral analysis.

Next, we asked which features best explain FEF activity during natural scene search. We used a multiple-regression approach to model neural activity while monkeys performed a target search task in natural scenes. More specifically, we used the Poisson GLM framework to explain spiking events in terms of behavior and task variables. We modeled spiking in terms of visual feature maps of relevance and energy, in addition to other features thought to be encoded by the FEF: upcoming eye movements (as a proxy for spatial selection or planning), and visual feature maps of saliency. In this way, we tested the potential influence of feature-based attention on FEF activity during natural scene search.

We found that some neurons appeared to be well explained by a simple model of saccadic motor activity aligned to saccade onsets, based on the direction of upcoming movement alone (Fig. 6). Others initially appeared to be explained by a simple model of relevant visual features alone, aligned to the onset of fixation (Fig. 7).

Fig. 6.

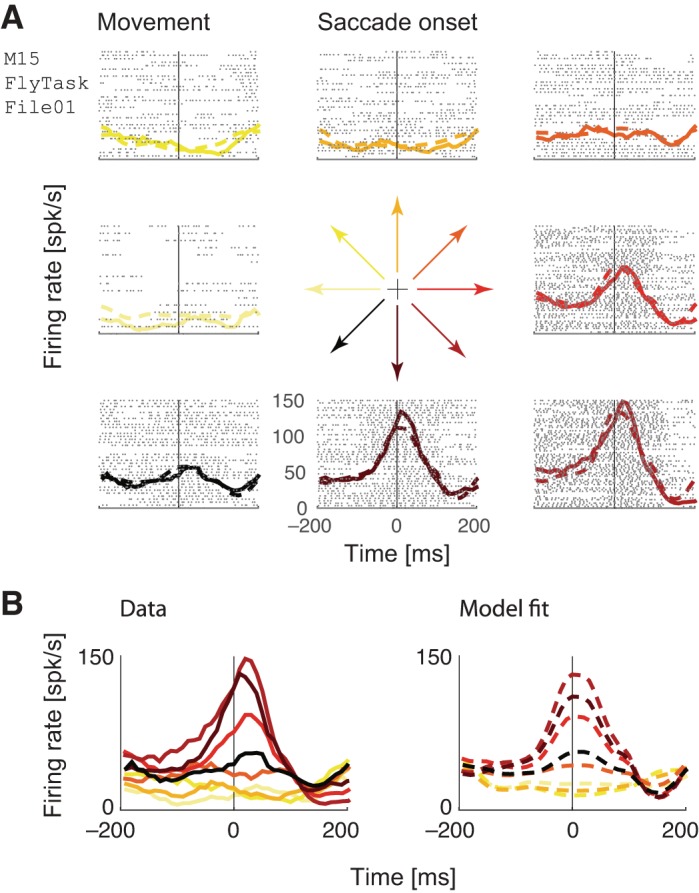
Example neuron fit using a movement-only model. The model was fit to an independent held-out half of the data that is not visualized here. A: raster plots, perisaccadic time histograms (PSTHs) and model predictions, separated into 8 categories according to the direction of the upcoming saccade (color-coded in the central glyph), and aligned to saccade onset (vertical line). B: data and model PSTHs aligned to the saccade onset show tuning to upcoming movement direction.

Fig. 7.

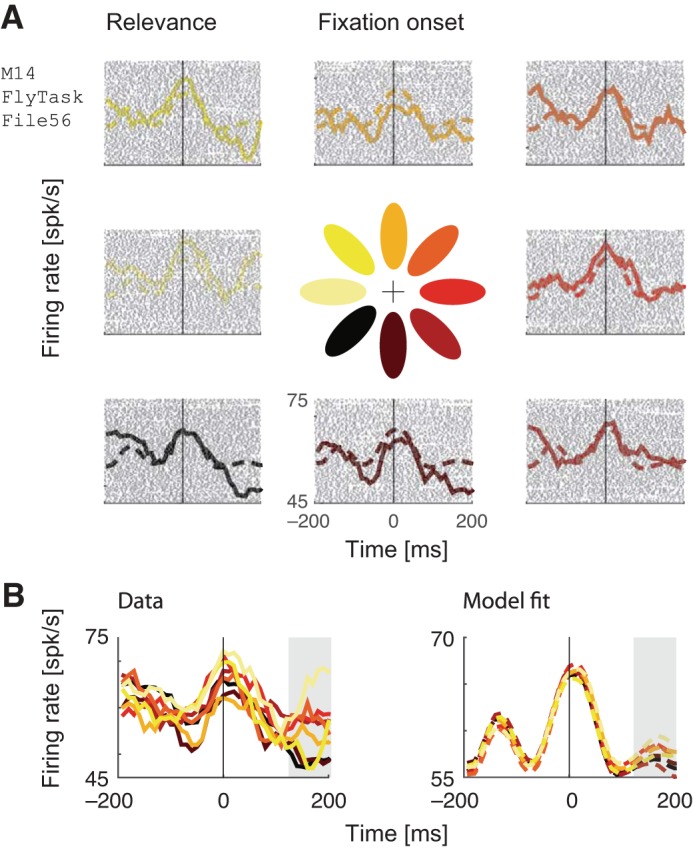
Example neuron fit using a relevance-only model. The model was fit to an independent held-out half of the data that is not visualized here. A: raster plots, fixation-aligned PSTHs, and model predictions, separated into 8 categories according to the direction of the maximally relevant octant (color-coded in the central glyph). B: data and model PSTHs aligned to the fixation onset do not show a clear tuning to direction of maximum relevance during the fixation onset, but do show a modest tuning at ∼200 ms after fixation, as indicated by the gray panel.

Much previous work has characterized the activity of FEF cells as movement-related or visually related using simple, artificial stimuli, and tasks. Therefore, having first established that univariate models can explain both visually related and movement-related activity, we used our multiple-regression approach to characterize neurons in the same way: to what extent is the activity of FEF neurons predicted by upcoming movement, relevance, or some combination thereof? We addressed this question by comparing univariate models of relevance against multivariate models of relevance and movement tuning. We found that although some neurons initially appeared to encode relevant visual stimuli, an upcoming movement was a better predictor of neural activity aligned to fixation (example neuron in Fig. 8A). For most neurons, we found that a relevance-only model was significantly improved by adding a movement covariate (Fig. 8B, top), but a movement-only model was not significantly improved by adding a relevance covariate (Fig. 8B, bottom).

Fig. 8.

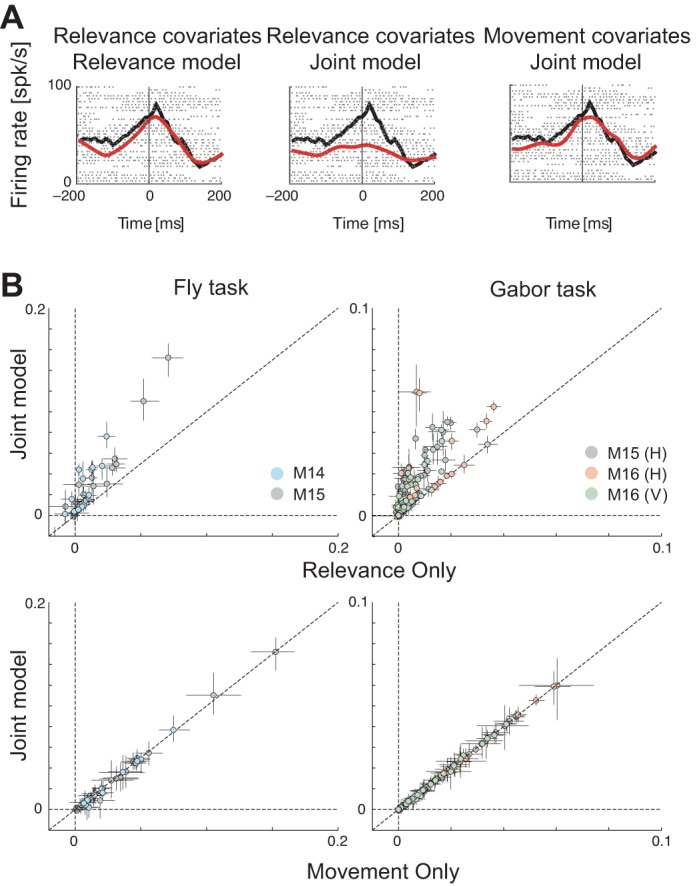
Apparent tuning to relevance is explained away. A: data PSTHs (black) and corresponding model predictions (red) for a single example neuron, of (from left to right): relevance-only model, relevance covariates of the joint model comprising relevance and movement, and movement covariates of the joint model, overlaid on top of each other. Dots show spike rasters. Both rasters and model predictions are aligned to fixation onset. B: scatter plots of pseudo-R² (goodness of fit) values of univariate against multivariate models. Top: relevance-only model vs. a joint model comprising relevance and movement. Bottom: movement-only model vs. a joint model comprising movement and relevance.

We formally quantified the predictive power of relevance and movement using a relative pseudo-R² analysis, which compares a model leaving out the covariate of interest (either relevance or movement) against a joint model comprising both relevance and movement, as well as a full model comprising additional covariates including bottom-up saliency, edge energy, and self terms (see methods). We found that apparent tuning to relevance (Table 4, #1) was progressively explained away when compared against the joint model and the more comprehensive full model (Table 4, #3 and #4). A nearly identical effect was observed for edge energy (Table 4, #5 and #6). However, movement does not get explained away when comparing a model that left movement out against the joint model comprising relevance and movement (Table 4, #2). Therefore, neural activity is correlated with both saccades and relevant image patches, even though only one of the features (upcoming saccades) is truly encoded by neural activity.

Table 4.

GLM analysis summary statistics

Animal	Task	#1 (Rel-Only Model/Rel Neurons)	#2 (Mvt + Rel Model/Mvt Neurons)	#3 (Mvt + Rel Model/Rel Neurons)	#4 (Full Model/Rel Neurons)	#5 (Energy-Only Model/Energy Neurons)	#6 (Full Model/Energy Neurons)
M14	Fly (15)	5	9	0	0	4	0
M15	Fly (25)	8	8	1	0	8	0
M15	Gabor (H) (81)	57	55	1	1	54	1
M16	Gabor (H) (57)	24	25	1	0	28	3
M16	Gabor (V) (49)	23	24	1	0	22	1

Number of neurons that were significantly modulated by relevance, energy, or movement in different models. Neurons were deemed to be significantly tuned if the 4σ confidence intervals of the (relative) pseudo-R²s exceeded zero. We used a strict 4σ threshold to sufficiently correct for multiple comparisons across neurons and models. #1: number of significant neurons for the relevance-only model. #2: number of neurons significantly tuned for movement by comparing a leave-movement-out model against a joint model with movement and relevance. #3: number of neurons significantly tuned for relevance by comparing a leave-relevance-out model against a joint model with movement and relevance. #4: number of neurons significantly tuned for relevance by comparing a leave-relevance-out model against a comprehensive full model (see text). #5: number of significant neurons for the energy-only model. #6: number of neurons significantly tuned for energy by comparing a leave-energy-out model against a comprehensive full model (see text). GLM, generalized linear model.

Although the GLM analysis convincingly suggests that movement explains away any apparent effect of relevance or energy, it may be limited by the specific assumptions of the linear-nonlinear Poisson model. Therefore, we analyzed the data using a more conventional technique by visualizing PSTHs, only for the set of sessions for which relevance and edge energy were maximally predictive of fixation choice (M16, vertical Gabor search). Specifically, we computed population-averaged normalized PSTHs for saccades into the RF (see methods), separated by the top and bottom 50% of relevance (or energy) of saccade landings (Fig. 9, top). We also computed these PSTHs for saccades out of the RF (see methods), separated by the top and bottom 50% of relevance (or energy) in the presaccadic RF (Fig. 9, bottom). We found no significant firing rate differences between these saccades, suggesting yet again that relevance and energy have no aggregate effect on population FEF firing rates during natural scene search.

Fig. 9.

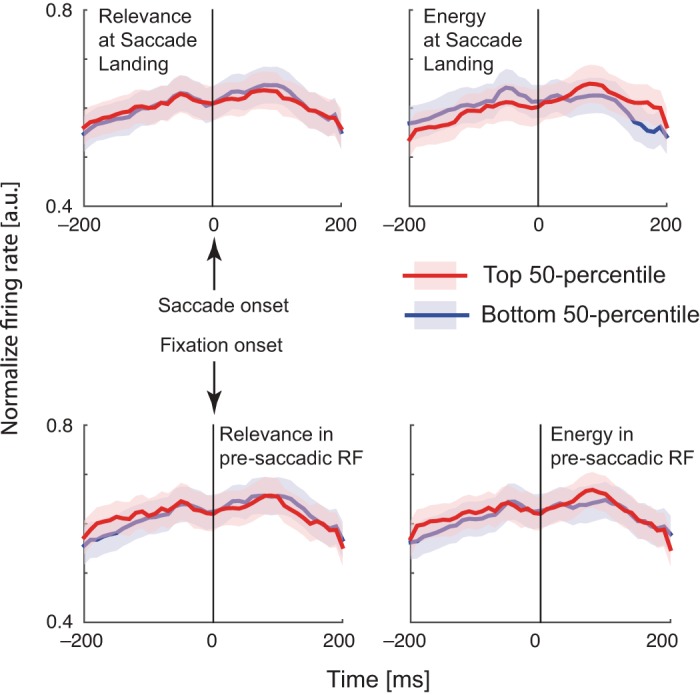
Relevance and edge energy do not modulate FEF firing rates around saccade onset (top) or fixation onset (bottom). We divided saccades into the top and bottom 50 percentiles of the respective visual features either at the saccade landing (top) or within the presaccadic receptive field (bottom), and calculated the saccade (top)- or fixation (bottom)- aligned PSTHs for each neuron separated in eight directional bins. To combine these across neurons, we then selected the directional bin with highest peak firing rate to represent the receptive field, and averaged the within-RF PSTHs across neurons to compute the saccade-aligned PSTHs (see methods). For fixation-aligned PSTHs, we first averaged responses around fixation around the directional bins representing out-of RF saccades and then averaged these single-neuron PSTHs (see methods).

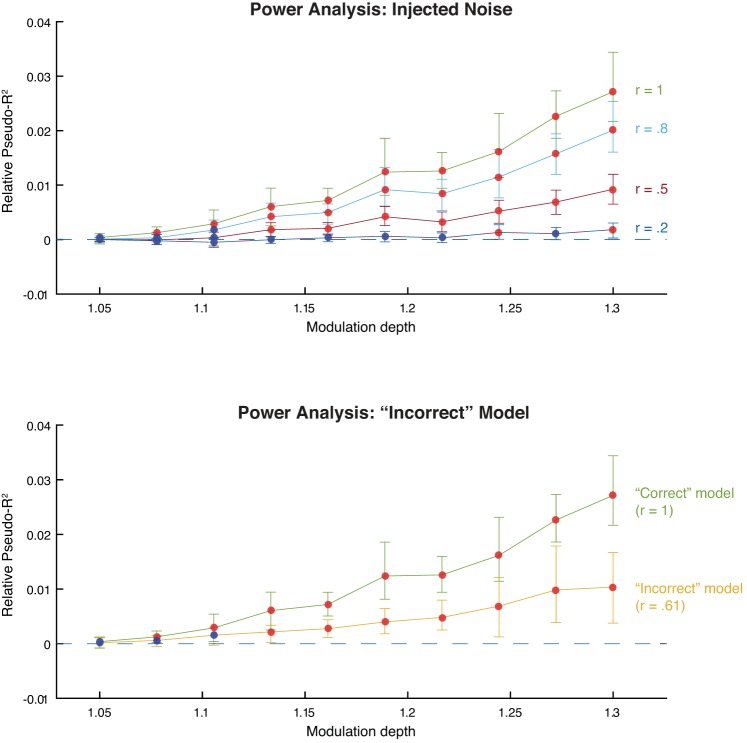
In summary, we found that upcoming movements, rather than relevant visual features, best explained neural activity in many neurons examined across all tasks. Could this result simply be due to a lack of statistical power? Neural representations of visual features are likely more complicated and weaker in natural scenes than in simple, artificial scenes. To address this possibility, we performed a power analysis based on simulated neural data. In short, we used behavioral data from a real experimental session to simulate many versions of neural data with different modulatory influences. We then fit this data with our model to ask if these influences were detectable (see methods). We found that, even when the simulated modulation depth (relative increase in firing rate; see methods) of relevance was low, we were able to detect its influence on neural activity (Fig. 10A, green line). Therefore, assuming our model of relevance representation is accurate, we would be able to detect relevance representations even when they were weak.

Fig. 10.

Power analysis. Both plots show marginal predictive power of relevance as a function of its simulated modulation depth. Red points indicate that the marginal predictive power is significantly greater than zero; blue points indicate that it is not significantly greater than zero. Error bars are bootstrapped 95% confidence intervals. A: injected noise analysis. After simulating the neural data, we corrupted the relevance model with varying degrees of noise and then fit the model. Each line represents the model fits for a different level of added noise. The r values indicate the correlation between the original model covariates and the corrupted model covariates. B: “Incorrect” model analysis. We simulated neural data using edge energy and fit the model using the relevance model (yellow line). For comparison, we include the model fits when the “correct” model, relevance, was used to simulate the spikes (green line).

However, what if our model of relevance is not accurate? The monkeys may use visual features to locate the target that are similar but not identical to our convolution-based relevance measure. To explore this issue, we performed two additional power analyses to ask whether we could detect the influence of relevance on neural activity. Both analyses make use of the following approach: we use one set of covariates to simulate the neural data and a different set of covariates to fit the model to the data. This procedure mimics the situation in which we have only approximate information about the relevance model that the monkey is using. In the first analysis, we used our standard relevance model covariates to simulate the neural data but fit the model using relevance model covariates that were corrupted with noise (see methods). Although our ability to detect the influence of relevance was decreased, detection required a stronger modulation depth of relevance, this modulation depth was still physiologically plausible (Fig. 10A). For example, even when the correlation between the relevance models for simulating and fitting was only .5, we could detect relevance when its modulation depth was ∼1.13 (compared with ∼1.08 when no noise was added; Fig. 10A, red line).

In the second analysis, we used two qualitatively different models for simulating and fitting the model. We simulated neural data using edge energy (see methods for definition) and fit the model using our convolution-based measure of relevance. Although not identical, edge energy and relevance are correlated (e.g., r = 0.61 for the Gabor search task), meaning that we should nonetheless be able to detect its influence. Our ability to detect relevance was indeed decreased, but not beyond physiological plausibility. More specifically, we could detect “relevance” when its modulation depth was ∼1.13, even though a qualitatively different model (edge energy) produced the data. Therefore, we find that our method of estimating the influence of relevant visual features on neural activity is robust to both weak effects and inaccurate models of relevance. Our inability to find relevance representations in the real data suggests that it is represented very weakly or that it is represented in a more complex manner than our bilinear spatiotemporal model can describe.

DISCUSSION

In this study, we used a modeling-based approach to analyze the FEF of monkeys while they searched complex, natural scenes. They searched for a target known ahead of time, making it possible for them to guide their saccades using target-similar features (task relevance). We then asked if FEF reflected feature-based attention, i.e., whether neural activity was explainable using task relevance and edge energy. We found that FEF activity was explained primarily by upcoming eye movements (a proxy for spatial selection or planning) and not by task relevance (a proxy for feature-based attention), or bottom-up influences such as saliency and energy.

Studies investigating the neural basis of feature-based attention have implicated the FEF in feature-based attention (e.g., Zhou and Desimone 2011). However, a recent study by the same group (Bichot et al. 2015) implicates a relatively unexplored region (but see Kennerley and Wallis 2009) in the prefrontal cortex, the VPA, as the primary source of feature-based attention. They showed that pharmacologically inactivating the VPA interfered with feature-based search behavior and also eliminated the signature of feature-based attention in FEF activity, while leaving the signature of spatial selection unaffected. This revised understanding of the role of FEF in attention may explain why we did not find a clear reflection of feature-based attention in FEF activity.

Our study thus raises the question of how results from simplified stimuli and tasks generalize to complex, natural vision. Beginning with the pioneering studies of Bruce and Goldberg (Goldberg and Bruce 1990; Bruce and Goldberg 1985, Bruce et al. 1985), many studies have implicated the FEF in planning saccades (Schlag-Rey et al. 1992; Thompson et al. 1997; Murthy et al. 2001), employing covert attention (Zhou and Desimone 2011; Moore and Fallah 2004), and selecting salient (Thompson and Bichot 2005; Schall et al. 1995; Schall and Thompson 1999) and task-relevant objects from distractors (Schall and Hanes 1993). While these studies have provided the foundation of our understanding about FEF function, they have typically used simplified tasks (involving a single cued saccade) in the context of artificial stimuli (that present limited choices against a homogeneous background). By contrast, natural scene search requires navigating hundreds or thousands of distracting stimuli and often requires making tens of self-initiated saccades. In support of these differences being important, a recent study from our group found that FEF activity is better explained by upcoming eye movements than visual saliency (Fernandes et al. 2014). The current study extends this work by examining the influence of top-down, rather than bottom-up, visual features on FEF activity. A central component of feature-based attention is a top-down bias for target-like objects, which is exactly what we failed to detect. Our study thus provides another line of evidence that FEF function may differ in the context of natural behavior and stimuli.

One important limitation of this study is the weak effect of relevant visual features on search behavior. The main implication of this weak effect is that if our relevance metric does not accurately model the search strategy used by monkeys to plan their saccades, then the brain may not reflect relevance. Although we found that the predictive power of relevance on search behavior varied across animals and tasks, relevance failed to predict firing rate changes. Despite this, we found, using simulations, that both noisy and incorrect definitions of relevance in our model were able to estimate the simulated effects on firing rates. Furthermore, despite this weak effect of relevance, when monkeys used relevance to inform saccade selection, they were more likely to be successful in finding the target (Table 3). Therefore, it is important to test the possibility that relevance modulates neural activity during saccade planning.

Our difficulty in predicting fixation choice with high accuracy suggests that better models of behavior are likely to be more successful in discovering the role of FEF in feature-based attention during naturalistic vision. However, even cutting-edge behavioral models of gaze achieve modest predictive power (for instance, see Borji et al. 2013 for a review of contemporary saliency models; best AUC < 0.6). These numbers highlight the difficulty of modeling complex, natural behaviors. Indeed, fixation choice is likely driven by many factors beyond relevant and salient visual features. Furthermore, not all saccades in a natural scene are made to locations that maximize immediate expected reward. Some saccades are corrective saccades, bridging the discrepancy between intended and current gaze locations in a sequence (Findlay 1982; Zelinsky 2008; Zelinsky et al. 1997). Other saccades are exploratory or information-gathering in intent, which are useful to maximize long-term expected reward (Najemnik and Geisler 2005; Gottlieb et al. 2013). These possibilities suggest that improved behavioral models of gaze as well as improved models of neural coding of behavioral variables might yield more success in understanding the computational role of the FEF during search. For example, more sophisticated models could incorporate the need to balance exploring the scene with exploiting particular image patches, or take into account the shifting spatial spotlight of covert attention.

Recent studies with natural scenes, including our own (Burman and Segraves 1994; Fernandes et al. 2014), have suggested that FEF may not encode visual information that is not targeted by an upcoming saccade. Such studies have called into question the conventional understanding that FEF represents a feature-based priority map. These findings need to be reconciled with findings from artificial tasks. What explains the discrepancy between results from artificial scenes and our findings using natural scenes? One possible explanation arises from the number of potential saccade targets in complex natural stimuli. In artificial search tasks with few saccade targets (typically fewer than 8), it may be possible to deploy covert attention to all of them. Therefore, selecting the saccade target based on its similarity to the search target is a feasible strategy, and FEF activity might reflect this similarity. In crowded natural scenes, by contrast, the space of possible saccade targets is continuous (infinite). In these contexts, it might only be feasible to attend to a local region around the point of fixation using feature-based attention. If this were true, the animal is more likely to be successful by making several saccades to new areas to maximize the likelihood of finding the target within these parafoveal regions. Therefore, during natural scene search, FEF activity might primarily reflect spatially selected saccade landings.

Another important discrepancy between artificial and natural search tasks arises from the natural behavior elicited by our tasks. Several studies with artificial stimuli have described an evolution of FEF activity from stimulus selection to saccade selection, suggesting distinct roles and classes of neurons in the continuum between representing visual and movement variables (Sato and Schall 2003; Schall and Thompson 1999; Schall et al. 1995). In our study, rather than holding fixation, the monkeys were allowed to freely move their eyes to locate targets. Hence, they are likely to immediately saccade to a target (or relevant stimulus) once it is detected. This means that target detection and making saccades to the target are likely to be tightly coupled during natural behavior. This close natural overlap between saccade decision and execution makes it challenging to disambiguate neural activity specifically related to each.

In summary, our results suggest that, during natural vision, the FEF does not reflect feature-based attention. We emphasize that upcoming eye movements explain away the effects of visual features on FEF activity. It is not the case that we failed to explain FEF activity, but rather that upcoming eye movements provide a better explanation than task-relevant visual features. These results suggest that FEF activity more closely reflects movement than sensory variables during natural scene search. They also expose an important need to develop better models of gaze behavior during natural scene search. More broadly, our study illustrates the complexity of understanding the role of higher-order brain areas during unconstrained, natural behaviors.

GRANTS

This work was supported by National Eye Institute Grant 1R01-EY-021579-01A1 (to M. A. Segraves and K. P. Kording).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

P.R., P.N.L., J.I.G., D.K.W., A.N.P., M.A.S., and K.P.K. conception and design of research; P.R., P.N.L., J.I.G., D.K.W., and A.N.P. performed experiments; P.R., P.N.L., J.I.G., and D.K.W. analyzed data; P.R., P.N.L., J.I.G., D.K.W., M.A.S., and K.P.K. interpreted results of experiments; P.R. and P.N.L. prepared figures; P.R. and P.N.L. drafted manuscript; P.R., P.N.L., J.I.G., D.K.W., M.A.S., and K.P.K. edited and revised manuscript; P.R., P.N.L., J.I.G., D.K.W., M.A.S., and K.P.K. approved final version of manuscript.