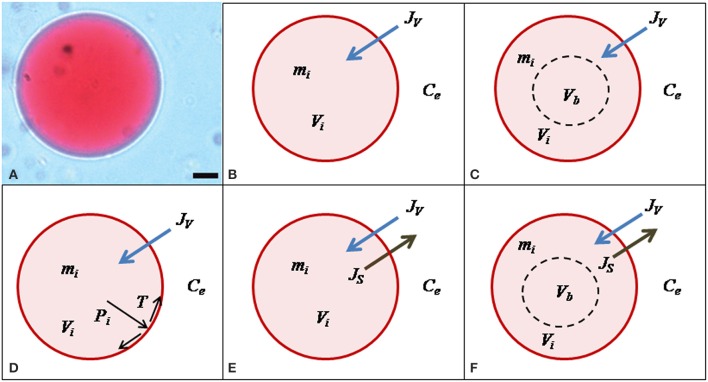
Figure 2.

Mathematical models of vacuole volume dynamics. (A) Microscopic image of a single Beta vulgaris root vacuole under iso-osmotic conditions; scale bar = 10 μm. (B) The W model assumes that only water moves across the membrane of the vacuole, thus the only parameter is P_f. (C) The WNOV model also considers that only water moves across the membrane but part of the vacuole volume is not involved in the osmotic response (V_b). This model also has two parameters: P_f and V_b. (D) The general model for water flow considers that J_V can be consequence of the combined effects of osmotic (Δosm) and hydrostatic (ΔP) driving forces. In the WME model, ΔP was determined by the elastic modulus of the membrane (ε) and the volume change (ΔV) of the vacuole, in a hypo-osmotic medium. This model has two parameters: P_f and ε. (E) The WS model considers that water and solute fluxes (J_V and J_s, respectively) are driven by the osmotic gradient (Δosm) and all the volume of the vacuole (V_i) is active. This model has two parameters: P_f and P_s. (F) The WSNOV model considers that besides the inactive volume V_b the internal mass of solutes (m_i) can be modified by the solute flux (J_s). This model has three parameters: P_f, P_s, and V_b. For a detailed description of these models see the text.