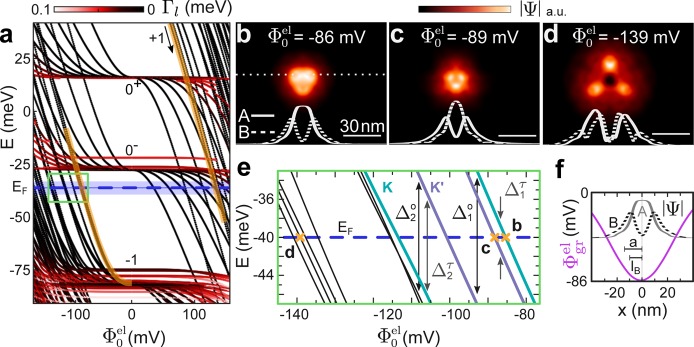
Figure 4.

(a) Tight binding eigenenergies of a 120 × 100 nm ² graphene sample with open boundaries as a function of tip-induced potential amplitude Φ₀^el at B = 7 T with the tip-induced potential centered on an AB area (BA and AA yield very similar behavior, not shown). Line color encodes coupling to the boundary (imaginary part Γ_l of eigenenergies); black (red) indicates strong (weak) localization underneath the tip. States from LL_±1 and the split LL₀ are labeled by ±1 and 0, respectively. The LL₀ splitting reduces the confining gap to E_0^– – E_–1 ≈ 50 meV. First states crossing E_F from LL_±1 are highlighted in orange. Uncertainty in E_F indicated as blue horizontal bar (Supporting Information). The green rectangle marks the zoom shown in panel e. (b–d) Color plot of the wave function amplitude 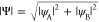of states marked by orange crosses in panel e. Φ₀ at the crossing point ε_l(Φ₀^el) = E_F is marked. Solid (dashed) white lines are line cuts along the dotted white line in panel b for contributions from sublattice A (B), as marked. All scale bars identical. (e) Zoom into area marked by a green box in panel a. Colored lines identify valley K (cyan) and K′ (purple). Orange crosses mark crossing of E_F (blue dashed line) of selected states, which are displayed in panels b–d. First two orbital Δ_j and valley Δ_k^τ splittings marked by arrows. (f) Comparison of length scales: tip-induced potential, magenta; calculated wave function amplitude |Ψ| of first state crossing E_F (same as panel b) for sublattice A (gray line) and B (dashed line); superstructure lattice constant a = 13.8 nm; magnetic length l_B (7 T) = 9.7 nm.