Fig. 1.

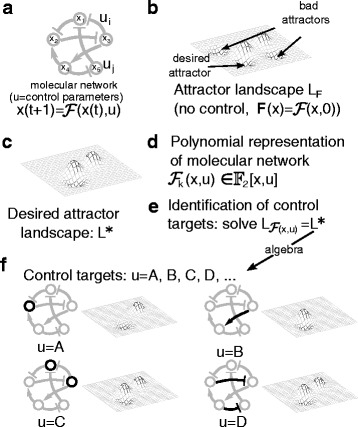
Description of the algebraic approach of identification of control targets. a. A BN model of a molecular network. The control variables are the entries of u. b. In the absence of control policies (u=0), the attractor landscape (L _F) can have undesirable attractors. c. The goal is to choose control values that give a desired attractor landscape, L ^∗. d. To use the algebraic approach we first find the polynomial representation of the BN (see Section Control Actions: edge and node manipulations). e. The next step is to set up the desired attractor landscape as a system of equations that the BN has to satisfy, $L_{\mathcal{F}(x,u)}=L^{\ast }$ (see Section Control targets in Boolean networksControl targets in Booleannetworks). f. Solving the equation $L_{\mathcal{F}(x,u)}=L^{\ast }$ for u will provide the control values to achieve the desired landscape (see Section Identifying control targets). This approach not only finds individual control policies (u=A, single node; u=B, single edge), but also combinatorial control policies (u=C, two nodes; u=D, two edges). In a combinatorial control policy, the desired attractor landscape is achieved by the combination of two or more entries of u