Integrative Bayesian Analysis of Neuroimaging-Genetic Data with Application to Cocaine Dependence

Abstract

Neuroimaging and genetic studies provide distinct and complementary information about the structural and biological aspects of a disease. Integrating the two sources of data facilitates the investigation of the links between genetic variability and brain mechanisms among different individuals for various medical disorders. This article presents a general statistical framework for integrative Bayesian analysis of neuroimaging-genetic (iBANG) data, which is motivated by a neuroimaging-genetic study in cocaine dependence. Statistical inference necessitated the integration of spatially dependent voxel-level measurements with various patient-level genetic and demographic characteristics under an appropriate probability model to account for the multiple inherent sources of variation. Our framework uses Bayesian model averaging to integrate genetic information into the analysis of voxel-wise neuroimaging data, accounting for spatial correlations in the voxels. Using multiplicity controls based on the false discovery rate, we delineate voxels associated with genetic and demographic features that may impact diffusion as measured by fractional anisotropy (FA) obtained from DTI images. We demonstrate the benefits of accounting for model uncertainties in both model fit and prediction. Our results suggest that cocaine consumption is associated with FA reduction in most white matter regions of interest in the brain. Additionally, gene polymorphisms associated with GABAergic, serotonergic and dopaminergic neurotransmitters and receptors were associated with FA.

1 Introduction

Cocaine use is associated with several acute effects on a variety of intracellular pathways such as inhibition of the serotonin, dopamine, and norepinephrine transporters (Han and Gu, 2006). Chronic use of cocaine leads to addiction, which inflicts high costs to individuals and society. Long-term drug addiction is known to cause many health problems, both psychological (depression, paranoia, anxiety) and physical (cardiac disease). Although genetics contribute substantially to addiction vulnerability, the identification of genes associated with this susceptibility has been slow (Li and Burmeister, 2009). Several studies have suggested that certain DNA polymorphisms may impact the extent to which a person is vulnerable to drug abuse and addiction (Nielsen and Kreek, 2012; Kreek et al., 2005b), and may have significant effects on an individual’s response to treatment (Berrettini and Lerman, 2005; Kreek et al., 2005a; Nielsen et al., 2014; Bauer et al., 2014).

Recent advances in imaging technologies such as positron emission tomography (PET), functional magnetic resonance imaging (fMRI), and diffusion tensor imaging (DTI) have enabled non-invasive investigation of neurochemical, functional and structural alterations in the brains of drug-addicted subjects, revealing new insights into the mechanism of addiction (Volkow et al., 2003). Chronic cocaine users have been shown to exhibit subtle abnormalities in different areas of the brain, as measured by DTI (Lim et al., 2008; Moeller et al., 2007; Lane et al., 2010; Moeller et al., 2005; Ma et al., 2009; Romero et al., 2010; Liu et al., 2008). These areas include the anterior and posterior corpus callosum and tracts in the frontal and parietal regions of the brain. In addition, cocaine has been shown to alter the methylation of myelin genes in rodents (Nielsen et al., 2012b). However, the precise mechanisms that cause alterations in white matter remain unknown.

The search for genetic factors associated with a disease is complicated due to the intrinsic confluence of genetic, epigenetic (Nielsen et al., 2012c), environmental and psychological components as well as additional factors that may not have been defined (Craig et al., 2008). Understanding the links between genetics, brain structure and function is an inherently multidisciplinary endeavor that has broad implications for a number of medical disorders, including neurological conditions such as Alzheimer’s disease (Kohannim et al., 2011; Braskie et al., 2011), autism (Dennis et al., 2011), bipolar disorder (Frazier et al., 2014), obesity (Ho et al., 2010), and schizophrenia (Braskie et al., 2012).

Statistical integration of imaging and genetic data for investigating brain-wide, candidate-gene associations is challenging because the method of inference must account for (i) spatial dependence among the high-dimensional measurements of imaging phenotypes; (ii) multiplicity adjustments among the numerous tests; and (iii) model uncertainty in the presence of a large set of genetic factors. For example, even with a relatively modest number of genetic variables, such as 23, our study yields a prohibitively large number of possible models (more than 8 million) for conducting inference at a single voxel. Moreover, we expect associations to be spatially heterogeneous across brain regions due to varied functional and physical features, which thereby precludes inference using any single model applied uniformly to all voxels in the brain (which is typically in the hundreds of thousands).

Various statistical methods have been used to examine relationships between genetics and brain imaging features. Multivariate generalized linear modeling is commonly used to identify associations among multivariate phenotypes and candidate genotypes (Chung et al., 2010; Taylor and Worsley, 2008; Worsley et al., 2004). Component-wise methods offer alternatives that use univariate analysis for each component, with multiplicity control through post hoc application of Bonferroni correction, false discovery rates, or random field theory to adjust for multiple comparisons (Heller et al., 2007; Lazar et al., 2002). Principal component analysis is another approach that is used to reduce the dimension of the multivariate phenotype (Formisano et al., 2008; Teipel et al., 2007; Rowe and Hoffmann, 2006; Kherif et al., 2002). In addition, sparse reduced rank regression is often implemented in brain-wide, genome-wide association studies (Vounou et al., 2010). Partial least squares regression can be used to identify linear projections of the multivariate phenotype and genotype on lower dimensional spaces (Chun and Keleş, 2010; Krishnan et al., 2011). The effects of multiple genes can be modeled nonparametrically using least squares kernel-based learning methods (Liu et al., 2007; Ge et al., 2012).

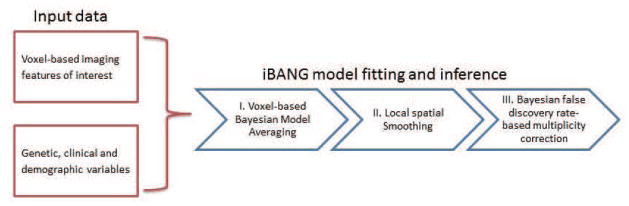
The aforementioned statistical methods currently available for voxel-wise analysis fail to account for uncertainty in model selection, and thus are limited for detecting associations between brain features and a large set of genetic covariates that may vary over the volume of interest. In addition, these methods do not allow for the explicit quantification of model uncertainties. To overcome these limitations, we developed a statistical framework that enables probabilistic inference for voxel-wise analysis that leverages Bayesian model averaging procedures. This allows us to not only quantify the genetic associations, but also to explicitly calculate uncertainties in terms of posterior probabilities, which admits precise multiplicity controls for coherent inference and variable selection. Briefly, our framework for integrative Bayesian analysis of neuroimaging-genetic (iBANG) features circumvents the high-dimensional problem by decoupling model fitting and inference. We first conduct a voxel-based Bayesian model averaging procedure, in parallel, to generate posterior probability maps for each genetic variable spanning the entire brain. Subsequently, we incorporate spatial information into our inferential techniques by locally smoothing the probability maps. Finally, we demarcate specific regions of association using multiplicity-corrected false discovery rates. This allows our methods to scale to large datasets as well as provide principled statistical inference while accounting for various sources of variability induced by model selection and spatial heterogeneity. Furthermore, we demonstrate the benefits of accounting for model uncertainties in both model fit and prediction. Figure 1 is a schematic representation of our modeling strategy.

Figure 1.

Schematic representation of iBANG model and analysis

Our methods are applied to data from a recent cocaine addiction study (see Section 2 for details) that sought to identify brain regions that exhibit strong evidence of differential diffusion patterns among candidate genetic variants, cocaine users, and demographic covariates using FA in the white matter space as defined by the Montreal Neurological Institute (MNI). Our framework is general enough to be applied to any imaging modality to conduct voxel-wise analyses of specific imaging parameters and outcomes of interest.

The structure of our article is as follows: Section 2 summarizes the main aspects of the cocaine addiction study, including the target population and acquisition of brain images and genetic data. Section 3 details the iBANG methodology and Section 4 presents the neurobiological findings from the integrative analysis. Section 5 provides a discussion of the assumptions, implications, and possible extensions of our work. Additional technical, computational and analytic details and results are provided in the supplementary materials.

2 Motivating Data

2.1 Study population

Study participants were recruited to the Center for Neurobehavioral Research on Addictions at the University of Texas Health Science Center at Houston through advertisements for research volunteers. All individuals with cocaine dependence and all non-drug users (controls) were screened for psychiatric and non-psychiatric medical disorders using the Structured Clinical Interview for DSM-IV (First et al., 1996). The study population included 39 cocaine users (29 male and 10 female users) and 19 control participants (12 male and 7 female controls). Table 1 lists the characteristics of the study population. This study was approved by the Institutional Review Boards of the University of Texas Health Science Center and Baylor College of Medicine, as well as the Research and Development committee of the Michael E. DeBakey Veteran Affairs Medical Center.

Table 1.

Characteristics (mean and range) of study population of cocaine users and controls.

	Control group(N=19)	Cocaine group(N=39)
Sex (% male)	63	74
Age (years)	32.69 (21 – 48.8)	40.38 (22.7 – 54.8)
Education (years)	14.16 (11 – 18)	12.85 (10 – 16)
Lifetime cocaine use (years)	0	13.83 (2 – 30)
Cocaine use (days per prior month)	0	14.77 (2 – 30)
Ethnicity (% African American)	84	51

2.2 Brain image acquisition and processing

Whole brain diffusion-weighted images (DWI) were acquired on a Philips 3.0 T Intera system with a six-channel phased array receiver head coil (Philips Medical Systems, Best, Netherlands). Images were acquired in the transverse plane using a single-shot spin-echo diffusion sensitized echo-planar imaging (EPI) sequence (bfactor=1000 s/mm², repetition time=6100 ms, echo time=84 ms, 44 contiguous axial slices, field-of-view= 240 mm × 240 mm, 112 × 112 acquisition matrix, 256 × 256 reconstructed matrix, 0.9375 mm × 0.9375 mm reconstructed in-plane resolution, slice thickness=3 mm). The diffusion tensor encoding scheme is based on the uniformly distributed and balanced rotationally invariant Icosa21 tensor-encoding set (21 gradient directions) (Hasan et al., 2001). A SENSE acceleration factor or kspace under sampling was set to be R=2 to reduce EPI image distortions. The diffusion-encoded volumes were acquired with fat suppression. The acquisition time was approximately 7 minutes and resulted in signal-to-noise ratio independent DTI-measure estimation (Hasan, 2007). All the DTI images were processed using the FMRIB Software Library (www.fmrib.ox.ac.uk/fsl, version 5.04) (Jenkinson et al., 2012). For each scan, the DWI images were corrected for eddy current distortions and head motion (Jenkinson and Smith, 2001) after converting the Philips DICOM files into NIfTI format using dcm2nii. Then, brain was extracted from the images using FSL’s Brain Extraction Tool (BET) (Smith, 2002). Next, the FMRIBs Diffusion Toolbox (FDT/FSL) (Behrens et al., 2003) was used to fit the data to extract FA and other DTI parameters for each voxel. All the FA images were aligned to the standard MNI space using the FSL’s nonlinear registration (Andersson et al., 2007a,b) with the FMRIB58-FA template image.

2.3 Genetic data acquisition

Twenty-one candidate genetic variants in seventeen genes that we had hypothesized may play a role in the vulnerability to develop addiction, have previously been associated with addiction vulnerability, known to be involved in psychiatric morbidities, or in neurotransmitter pathways were examined. These have been assessed in prior studies (Nielsen et al., 2012a; Kosten et al., 2013b,a; Spellicy et al., 2013; Kosten et al., 2013b, 2014; Anastasio et al., 2014; Spellicy et al., 2014; Frazier et al., 2014; Liu et al., 2014; Brewer III et al., 2015). This includes several polymorphisms in the dopamine and serotonin transporters, and in the norepinephrine postsynaptic receptor. Genotypes were coded as 0 or 1 following the dominant model. The list of genetic variants, genetic descriptions and genotype coding are given in Table 2.

Table 2.

Genetic Summary: first column presents the list of variant in the study; second column shows SNPs and Insertion/Deletion; third column indicates gene symbol; fourth column presents gene name; and fifth column is genotype coding .

Genetic variant	SNPs	Gene symbol	Gene name	Code
HTR2A	rs6311	HTR2A	5-hydroxytryptamine (serotonin) receptor 2A, G protein-coupled	(GG=0),(AG,AA=1)
HTR2C	rs6318	HTR2C	5-hydroxytryptamine (serotonin) receptor 2C, G protein-coupled	(GG=0),(CG,CC=1)
TPH1	rs1799913	TPH1	tryptophan hydroxylase 1	(GG=0),(GT,TT=1)
TPH2	rs4290270	TPH2	tryptophan hydroxylase 2	(AA=0),(AT,TT=1)
MAOB	rs1799836	MAOB	monoamine oxidase B	(CC=0),(CT,TT=1)
DRD2a	rs6277	DRD2	dopamine receptor D2	(GG=0),(AG,AA=1)
DRD2b	rs2283265	DRD2	dopamine receptor D2	(CC=0),(AC,AA=1)
DBH	rs1611115	DBH	dopamine beta-hydroxylase (dopamine beta-monooxygenase)	(CC=0),(CT,TT=1)
COMT	rs4680	COMT	catechol-O-methyltransferase	(GG=0),(AG,AA=1)
TH	rs10770141	TH	tyrosine hydroxylase	(GG=0),(AG,AA=1)
HTR1A	rs6295	HTR1A	5-hydroxytryptamine (serotonin) receptor 1A, G protein-coupled	(CC=0),(CG,GG=1)
GAD1a	rs1978340	GAD1	glutamate decarboxylase 1 (brain, 67kDa)	(GG=0),(AG,AA=1)
GAD1b	rs769390	GAD1	glutamate decarboxylase 1 (brain, 67kDa)	(AA=0),(AC,CC=1)
ADRA1A	rs1048101	ADRA1A	adrenoceptor alpha 1A	(GG=0),(AG,AA=1)
ADRA1D	rs2236554	ADRA1D	adrenoceptor alpha 1D	(TT=0),(AT,AA=1)
CHRNA5	rs16969968	CHRNA5	cholinergic receptor, nicotinic, alpha 5 (neuronal)	(GG=0),(AG,AA=1)
BDNF	rs6265	BDNF	brain-derived neurotrophic factor	(CC=0),(CT,TT=1)
	Insertion/Deletion
SLC6A4a	5-HTTLPR in promoter	SLC6A4	solute carrier family 6 (neurotransmitter transporter), member 4	(LL=0),(LS,SS=1)
SLC6A4b	17-bp VNTR in intron 2, STin2	SLC6A4	solute carrier family 6 (neurotransmitter transporter), member 4	{(12, 12) = 0}, {Other = 0}
SLC6A3a	40-bp VNTR in the 3’ UTR exon 15	SLC6A3	solute carrier family 6 (neurotransmitter transporter), member 3	{(10, 10) = 0}, {Other = 0}
SLC6A3b	30-bp VNTR in intron 8 (Int8 VNTR)	SLC6A3	solute carrier family 6 (neurotransmitter transporter), member 3	{(6, 6) = 0}, {Other = 0}

3 Methods

In this section, we introduce iBANG, a method for integrative Bayesian analysis of neuroimaging-genetic data. The statistical method is motivated by the use of FA values acquired in voxels in the MNI white matter space that spans the entire brain. However, the framework is quite general and can be used for integrative analysis of any continuous image-derived parameters.

3.1 iBANG model formulation

Suppose that the imaging feature (e.g., FA values) at voxel ν = 1, . . . , V for subject i = 1, . . . , n is represented as y_i(ν) and the corresponding (k-dimensional) genetic and demographic variables are represented as x_i1, . . . , x_ik. Assume Y (ν) is a column-wise matrix of imaging features {y₁(ν), . . . , y_n(ν)} , X is a n × k matrix, and β(ν) is the full k-dimensional vector of regression coefficients. The linear regression model for the νth voxel is

$$\mathit{Y}(\nu )=\alpha +\mathit{X}\mathit{\beta }(\nu )+\sigma \mathit{\epsilon },$$ (3.1.1)

where α is an intercept, σ ∈ ℝ₊ is a scale parameter, and ε is random noise (accounting for unknown sources of variation), which follows an n-dimensional normal distribution with zero mean and the identity covariance matrix. Our primary construct for inference is the effect surfaces β(ν)’s that capture the associations between the imaging features and each of the k covariates across the brain. However, this requires estimation of V × k number of parameters, which in our case is 3×10⁶×24 ≈ 72 million parameters without accounting for model uncertainty, which represents considerable analytical and computational challenges. Subsequently, accounting for model uncertainty over all possible models, this number increases exponentially to 3 × 10⁶ × 2²⁴. While Bayesian model averaging (BMA) involves more effective parameters, by explicitly accounting for model uncertainty, BMA both shrinks the influence of certain variables to zero through the model weights and provides an unified method of inference for all voxels. Therefore, the BMA approach when applied in this context eschews the dilemma posed by implementation of voxel-wise model selection procedures, which can yield a joint inference that utilizes discordant models at adjacent voxels, and thereby neglects spatial dependence in the model space. To address this, we decouple the model fitting and inference using a three-step component-wise analysis pipeline:

• Step I: Estimate the association between each genetic and demographic variable via voxel-based Bayesian model averaging and obtain posterior probability maps (PPMs) of the associated genetic and demographic features for each covariate.

• Step II: Incorporate spatial information pertaining to voxel locations to smooth the PPMs using prefiltered rotationally invariant nonlocal means to generate smoothed posterior probability maps (sPPMs) of the associated genetic and demographic variables.

• Step III: Conduct rigorous inference on the sPPMs of the genetic and demographic variables using Bayesian false discovery rates to delineate regions of brain activation while controlling for multiplicities.

We detail each of these steps below.

3.1.1 Bayesian model averaging

BMA is a tool used to enumerate model uncertainty by averaging across the best models using each model’s posterior probability as weights. BMA considers all 2^k subsets of possible explanatory variables in the analysis but shrinks the influence of certain variables to zero through the model weights (Raftery, 1995). Denoting the space of all 2^k possible models by ℳ = {M_j : j = 1, . . . , 2^k}, a specific model M_j has a subset of X_j clinical, demographic and genetic variables, leading to the following reduced equation:

$$\mathit{Y}(\nu )=\alpha +{\mathit{X}}_j{\mathit{\beta }}_j(\nu )+\sigma \mathit{\epsilon }$$ (3.1.2)

where β_j ∈ ℝ^k_j (0 ≤ k_j ≤ k) is the reduced subset of covariates from (3.1.1) with the exclusion of a regressor indicating that the corresponding element of β_k−kj (ν) is zero.

Priors

To conduct Bayesian inference, prior distributions need to be defined for the model space ℳ and the corresponding parameters β, α and σ. The choice of prior distributions could significantly impact the resulting posterior model probabilities, thereby necessitating careful consideration (Kass and Raftery, 1995; Hoeting et al., 1999; Raftery, 1995; Friston and Penny, 2003). We consider improper noninformative priors for the parameters common to all models, namely α and σ, such that p(α, σ) ∝ σ⁻¹, allowing for maximal learning from the data. σ is the residual error variance, and thereby accounts for unknown sources of variability that are not attributable to the covariates. We assume a common prior for σ across the different models, which is the usual approach (Mitchell and Beauchamp, 1988; Raftery et al., 1997). Also, we consider a g-prior structure for β_j(ν) whereby p {β_j(ν)|α, σ, M_j} is modeled as a k_j-dimensional normal distribution with mean zero and covariance matrix of ${\sigma }^2{(g{\mathit{X}}_j^{\prime }{\mathit{X}}_j)}^{-1}$, where g = 1/max{n, k²}. The choice of g is based on theoretical considerations to guarantee asymptotic consistency for selecting the correct model, i.e., ensuring that the posterior probability of the correct model approaches 1 for increasing sample size (Fernandez et al., 2001a). Finally for model selection, we consider a prior distribution over all 2^k possible models. We denote the model probability for the jth model by p(M_j) = p_j, j = 1, 2, . . . , 2^k. We assume an uniform distribution on the model space to avoid a priori model preference in the absence of prior knowledge.

Posterior computations

The posterior distribution of β_j(ν) can be written as

$$\mathcal{P}\{{\mathit{\beta }}_j(\nu )\mid \mathit{Y}(\nu )\}=\sum _{j=1}^{2^k}\mathcal{P}\{{\mathit{\beta }}_j(\nu )\mid \mathit{Y}(\nu ),M_j\}\mathcal{P}\{M_j\mid \mathit{Y}(\nu )\}.$$ (3.1.3)

The second term ℘ {M_j|Y (ν)}, the posterior model-specific probability is calculated as follows

$$\mathcal{P}\{M_j\mid \mathit{Y}(\nu )\}=\frac{\{{\mathcal{L}}_{(\nu )}(M_j)\}P(M_j)}{{\sum }_{j=1}^{2^k}\{{\mathcal{L}}_{(\nu )}(M_h)\}P(M_h)},$$ (3.1.4)

where the marginal likelihood of model M_j, which we denote by ℒ_(ν)(M_j), is

$${\mathcal{L}}_{(\nu )}(M_j)=\int p\{\mathit{Y}(\nu )\mid \alpha ,{\mathit{\beta }}_j(\nu ),\sigma ,M_j\}p(\alpha ,\sigma )p\{{\mathit{\beta }}_j(\nu )\mid \alpha ,\sigma ,M_j\}d\alpha d{\mathit{\beta }}_j(\nu )d\sigma ,$$ (3.1.5)

where p {Y (ν)|α, β_j(ν), σ, M_j} represents the sampling model, (3.1.2), p(α, σ) and p {β_j(ν)|α, σ, M_j} are the priors distributions for the intercept, scale, and regression coefficients, respectively. The marginal likelihood can be obtained analytically (Fernandez et al., 2001a) as follows:

$${\mathcal{L}}_{(\nu )}(M_j)~{\left(\frac{g}{g+1}\right)}^{k_j/2}{\left(\frac{1}{g+1}\mathit{Y}{(\nu )}^{\prime }{D}_{X_j}\mathit{Y}(\nu )+\frac{g}{g+1}{(\mathit{Y}(\nu )-\overline{\mathit{Y}(\nu )})}^{\prime }(\mathit{Y}(\nu )-\overline{\mathit{Y}(\nu )})\right)}^{-(n-1)/2},$$ (3.1.6)

where $D_{X_j}=I_n-{\mathit{X}}_j{({\mathit{X}}_j^{\prime }{\mathit{X}}_j)}^{-1}{\mathit{X}}_j^{\prime }$ and $\overline{\mathit{Y}(\nu )}$ is the sample mean of response variable. We use Markov chain Monte Carlo (MCMC) based methods to estimate all model parameters and posterior probabilities. Details of the computational algorithms are briefly described below. Note that the BMA procedure is performed voxel-wise and hence can run simultaneously for each voxel, which allows the algorithm to be parallelized.

Estimation of model parameters and posterior probabilities using MCMC

In practice, computing the posterior probabilities is a challenge due to the large amount of summations involved in calculating the posterior probability maps (PPMs). In our application, we have k=24 possible clinic/demographic and genetic variables. Hence, we need to calculate the posterior probabilities for each 2²⁴ = 16777216 models and average the required distributions over all models. To ease the computational effort, we adopt the approach of (Madigan et al., 1995) and approximate the posterior distribution on the model space ℳ by applying MCMC frequencies obtained from a Metropolis-based sampler. Assuming that the chain is currently at model M_s which contains X_s regressors, and X_j denotes a (single) regressor which could include or exclude one of X_s regressors. A new model M_j was proposed randomly by sampling from an uniform distribution on the space containing M_s and all models with one variable more or less than M_s. So the number of regressors in M_j is X_s ± X_j. Two options are effectuated at each iteration of the sampling algorithm. The chain could move to M_j with probability $pr=\mathit{min}\{1,\frac{\mathcal{L}(M_j)P(M_j)}{\mathcal{L}(M_s)P(M_s)}\}$ or remain at model M_s with probability 1 − pr (see e.g. Fernandez et al., 2001b; Raftery et al., 1997, for implementations in the context of linear models). Additional details describing the MCMC software implementation and performance metrics such as mixing and computational times are provided in Section S1 of the supplementary materials.

3.1.2 Smoothing posterior probability maps by prefiltered rotationally invariant non-local means

The BMA procedure above yields voxel-wise PPMs of the clinical, demographic and genetic variables. To account for spatial correlation among voxels that is inherent to the PPMs, a post-hoc smoothing procedure is conducted to generate smoothed posterior probability maps (sPPMs) by borrowing strength from neighboring voxels. Standard (linear) smoothing approaches such as Gaussian kernels could be adopted here. While approaches based on Gaussian filters are capable of reducing image noise, especially in homogeneous areas, they tend to remove some high-frequency signal components as well, which produces images with blurred edges (Ashburner and Friston, 2000). In our context, this could have implications for identification of the resulting significant regions, as a simple Gaussian smoother may yield posterior probability maps with blurred edges.

We follow the method proposed by (Manjón et al., 2012) via prefiltered rotationally invariant nonlocal means (PRI-NLM3D). This method maintains domain and scale symmetry i.e since the raw (non-smoothed) posterior probabilities lie in the interval (0, 1) this method maps the (smoothed) probabilities on same interval (0, 1). This is especially helpful since all of our downstream analyses are based on the smoothed probabilities maps. Moreover, from the scale perspective, this technique is similar to the processing methods, since the original FA values are also in (0, 1).

This technique is a combination of the Oracel-based 3D discrete cosine transform (3D-DCT) and rotationally invariant nonlocal means (RI-NLM). The method offers several advantages, namely that it provides better smoothing performance around the edges and benefits from faster smoothing time in comparison to Oracel-based 3D-DCT and block-wise NLM. Let ℘(ν) denote the PPM of any variable on voxel ν. The PPM can be written as a sum of sPPMs, ℘_s(ν), plus white noise corresponding to voxel-based BMA analysis, which leads to:

$$\mathcal{P}(\nu )={\mathcal{P}}^s(\nu )+\eta$$ (3.1.7)

The smoothing process includes two steps:

• Step I: Pre-smoothing based on a three-dimensional moving-window DCT hard thresholding.

• Step II: Smoothing the pre-smoothed PPMs using a three-dimensional rotationally invariant version of the nonlocal means.

The main concepts of each step are explained in sequence below.

3D discrete cosine transform smoothing

The DCT is a similarity transformation. The advantage of this technique is robustness and absence of any assumptions concerning PPM statistics beyond sparsity (Guleryuz, 2007). Let ${\mathcal{P}}_1^s(\nu )$ denote a pre-smoothed posterior. A 3D block DCT (4×4×4 block size, which indicates data cubes) is used. We apply a hard threshold to obtain the local smoothed estimation at block b , ${\widehat{\mathcal{P}}}_b^s$, which is presented as

$${\widehat{\mathcal{P}}}_b^s=H^{-1}(\widehat{c_b}),\mathit{where}{c}_b=H({\mathcal{P}}_b),\text{and}\widehat{c_b}=T(c_b,\tau ),$$ (3.1.8)

where H represents a 3D DCT, c_b shows the transform coefficients for block b, and T is the hard thresholding operator with threshold τ. By combining all overlapping B blocks at the position of ν and following the weighted rule, we can derive the local estimator of ${\widehat{\mathcal{P}}}_1^s(\nu )$:

$${\widehat{\mathcal{P}}}_1^s(\nu )=\frac{{\displaystyle \sum _{b=1}^B}{\theta }_b{\widehat{\mathcal{P}}}_b^s(\nu )}{{\displaystyle \sum _{b=1}^B}{\theta }_b},\mathit{where}{\theta }_b=\frac{1}{1+{\Vert \widehat{c_b}\Vert }_0},$$ (3.1.9)

and B represents the number of overlapping blocks used to calculate ${\widehat{\mathcal{P}}}_1^s(\nu )$, and θ_b denotes a weight for block b, which is a propositional inverse of the ĉ_b L₀ norm. L₀ norm of ĉ_b corresponds to the number of nonzero coefficients of block b after the hard thresholding.

Nonlocal means smoothing

Nonlocal means (NLM) smoothing is defined on the basis of voxels with similar neighborhoods (small 3D volumetric patches) that tend to have similar posterior probability values (Buades et al., 2005). The NLM estimator of the smoothed posterior probability at voxel ν is defined as

$${\widehat{\mathcal{P}}}_2^s(\nu )=\frac{{\sum }_{\nu \in \mathrm{\Omega }}w(\nu ,{\nu }^{\prime })\mathcal{P}(\nu )}{{\sum }_{\nu \in \mathrm{\Omega }}w(\nu ,{\nu }^{\prime })},\text{where}w(\nu ,{\nu }^{\prime })=e^{-\frac{\Vert N_{\nu }-N_{{\nu }^{\prime }}\Vert }{h^2}},$$ (3.1.10)

and Ω represents the search volume, w(ν, ν′) represent the similarity weights for any two 3D patches N_ν and $N_{\nu }^{\prime }$ centered around voxels ν and ν′, and h² denotes the bandwidth, which determines the extent of the smoothing.

We use the PRI-NLM3D method to obtain ℘̂^s(ν), providing an sPPM for each clinical, genetic and demographic variable. The PRI-NLM3D method combines and extends the above steps. We implemented smoothing using an Oracle-based 3D-DCT to find the pre-smoothed PPM of each of the clinical and genetic variables and then applied the rotational invariant NLM to derive the sPPM, ℘̂^s(ν), for each variable (Manjón et al., 2012). We used the extended version DCT filter which is an Oracle-based DCT filter. It only has one parameter τ, and as recommended by Manjon et al (2012), we use τ = 2.7 * σ where σ is the estimated from the data as the standard deviation of random noise. The approach is similar to Discrete cosine transforms and wavelet thresholding methods of (Mallat, 1999). Additionally, we assume noise follows a Rician distribution (Nowak, 1999). The procedure is computationally inexpensive, with computation times of less than one minute when implemented using the PPMs that resulted from the cocaine study, for each of the 24 maps consisting of close to 300,000 voxels.

3.1.3 Bayesian false discovery rate controls for identification of significant voxels

The primary objective of this type of integrative analysis is to identify brain regions that exhibit strong evidence of differential activation patterns in the presence or absence of genetic and clinical and demographic factors. After implementing the Bayesian model averaging and smoothing steps, we obtain a smoothed posterior probability map for each variable spanning the entire brain region. Owing to the high-dimensional nature of the these neuroimaging phenotypes, the process for delineating significant voxels requires hundreds of thousands of tests, thereby running the risk of detecting thousands of false positive findings by random chance alone, in the absence of adequate multiplicity corrections. The false discovery rate (FDR), or the expected proportion of false positives voxels among all voxels deemed significant, can be controlled in this context through the specification of a threshold for the Bayesian posterior p-value (sometimes referred to as a q-value), (Storey, 2003). The generation of sPPMs from the aforementioned modeling steps admits a straightforward and computationally efficient strategy to implement FDR controls. Specifically, we assume that all voxels for which the resulting sPPM exceeds a given threshold ϕ, ℘̂^s(ν) > ϕ, characterize locations for which the imaging phenotype is significantly affected by changes in a given genetic variant. Considering the cocaine study, let χ_ϕ = {ν : ℘̂^s(ν) > ϕ} represents the set of all significant voxels for a given genetic variant. The significant threshold ϕ can be set to control the Bayesian FDR (Morris et al., 2008; Baladandayuthapani et al., 2010). Suppose that ϕ_δ denotes the threshold value that controls the overall average FDR at level δ. Posterior inference using ϕ_δ implies that given the available evidence, we expect only 100δ% of the total number of voxels that are declared significant to represent false-positive locations for which the imaging phenotype is truly unaffected by a given covariate. For all sPPMs, we sort ℘̂_κ = ℘̂^s(ν_κ) in ascending order to yield ℘̂_(κ), κ = 1, . . . , ν. Assume κ^* is a count of the number of voxels, with sPPM exceeding the threshold. Then, ϕ_δ = ℘̂(ξ), where $\xi =\mathit{max}\{{\kappa }^{\ast }:{\kappa }^{\ast -1}{\sum }_{\kappa =1}^{{\kappa }^{\ast }}1-{\widehat{\mathcal{P}}}_{(\kappa )}\le \delta \}$. We use χ_ϕδ; to denote the final set of voxel locations that yield evidence of an effect that significantly impacts the FA based on the average Bayesian FDR control at level δ. Note that ϕ may also be specified in consideration of the utility/loss functions such as relative cost of a false-positive versus a false-negative error (Müller et al., 2004).

4 Application to neuroimaging-genetic data in cocaine addiction study

In this section, we present the results of our integrative analysis of the neuroimaging-genetic data obtained from the cocaine addiction study. The iBANG method described in Section 3 was used to identify regions of brain that exhibit strong evidence for differential diffusion patterns among the candidate genetic variants and demographic variables. Before model fitting, each patient’s scan was registered to a common brain. Voxels contributing FA values that exceed 0.2 were used in the analysis to capture white matter regions of brain. This resulted in a total of 293,318 voxels for downstream analyses. The analysis involved the three sequential components as described in the methods section. Implementation of step 1 used the BMS package in statistical software R (see Section S1 of the supplementary materials for more details). Step 2 was implemented using the MRI Denoising Matlab toolbox (Manjón et al., 2012). Multiplicity correction was used thereafter to control the rate of false positives at 10%. The elapsed time for analysis of one voxel was 3.894 seconds. For ease of exposition, our results are summarized in the following order. In section 4.1, we present the number of voxels for which a significant association with FA was identified for each genetic variant and demographic feature. In Section 4.2, we summarize the results for the brain regions of interest (ROIs), defined by a well-established white matter atlas. We also provide results obtained from two-sided hierarchical clustering of the ROIs and genetic variants. In Section 4.3, we report the dominant magnitude and directions of the effect on FA alteration for significant genetic variants and demographic feature whithin each the ROI.

4.1 Genetic variants and clinical and demographic features associated with FA

Table 3 presents the resultant numbers of voxels for which statistically significant differential expression of mean FA was evident between the factor levels of each candidate genetic variant or clinical/demographic feature.

Table 3.

Number of significant voxel locations identified for each variable using iBANG analysis, sorted in decreasing order. Bayesian FDRs set to δ = 0.1 for each variable. The top (bottom) panel shows the genetic variants and demographic variables.

Genetic variants	Description	Number of significant voxels
GAD1a	glutamate decarboxylase 1 (brain, 67kDa)	5217
HTR2A	5-hydroxytryptamine (serotonin) receptor 2A, G protein-coupled	1413
TH	tyrosine hydroxylase	1332
GAD1b	glutamate decarboxylase 1 (brain, 67kDa)	1207
SLC6A4b	solute carrier family 6 (neurotransmitter transporter), member 4	1125
ADRA1A	adrenoceptor alpha 1A	1036
SLC6A3b	solute carrier family 6 (neurotransmitter transporter), member 3	1017
ADRA1D	adrenoceptor alpha 1D	813
HT2CR	5-hydroxytryptamine (serotonin) receptor 2C, G protein-coupled	805
COMT	catechol-O-methyltransferase	721
HT1A	tryptophan hydroxylase 1	688
CHRNA5	cholinergic receptor, nicotinic, alpha 5 (neuronal)	670
TPH1	tryptophan hydroxylase 1	666
SLC6A4a	solute carrier family 6 (neurotransmitter transporter), member 4	654
DRD2b	dopamine receptor D2	611
SLC6A3a	solute carrier family 6 (neurotransmitter transporter), member 3	476
DRD2a	dopamine receptor D2	439
DBH	dopamine beta-hydroxylase (dopamine beta-monooxygenase)	413
BDNF	brain-derived neurotrophic factor	392
TPH2	tryptophan hydroxylase 2	366
MAOB	monoamine oxidase B	359
Demographics
Cocaine abuse	Cocaine user=1 vs Control=0	3100
Age		1127
Gender		1086

Genetic variants associated with FA

Our study suggests that the impact of GAD1^a on diffusion in the white matter of the brain was extensive in comparison to the other 20 genetic variants. A total of 5217 voxel locations were found to be significantly associated with GAD1^a, nearly 4 times more than the second most influential genetic variant, HTR2A.

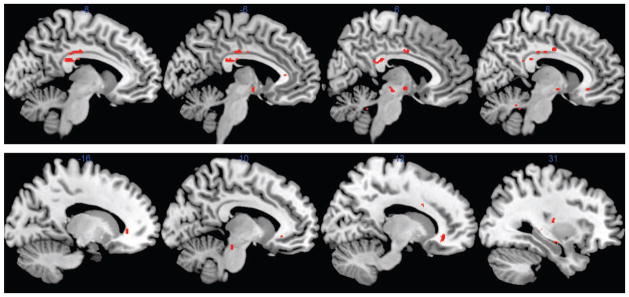
Figure 2 depicts the multi-slice sagittal views of the neuroanatomic locations of significant regions (SRs) in the white matter of the brain that were impacted by GAD1^a and GAD1^b respectively. In addition, 1207 voxels were identified as significant for GAD1^b. In Section S5 of supplementary materials, Figure S9 displays more anatomic locations of SRs for GAD1^a. Both GAD1^a and GAD1^b code for glutamic acid decarboxylase (GAD), a rate-limiting enzyme in synthesis of GABA in inhibitory interneurons. GABA is the major inhibitory neurotransmitter in the brain, GABAergic neurotransmission plays a critical role in drug-reward and drug- seeking behavior (Hyman and Malenka, 2001). Expression of the GAD1 gene is highly regulated by neuronal activity in the prefrontal cortex of the brain in cocaine users (Enoch et al., 2012). SRs were also evident in more than 1000 voxels for each of the following genetic variants: HTR2A, a 5-HT receptor subtype; and SLC6A4^b, a mediator of reuptake of 5-HT; TH involved in the synthesis of dopamine; SLC6A3^b, a mediator of reuptake of dopamine; and ADRA1A, a norepinephrine postsynaptic receptor. In Section S5 of supplementary materials, each row of Figure 10 displays the anatomic locations of SRs for one of these genetic variants.

Figure 2.

Multi-slice sagittal views displaying significant regions¹associated with GAD1^a and GAD1^b respectively from the top to the bottom panel. The SRs, depicted in red, characterize locations for which alteration of mean FA was evident from statistical analysis.

Clinical and demographic features associated with FA

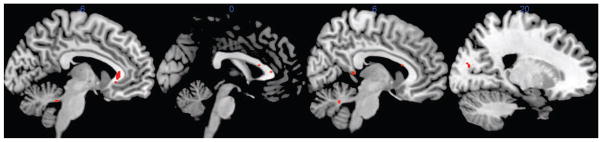
Diffusion in the white matter of the brain as measured by FA was significantly impacted by cocaine abuse to the extent of 3100 voxels. Figure 3 depicts the neuroanatomic regions for which significant differences in the mean FA were evident between cocaine users and healthy controls. In Section S5, Figure S11 of supplementary materials more anatomic locations of SRs for cocaine abuse is displayed. In addition, both demographic variables (age and gender) significantly impacted at least 1000 voxels.

Figure 3.

Multi-slice sagittal views displaying significant regions associated with cocaine consumption. The SRs, depicted in red, characterize locations for which alteration of the mean FA was evident from statistical analysis.

We evaluated the partial effects of cocaine consumption in the presence of the of other independent variables, consisting of gene variants and demographic features. Our study confirms previous studies that have found that numerous anatomical brain regions involved in the induction and long-term sensitization to cocaine are impacted by the consumption of the substance (Stein and Fuller, 1993; Hammer and Cooke, 1994; Hadfield, 1995). Several imaging studies have demonstrated that cocaine consumption leads to alterations in neuronal activity in the prefrontal cortex (Beyer and Steketee, 1999; Jentsch and Taylor, 1999; Vanderschuren and Kalivas, 2000).

4.2 Cluster analysis of ROIs, genetic variants, and clinical and demographic features

We further refined our inference using the white matter atlas developed by the Johns Hopkins University (JHU) (Wakana et al., 2004). The atlas enabled us to map the locations of significant voxels into the 48 white matter regions of interest (ROIs) detailed in Table 4.

Table 4.

Regions of white matter defined by the Johns Hopkins University atlas

ROI	Description
1	Middle cerebellar peduncle
2	Pontine crossing tract
3	Genu of corpus callosum
4	Body of corpus callosum
5	Splenium of corpus callosum
6	Fornix
7	Corticospinal tract R
8	Corticospinal tract L
9	Medial lemniscus R
10	Medial lemniscus L
11	Inferior cerebellar peduncle R
12	Inferior cerebellar peduncle L
13	Superior cerebellar peduncle R
14	Superior cerebellar peduncle L
15	Cerebral peduncle R
16	Cerebral peduncle L
17	Anterior limb of internal capsule R
18	Anterior limb of internal capsule L
19	Posterior limb of internal capsule R
20	Posterior limb of internal capsule L
21	Retrolenticular part of internal capsule R
22	Retrolenticular part of internal capsule L
23	Anterior corona radiate R
24	Anterior corona radiate L
25	Superior corona radiate R
26	Superior corona radiate L
27	Posterior corona radiate R
28	Posterior corona radiate L
29	Posterior thalamic radiation include optic radiation R
30	Posterior thalamic radiation include optic radiation L
31	Sagittal stratum include inferior longitudinal fasciculus and inferior fronto occipital fasciculus R
32	Sagittal stratum include inferior longitudinal fasciculus and inferior fronto occipital fasciculus L
33	External capsule R
34	External capsule L
35	Cingulum cingulated gyrus R
36	Cingulum cingulated gyrus L
37	Cingulum hippocampus R
38	Cingulum hippocampus L
39	Fornix cres Stria terminalis cannot be resolved with current resolution R
40	Fornix cres Stria terminalis cannot be resolved with current resolution L
41	Superior longitudinal fasciculus R
42	Superior longitudinal fasciculus L
43	Superior fronto occipital fasciculus could be a part of anterior internal capsule R
44	Superior fronto occipital fasciculus could be a part of anterior internal capsule L
45	Uncinate fasciculus R
46	Uncinate fasciculus L
47	Tapetum R
48	Tapetum L

Cluster analyses

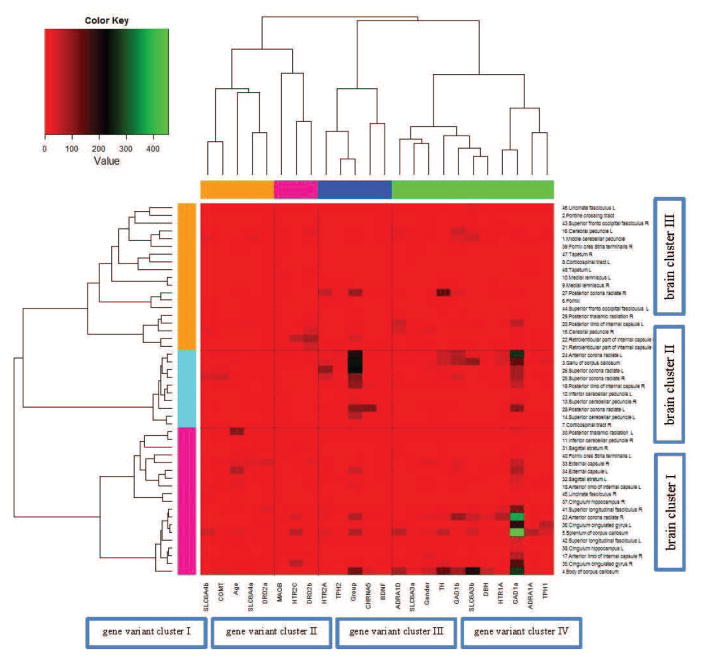
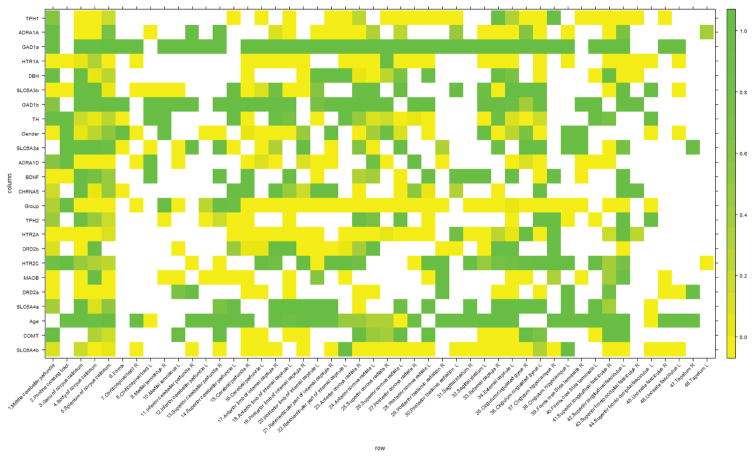
Two-sided hierarchical clustering of ROIs and genetic variants, and clinical/demographic features was implemented using counts of significant voxels obtained within each ROI as defined by the JHU atlas, with the aim of better understanding functional interdependencies among genes and regions of the brain. Ward’s method was used to minimize the total within-cluster variance (Szekely and Rizzo, 2005). Figure 4 presents the results of the cluster analysis, which resulted in four clusters among genetic-demographic features and three clusters of JHU ROIs. Table 5 reports cluster assignments among the white matter ROIs (top) and genetic variants (bottom). Genetic variants belonging to the same genes predominately clustered together, such as SLC6A4^b and SLC6A4^a in cluster one, and GAD1^a and GAD1^b in cluster three.

Figure 4.

Two-sided hierarchical clustering²of the neuroimaging-genetic findings based on the John Hopkins University white matter atlas. Green indicates an increased number of significant voxels for the ROI of the brain and genetic variant combination. The analysis resulted in four genetic variant clusters, denoted as genetic variant cluster I, genetic variant cluster II, genetic variant cluster III, and genetic variant cluster IV; and three clusters of brain ROIs defined by the JHU atlas, which are denoted as brain cluster I, brain cluster II, and brain cluster III. The individual cluster elements are tabulated in Table 5.

Table 5.

Two-sided hierarchical clustering of the neuroimaging-genetic data: the top panel lists the brain ROIs and the bottom panel lists the genetic variants in each cluster based on two-sided hierarchical clustering of the neuroimaging-genetic data in Figure 4.

Clusters of brain regions of interest based on two-sided hierarchical clustering of the neuroimaging-genetic data
brain cluster I	brain cluster II	brain cluster III
4.Body of corpus callosum	3.Genu of corpus callosum	1.Middle cerebellar peduncle
5.Splenium of corpus callosum	7.Corticospinal tract R	2.Pontine crossing tract
11.Inferior cerebellar peduncle R	12.Inferior cerebellar peduncle L	6.Fornix
17.Anterior limb of internal capsule R	13.Superior cerebellar peduncle R	8.Corticospinal tract L
18.Anterior limb of internal capsule L	14.Superior cerebellar peduncle L	9.Medial lemniscus R
23.Anterior corona radiate R	19.Posterior limb of internal capsule R	10.Medial lemniscus L
30.Posterior thalamic radiation L	24.Anterior corona radiate L	15.Cerebral peduncle R
31.Sagittal stratum R	25.Superior corona radiate R	16.Cerebral peduncle L
32.Sagittal stratum L	26.Superior corona radiate L	20.Posterior limb of internal capsule L
33.External capsule R	28.Posterior corona radiate L	21.Retrolenticular part of internal capsule R
34.External capsule L		22.Retrolenticular part of internal capsule L
35.Cingulum cingulated gyrus R		27.Posterior corona radiate R
36.Cingulum cingulated gyrus L		29.Posterior thalamic radiation R
37.Cingulum hippocampus R		39.Fornix cres Stria terminalis R
38.Cingulum hippocampus L		43.Superior fronto occipital fasciculus R
40.Fornix cres Stria terminalis L		44.Superior fronto occipital fasciculus L
41.Superior longitudinal fasciculus R		46.Uncinate fasciculus L
42.Superior longitudinal fasciculus L		47.Tapetum R
45.Uncinate fasciculus R		48.Tapetum L
Genetic variants clusters based on two-sided hierarchical clustering of the neuroimaging-genetic data
genetic variant cluster I	genetic variant cluster II	genetic variant cluster III	genetic variant cluster IV
DRD2a	MAOB	HTR2A	ADRA1D
COMT	HTR2C	TPH2	SLC6A3a
SLC6A4b	DRD2b	BDNF	TPH1
SLC6A4a		CHRNA5	TH
			GAD1b
			SLC6A3b
			DBH
			HTR1A
			GAD1a
			ADRA1A

4.3 Magnitude and direction of FA alteration in ROIs

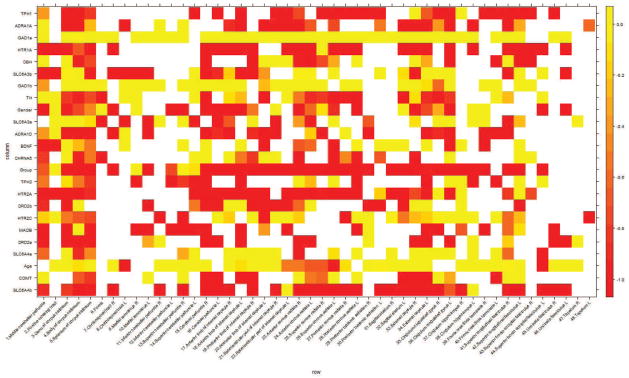
Figures 5 and 6 depict the extent and nature of FA alterations among the candidate genetic variants and clinical and demographic features considered within each ROI of the JHU white matter atlas. In Figure 5, we plot the proportion of significant voxels with positive regression coefficients. Green represents FA enhancement; yellow characterizes the absence of FA enhancement. In Figure 6, red depicts the proportion of voxels with negative regression coefficients, suggesting that these features are predominately associated with FA attenuation. In both Figures, white represents the absence of significant voxels in that particular brain region-by-feature combination. Figure 5 suggests that both GAD1^a and GAD1^b are associated with FA enhancement in most regions defined by the JHU white matter atlas; whereas Figure 6 demonstrates an association with FA diminishment in cocaine users.

Figure 5.

The magnitude of FA enhancement as measured by the proportion of significant voxels with positive regression coefficients. The color key represents the extent of FA alteration. Green indicates the highest enhancement; yellow indicates no enhancement of FA value. White indicates absence of significant voxels for the specific combination of brain ROIs or genetic variants and demographic feature.

Figure 6.

The magnitude of FA diminishment as measured by the proportion of significant voxels with negative regression coefficients. The color key represents the extent of FA alteration. Red indicates the highest diminishment; yellow indicates no diminishment of FA value. White indicates absence of significant voxels for the specific combination of brain ROIs and genetic variants or demographic feature.

4.4 Comparison of Bayesian model averaging versus full model

We also compared our Bayesian model averaging (BMA) based inference to a full Bayesian model (Full) fit with no model averaging – to determine the necessities/gains of accounting the uncertainty inherent in the model selection process. To this end, we undertook several, more formal comparisons to describe the extent of relative differences between BMA and Full model inferences on the basis of several metrics such as goodness-of-fit measures, predictive performance, significant voxels, and point estimation of the regression coefficients.

Specifically, we compared BMA and Full model inference using two goodness-of-fit metrics: (i) approximate Deviance information criterion (aDIC), and (ii) Bayesian information criterion (BIC), which are indicative of the (relative) fit of our models to the observed data. Using both metrics we found that the BMA-based methods consistently outperformed the full model (see Section S2 of the supplementary materials for more details). We further evaluated the predictive performance of our models using log predictive scores (LPS). We evaluated the predictive performance of LPS considering four different test-training scenarios by splitting the sample to test and train sets of {33%, 25%, 20%, 10%}. In all scenarios, the BMA-based LPS scores are lower than the Full model, thus indicating better predictive performance (see Section S3 of the the supplementary materials for more details). Finally, we compared the regression coefficient estimates of BMA and Full model the entire white matter of the brain for significant factors: cocaine abuse, GAD1^a, and GAD1^b. Results depicted the disadvantage of using full Bayesian model since the range of coefficients were very narrow with most of the values close to zero. As a result BMA detects much larger number of significant voxels as compared to full model, which we conjecture is due to this over-shrinkage of the estimates (see Section S4 of the the supplementary materials for more details.)

5 Discussion

This article presents iBANG, a general method for the integrative Bayesian analysis of voxel-wise neuroimaging and genetic data. The key features of our modeling strategy are to allow for the quantification of model uncertainty via Bayesian model averaging, account for spatial correlation via local smoothing, and explicitly control for multiplicity via Bayesian false discovery rate procedures. In addition, by decoupling the model fitting and inference, we are able to scale our methods to conduct voxel-wise analyses of the entire white matter of the brain with multiple genetic variables. Although our methods are motivated by a specific neuroimaging-genetic study in cocaine addiction –our methods are general and applicable to any voxel-wise imaging modality.

We exemplify our methods using neuroimaging-genetic data from a cocaine addiction study. We analyze the integrity of the white matter of the brain and demonstrate the possible effect of candidate genetic variants and demographic factors on white matter impairment in users of cocaine. Results of this analysis showed that gene polymorphisms associated with the synthesis of GABA, serotonin, and dopamine and the function of the corresponding receptors were associated with brain FA in cocaine-dependent subjects. At least some previous preclinical and clinical studies have found a relationship between cocaine use and GAD1. A study by (Enoch et al., 2012) showed that GAD1 and GAD2 expression levels in postmortem brains were related to cocaine use. In addition, our findings of reduced white matter FA in cocaine users are consistent with previous studies (Beyer and Steketee, 1999; Jentsch and Taylor, 1999; Vanderschuren and Kalivas, 2000; Lim et al., 2002; Moeller et al., 2005). However, our methods showed evidence of FA diminishment in most brain regions of interest, which is an interesting finding that is worthy of further investigation.

To identify significant regions of the brain associated with genetic variables, we applied voxel-wise FDR correction to the smoothed posterior probability maps (sPPMs) for each genetic covariate of interest, independently. Another alternate and interesting approach, as pointed out by one of the reviewers, is to use the notion of a “topological FDR” (Chumbley and Friston, 2009) wherein topological boundaries of activation are identified around local inflection points i.e. a priori clustering of voxels (e.g via spatial volumes) into discrete sets and treated as the units of inference. As argued by the authors, this topological perspective refines the interpretation as well as inference, and allows for more rigorous control of a smaller multiple comparison problem. In a classical (frequentist) and single covariate (one treatment) settings, the authors propose an approach that combines the FDR procedure on p-values obtained from SPM with Random Field Theory (RFT) to find regional (defined by topological property) activation of the underlying signal. We take a different tack in this article. From a Bayesian viewpoint, the sPPMs inherently account for the spatial structure in the data (as opposed to raw PPMs) and thus define contiguous region of activation. Our main motivation for doing this is to allow our methods to scale to large datasets as well as provide principled statistical inference while accounting for various sources of variability induced by model selection and spatial heterogeneity. Extending our FDR approach to a more global topological level, while no doubt interesting, is a non-trivial one, for the following reasons: (i) the approach must accommodate two hierarchical levels of multiplicity – within and across genetic covariate maps; (ii) requires prior null and alternative hypotheses specifications at each level and (iii) in a DTI context, this would also require a more precise definition of a topological feature. We leave these tasks for future consideration.

There are several possible extensions and generalizations of our iBANG models to more general settings. In this work, we considered full MCMC-based posterior sampling approaches to estimate the exact model probabilities for each (genetic) covariate at each voxel location. Another approximate approach based on Savage-Dickey Bayes factors has been recently proposed by (Rosa et al., 2012). In their approach, first the largest (full) model is computed and subsequently, a post-hoc approach is used to calculate the model evidence for any (reduced) submodel by using a generalization of the Savage-Dickey density ratio (Dickey, 1971). The benefit of this approach is a reduction in computational time, since a potentially huge space of the nested sub-models can be explored using single model fit.

Another natural advancement is to incorporate spatial correlation in the Bayesian model averaging in the first step of the model fitting. We eschew this step because of computational constraints and so avoid evaluating and storing large covariance matrices. However, the use of lower dimensional projections of these matrices, such as principal component analysis (PCA) or independent component analysis (ICA) could potentially circumvent these issues. Our implementation is currently limited to one imaging parameter (FA, in this case). In future extensions, one could simultaneously consider multiple imaging parameters, such as mean diffusivity, axial diffusivity, and radial diffusivity. We leave these tasks for future work.

Highlights.

• Statistical framework for integrative Bayesian analysis of neuroimaging-genetic data.

• Delineate significant brain regions associated with genetic variants.

• Fast computational schemes scalable to voxel-wise model fitting and inference.

• Cocaine consumption is associated with fractional anisotropy (FA) reduction.

• Gene polymorphisms associated with GABAergic were associated with FA.