Unifying dynamical and structural stability of equilibria

Abstract

We exhibit a fundamental relationship between measures of dynamical and structural stability of linear dynamical systems—e.g. linearized models in the vicinity of equilibria. We show that dynamical stability, quantified via the response to external perturbations (i.e. perturbation of dynamical variables), coincides with the minimal internal perturbation (i.e. perturbations of interactions between variables) able to render the system unstable. First, by reformulating a result of control theory, we explain that harmonic external perturbations reflect the spectral sensitivity of the Jacobian matrix at the equilibrium, with respect to constant changes of its coefficients. However, for this equivalence to hold, imaginary changes of the Jacobian’s coefficients have to be allowed. The connection with dynamical stability is thus lost for real dynamical systems. We show that this issue can be avoided, thus recovering the fundamental link between dynamical and structural stability, by considering stochastic noise as external and internal perturbations. More precisely, we demonstrate that a linear system’s response to white-noise perturbations directly reflects the intensity of internal white-noise disturbance that it can accommodate before becoming stochastically unstable.

1. Prologue

Understanding the stability of dynamical systems is fundamental in numerous applications, from classical mechanics, fluid dynamics, engineering, to biology [1–6]. Stability refers to the ability of a subset of phase space to attract trajectories from its vicinity. In other words, a given state is dynamically stable if trajectories remain close to that state despite small perturbations. Such sets are called attractors, the most basic kind being equilibria. Regardless of their conceptual simplicity, they commonly appear in a large variety of models. For instance, their study in ecology is fundamental to understand the mechanisms that stabilize ecosystems and support their staggering diversity [6]. In fluid mechanics, the laminar state can be seen as an equilibrium, and the transition to turbulence as caused by a loss of stability [1]. In the context of dynamics of nodes of electric power grids, the equilibrium is a desired state where the generator operates in synchrony with the grid [4].

In deterministic dynamical systems, vanishing points of the generating vector field are (if they exist) the system’s equilibria. Dynamical stability of a given equilibrium is assessed in terms of the spectrum of the associated Jacobian matrix. The stability criterion is that all its eigenvalues have negative real parts. Since Lyapunov [7], this approach has been fruitfully applied across disciplines [6,8,9].

On the other hand, structural stability relates to the robustness of the qualitative dynamical picture with respect to small changes in the system structure [10,11]. This notion is particularly important when the system is a simplified model of a more complicated real-world system, which is virtually always the case in applications. For the model to inform on the real-world system, it must be robust with respect to small perturbations, uncertainties and so forth [12,13]. There are broad classes of models that are known to be structurally stable, the most basic ones being hyperbolic linear systems, a result that justifies the study of linearized models in the vicinity of equilibria.

The above-described two stability notions are qualitative, yet it is often important to quantify stability, either dynamical or structural, in order to compare different models or to assess the effect of parameters on stability. Qualitative notions answer the question is a particular state (or model) stable? Whereas quantitative measures answer how stable is this state (or model)? Dynamical stability is typically quantified via the system response to pulse-perturbations, that is, instantaneous displacements in phase space, but other perturbations are also important. For instance, periodic forcing can reveal resonances. Although far less common in the literature [14–16], measures of structural stability are by no means less relevant. They quantify the stability of the model itself, that is, the intensity of structural perturbations that it can accommodate before its behaviour qualitatively changes.

In this article, we focus on real, stable, linear dynamical systems, typically derived from a linearization of an underlying nonlinear model in the vicinity of a stable equilibrium. We do not address the issue of finding the equilibrium, but rather assume that an equilibrium exists and is fixed, and that the local dynamics in its vicinity are known. As long as we remain in a neighbourhood of the equilibrium, our analysis does not depend on the details of the underlying nonlinear model.

In this linear (or local) setting, we introduce natural measures of dynamical stability, quantifying a system’s response to persistent forcing. We compare them with natural measures of structural stability, quantifying the smallest change in the dynamical structure (i.e. of the interactions between variables) leading to destabilization. We show that these measures coincide, so that, in the vicinity of an equilibrium, the dynamical response to external perturbations reflects the system’s sensitivity to changes of its local structure.

In §2, we revisit a result of control theory, showing that responses to harmonic external perturbations reflect the spectral sensitivity of the Jacobian matrix at the equilibrium, with respect to constant changes of its coefficients. In an elementary example, we illustrate a caveat of this approach, showing that this relationship does not always hold for real systems.

In §3, in which our main result is stated, we demonstrate that the fundamental link between dynamical and structural stability of linear systems can be recovered by considering stochastic noise as external and internal perturbations.

2. Dynamical and structural stability: harmonic perturbations

The standard procedure to assess stability of an equilibrium consists of linearizing the vector field in its vicinity, effectively reducing the local dynamics to a linear system of the form $\dot{\mathit{\text{ x}}}=A\mathit{\text{ x}}$, where A is the Jacobian matrix evaluated at the equilibrium, and the vector x denotes multidimensional displacements from that equilibrium. Defining the spectral abscissa of A as

$$\alpha (A)=sup\{\mathrm{\Re }(\mathrm{\lambda })\hspace{0.17em}|\hspace{0.17em}\mathrm{\lambda }\in \text{spect}(A)\},$$ 2.1

we say that a matrix with negative spectral abscissa is stable (i.e. the associated equilibrium x=0 is stable) and unstable otherwise.

A straightforward way to quantify the dynamical stability of a stable equilibrium is to analyse the system’s local response to harmonic forcing. This amounts to solving

$$\dot{\mathit{\text{x}}}=A\mathit{\text{x}}+\mathrm{\Re }({\mathrm{e}}^{\mathrm{i}\omega t}\mathit{\text{u}}),$$

where $\omega \in \mathbb{R}$ is the frequency of a real rotating perturbation. The stationary response is ℜ(e^iωtw) with w=(iω−A)⁻¹u. The norm of the complex vector w is the mean amplitude of the induced oscillations. The spectral norm of the matrix (iω−A)⁻¹ gives the strongest system response to harmonic forcing of frequency ω. To define a measure of stability, we take the inverse of the largest system amplification of harmonic forcing. This translates as

$${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}(A)=1/\underset{\omega \in \mathbb{R}}{sup}\parallel {(\mathrm{i}\omega -A)}^{-1}\parallel .$$ 2.2

The number ω realizing the maximum is called the resonant frequency. It can be shown [17] that ${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}$ relates to the maximal power gain over wide-sense stationary signals, indicating that, although defined with respect to a specific class of forcing, it is a general indicator of the ability of an equilibrium to absorb external perturbations.

Let us now turn to the problem of quantifying structural stability. For equilibria, we may consider how close the Jacobian matrix A is from being unstable, that is, the minimal constant change in its coefficients that can push its dominant eigenvalue into the instability region $\{z\in \mathbb{C}\hspace{0.17em}|\hspace{0.17em}\mathrm{\Re }(z)\ge 0\}$ of the complex plane. Measuring the distance to instability as the spectral norm of the smallest matrix P rendering A+P unstable, this yields

$${\mathcal{S}}_{\mathrm{STR}}^c(A)=inf\{\parallel P\parallel \hspace{0.17em}|\hspace{0.17em}\alpha (A+P)>0\}\le |\alpha (A)|\}.$$ 2.3

This definition of structural stability is also known as the stability radius [18]. The inequality in (2.3) comes from the fact that the perturbation $P=-\alpha (A)\mathbb{I}$ is always sufficient to destabilize A. In fact, it is the most efficient way to destabilize A when A is normal (i.e. has orthonormal eigenvectors) in that case the inequality is an equality [8]. The absolute value of the spectral abscissa |α(A)| is the Euclidian distance to instability measured in the complex plane. Hence, the two distances, stability radius and spectral abscissa, coincide when the Jacobian matrix is normal.

There is a strong link between ${\mathcal{S}}_{\mathrm{STR}}^c$ and the dynamical measure ${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}$ introduced in (2.2). To reveal this link suppose that for some stable matrix A, ${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}(A)=1/v,$ where v>0 is the strongest response associated with the resonance ω. Pick two normalized vectors: u, spanning the direction of perturbation and w, spanning the direction of response, both associated with the resonance ω. We have that

$${(\mathrm{i}\omega -A)}^{-1}\mathit{\text{u}}=v\mathit{\text{w}}\hspace{0.17em}\iff \hspace{0.17em}A\mathit{\text{w}}+v^{-1}\mathit{\text{u}}=\mathrm{i}\omega \mathit{\text{w}}.$$

We can construct a destabilizing matrix from the vectors u and w. This is done by choosing P=v⁻¹uw*, so that ∥P∥=v⁻¹, Pw=v⁻¹u and

$$(A+P)\mathit{\text{w}}=\mathrm{i}\omega \mathit{\text{w}}\hspace{0.17em}\Rightarrow \hspace{0.17em}\alpha (A+P)\ge 0.$$

Hence, P destabilizes A, meaning that ${\mathcal{S}}_{\mathrm{STR}}^c(A)\le \parallel P\parallel =v^{-1}={\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}(A)$.

Conversely, suppose that ${\mathcal{S}}_{\mathrm{STR}}^c(A)=p$. There exists a matrix P with ∥P∥=p such that A+P is unstable: for some ω and normalized vector w,

$$(A+P)\mathit{\text{w}}=\mathrm{i}\omega \mathit{\text{w}}\hspace{0.17em}\iff \hspace{0.17em}\mathit{\text{w}}={(\mathrm{i}\omega -A)}^{-1}\mathit{\text{u}},$$

with u=Pw. Because ∥u∥≤p, we deduce that ∥(iω−A)⁻¹∥≥p⁻¹. Hence,

$${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}={\mathcal{S}}_{\mathrm{STR}}^c$$ 2.4

giving from (2.2) a computable expression for structural stability. Equation (2.4) corresponds to a well-known result in control theory [18], which we interpret here in terms of dynamical and structural stability of equilibria.

There is however a caveat. The quantitative measure of structural stability we have considered allows for complex matrix perturbations, that almost never make sense in applications. In fact, computing the corresponding real structural stability, which we denote as ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}$, involves a complicated global optimization problem [19]. In general, dynamical stability can be much smaller than its real structural counterpart. This issue is particularly apparent in the following elementary example. Consider the sequence of Jacobian matrices

$$A=\left(\begin{array}{cc}-1& M^2\\ -1& -1\end{array}\right)\text{with}\hspace{0.17em}M=1,2,\dots ,$$ 2.5

whose eigenvalues are −1±iM, so that α(A)=−1. The associated equilibria are stable for all values of M. The strongest response to harmonic forcing grows with M. In addition, complex perturbations have an effect of order M on the real part of the spectrum, so that perturbations of order M⁻¹ can destabilize the matrix.

This is not true for real perturbations as

$$1={\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}(A)>{\mathcal{S}}_{\mathrm{STR}}^c(A)={\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}(A){\to }_{M\to \mathrm{\infty }}0.$$

Real structural stability can thus be completely disconnected from its dynamical counterpart.

3. Dynamical and structural stability: white-noise perturbations

Let us now transpose the relationship between dynamical and structural stability to white-noise forcing, often used to model the effect of erratic external perturbations [17,20]. The local effect of white noise is best expressed using the formalism of stochastic differential equations (SDEs). It reads as

$$\mathrm{d}{\mathit{\text{X}}}_t=A{\mathit{\text{X}}}_t\hspace{0.17em}\mathrm{d}t+T\hspace{0.17em}\mathrm{d}{\mathit{\text{W}}}_t,$$ 3.1

where W_t is a vector of independent Wiener processes, representing various external factors acting on the system, with the matrix T describing how these factors affect system variables. The first moments ${\mathit{\mu }}_t=\mathbb{E}{\mathit{\text{ X}}}_t$ evolve as ${\dot{\mathit{\mu }}}_t=A{\mathit{\mu }}_t$ and converge to zero if A is stable. The second moments, represented as covariance matrices $C_t=\mathbb{E}{\mathit{\text{ X}}}_t{\mathit{\text{ X}}}_t^{\mathrm{\top }}$, follow the deterministic equation [21,22]

$${\dot{C}}_t=\hat{A}{C}_t+\mathrm{\Sigma },$$ 3.2

with $\hat{A}C=AC+C{A}^{\mathrm{\top }}$, called hereafter the lifted operator, and Σ=TT^⊤, a positive semi-definite matrix, encoding the effective correlations of the noise. If A is stable, any initial covariance matrix converges to

$$\mathit{\Pi }=-{\hat{A}}^{-1}\mathrm{\Sigma },$$

the unique attractor of (3.2).

In analogy with the measure ${\mathcal{S}}_{\mathrm{DYN}}^{\mathfrak{h}}$ constructed via the largest local response to normalized harmonic perturbations, we define a measure of dynamical stability by taking the inverse of the strongest system response over normalized white-noise perturbations. This leads us to

$${\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A)=1/\underset{\mathrm{\Sigma }\ge 0,\hspace{0.17em}\parallel \mathrm{\Sigma }{\parallel }_{\mathrm{F}}=1}{sup}\parallel {\hat{A}}^{-1}\mathrm{\Sigma }{\parallel }_{\mathrm{F}},$$ 3.3

where the supremum is taken over covariance matrices of the real external noise. The use of the Frobenius norm, ∥Σ∥_F=Tr(Σ^⊤Σ)^1/2, to normalize the correlation matrices allows us to see them as vectors endowed with the usual scalar product and Euclidean norm. Because $-{\hat{A}}^{-1}$ is a completely positive map, the matrix Σ realizing the norm $\parallel {\hat{A}}^{-1}\mathrm{\Sigma }{\parallel }_{\mathrm{F}}=\parallel {\hat{A}}^{-1}\parallel$ is a positive semi-definite matrix [23]. We thus get that

$${\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A)=\frac{1}{\parallel {\hat{A}}^{-1}\parallel }.$$ 3.4

Note that the lifted operator $\hat{A}$ can be expressed as a larger matrix $A\otimes \mathbb{I}+\mathbb{I}\otimes A$, giving a simple way to compute ${\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}$.

So far, as in control theory, we considered constant changes in the Jacobian matrix to quantify structural stability. We now embark on a different path, assuming that the coefficients of the Jacobian matrix fluctuate. In time-series analysis, such variations are called process errors, whereas those previously considered would correspond to observation errors [24]. To model the effect of internal perturbations, we pick a set of real matrices P_k and independent Wiener processes $W_t^k$, and consider the following homogeneous linear SDE

$$\mathrm{d}{\mathit{\text{X}}}_t=(A\hspace{0.17em}\mathrm{d}t+\sum _k{P}_k\hspace{0.17em}\mathrm{d}{W}_t^k){\mathit{\text{X}}}_t,$$ 3.5

where the matrices P_k describe fluctuations of the matrix entries A_ij and their correlations. For example, independent fluctuations of variance σ² of all entries A_ij would correspond to $P_k=\sigma {\mathit{\text{ e}}}_i{\mathit{\text{ e}}}_j^{\mathrm{\top }}$, where {e_i} stands for the standard orthonormal basis of phase space. Note that the representation of multiplicative noise in (3.5) corresponds to Itô’s interpretation of stochasticity [22]. We discuss this point further below. In Itô’s interpretation, the first moments μ are unperturbed, and follow ${\dot{\mathit{\mu }}}_t=A{\mathit{\mu }}_t$, converging to equilibrium if A is stable. The effect of allowing the interactions to fluctuate appears in the second moments—the (co)variances. To see this, we again lift the SDE (3.5) to act on covariance matrices, giving [21,22]

$$\dot{C_t}=(\hat{A}+\mathcal{P})C_t,$$ 3.6

with $\mathcal{P}(C)=\sum _k{P}_{k}C{P}_k^{\mathrm{\top }}$. Let us measure the intensity of the internal perturbation by the spectral norm $\parallel \mathcal{P}\parallel$. In the case of independent fluctuations of all entries of A, $\parallel \mathcal{P}\parallel =n^2{\sigma }^2$, with n the system dimension. We can then define stochastic structural stability as the minimal internal perturbation intensity able to destabilize the second moments of (3.5),

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)=inf\{\parallel \mathcal{P}\parallel \hspace{0.17em}|\hspace{0.17em}\alpha (\hat{A}+\mathcal{P})>0\},$$ 3.7

where the infimum is over perturbations $\mathcal{P}$ constructed from an arbitrary sequence of real matrices P_k.

Theorem 3.1 —

For real linear systems, measures of structural and dynamical stability coincide, in the sense that

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}={\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}.$$ 3.8

Dynamical stability is quantified as the inverse of the maximal variance amplification of external white-noise perturbation. Structural stability is quantified as the minimal internal white-noise perturbation needed to destabilize the system’s variance. It relates to ${\mathcal{S}}_{\mathrm{STR}}^c$ (resp. ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}$) the minimal complex (resp. real) constant perturbation able to destabilize the equilibrium’s Jacobian matrix, via the following chain of inequalities

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}\le 2{\mathcal{S}}_{\mathrm{STR}}^c\le 2{\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}\le 2|\alpha |$$ 3.9

with α the spectral abscissa of the Jacobian matrix at the equilibrium. (3.9) collapses onto an equality when the Jacobian is normal (i.e. has orthogonal eigenvectors).

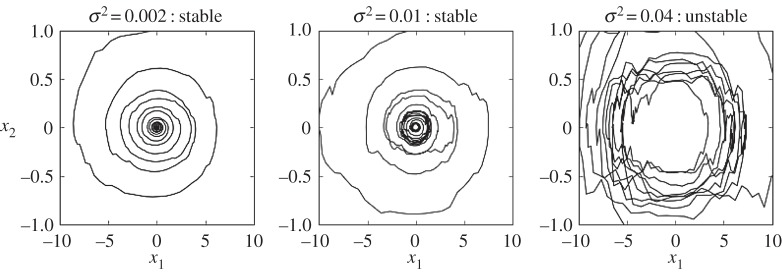
The example of Jacobian matrices (2.5) is revisited in figure 1. We see that the low stability with respect to constant imaginary perturbations detected by ${\mathcal{S}}_{\mathrm{STR}}^c$ is also present when considering real stochastic fluctuations in the matrix coefficients, as predicted by ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}$. Inequality (3.9) is illustrated in figure 2 showing that, although associated with real perturbations, ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}$ can sometimes be much smaller than its deterministic and complex counterpart ${\mathcal{S}}_{\mathrm{STR}}^c$.

Figure 1.

Stochastic destabilization by internal white-noise perturbation. The Jacobian matrix is $A=\left(\begin{array}{cc}-1& 100\\ -1& -1\end{array}\right)$. We have that $1/\parallel {\hat{A}}^{-1}\parallel \simeq 0.04$, so that according to (3.8) fluctuations $\mathcal{P}$ with intensity $\parallel \mathcal{P}\parallel \ge 0.04$ affecting the matrix A can destabilize the equilibrium. We show a realization of the process dX_t=(A dt+σP dW_t)X_t with $P=\left(\begin{array}{cc}-0.07& -0.27\\ -0.92& 0.37\end{array}\right)$ and ∥P∥=1. In the rightmost panel, the variance σ²=0.04 is large enough to show premises of destabilization. Recall that for this matrix the real stability radius was independent of M, with ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}(A)=1$.

Figure 2.

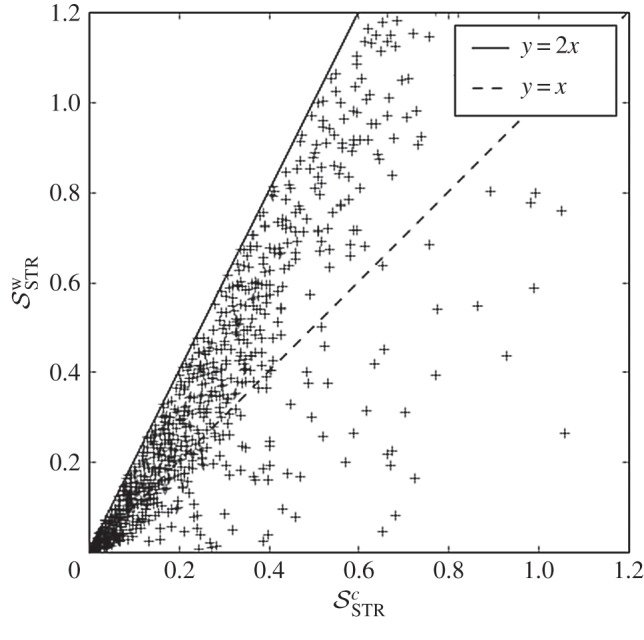
Illustration of the structural stability ordering (3.9). We randomly generated 1000 stable 3×3 matrices. Entries were independently drawn from a normal distribution of zero mean and unit variance, discarding unstable matrices. We see that the stochastic structural stability of a matrix, ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}$, can be much smaller than the smallest constant complex change needed to destabilize that matrix, ${\mathcal{S}}_{\mathrm{STR}}^c$. The equality ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}=2{\mathcal{S}}_{\mathrm{STR}}^c$ is attained for normal matrices.

We measured structural stability as a distance to instability from the perspective of the second moments of the linear SDE (3.5), yet any perturbation acting as a multiplicative noise can destabilize moments of high enough order.¹ However, as long as the second moments are bounded, Chebyshev’s inequality, that plays a pivotal role in the theory of persistence [25], provides a control on the probability of excursions away from equilibrium. Indeed, we have that $\parallel C_t{\parallel }_{\mathrm{Tr}}=\mathbb{E}\parallel {\mathit{\text{ X}}}_t{\parallel }^2$ and Chebyshev’s inequality reads, for any δ>0, and time t≥0,

$$\mathbb{P}(\parallel {\mathit{\text{X}}}_t\parallel \ge \delta )\le \frac{1}{{\delta }^2}\parallel C_t{\parallel }_{\mathrm{Tr}}$$ 3.10

which, by virtue of (3.6) and equivalence of trace and Frobenius norms, goes to zero as time flows forward as long as $\hat{A}+\mathcal{P}$ is stable. In other words, loosing stability in the sense of (3.7) implies loosing control on the probability of excursions from equilibrium. The importance of this kind of probabilistic stability, called mean-square asymptotic stability, is discussed in [20], with examples from ecology, turbulent fluid mechanics, and system control.

We mentioned that the dynamics defined by the SDE (3.5) correspond to Itô’s interpretation of Wiener processes [22]. Such stochastic signals can be seen as trains of delta peaks, occurring at random instants [22]. In Itô’s prescription, the intensity of random pulses should be determined by the state variables before the pulse. For instance, the pulse x(t)δ(t−t_k) arriving at time t_k should be multiplied by $x(t_k^{-})$. On the other hand, Statonovich’s prescription would be to multiply that pulse by $(x(t_k^{+})+x(t_k^{-}))/2$. The two prescriptions yield the same SDE when the noise is additive (i.e. only adds noise to dynamical variables), hence in our case, the same definition of dynamical stability ${\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}$. A difference occurs, the spurious drift, when the noise affects the intercations between dynamical variables, i.e. when it affects the Jacobian matrix as in (3.5). This yields a different definition of stochastic structural stability than ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}$. Choosing between the two prescriptions depends on the physical origin of the noise [22,26]. If the system is intrinsically stochastic, then Itô’s interpretation should be used. If the noise is created by the application of a random force on an otherwise deterministic system, then Stratonovich’s interpretation makes more sense.

4. Proving the theorem

To prove our main result, we follow a reasoning similar to the one that led to the identity (2.4). Beyond establishing the validity of our claim, the proof shows how to explicitly construct destabilizing internal perturbation from external perturbations. A construction that could be useful for applications.

Let us start by showing that ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}\le {\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}$. For a stable Jacobian matrix A, suppose that ${\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A)=1/v$. By (3.3), this means that there exists two positive normalized matrices, the noise correlation matrix Σ and the associated system response correlation matrix Π, such that

$$-{\hat{A}}^{-1}\mathrm{\Sigma }=v\mathit{\Pi }\hspace{0.17em}\iff \hspace{0.17em}\hat{A}\mathit{\Pi }+v^{-1}\mathrm{\Sigma }=0.$$

As in the deterministic setting, using Σ and Π, we construct a destabilizing operator $\mathcal{P}$. However, for this operator to represent real internal noise, it must be of the form $\sum _k{P}_k\cdot P_k^{\mathrm{\top }}$ for a set of real matrices P_k. To construct such an operator, we use the spectral decomposition of the positive semi-definite matrices Σ and Π

$$\mathrm{\Sigma }=\sum _{i=1}^n{\mathrm{\lambda }}_i{\mathit{\text{u}}}_i{\mathit{\text{u}}}_i^{\mathrm{\top }}\text{and}\mathit{\Pi }=\sum _{i=1}^n{\mu }_i{\mathit{\text{v}}}_i{\mathit{\text{v}}}_i^{\mathrm{\top }},$$

and put $P_k=\sqrt{{\mathrm{\lambda }}_i{\mu }_j/v}{\mathit{\text{ u}}}_i{\mathit{\text{ v}}}_j^{\mathrm{\top }}$, representing n² independent internal perturbations of the matrix A. We have

$$\begin{array}{rl}\mathcal{P}(C)& =\sum _k{P}_{k}C{P}_k^{\mathrm{\top }}\\ & =v^{-1}\sum _{i=1}^n{\mathrm{\lambda }}_i{\mathit{\text{u}}}_i{\mathit{\text{u}}}_i^{\mathrm{\top }}\sum _{j=1}^n{\mu }_j⟨{\mathit{\text{v}}}_j,C{\mathit{\text{v}}}_j⟩\\ & =v^{-1}\hspace{0.17em}\text{Tr}(\mathit{\Pi }C)\mathrm{\Sigma },\end{array}$$

and, using the Hilbert–Schmidt inner product 〈X,Y 〉=Tr(X*Y) from which the Frobenius norm derives, we see that $\mathcal{P}$ takes the compact form

$$\mathcal{P}=v^{-1}⟨\mathit{\Pi },\hspace{0.17em}\cdot \hspace{0.17em}⟩\mathrm{\Sigma },$$

showing that $\mathcal{P}(\mathit{\Pi })=v^{-1}\mathrm{\Sigma }$ and $\parallel \mathcal{P}\parallel =v^{-1}$. We thus have that

$$(\hat{A}+\mathcal{P})\mathit{\Pi }\ge 0.$$

Hence, $\mathcal{P}$ destabilizes the lifted dynamics and corresponds to real internal noise of intensity $\parallel \mathcal{P}\parallel =v^{-1}$. Thus,

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)\le {\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A).$$

Conversely, suppose that ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)=p$. There exists an operator $\mathcal{P}$ with $\parallel \mathcal{P}\parallel =p$ such that $\hat{A}+\mathcal{P}$ is unstable, i.e. it has a dominant eigenvalue on the imaginary axis. There can be strictly imaginary dominant eigenvalues, but we show in appendix A that there is also a dominant eigenvalue at zero. Hence, for some matrix X with ∥X∥_F=1

$$(\hat{A}+\mathcal{P})X=0\hspace{0.17em}\iff \hspace{0.17em}X=-{\hat{A}}^{-1}(Y),$$

with $Y=\mathcal{P}(X)$. Because ∥Y ∥_F≤p, we find that $\parallel {\hat{A}}^{-1}\parallel \ge p$, so that by virtue of (3.4)

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)\ge {\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A),$$

which concludes the proof of (3.8). We refer to appendix B for the proof of (3.9).

5. Epilogue

For linear systems, we demonstrated that dynamical and structural stability are remarkably connected concepts, in the sense that the dynamical response to erratic and persistent external perturbations (i.e. direct perturbations of dynamical variables) exactly reflects a system’s sensitivity to stochastic fluctuations of its internal structure (i.e. of the interactions between its constituent variables). This means that, in the vicinity of an equilibrium, the dynamical response to external perturbations informs on the system’s sensitivity to changes of its local structure.

We quantified dynamical stability via the maximal system response to external perturbations, and structural stability via the minimal destabilizing internal perturbation. However, it is not necessary to consider these worst-case scenarios for a connection between these two stability notions to hold. Indeed, to any external perturbation and associated system response, there corresponds a destabilizing internal perturbation. The larger the amplification of the external perturbation, the smaller the intensity of the corresponding destabilizing internal perturbation.

To derive our main result, we used Itô’s interpretation of Wiener processes [22], as opposed to the one of Stratonovich. We explained that they are equivalent when the noise is external but differ when the noise affects the interactions between variables. This would yield a potentially different definition of stochastic structural stability then the one for which our theorem holds. We leave it as an open problem to transpose the relationship between dynamical and structural stability under Stratonovich’s interpretation.

Beyond this technical issue, it has long been acknowledged that local stability analysis is not sufficient to fully grasp the stability of attractors. Outside the linear framework, other stability questions can and must be raised. For instance, the size of basins of attraction can be a fundamental global feature, independent of local stability [27,28]. In models of interacting species, other notions of structural stability have been introduced, based on the feasibility of an equilibrium taking strictly positive values [14–16]. In a nonlinear setting, our stability measures have to be interpreted with care. Indeed, they reflect the effect of local perturbations, which might differ from those induced by directly perturbing parameters of the underlying nonlinear model. How changes in parameters affect the local dynamics depends on the exact form of the vector field.

Since Lyapunov’s seminal work [7], linear stability theory has served as a fundamental reference point. Because it generically provides a qualitative depiction of the dynamical behaviour in the vicinity of fixed points (Hartman–Grobman’s theorem [11]), it is a useful tool to study dynamical properties of nonlinear dynamical systems, and their various attractors. In this paper, we showed that the methodology used to quantify local dynamical stability also provides a measure of local structural stability. In particular, our measures of dynamical and structural stability can be transposed to discrete-time dynamical systems,² which are important in their own right, but also to deal with limit cycles of continuous-time systems, after making a stroboscopic section of trajectories using the Poincaré map [29]. All in all, this suggest that our theory could serve as a benchmark to improve global, quantitative analysis of structural stability.

Finally, it should be noted that we constructed our measures of dynamical stability to mimic empirical approaches to estimate stability from time-series data, in which the fluctuations around a fixed mean can be understood as the effect of stochastic perturbations of an equilibrium [30,17]. Thus, in the setting of near equilibrium dynamics, our work reveals a strong conceptual link between pragmatic empirical views on stability and the more abstract concept of structural stability. Furthermore, as discussed above, in the linear theory, it is not necessary to consider worst-case scenarios (an unpractical notion from an empirical stand point) for a connection between these two stability notions to hold. To further bridge the gap between empirical and theoretical approaches, it could be worthwhile to investigate the most probable scenarios, given a prior distribution on the set of perturbation directions.

Appendix A. Dominant eigenvalues of perturbed lifted operator

Recall that $\hat{A}$ is the lifted operator defined from a stable real matrix A and acting on any matrix X as $\hat{A}(X)=AX+X{A}^{\mathrm{\top }}$, and that $\mathcal{P}$ is defined from an arbitrary sequence of real matrices P_k as $\mathcal{P}(X)=\sum _k{P}_{k}X{P}_k^{\mathrm{\top }}$. Assume that the perturbed operator $\hat{A}+\mathcal{P}$ lies on the boundary between stability and instability, that is,

$$\alpha (\hat{A}+\mathcal{P})=0.$$

Here, we show that any operator of the form

$${\mathcal{A}}_{ϵ}=\hat{A}+ϵ\mathcal{P}\text{with}\hspace{0.17em}0\le ϵ<1,$$

must have a real-dominant eigenvalue λ_ϵ<0, associated with an eigenvector X_ϵ. This would show, in particular, that ${\mathrm{\lambda }}_{ϵ}\to 0$ as ϵ goes to 1, so that

$${\mathcal{A}}_{ϵ}(X_{ϵ})\to (\hat{A}+\mathcal{P})X_1=0,$$

an identity that was previously needed to prove that ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)\ge {\mathcal{S}}_{\mathrm{DYN}}^{\mathrm{w}}(A)$.

To show this, suppose the converse, that is: that the dominant eigenvalues of ${\mathcal{A}}_{ϵ}$ all have non-zero imaginary parts. Arbitrarily, small perturbations of the matrices A and P_k can ensure that the operator ${\mathcal{A}}_{ϵ}$ has a unique dominant eigenvalue λ_ϵ=iω_ϵ+α_ϵ up to complex conjugacy, associated with left and right eigenvectors $X_{\mathrm{L}}^{ϵ},\hspace{0.17em}{X}_{\mathrm{R}}^{ϵ}$, respectively. Choose a covariance matrix Σ such that

$$⟨X_{\mathrm{L}}^{ϵ},\mathrm{\Sigma }⟩=\text{Tr}\hspace{0.17em}\mathrm{\Sigma }{X}_{\mathrm{L}}^{ϵ}\ne 0,$$

Note that if there exist no such Σ we can disregard the eigenvalue λ_ϵ and its associated eigenspace as they will play no role on the dynamics restricted to positive semi-definite matrices. Indeed, by construction, the semi-group

$${\{{\mathrm{e}}^{t{\mathcal{A}}_{ϵ}}\}}_{t>0},$$

preserves the set of real positive matrices, and it is the restriction to that set that is of interest to us. In particular, the starting point C₀=Σ becomes, as time flows forward

$$C_t={\mathrm{e}}^{{\alpha }_{ϵ}t}\{{\mathrm{e}}^{\mathrm{i}{\omega }_{ϵ}t}⟨X_{\mathrm{L}}^{ϵ},\mathrm{\Sigma }⟩X_{\mathrm{R}}^{ϵ}+\text{c.c.}+o(1)\}.$$

Writing $Z_{ϵ}=⟨X_{\mathrm{L}}^{ϵ},\mathrm{\Sigma }⟩X_{\mathrm{R}}^{ϵ}$, we see that C_t converges to

$${\mathrm{e}}^{{\alpha }_{ϵ}t}\{\cos ({\omega }_{ϵ}t)\mathrm{\Re }(Z_{ϵ})-\sin ({\omega }_{ϵ}t)\mathrm{\Im }(Z_{ϵ})\},$$

which rotates at frequency ω_ϵ. It therefore cannot be positive for all t which it should when the subdominant terms in C_t become negligible. We thus get a contradiction, hence λ_ϵ must be real.

To summarize, we have shown that, modulo arbitrary small perturbations of the matrices A and P_k, the dominant eigenvalue of ${\mathcal{A}}_{ϵ}$ is simple and real. Because the spectrum depends continuously on the matrix entries [31], this implies that among the dominant eigenvalues of ${\mathcal{A}}_{ϵ}$ one was already real.

Appendix B. Ordering of structural stability measures

In the theorem, we claim that stochastic structural stability relates to the stability radius of matrices following the general inequality (illustrated in figure 2)

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}\le 2{\mathcal{S}}_{\mathrm{STR}}^c,$$

with equality when the Jacobian matrix at the equilibrium is normal. Here, we prove this fact. Let us start by stating a lemma from linear algebra.

Lemma B.1. —

For any invertible matrix B acting on ${\mathbb{C}}^n$, it holds that

$$\underset{x\in {\mathbb{C}}^n;\parallel x\parallel =1}{min}\parallel Bx\parallel ={(\underset{y\in {\mathbb{C}}^n;\parallel y\parallel =1}{max}\parallel B^{-1}y\parallel )}^{-1}.$$

Proof. —

Take x_*=B⁻¹y/∥B⁻¹y∥ with y normalized and realizing the maximum of ∥B⁻¹y∥. By construction

$$\underset{x\in {\mathbb{C}}^n;\parallel x\parallel =1}{min}\parallel Bx\parallel \le \parallel B{x}_{\ast }\parallel ={(\underset{y\in {\mathbb{C}}^n;\parallel y\parallel =1}{max}\parallel B^{-1}y\parallel )}^{-1}.$$

To show that taking the minimum over all normalized elements x does not give anything smaller, it suffices to choose y_*=Bx/∥Bx∥ with x normalized and realizing the minimum of ∥Bx∥. By construction

$$\underset{y\in {\mathbb{C}}^n;\parallel y\parallel =1}{max}\parallel B^{-1}y\parallel \ge \parallel B^{-1}{y}_{\ast }\parallel ={(\underset{x\in {\mathbb{C}}^n;\parallel x\parallel =1}{min}\parallel Bx\parallel )}^{-1},$$

which is equivalent to

$$\underset{x\in {\mathbb{C}}^n;\parallel x\parallel =1}{min}\parallel Bx\parallel \ge {(\underset{y\in {\mathbb{C}}^n;\parallel y\parallel =1}{max}\parallel B^{-1}y\parallel )}^{-1},$$

proving the lemma. ▪

With this result in hand, we can write, for any stable real matrix A,

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)=\parallel {\hat{A}}^{-1}{\parallel }^{-1}=\underset{\parallel X{\parallel }_{\mathrm{F}}=1}{min}\parallel \hat{A}X{\parallel }_{\mathrm{F}}.$$

In particular, for any normalized matrix X,

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)\le \parallel \hat{A}X{\parallel }_{\text{F}}=\parallel AX+X{A}^{\mathrm{\top }}{\parallel }_{\mathrm{F}}.$$

Choosing X as a rank-one orthonormal projector, X=ww*, gives, for any real ω

$$\begin{array}{rl}{\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)& \le \parallel (A\mathit{\text{w}}){\mathit{\text{w}}}^{\ast }+\mathit{\text{w}}{(A\mathit{\text{w}})}^{\ast }{\parallel }_{\mathrm{F}}\\ & \le \parallel ((\mathrm{i}\omega -A)\mathit{\text{w}}){\mathit{\text{w}}}^{\ast }+\mathit{\text{w}}{((\mathrm{i}\omega -A)\mathit{\text{w}})}^{\ast }{\parallel }_{\mathrm{F}}.\end{array}$$

On the other hand, we also have, using lemma B.1, that

$${\mathcal{S}}_{\mathrm{STR}}^c(A)=\parallel {(\mathrm{i}\omega -A)}^{-1}{\parallel }^{-1}=\underset{\omega ,\parallel \mathit{\text{w}}\parallel =1}{inf}\parallel (\mathrm{i}\omega -A)\mathit{\text{w}}\parallel .$$

In the upper bound of ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)$, choosing ω to be the system’s resonant frequency and w the associated minimizing vector of ∥(iω−A)w∥, and then invoking the triangular inequality, yields

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)\le 2{\mathcal{S}}_{\mathrm{STR}}^c(A).$$

Let us now show that equality holds whenever A is normal. First of all, for normal A, ${\mathcal{S}}_{\mathrm{STR}}^c(A)$ coincides with the spectral abscissa α(A). This is a consequence of the following equality, valid for any normal matrix A and complex number z away from the spectrum of A [8]

$$\parallel {(z-A)}^{-1}\parallel =\frac{1}{\text{dist}(z,\text{spect}(A))}.$$ B 1

where dist(⋅,⋅) stands for the Hausdorff distance between subsets of the complex plane, equipped with the Euclidean metric. Indeed, taking z=iω, where ω is the imaginary part of the dominant eigenvalue of A, gives ${\mathcal{S}}_{\mathrm{STR}}^c(A)=\alpha (A)$. In addition, if A is normal, $\hat{A}$ is also automatically normal. Because A is diagonalizable, we can express the spectrum of $\hat{A}$ from the one of A. Indeed, if {(λ_i,u_i)}_i are the complete eigenpairs of A, then ${\{({\mathrm{\lambda }}_i+{\overline{\mathrm{\lambda }}}_j,\hspace{0.17em}{\mathit{\text{ u}}}_i{\mathit{\text{ u}}}_j^{\ast })\}}_{i,j}$ are the complete eigenpairs of $\hat{A}$. If λ₀ is the dominant eigenvalue of A, then by definition −ℜ(λ₀)=α(A), and thus $\{-2\alpha (A),2{\mathrm{\lambda }}_0,2{\overline{\mathrm{\lambda }}}_0\}$ are dominant eigenvalues of $\hat{A}$. Applying the above identity (B 1) to the normal operator $\hat{A}$, namely

$$\parallel {(z-\hat{A})}^{-1}\parallel =\frac{1}{\text{dist}(z,\text{spect}(\hat{A}))},$$

and taking z=0 gives $\parallel {\hat{A}}^{-1}\parallel =1/2\alpha (A)$, hence ${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{w}}(A)=2\alpha (A)=2{\mathcal{S}}_{\mathrm{STR}}^c(A)$, which is the expected equality.

Finally, because the real constant perturbation, $P=\alpha (A)\mathbb{I}$ is always sufficient to destabilize any stable matrix A, in the light of the previous result, we see that for normal matrices

$${\mathcal{S}}_{\mathrm{STR}}^{\mathrm{\Re }(c)}(A)={\mathcal{S}}_{\mathrm{STR}}^c(A)$$

completing the proof of the theorem.

Data accessibility

This paper has no data.

Authors' contributions

Both authors contributed equally to this study.

Competing interests

The authors declare no conflict of interest.

Funding

This work was supported by the TULIP Laboratory of Excellence (ANR-10-LABX-41), the AnaEE France project (ANR-11-INBS-0001) and by the BIOSTASES advanced grant, supported by the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 666971).