Table 2.
|
Algorithm 2 Decycle: REMOVE ALL CYCLES FROM A GRAPH | |
Require: A directed graph  , including: , including: | |
a function 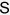 (e) that specifies the successors to node e, and (e) that specifies the successors to node e, and | |
a function 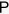 (e) that specifies the predecessors to node e (e) that specifies the predecessors to node e
| |
| a function f(e) that specifies frequency of epitope e in the population | |
| Require: Functions STRONGLY_CONNECTED_COMPONENTS and SHORTEST_PATH, both are provided by NetworkX software package41 | |
| 1: repeat | |
2: J ← STRONGLY_CONNECTED_COMPONENTS ( ) ) | |
▹ J is a list of all components; each component is a list of nodes in

|
|
| 3: J ← J − {j ∈ J, such that |j| = 1} | |
| ▹ Discard all single-node components – no cycles there! | |
| 4: for all j ∈ J do | ▹ For each component |
| 5: repeat | |
| 6: Choose (a, b) ∈ j | ▹ Randomly choose two nodes from the selected component |
7: C ← CYCLEFROMTWONODES( , a, b) , a, b) |
|
| 8: if C ≠ ∅ then | |
9: (ea, eb) ← WEAKEDGEINCYCLE( , C) , C) |
|
10: Remove edge (ea, eb) from 
|
|
| 11: until C = ∅ | |
| 12: until J = ∅ | ▹  is acyclic; we are done.
is acyclic; we are done. |
13: procedure CYCLEFROMTWONODES( , a, b) , a, b) |
|
14: Pab ← SHORTEST_PATH( , a, b) , a, b) |
|
15: Pba ← SHORTEST_PATH( , a, b) , a, b) |
|
| 16: if either call to SHORTEST_PATH fails then | |
| 17: C ← ∅ | |
| 18: else | |
| 19: C ← Pab + Pba | ▹ Merge two paths into a cycle |
| 20: return C | |
21: procedure WEAKEDGEINCYCLE( , C) , C) |
|
| 22: Write C as a list of nodes [e1, …, ek] and edges [(e1, e2), (e2, e3), …, (ek, e1)] | |
| 23: for all (ei, ej) in [(e1, e2), (e2, e3), …, (ek, e1)] do | |
| 24: vij ← f(ei) + f(ej) | ▹ v is heuristic “value” of edge |
25: vij ← vij + f (ei) if |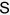 (ei)| = 1 (ei)| = 1 |
▹ Add value if cutting edge would isolate ei |
26: vij ← vij + f (ej) if |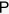 (ej)| = 1 (ej)| = 1 |
▹ Add value if cutting edge would isolate ej |
| 27: Let io, jo ← argmin vij | |
28: return(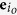 , ,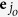 ) ) |
▹ return lowest-value edge in cycle |
|
Algorithm 3 Cocktail: FIND (AND ITERATIVELY REFINE) A SET OF m ANTIGENS | |
Require: Directed Acyclic Graph  , including , including | |
| a function f (e) that specifies frequency of epitope e in the population | |
Require: Function EPIGRAPH( , f) that returns a sequence q, corresponding to a path through the graph , f) that returns a sequence q, corresponding to a path through the graph  that maximizes that maximizes 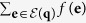
| |
| ▷See Algorithm 1 | |
1:  ← ∅ ← ∅ |
|
2: f*(e) ← f (e) for all epitopes e ∈ 
|
▷Initialize |
| 3: for n = 1 … m do | ▷Sequential solution |
4: qn ← EPIGRAPH( , f*) , f*) |
▷Compute next antigen sequence qn |
5:  ← ←  ∪ {qn} ∪ {qn} |
▷Add qn to vaccine |
6: for e ∈ 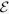 (qn) do (qn) do
|
▷Now that e is in the vaccine |
| 7: f*(e) ← 0 | ▷No credit for including e in subsequent antigens |
▷At this point, f*(e) = 0 for all
e ∈ 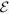 ( ( ) ) |
|
| 8: repeat | ▷Iterative Refinement (optional) |
| 9: for n = 1 … m do | |
10:  ← ← − {qn} − {qn} |
▷Remove sequence qn from vaccine |
11: for e ∈ 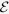 ( ( ) − ) − 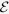 (qn) do (qn) do
|
▷With e not in the vaccine anymore, |
| 12: f*(e) ← f(e) | ▷f*(e) gives credit for including e in subsequent antigens |
13: qn ← EPIGRAPH( , f*) , f*) |
▷Compute replacement for old sequence qn |
14:  ← ←  ∪ {qn} ∪ {qn} |
▷Add qn to vaccine |
15: f*(e) ← 0 for all e ∈ 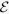 (qn) (qn) |
|
| 16: until no change in q1, …, qm | |
17: return cocktail of m sequences:  = {q1, …, qm} = {q1, …, qm} |
|
| Algorithm 4 TTV: TAILORED THERAPEUTIC VACCINE | |
Require: Sequence set 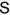 = {s1, …, sN}, = {s1, …, sN}, | |
Require: Directed Acyclic Graph, 
| |
Require: Function EPIGRAPH( , f) that returns a sequence q, corresponding to a path through the graph , f) that returns a sequence q, corresponding to a path through the graph  that maximizes that maximizes 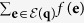 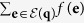
| |
| ▷See Algorithm 1 | |
| 1: Define u(s, e) = 1 if epitope e appears in sequence s | ▷i.e., if
e ∈ 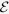 (s) (s) |
2: f(e) ← (1/N) 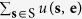
|
▷Frequency of epitope
e
in sequence set
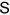
|
3: qo ← EPIGRAPH( , f) , f) |
▷qo
is centroid of the full data set
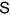
|
4: Randomly select m − 1 sequences from 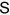 ; call them q1, …, qm−1. ; call them q1, …, qm−1. |
|
| 5: repeat | |
6: Initialize: 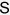 1 = … = 1 = … = 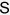 m−1 = ∅ m−1 = ∅ |
|
| 7: for i = 1…N do | ▷Loop over sequences |
| 8: for n = 1…m−1 do | ▷Loop over centroids |
9: 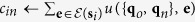
|
▷Coverage of sequence si by antigens {qo, qn} |
| ▷Here, u({qo, qn}, e) = max[u(qo,. e), u(qn, e)] | |
| 10: n ← argmaxn′cin′ | |
11: 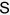 n ← n ← 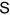 n ∪ {si} n ∪ {si} |
▷Put
si
into cluster
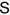 n n
|
| 12: for n = 1…m − 1 do | ▷Loop over clusters |
13: f (n)(e)(1/N) ← 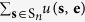
|
▷Frequency of
e
in sequence cluster
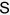 n n
|
14: f (n)(e) ← 0 for all e ∈ 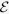 (qo) (qo) |
▷No credit for epitopes already covered by qo |
15: qn ← EPIGRAPH( , f (n)) , f (n)) |
▷New centroid for
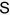 n n
|
| 16: until convergence | |
| 17: return tailored therapeutic vaccine: qo, q1, …, qm−1 | |
