Identification of MicroRNA Precursors with Support Vector Machine and String Kernel

Abstract

MicroRNAs (miRNAs) are one family of short (21–23 nt) regulatory non-coding RNAs processed from long (70–110 nt) miRNA precursors (pre-miRNAs). Identifying true and false precursors plays an important role in computational identification of miRNAs. Some numerical features have been extracted from precursor sequences and their secondary structures to suit some classification methods; however, they may lose some usefully discriminative information hidden in sequences and structures. In this study, pre-miRNA sequences and their secondary structures are directly used to construct an exponential kernel based on weighted Levenshtein distance between two sequences. This string kernel is then combined with support vector machine (SVM) for detecting true and false pre-miRNAs. Based on 331 training samples of true and false human pre-miRNAs, 2 key parameters in SVM are selected by 5-fold cross validation and grid search, and 5 realizations with different 5-fold partitions are executed. Among 16 independent test sets from 3 human, 8 animal, 2 plant, 1 virus, and 2 artificially false human pre-miRNAs, our method statistically outperforms the previous SVM-based technique on 11 sets, including 3 human, 7 animal, and 1 false human pre-miRNAs. In particular, pre-miRNAs with multiple loops that were usually excluded in the previous work are correctly identified in this study with an accuracy of 92.66%.

Introduction

MicroRNAs (miRNAs) are short (~22 nt) endogenous non-coding RNA molecules that regulate protein-coding gene expression in animals, plants and viruses through the RNA interference pathway. There are three main steps to form a mature miRNA: (1) an miRNA gene is transcribed into a primary miRNA (pri-miRNA) by Pol II enzyme; (2) this pri-miRNA is cleaved to a 70–110 nt miRNA precursor (pre-miRNA) with a stem-loop hairpin structure by Drosha RNase III endonuclease in animals or by Dicer-like enzyme in plants; (3) such a pre-miRNA is cleaved into miRNA:miRNA^* duplex and a mature miRNA is released to regulate targeted gene expression ^{1., 2., 3., 4.}. Since experimental cloning methods for searching new miRNAs are low efficient, time consuming and very expensive, computational approaches are more and more popular to choose miRNA candidates for further experimental validation ^{5., 6., 7., 8.}.

It has been observed that pre-miRNAs and their secondary structures encode more discriminative and characteristic information than their corresponding mature miRNAs do ^{5., 6., 7., 8.}. Thus, most computational methods utilize pre-miRNA sequences and/or their secondary structures to detect miRNAs or pre-miRNAs. It is noted that secondary structures are also depicted as sequences by using brackets and dots in RNAfold (9). In this study, we regard the computational identification of miRNAs or pre-miRNAs as a pattern classification problem and group the existing methods into two categories: gradually hierarchical approaches and directly discriminative ones.

The gradually hierarchical computational techniques mainly include miRscan ^{10., 11.}, miRSeeker (12) and miRAlign (13) for animals, and miRCheck (14) and miRFinder (15) for plants. Their basic strategy is to combine comparative genomics information with pre-miRNA sequences and/or their secondary structures to filter the putative pre-miRNA candidates step by step. For each step, a proper criterion based on a single feature (minimal folding free energy) or a simply linear combination of several features (GC content, length of hairpin loop, etc.), is designed to eliminate most of the hairpins that are not conserved in related species. At last, the remainder becomes miRNA candidates to be further validated by some cloning experiments. However, some true pre-miRNAs may be excluded in the early steps ^{6., 13.}. Furthermore, these methods rely on comparative genomics and are unable to identify new miRNA genes without homologues ^{16., 17.}.

In the discriminative identification methods, a classifier is trained by using positive and negative samples of pre-miRNAs. The former is constructed from true pre-miRNAs and/or their secondary structures, and the latter is from sequence segments with similar stem-loop structures but have not been recognized as true pre-miRNAs ^{16., 18.} or other known RNAs (mRNAs, tRNAs or rRNAs) (17). Machine learning techniques, such as support vector machine (SVM) ^{19., 20.} and random forest (21), have been used to detect true and false pre-miRNAs. In order to fit SVM, Xue et al. (16) extracted 32 triplet features from sequences and secondary structures of true and false pre-miRNAs, while Sewer et al. (17) obtained 40 features from pre-miRNA secondary structures. In Jiang et al. (18), two additional features, P-value and minimal free energy, were combined with the 32 triplet features from Xue et al. (16). However, it is difficult for them to deal with those secondary structures with multiple loops that were excluded in their studies ^{16., 18.}.

In bioinformatics, there are a large number of datasets consisting of symbols (for instance, DNA, RNA and protein sequences) rather than numerical features, thus more attention has been paid to constructing a kernel from two strings or sequences for SVM ^{22., 23., 24.}. It was illustrated that some useful information was missed during converting a DNA sequence into a numerical feature vector for identifying splice junction types (22). Accordingly, several kernels based on weighted Levenshtein distance (WLD) between two DNA sequences were designed and the corresponding classification accuracy was obviously improved on benchmark datasets ^{22., 23., 24.}. To some extent, directly handling sequence data in SVM is better than converting sequences into numerical features in some real applications ^{22., 23., 24.}.

In this study, we utilize pre-miRNA sequences and their secondary structures simultaneously to build a multiplicative string kernel consisting of two exponential kernels, in which the distance measure between two vectors is replaced by the WLD between two sequences (pre-miRNA sequences or secondary structure sequences). Such a kernel is referred to as an exponential string kernel based on WLD. Then we combine this string kernel with SVM to detect true and false pre-miRNAs. We use the same datasets as those in Xue et al. (16) in order to compare our method with it. Trained by 331 true and false human pre-miRNAs, the optimal algorithmic parameters are determined by 5-fold cross validation and grid search scheme, and 5 realizations with different 5-fold partitions are executed. Among 16 independent test sets from 3 human, 8 animal, 2 plant, 1 virus, and 2 artificially false human pre-miRNAs, our method statistically outperforms Xue’s method (16) on 11 sets, including 3 human, 7 animal, and 1 false human pre-miRNAs. Particularly, our method can identify those pre-miRNAs with multiple loops that were excluded in the previous studies ^{16., 18.} with a satisfactory accuracy of 92.66%.

Results and Discussion

Our training set for designing the SVM classifier consists of 331 samples as those in Xue et al. (16), in which 163 positive samples come from true human pre-miRNAs and 168 negative ones from artificially false human pre-miRNAs. There exist three key parameters, including a regularization constant C and two width parameters of exponential kernels γ^sequence and γ^structure, which affect our classification accuracy. To save computational time, the two kernel widths are forced to be identical, that is, γ = γ^sequence= γ^structure. Using 331 training samples, we combine 5-fold cross validation with grid search stategy to find out the optimal values of these parameters. Here C and γ are taken as 2⁰, 2¹, …, 2¹⁰, respectively. Therefore 11×11=121 parameter pairs are executed. The parameter pair corresponding to the highest accuracy based on left-out training samples is considered as an optimal one. When there exist several optimal pairs, all of them are utilized to design the SVM classifier using all training samples, and the accuracies on independent test sets are averaged on all classifiers. In order to enhance statistical significance, 5 realizations with different 5-fold partitions are fulfilled and overall accurcies are averaged on them again.

Table 1, Table 2 list our experimental results on 16 independent test sets, where the best results are indicated by the bold type. Since the SVM classifier is trained by human pre-miRNAs, it is firstly used to detect true and false pre-miRNAs of five test sets from true human (homo sapiens) and artificially false human pre-miRNAs. In Table 1, for the first four sets, our method outperforms Xue’s method (16) on three sets; whereas for one set (Conserved-hairpin), it is 6.23% lower than Xue’s. This would inspire us to improve our approach and analyze this dataset further. Remarkably, those pre-miRNAs with multiple loop secondary structures that were not considered in Xue et al. (16) are identified with a satisfactory overall accuracy of 92.66%. This means that our method can directly deal with pre-miRNAs with multiple loop hairpin structures.

Table 1.

Identification accuracies (%) on human datasets

Test set	Type	Realization							Overall	Xue’s (16)
		1		2	3	4		5
TE-C (Pseudo)	False	92.97	93.11		93.10		93.21	93.15	93.11	88.1
Conserved-hairpin	False	84.66	82.84		81.71		81.62	83.00	82.77	89.0
Homo sapiens (TE-C-real)	True	100.0	96.97		93.33		93.33	96.67	96.06	93.3
Homo sapiens (Updated)	True	94.87	94.87		94.87		94.87	94.87	94.87	92.3
Homo sapiens (Multiple loops)	True	91.84	92.86		92.86		92.86	92.86	92.66	–

Table 2.

Identification accuracies (%) on datasets from 11 species

	Test set	Realization						Overall	Xue’s (16)
		1	2	3	4	5
Animal	Caenorhabditis briggsae	98.43	98.63	100.0	100.0		99.32	99.28	95.9
	Caenorhabditis elegans	86.88	90.00	91.82	91.82		90.00	89.98	86.4
	Drosophila melanogaster	95.77	98.46	97.18	94.68		97.89	96.80	91.5
	Drosophila pseudoobsura	96.98	95.62	92.96	92.02		94.37	94.39	90.1
	Dnio rerio	83.33	83.33	83.33	83.33		83.33	83.33	66.7
	Gallus gallus	78.02	91.61	92.31	92.31		88.47	88.54	84.6
	Rattus norvegicus	75.43	83.64	80.00	80.00		82.00	80.21	80.0
	Mus musculus	93.65	91.67	88.89	88.89		90.28	90.68	94.4
Plant	Arabidopsis thaliana	76.57	85.82	92.00	94.52		84.67	86.72	92.0
	Oryza sativa	78.15	89.97	91.67	92.71		87.50	88.00	94.8
Virus	Epstein Barr Virus	60.00	41.82	40.00	40.00		50.00	46.36	100.0
Overall		87.35	91.64	92.43	92.51		90.80	90.95	90.9

In Table 2, an amount of 581 pre-miRNAs from 11 species ranging from animals, plants and virus are tested in order to demonstrate the identification ability of this method across species, and the results are compared with those in Xue et al. (16). It shows that our method outperforms Xue’s method (16) on eight animal species except mouse (Mus musculus). For two plant species, satisfactory accuracies (86.72% and 88.00%) are achieved, but they are lower than those in Xue et al. (16). This phenomenon possibly results from the more variable lengths of plant pre-miRNAs. Our method fails to detect virus pre-miRNAs with only 46.36% overall accuracy. One reason is that the average length of five virus pre-miRNAs (65.60 nt) is shorter than that of positive training samples (86.49 nt) and is more close to that of negative training samples (82.81 nt). Another reason is that the human being and the virus belong to two distinct kindoms, thus the SVM classifier trained by human being pre-miRNAs is possibly not suitable for detecting virus pre-miRNAs.

The above results show that our method is a better pre-miRNA predictor for animal species. In addition, using 5 realizations with different 5-fold partitions, our results have more reliable statistical significance than those in Xue et al. (16). However, when it is applied to predict virus pre-miRNAs, we have to be cautious.

Conclusion

The computational identification of true and false pre-miRNAs plays an important part in searching new miRNAs. In this study, we construct an exponential string kernel based on WLD between two sequences, in which pre-miRNA sequences and their secondary structures are considered simultaneously as sequences. Combined with this string kernel, SVM is used to detect true and false pre-miRNAs. The optimal algorithemic parameters are selected by 5-fold cross validation and grid search approach. According to our experimental results with five realizations mentioned above, we draw the following conclusions:

• (1)Our SVM classifier trained only by human pre-miRNA samples is very effective to identify human and animal pre-miRNAs. Among 16 independent test sets from 3 human, 8 animal, 2 plant, 1 virus, and 2 artificially false human pre-miRNAs, our method statistically outperforms Xue’s method (16) on 11 sets, including 3 human, 7 animal, and 1 false human pre-miRNAs. However, the identification accuracies on two species of plant pre-miRNAs are a little lower. We also note that our classifier is not suitable for detecting virus pre-miRNAs. It is possible that there exist some distinct characteristics between virus and human pre-miRNAs.
• (2)Our exponential string kernel can capture more discriminative and characteristic information hidden in pre-miRNA sequences and their secondary structures than numerical features did. For animal pre-miRNAs, our string kernel improves the identification accuracies obviously, compared with the general RBF kernel with numerical features used in Xue et al. (16).
• (3)The identification performance depends on the optimal choice of key parameters. It is demonstrated that combining 5-fold cross validation with grid search scheme is an effective method for parameter selection in this study. Five realizations with different partitions make our experimental results more statistically significant.
• (4)Those secondary structures with multiple loops excluded in previous studies ^{16., 18.} can be identified correctly with up to 92.66% overall accuracy in this study. This illustrates that our method can deal with multiple loop secondary structures directly.

In short, it could be concluded that combining SVM and exponential string kernel based on WLD can effectively identify true and false pre-miRNAs by using both pre-miRNA sequences and their secondary structures simultaneously. Our further work will deal with more new test sets, elaborately select all algorithmetic parameters in SVM and WLD, and use this method to search new miRNA candidates.

Materials and Methods

Datasets of pre-miRNAs and their secondary structures

In order to compare our method with Xue’s method, we use the same datasets as they did (16) (Table 3), which can be downloaded from http://bioinfo.au.tsinghua.edu.cn/mirnasvm. Their true miRNAs and pre-miRNAs of 12 species were mainly from the miRNA registry database (release 5.0, Sep. 2004) ^{25., 26.}. There contained 207 human miRNAs at that time, in which 163 and 30 miRNAs without multiple loop hairpin structures were used in Xue et al. (16) as positive training and test samples, respectively, as shown in Table 3 as positive samples (hsa) and TE-C-real. In this study, we pick up the 14 miRNAs with multiple loops that were excluded in Xue et al. (16) as one of our test sets. The other 11 species were involved in the same database release 5.0, although 39 updated human miRNAs have been reported after this release.

Table 3.

Summary of 18 true and false pre-miRNA datasets

	Dataset	Type	Size	Length (nt)
				Minimal	Maximal	Average
Human	Positive training samples (hsa)	True	163	62	119	86.49
	Negative training samples (pseudo)	False	168	63	110	82.81
	TE-C (pseudo)	False	1,000	62	119	84.27
	Conserved-hairpin	False	2,444	100	100	100
	TE-C-real	True	30	62	110	84.80
	Updated	True	39	58	95	78.49
	Multiple loops	True	14	80	110	96.29
Animal	Caenorhabditis briggsae	True	73	72	116	97.96
	Caenorhabditis elegans	True	110	72	110	98.05
	Drosophila melanogaster	True	71	63	110	86.35
	Drosophila pseudoobsura	True	71	62	110	86.70
	Dnio rerio	True	6	73	99	89.17
	Gallus gallus	True	13	64	107	90.00
	Rattus norvegicus	True	25	68	105	90.64
	Mus musulusi	True	36	61	108	83.06
Plant	Arabidopsis thaliana	True	75	80	263	127.81
	Oryza sativa	True	96	82	207	123.28
Virus	Epstein Barr Virus	True	5	62	70	65.60
Overall			4,439

The artificially false pre-miRNAs consisted of sequence segments (protein coding regions of human RefSeq genes and gene regions on human chromosome 19) that had similar stem-loop hairpin structures as true pre-miRNAs but had not been recognized as true pre-miRNAs. In Xue et al. (16), 8,494 false pre-miRNAs were constructed from the protein coding sequences of human RefSeq genes, in which 168 and 1,000 of them were selected as negative training samples and test samples [TE-C (pseudo)]. Meanwhile, from gene regions on human chromosome 19, 2,444 false pre-miRNAs with the same length of 100 nt were built as a test set (Conserved-hairpin) in Xue et al. (16).

It is noted that only 331 training samples including 163 positive and 168 negative samples are used to design the SVM classifier in this study, just as in Xue et al. (16), while the other 16 independent datasets are left out to validate the identification accuracies of our method.

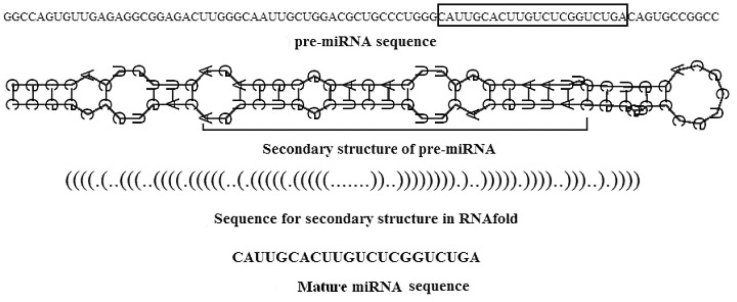
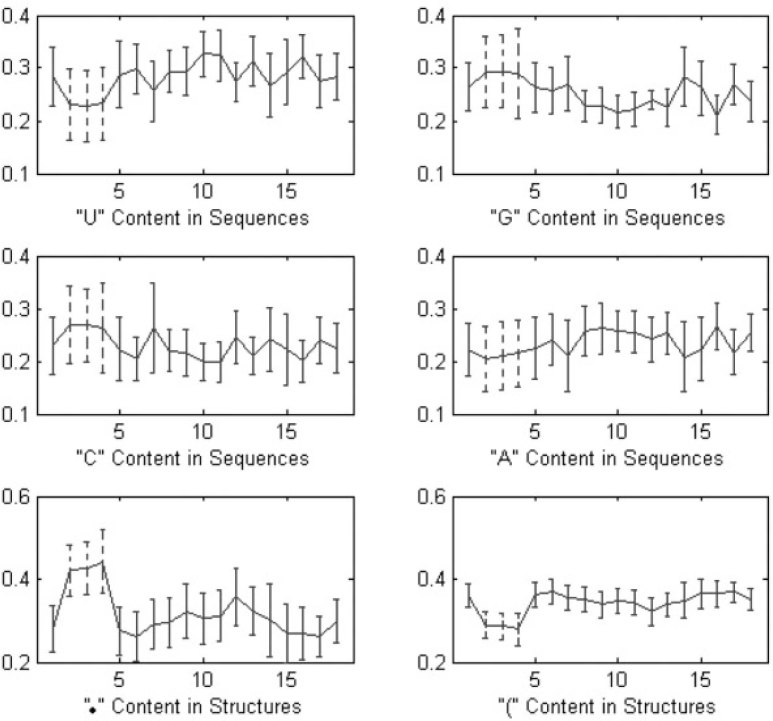
The pre-miRNA sequences consist of four nucleotides (A, U, G, C). Their secondary structures predicted by RNAfold (9) are depicted as sequences with brackets and dots indicating two kinds of status of each nucleotide: “paired” and “unpaired”. The left bracket “(” implies that the paired nucleotide is located near the 5′-end and can be paired with the other nucleotide at the 3′-end, which is denoted by a right bracket “)”. In Figure 1, the pre-miRNA sequence, its secondary structure and sequence depiction, and the mature miRNA sequence of human miRNA has-mir-25 are illustrated. Figure 2 shows the “U, G, C, A” contents in pre-miRNA sequences and the “.” and “(” contents in secondary structures of 18 datasets. It can be observed that the upper four plots could not illustrate the obvious difference between false pre-miRNAs (from the second set to the fourth one denoted by dash lines) and true pre-miRNA (the first set and the others). In the lower two plots, the relative distinction between true and false pre-miRNAs is visual. However, such discriminative information is not enough to detect true and false pre-miRNAs satisfactorily. The existing methods attempt to extract more useful information from pre-miRNA sequences and/or their secondary structures to further improve the identification performance ^{16., 17., 18.}.

Fig. 1.

Illustration of the pre-miRNA sequence, its secondary structure and sequence depiction, and the mature miRNA sequence of human miRNA has-mir-25.

Fig. 2.

Plots of the U, G, C, A contents in pre-miRNA sequences and the “.” and “(” contents in secondary structures of 18 datasets, where the horizontal axis denotes 18 datasets listed in Table 3 and the vertical axis indicates the mean and standard deviation of content for each dataset. The second to fourth datasets (dash lines) are three false pre-miRNA sets, while the others represent 15 true pre-mRNA sets.

In this study, both pre-miRNA sequences with four nucleotides and their secondary structure sequences with brackets and dots are directly considered as symbol sequences and are used to construct an exponential string kernel based on WLD for SVM.

SVM

SVM is a nonlinearly supervised classification method for binary problem ^{19., 20.}. For a given training set {x_i, y_i}, x_i ∈ R^d, y_i ∈ {+1,−1}, i = 1,…,l, where +1 or −1 corresponds to positive or negative training samples, respectively, SVM is given to solve a quadratic programming as follows:

$$\begin{array}{l}\underset{{\alpha }_i}{\min }\frac{1}{2}\sum _{i,j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(x_i,x_j)-\sum _{i=1}^l{\alpha }_i\\ \mathrm{s.t.}\sum _{i=1}^l{\alpha }_i{y}_i=0\\ 0\le {\alpha }_i\le C,i=1,\dots ,l\end{array}$$ (1)

where α_i (i = 1,…, l) is the coefficients to be solved, C is the regularization constant that can control the trade-off between the number of errors and the complexity of classifier, and k(x_i, x_j) is the kernel function between two vectors. Those training samples with α_i > 0 (i = 1,…,l) are referred to as support vectors.

For a new input vector x, the SVM classifier assigns it to one of two classes according to the following nonlinearly discriminant function:

$$f(x)=sign\left(\sum _{i=1,{\alpha }_i>0}^l{\alpha }_i{y}_{i}k(x_i,x)+\beta \right)$$ (2)

where the threshold β is calculated for some support vectors (0 < α_i < C) using KKT condition:

$$\left(\sum _{j=1,{\alpha }_j>0}^l{\alpha }_j{y}_{j}k(x_i,x_j)+\beta \right)y_i=1$$ (3)

In order to fit WLD conveniently, we choose an exponential kernel (22) as:

$$k(x,y)=\exp \left(\frac{-||x-y||}{\gamma }\right)$$ (4)

where generally ||x – y|| denotes the Euclidean distance between two numerical vetors and γ denotes the kernel width. In the next step, this distance is replaced by WLD between two sequences or strings with different lengths.

Exponential string kernel based on WLD

For two given strings or sequences a and b, there are three string-to-string correction operations: (1) deletion, where some symbols in string a are removed; (2) insertion, where some symbols are added into string b; and (3) substitution, where some symbols in string a are replaced by someone in string b. Through the three operations, the string a can be transformed into the string b step by step.

In bioinformatics, the widely used similarity measure between two sequences is edit distance (or Levenshtein distance) (27), which is defined as the smallest number of correction operations converting a into b. When three operations indicate different biological meanings, it is necessary to choose different weights for different operations. WLD is defined as the minimal total weights of single symbol deletions, insertions and substitutions to convert a into b ^{28., 29.}. It is noted that when the insertion weight is identical to the deletion one, WLD still satisfies the distance definition in functional analysis.

Let a_i and b_j be two substrings from the first i and j symbols of a and b, respectively. The WLD between them (d_i,j) can be calculated according to the following dynamic programming algorithm ^{29., 30.}:

$$\begin{array}{l}{d}_{0,0}=0\\ d_{i,0}=d_{i-1,0}+w^D\\ d_{0,j}=d_{0,j-1}+w^I\\ d_{i,j}=\min (d_{i-1,j}+w^I,d_{i-1,j-1}+w^s,d_{i,j-1}+w^D)\\ i=1,\dots ,\left|a\right|,j=1,\dots ,\left|b\right|\end{array}$$ (5)

where w^I, w^D and w^S denote different weights for insertion, deletion and substitution operations, and |a| and |b| are the lengths of two strings. In this case, the WLD between strings a and b is d_|a|,|b|, which is used to replace the Euclidean distance between two vectors in Equation 4 in this study.

In our experiments, we utilize w^I = w^D=1 for insertion and deletion operations. For substitution operation, w^S=0 if two symbols in a and b are identical, otherwise w^S=3. This implies that the substitution operation between two different symbols is inhibited. Thus, the WLD d_|a|,|b| varies from 0 to |a| + |b|, which denotes the length summation of two strings. In order to eliminate the impact of string length, the original WLD is divided by |a| + |b|. In this case, the new WLD’s value ranges between 0 and 1, but we still call this normalized WLD as WLD.

In RNAfold (9), the secondary structure of pre-miRNA is still depicted as a sequence as shown in Figure 1. In our study, pre-miRNA sequences and their secondary structures are taken into account simultaneously, therefore the corresponding exponential string kernel is defined as the multiplication of two exponenntial kernels based on WLD:

$$k(p_i,p_j)=\exp \left(-\frac{d^{\mathit{sequence}}(p_i,p_j)}{{\gamma }^{\mathit{sequence}}}\right)\exp \left(-\frac{d^{\mathit{structure}}(p_i,p_j)}{{\gamma }^{\mathit{structure}}}\right)$$ (6)

where d^sequence and d^structure represent WLD between two sequences and between two secondary structures for pre-miRNA p_i and p_j, and γ^sequence and γ^structure denote their kernel widths, respectively.

A quadratic programming solver “pr-loqo” in C language (http://www.kernel-machines.org/software) was used to train the SVM classifier and a function for WLD was developed by us in C language. The whole software was executed on a computer of P4 3.0 G with 1,024 M RAM using VC6.0 compiler.

Authors’ contributions

JHX collected main datasets, designed and implemented the software, conducted experiments and wrote this manuscript. FL checked and modified this manuscript according to biological viewpoint. QFS prepared and preprocessed some datasets. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.