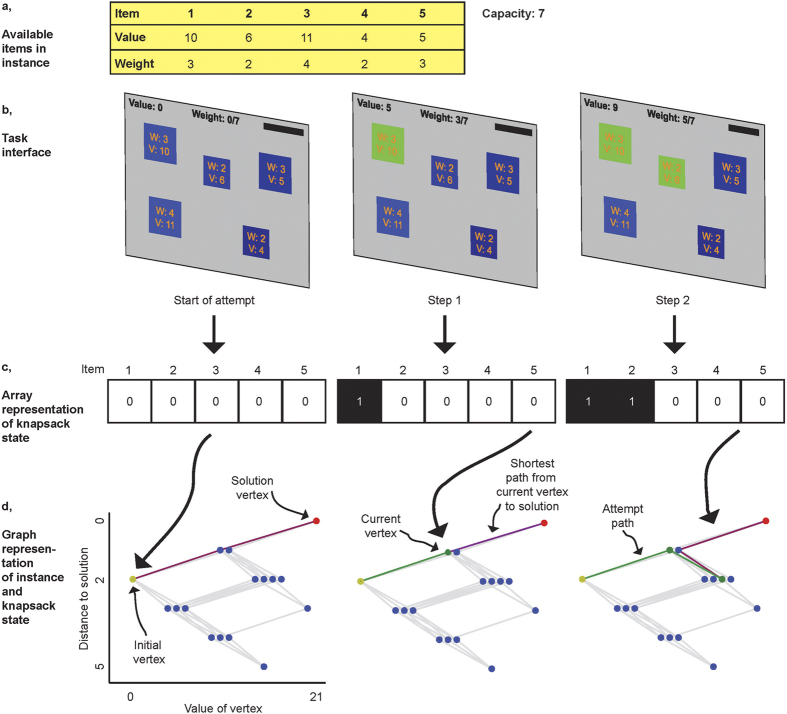
Figure 1. Overview of experimental paradigm.

(a) Example instance of the 0–1 knapsack problem with five items. The goal is to find the subset of available items that maximises total value of the knapsack, subject to a capacity constraint. Values and weights of available items are provided in the table. The capacity of the knapsack is 7. (b) In the experiment, instances were presented on a computer screen. Each item was represented by a square. An item could be added to and removed from the knapsack by clicking on it. Selected items were displayed in green. (c) The state of the knapsack can be represented by an array of 0 s and 1 s with length equal to the number of items available. (d) Admissible states (possible compositions of the knapsack that do not violate the weight constraint) can be represented as vertices in a graph. The position of a vertex on the abscissa is determined by the value of the knapsack it represents, and the position on the ordinate is determined by the distance, in item space, of the vertex from the optimal solution, i.e., by the number of items that need to be removed and added in order to reach the optimal solution (CG; see Supplementary Methods 1.2).