Ab initio structure determination from prion nanocrystals at atomic resolution by MicroED

Significance

Microelectron diffraction (MicroED) is a cryo-EM method capable of determining atomic resolution macromolecular structures from nanocrystals of dose-sensitive biological macromolecules. To date, MicroED requires a reasonably accurate guess of the positions of atoms in a structure to solve it, a technique known as molecular replacement. We now show that this need for prior knowledge about a structure is eliminated in cases when crystals diffract to atomic resolution, relying only on the accuracy of the MicroED intensity measurements. Our findings provide a basis for solving structures from tiny crystals that diffract to high resolution, but are presently disregarded because of their small size.

Abstract

Electrons, because of their strong interaction with matter, produce high-resolution diffraction patterns from tiny 3D crystals only a few hundred nanometers thick in a frozen-hydrated state. This discovery offers the prospect of facile structure determination of complex biological macromolecules, which cannot be coaxed to form crystals large enough for conventional crystallography or cannot easily be produced in sufficient quantities. Two potential obstacles stand in the way. The first is a phenomenon known as dynamical scattering, in which multiple scattering events scramble the recorded electron diffraction intensities so that they are no longer informative of the crystallized molecule. The second obstacle is the lack of a proven means of de novo phase determination, as is required if the molecule crystallized is insufficiently similar to one that has been previously determined. We show with four structures of the amyloid core of the Sup35 prion protein that, if the diffraction resolution is high enough, sufficiently accurate phases can be obtained by direct methods with the cryo-EM method microelectron diffraction (MicroED), just as in X-ray diffraction. The success of these four experiments dispels the concern that dynamical scattering is an obstacle to ab initio phasing by MicroED and suggests that structures of novel macromolecules can also be determined by direct methods.

Macromolecular crystallography must overcome the lack of a measurable phase for each diffraction intensity (1). In X-ray crystallography, when a sufficiently similar structure has been determined, phases from the known structure can be applied to the measured structure factors and refined to provide a new solution (2). Alternatively, the phase problem can be experimentally overcome by use of isomorphous differences, anomalous scattering, or direct methods (3, 4). Methods for ab initio structure determination from measured intensities have been applied to X-ray crystallography data since the mid-1930s (5). The direct method is an ab initio approach to phasing that relies on the relationships between measured structure factors, which inform about their phases, as well as constraints on the positions of atoms in real space (1, 6, 7). The direct-methods approach becomes feasible when a crystal diffracts strongly enough that the intensities can be measured at a resolution better than 1.2 Å (8). This limit follows from the need to resolve atoms as separate features (as required by this method). Data must be recorded from reflecting planes spaced more closely than the interatomic distances. The first structures to be solved by this approach were small atomic assemblies containing few atoms. Since then, a number of small-molecule and macromolecular structures have been determined by direct methods (6, 7, 9–11), including the structure of cytochrome C₃, with 2,208 atoms (12).

Cryo-EM methods that are based on imaging, such as single-particle and tomographic techniques, benefit from the direct measurement of phases (13, 14). For these techniques, phases are encoded in the images, which are the convolution of the projected Coulomb potential of the sample with the contrast transfer function of the microscope. Such an advantage can also exist when crystals are imaged (15, 16). In contrast, phases are lost when only diffraction data are collected, either from 2D crystals by electron crystallography or from 3D crystals by microelectron diffraction (MicroED), just as in X-ray crystallography (15, 17). That is because electron-diffraction micrographs are measurements of the back focal plane of the electromagnetic objective lens in an electron microscope (18). They represent the squared magnitudes of a Fourier transform of the crystal being imaged.

When high-resolution intensities collected using MicroED are combined with phases calculated from preexisting models by the method of molecular replacement, they result in atomic resolution structures (19–22). However, to date, no other X-ray crystallographic method for experimental phase determination has been adapted to MicroED. Because MicroED is capable of producing atomic resolution data, direct methods approaches used in X-ray crystallography should be applicable to MicroED. The influence of dynamical scattering on the measured intensities was thought to limit accurate determination of structure factors (23–26). The hypothesis of whether these effects limit ab initio determination of macromolecular structures from protein nanocrystals has been difficult to test because a crystal formed from macromolecules has yet to diffract to better than 1.2 Å by electron-based techniques. Using ultra-low-dose cryo-EM data collection, we now demonstrate experimental phasing of peptide nanocrystals for MicroED at 1.0-Å resolution—an important step in the determination of novel macromolecular structures and a milestone for atomic resolution cryo-EM of dose-sensitive samples.

Results

We investigated nanocrystals of peptide segments from the amyloid core of the Sup35 prion protein (27–30), Zn²⁺-NNQQNY, Cd²⁺-NNQQNY, and GNNQQNY, using MicroED (Fig. 1). Some of these had been previously determined by X-ray crystallography (27–31). We chose these nanocrystals to assess the feasibility of experimental phasing by isomorphous replacement using MicroED. Because these nanocrystals diffract to atomic resolution (Fig. 1), we also chose to explore structure determination by direct methods (27). By using MicroED, resolution was significantly improved for all structures over previous X-ray studies, from 1.3 to 1.0 Å for Zn²⁺-NNQQNY (PDB ID code 1YJO), from 1.8 to 1.1 Å for GNNQQNY form 1 (PDB ID code 1YJP), and from 2.0 to 1.05 Å for GNNQQNY form 2 (PDB ID code 2OMM).

Fig. 1.

Atomic resolution electron diffraction from amyloid nanocrystals. Diffraction images of Zn²⁺-NNQQNY (A), Cd²⁺-NNQQNY (B), GNNQQNY-P2₁ (C), and GNNQQNY-P2₁2₁2₁ (D). A cross indicates the beam position, rings indicate resolution ranges, and arrows point to high-resolution reflections. Insets show images of crystals (indicated by black arrows) from which the high-resolution diffraction patterns were obtained. (Scale bars, 2 μm.)

To limit the radiation damage experienced by the crystals, we measured continuous rotation MicroED data at a dose rate <0.01e⁻ per square angstrom per second. From the illuminated area and size of our crystals, we estimate that, on average, ∼170 × 4,100 × 170 unit cells are illuminated in our experiments. Each frame of the diffraction movie represents a 0.6° wedge of reciprocal space collected during a 2-s exposure. Full datasets were acquired in minutes without exceeding a total accumulated dose of 5e⁻ per square angstrom and processed by X-ray crystallography software to 1.0-Å resolution (Table 1). Multiple datasets were merged to achieve adequate completeness for each of the segments, at high resolution. In the case of GNNQQNY, a single crystal belonging to a different space group, P2₁2₁2₁ instead of P2₁ (27), produced high-resolution data with 77.6% completeness at 1.0 Å (Table 1).

Table 1.

Crystallographic structure determination

Crystal	Zn2+-NNQQNY	Cd2+-NNQQNY	GNNQQNY-P21	GNNQQNY-P212121
Data collection
Radiation source	Electron FEG	Electron FEG	Electron FEG	Electron FEG
Dose upper limit, e−/ Å2	5	5	5	5
Space group	P21	P21	P21	P212121
Cell dimensions
a,b,c, Å	21.5, 4.9, 23.9	22.1, 4.9, 23.5	22.9, 4.9, 24.2	23.2, 4.9, 40.5
α,β,γ, °	90, 104.0, 90	90, 104.3, 90	90, 107.8, 90	90, 90, 90
Resolution limit, Å	1.00 (1.06–1.00)	1.00 (1.05–1.00)	1.10 (1.16–1.10)	1.05 (1.11–1.05)
Wavelength, Å	0.0251	0.0251	0.0251	0.0251
No. of crystals merged	6	4	4	1
Rmerge	0.151 (0.245)	0.180 (0.282)	0.265 (0.450)	0.199 (0.586)
Rr.i.m.	0.163 (0.280)	0.203 (0.363)	0.286 (0.482)	0.230 (0.669)
Rp.i.m.	0.057 (0.111)	0.087 (0.181)	0.139 (0.223)	0.109 (0.305)
I/σI	10.2 (6.6)	7.3 (3.7)	4.6 (3.0)	4.2 (1.8)
CC1/2, %	98.5 (90.6)	96.6 (53.9)	98.4 (88.4)	98.5 (69.3)
Completeness, %	82.6 (55.3)	84.5 (66.0)	94.8 (96.0)	78.6 (79.3)
Multiplicity	7.1 (5.1)	4.6 (3.3)	6.6 (7.2)	3.7 (3.7)
Unique reflections	2,360 (202)	2,542 (257)	2,219 (326)	1,837 (257)
Refinement
Resolution range, Å	22–1.0	22–1.0	23–1.1	20–1.05
No. of reflections (work)	2,124	2,308	1,997	1,653
Rwork	0.156	0.220	0.187	0.177
Rfree	0.194	0.242	0.224	0.186
CCwork	0.955	0.922	0.954	0.966
CCfree	0.912	0.934	0.947	0.979
No. of atoms (incl. hydrogen)	111	113	114	113
Protein	97	98	107	107
Water	6	7	7	6
Cation	1	1	0	0
Acetate	7	7	0	0
B factors, Å2
Protein	4.0	4.9	4.5	4.2
Water	12.9	16.0	14.5	14.7
Cation	3.7	11.3	n/a	n/a
Acetate	4.1	17.2	n/a	n/a
Wilson B, Å2	3.2	3.4	6.1	5.7
Rms deviations
Bond lengths, Å	0.020	0.021	0.019	0.017
Bond angles, °	1.5	1.7	1.3	1.6

Numbers reported in parentheses correspond to values in the highest-resolution shell. incl., including; n/a, not applicable.

Strong anomalous signals are not expected for electron diffraction because the energy of the electron beam is far from any known resonance phenomenon in the elements composing the crystal. Indeed, no significant anomalous signal was detected in our datasets, as evidenced by the poor correlation in Friedel differences between randomly chosen half datasets, at <30% in all cases (Table S1). In contrast, anomalous signals are routinely used in X-ray diffraction experiments to assist in phase determination (3, 4) and are enhanced by tuning the X-ray energy to an absorbance maximum specific to a particular element in the crystal. As a case in point, an anomalous signal sufficient for phasing was reported from Zn²⁺-NNQQNY crystals using a microfocus synchrotron X-ray source (27). As expected, the anomalous correlations from this experiment are significantly higher than for MicroED (Table S1). A detectable anomalous signal has been reported from electron diffraction experiments in the gas phase and attributed to the modification of the potential field by the presence of the incident electron (32). Evidently, the magnitude of this effect (second Born approximation) proved too small to measure in our experiments.

Table S1.

Anomalous correlation coefficients (CC_ano) comparing anomalous differences between randomly selected half-datasets

Resolution	CCano, %
	X-ray	Electron
	Zn2+-NNQQNY	Zn2+-NNQQNY	Cd2+-NNQQNY	GNNQQNY-P21	GNNQQNY-P212121
20.0–2.60	55	13	23	−34	−5
2.60–2.00	27	10	19	−10	−2
2.00–1.70	32	9	15	−36	−10
1.70–1.50	32	26	11	−20	1
1.50–1.35	20	−1	5	−29	4
1.35–1.25	—	15	2	−36	−4
1.25–1.15	—	7	1	−15	−7
1.15–1.10	—	6	−12	−14	−11

The low correlation values indicate that there is no significant anomalous signal from any of the crystals. X-ray data for Zn²⁺-NNQQNY originates from Nelson et al. (27). Data not measured are indicated by a dash.

The data collected by continuous rotation MicroED and processed by X-ray crystallography software show nearly kinematic scattering devoid of dynamical scattering artifacts. Reflections forbidden by symmetry are overall absent or present at <8% of the measured intensities for their allowed counterparts on average (Table S2). Furthermore, comparisons of reflections related by Friedel symmetry (R_Friedel) and non-Friedel symmetry (R_non-Friedel) gave no strong indication of dynamical scattering (Table S3). We found the differences between R_Friedel and R_non-Friedel are small: at <1% in many datasets (Table S3).

Table S2.

Measured intensities for [0, n*K, 0] reflections in space group P2₁

Allowed reflections are colored in blue.

Table S3.

Comparisons of R_Friedel and R_non-Friedel offer insight into the magnitude of dynamical scattering

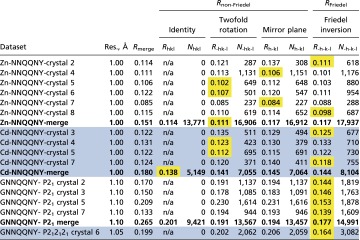Statistics for composite datasets (merges of multiple crystals) are shown in bold. Component datasets (entirely from a single crystal) are shown in regular font. Alternate white and blue shading is used to group together crystals belonging to the same project, and distinguish the four different projects. A conventional R_merge was calculated by using all reciprocal space symmetry operators appropriate for the space group and R_hkl, R_-hk-l, R_h-kl, and R_-h-k-l were calculated by using individual symmetry operators. The contribution of dynamical effects to violations of Friedel symmetry (R_Friedel or R_-h-k-l) has been reported as negligible in electron diffraction experiments with bacteriorhodopsin (24, 43), presumably because electron beam paths are equivalent for Friedel mates (i.e., I_hkl and I_–h-k-l originate from opposite sides of the same Bragg plane). In contrast, dynamical effects can potentially contribute to violations of non-Friedel symmetry (R_non-Friedel) because electron beam paths for non-Friedel symmetry-related reflections (e.g., I_hkl and I_–hk-l) do not share the same path. Comparison of R_Friedel and R_non-Friedel therefore offer an estimate of the magnitude of dynamical scattering. If dynamical scattering is strong, then we would expect R_Friedel << R_non-Friedel. Instead, we find R_Friedel ∼ R_non-Friedel. The symmetry operator that produces the lowest R factor is highlighted with a yellow background. In the cases where R_Friedel < R_non-Friedel, the difference is small in comparison with the increase in R_merge incurred by merging together crystals. Hence, dynamical scattering effects on R_merge appear to be similar or less than typical levels of crystal nonisomorphism. Reflections containing an index of zero were not included in R_sym calculations because they are related by multiple symmetry operators. N_sym reports the number of pairs of reflections compared. The merging R factors were calculated by using the following equation: Σ_hkl Σ_j |<I_hkl> − I_hkl,j|/ Σ_hkl Σ_j I_hkl,j. For R_hkl, R_-hk-l, R_h-kl, and R_-h-k-l, j ranges from 1 to 2 only.

We evaluated our hypothesis that intensities measured at atomic resolution by MicroED from all four peptide nanocrystals are sufficient for structure determination using ab initio structure determination methods. We executed the direct-methods protocol with standard parameters using the SHELXD software package (SI Methods) (12). Direct methods solutions were obtained for all four datasets: Zn²⁺-NNQQNY, Cd²⁺-NNQQNY, GNNQQNY-P2₁ and GNNQQNY-P2₁2₁2₁ (Fig. S1). In each case, the ensembles of atoms generated by SHELXD were correctly assigned and interpretable as peptide segments in the amyloid state (Fig. 2 and Table S4). Their structures were refined (Fig. 2) to fit the diffraction measurements (Methods). Each refined structure included hydrogen atoms that fit well into high-resolution density maps (Fig. S2 and Table S5). Refined structures also showed strong densities for the coordinated Zn²⁺ and Cd²⁺ ions, which scaled in proportion to their atomic numbers.

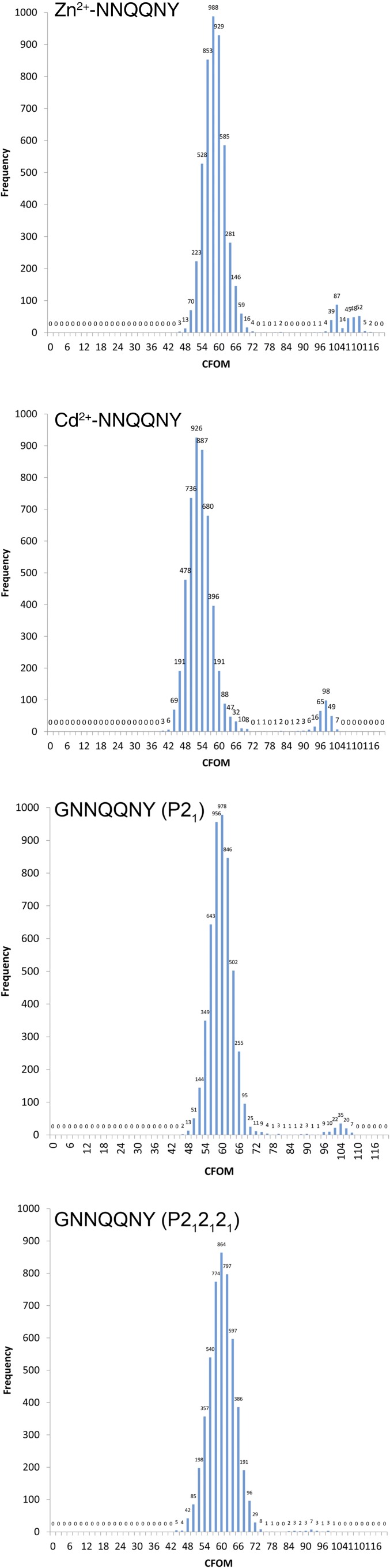
Fig. S1.

Histograms of combined figure of merit (CFOM) scores indicate the frequency of obtaining correct solutions by direct methods using ShelxD. Each histogram indicates the distribution of 5,000 independent CFOM scores obtained for each of the four sup35 structures. Correct solutions have CFOM scores > 80. A clear separation between incorrect and correct structures is indicated by the bimodal distributions of CFOM scores. The smaller of the two peaks in the distribution correspond to correct solutions (higher CFOMs). The two metal-containing structures have a higher frequency of obtaining a correct structure compared with the two non-metal-containing structures. The presence of the metal may be a factor in facilitating a correct direct methods solution. We also note that the two structures that contain metals correspond to higher-resolution (higher-quality) datasets, which also facilitate a correct direct-methods solution.

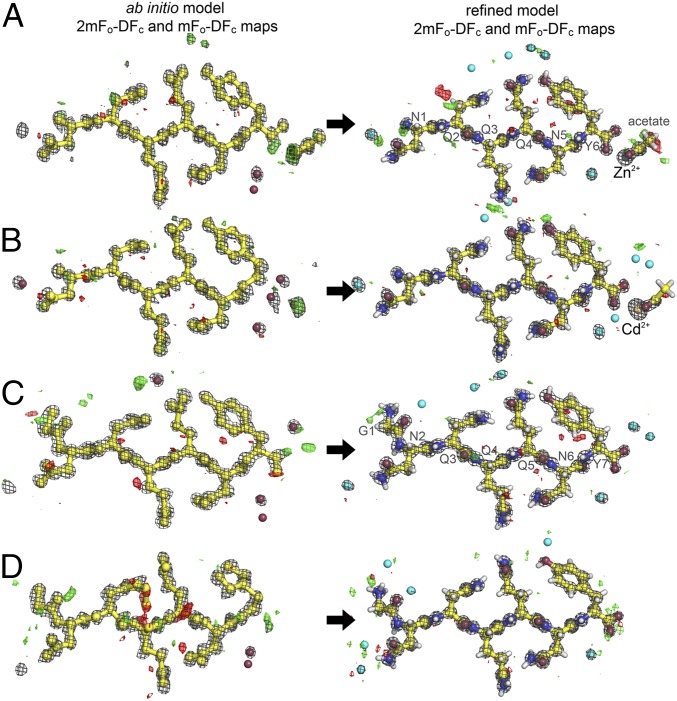
Fig. 2.

Density maps from ab initio and final refined model. Structures of Zn²⁺-NNQQNY (A), Cd²⁺-NNQQNY (B), GNNQQNY-P2₁ (C), and GNNQQNY-P2₁2₁2₁ (D) are shown. Note that a majority of the peptide atoms were correctly placed by direct methods. The σ_A-weighted 2mF_o − DF_c maps (gray) are contoured at 1.8 σ. The σ_A-weighted mF_o − DF_c maps are contoured at +3.0 σ (green) and −3.0 (red) σ. Modeled water molecules are depicted as cyan-colored spheres.

Table S4.

Ab initio structure determination statistics

Crystal	Zn-NNQQNY	Cd-NNQQNY	GNNQQNY-P21	GNNQQNY-P212121
Best CFOM	92.8	84.3	90.8	89.4
Best FCC	63.3	61.0	62.1	64.8
Peptide atoms (excluding hydrogen)	55	55	59	59
Peptide atoms correctly placed (excluding hydrogen)	54	54	58	54

Table shows CFOM, final correlation coefficient (FCC), number of atoms identified in the ab initio solution by SHELXD, number of atoms placed correctly, and number of atoms in the final map.

Fig. S2.

Hydrogen atom positions are revealed by a σ_A weighted F_o − F_c map. (A) The residual map is contoured at +3.0 σ (green) and −3.0 σ (red). The map was calculated by using phases from a model of GNNQQNY (P2₁2₁2₁), which had no hydrogens included, nor had any hydrogens been introduced at any point leading to this model. (B) GNNQQNY with hydrogen atoms (black) modeled in riding positions. All of these peaks (20) are within 1.0 Å of the geometrically positioned hydrogen atoms and are labeled by the hydrogen atom. These account for 42% of the total hydrogen atoms present. No hydrogen atoms were detected on water molecules (cyan spheres).

Table S5.

Number of hydrogen atoms verified by residual peaks in a simulated omit hydrogen map

Structure	Peptide hydrogens		Water hydrogens
	Located	Possible	Located	Possible
Zn2+-NNQQNY	16	45	0	12
Cd2+-NNQQNY	9	45	0	14
GNNQQNY- P21	16	48	0	14
GNNQQNY- P212121	19	48	0	12

Peaks must be 3σ or greater in height and <1.0 Å distant from refined hydrogen position to be counted as “located.” Simulated annealing temperature was 5,000 K (44).

SI Methods

Sample Input Parameters for Ab Initio Structure Determination Using SHELXD.

• TITL Zn-NNQQNY in P2(1)

• CELL 0.0251 21.4800 4.9500 23.8700 90.000 103.952 90.000

• ZERR 0.001 0.0083 0.0008 0.0082 0.000 0.100 0.000

• LATT -1

• SYMM -X, 0.5+Y, -Z

• SFAC C H N O Zn

• UNIT 31 45 11 13 1

• NTRY 5000

• FIND 75

• PLOP 50 80 120 160 160

• HKLF 4

• END

Search Parameters for Identification of X-Ray Structures in PDB with Resolution Better than or Equal to 1.1 Å.

The pdbU server at the University of California, Los Angeles (services.mbi.ucla.edu/pdbU) provides a method of searching the Research Collaboratory for Structural Bioinformatics (118,763 structures; last updated April 13, 2016) for structures matching specific criteria. We used this server to filter all PDB entries by resolution cutoff and X-ray technique. The server provides the number of current entries that satisfy our search criteria and lists the details of each entry.

Discussion

The structures of Zn²⁺-NNQQNY, Cd²⁺-NNQQNY, GNNQQNY-P2₁, and GNNQQNY-P2₁2₁2₁ demonstrate that MicroED can satisfy the stringent requirements for ab initio phasing of macromolecules—specifically, the measurement of accurate high-resolution intensities. Several experimental challenges were overcome to achieve this. We minimized the total electron dose delivered to a crystal to maintain its high-resolution diffraction. Continuous rotation MicroED data collection was used to minimize dynamical scattering. We collected diffraction data from multiple crystals in varied orientations to fill the reciprocal space. We selected crystals for merging based on isomorphism; nonisomorphism can limit the accuracy of the final intensities. In one case, we determined an ab initio structure from a single nanocrystal in space group P2₁2₁2₁.

Our structures are of small macromolecules, but the principles that govern our direct methods approach are applicable to larger proteins. Currently, 1,540 structures present in the PDB diffract to better than 1.1 Å (SI Methods). An unknown number of proteins like these could be future targets for ab initio phasing by MicroED. Phasing by direct methods is computationally more challenging for larger macromolecules, but the technique has already been widely demonstrated on structures that range in complexity from a few atoms to several thousand (7, 10). Ultimately, crystal size, number of unit cells, and crystalline order can all limit high-resolution diffraction to a range below that required by direct methods. We show here that the resolution limit for successful direct methods phasing is the same for MicroED and X-ray diffraction––better than 1.2-Å resolution (8). Indeed, success of direct methods using various resolution cutoffs on our GNNQQNY-P2₁ data showed that, of 5,000 trials, we found 126 successes at 1.1 Å, 2 successes at 1.15 Å, and 0 successes at 1.2 Å. Thus, a more general approach for phasing of MicroED data may be required for routine de novo phasing of macromolecular structures from submicrometer crystals.

Electrons, because of their strong interaction with matter, can potentially produce high-resolution diffraction patterns from tiny 3D crystals. Therefore, MicroED is well suited for answering questions that require high-resolution diffraction from dose-sensitive biological macromolecular samples studied under cryogenic conditions. The atomic arrangements solved by direct methods present a unique opportunity for further improvement of our current estimates of electron scattering factors. Our atomic structures include hydrogen atoms, which play a central role in many biochemical processes; knowing their positions has provided important insights into catalytic mechanisms (33, 34) and greatly aids rational drug design (35). Lastly, by using direct methods, MicroED can also provide ab initio solutions for small-molecule organic compounds, such as rare pharmaceutical polymorphs (36) and designer peptoids (37) that challenge other means of investigation.

Conclusion

We present four ab initio structures determined by cryo-EM. At 1-Å resolution, these are the highest-resolution cryo-EM structures to date, determined by either imaging or diffraction. Our proof-of-principle determination of these structures speaks to the broader potential of applying ab initio phasing to MicroED. Future targets include new structures yet to be solved by traditional crystallographic means from well-ordered nanocrystals that may diffract to high resolution, but are presently overlooked because of their small size.

Methods

Preparation of Peptide Nanocrystals.

Lyophilized, synthetic GNNQQNY and NNQQNY peptides were purchased from Genscript and dissolved in ultrapure water. GNNQQNY was prepared at a concentration of 10 mg/mL, and NNQQNY was prepared at a concentration of 30 mg/mL The dissolved peptides were then filtered by using a 0.22-μm cutoff filter.

Crystals of Zn²⁺- and Cd²⁺-NNQQNY were grown by hanging-drop vapor diffusion at ∼20 °C. The reservoir solution contained 100 mM Hepes (pH 7.0) and 1 M sodium acetate (pH not adjusted). Drops were prepared by pipetting 5 μL of peptide solution, 4 μL of reservoir solution, and 1 μL of 0.1 M ZnSO₄ or CdSO₄ onto a glass coverslip. Crystals of Zn²⁺-NNQQNY grew within a day.

Crystals of Zn²⁺-NNQQNY were used to seed growth of GNNQQNY crystals to ensure isomorphism (27). Crystals of GNNQQNY were grown in batch at ∼20 °C in ultrapure water.

Collection of MicroED Data by Continuous Rotation.

MicroED data from Zn²⁺-, Cd²⁺-NNQQNY, and GNNQQNY nanocrystals were collected in an identical way, and similar to what has been described for other nanocrystals (18, 21, 38). Briefly, for each of these samples, nanocrystals were harvested, and a single crystal suspension was generated by mixing of crystal-containing solutions. A small amount (∼2 μL) of the crystal suspension was placed on quantifoil EM grids (R2/2, 300#; EMS). Grids were blotted and plunge-frozen into liquid ethane by using a Vitrobot Mark IV (FEI). Frozen grids were then transferred into liquid nitrogen for storage and later imaging. Frozen hydrated grids were placed in a cryo-TEM (transmission electron microscope) Gatan 626 cryo-holder for imaging and diffraction.

Diffraction patterns and crystal images were collected by using a FEI Tecnai F20 transmission cryo-electron microscope equipped with a field emission electron gun operating at 200 keV and used in diffraction mode. All data were collected by using a bottom-mount TVIPS TemCam-F416 CMOS camera with a sensor size of 4,096 × 4,096 pixels, each 15.6 × 15.6 μm. Diffraction patterns were recorded by operating the detector in rolling shutter mode with 2 × 2-pixel binning, producing a final image 2,048 × 2,048 pixels in size. Individual image frames were taken with exposure times of 2 s per image, by using a selected area aperture with an illuminating spot size of ∼1 μm. This geometry equates to an electron dose rate of <0.01 e⁻ per square angstrom per second. During each exposure, crystals were continuously rotated within the beam at a rate of 0.3° per second, corresponding to a 0.6° wedge of data per frame. Diffraction data were collected from several crystals, each oriented differently with respect to the rotation axis. These datasets each spanned wedges of reciprocal space ranging from 50° to 80°.

We estimate that there are ∼1.0 × 10⁸ unit cells illuminated on average per crystal, per dataset. This value was obtained by approximating the crystal shape as a cylindrical rod with a 200-nm radius and length limited by the 2-μm aperture diameter. Thus, the illuminated volume of the crystal is the volume of a cylinder, πr²h = π × (200 nm)² × (2,000 nm) = 2.5 × 10⁸ nm³. The unit cell volume for the GNNQQNY crystal is 2.29 nm × 0.49 nm × 2.42 nm × sin(104°) = 2.4 nm³. The number of unit cells illuminated by the beam is simply the ratio of the illuminated volume of the crystal to the unit cell volume; this ratio is ∼1.0 × 10⁸ unit cells. This value corresponds approximately to 170 × 4,100 × 170 unit cells. By comparison, the illuminated volume in the original synchrotron X-ray dataset reported in 2005 was ∼16 times greater (27), but did not yield as high resolution (1.8 vs. 1.1 Å).

We did not find it beneficial to illuminate a larger area because any gain in diffracting intensity from a greater volume of diffracting unit cells is offset by the inclusion of background regions and potentially other crystal fragments that would pose a challenge for indexing and integration of measured reflections.

MicroED Data Processing.

Diffraction images were collected as TVIPS movies and converted to SMV crystallographic format as described (18). These images were processed with both XDS/XSCALE (39) and Denzo/Scalepack (40). These programs were primarily developed for X-ray crystallography, but can be adapted for indexing and integration of MicroED data. The two programs yielded comparable statistics in each of the four crystal projects. We chose the Denzo/Scalepack statistics for Zn²⁺- and Cd²⁺-NNQQNY datasets, and XDS/XSCALE for the GNNQQNY in space group P2₁ and P2₁2₁2₁. Indexing and merging statistics are presented in Table 1.

Ab Initio Structure Determination and Refinement.

The SHELX macromolecular structure determination suite was used for phasing the measured intensities (12). The input parameters for the phasing trials by SHELXD are provided in the sample input script (SI Methods). Results for ab initio structure determination using direct methods protocols by SHELXD are presented in Table S1. Refinement was carried out with electron scattering form factors using the program Refmac (41) starting from the atomic coordinates determined by the direct-methods protocol. We used atomic form factors calculated using the electron’s rest mass. These values reported in the International Tables of Crystallography (volume C, table 4.3.1.1) originate from Doyle and Turner (42). The relativistic correction for 200-keV electrons is reported in table 4.3.2.1 as a scaling factor of 1.39138. Application of this correction to the refinement of GNNQQNY-P2₁ produced only insignificant differences. Comparing coordinates refined with and without the correction revealed an rmsd of 0.002 Å over 107 atom pairs. Average B factors differed by only 0.001 Ų. Refinement and structure validation statistics are presented in Table 1.