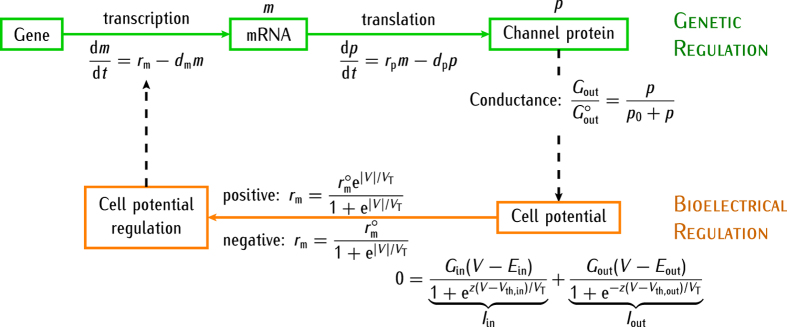
Figure 1. Scheme illustrating the positive and negative feedback scenarios between the genetic and bioelectrical descriptions at the single-cell level.

The model equations for the time (t)-dependent coupling between the genetic and bioelectric regulations are also shown. The dashed arrows show the feedback mechanism between the potential-dependent production of the protein forming the outward-rectifying ion channel and the cell potential modulation due to this channel conductance. The transcription (r_m) and translation (r_p) rate constants together with their corresponding degradation rate constants d_m and d_p lead to the steady-state mRNA and protein concentrations m = r_m/d_m and p = r_pm/d_p = r_pr_m/(d_pd_m), respectively. For the sake of simplicity, the translation rate constant r_p and the degradation rate constants d_mand d_p are assumed to be independent of the potential³⁸,³⁹,⁴⁰. On the contrary, the transcription rate r_m(V) depends on the cell potential V and can be increased (positive regulation) or decreased (negative regulation) with respect to the zero-voltage value 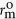according to the absolute value |V|. The potential V is determined by the equation of zero total current through the membrane²⁹, I_in + I_out = 0, where I_in and I_out are the electrical currents through the inward- and outward-rectifying channels¹⁹, respectively. The channel equilibrium potentials are fixed to E_out = 0 mV and E_in = −60 mV and the threshold potentials are V_th,in = V_th,out = −27 mV. The number of effective charges involved in gating²⁹ is assumed to be z = 3 and the thermal potential is V_T = RT/F = 27 mV at 310 K, where R is the gas constant, T is the temperature, and F is the Faraday constant.